6/7 論文紹介資料

1. Salimans, T., Kingma, D. P., & Welling, M.
Proceedings of The 32nd International Conference on Machine Learning,
pp. 1218–1226, 2015 (ICML 2015)
Markov Chain Monte Carlo and
Variational Inference: Bridging the Gap
Presenter : S5lab. Shuuji Mihara

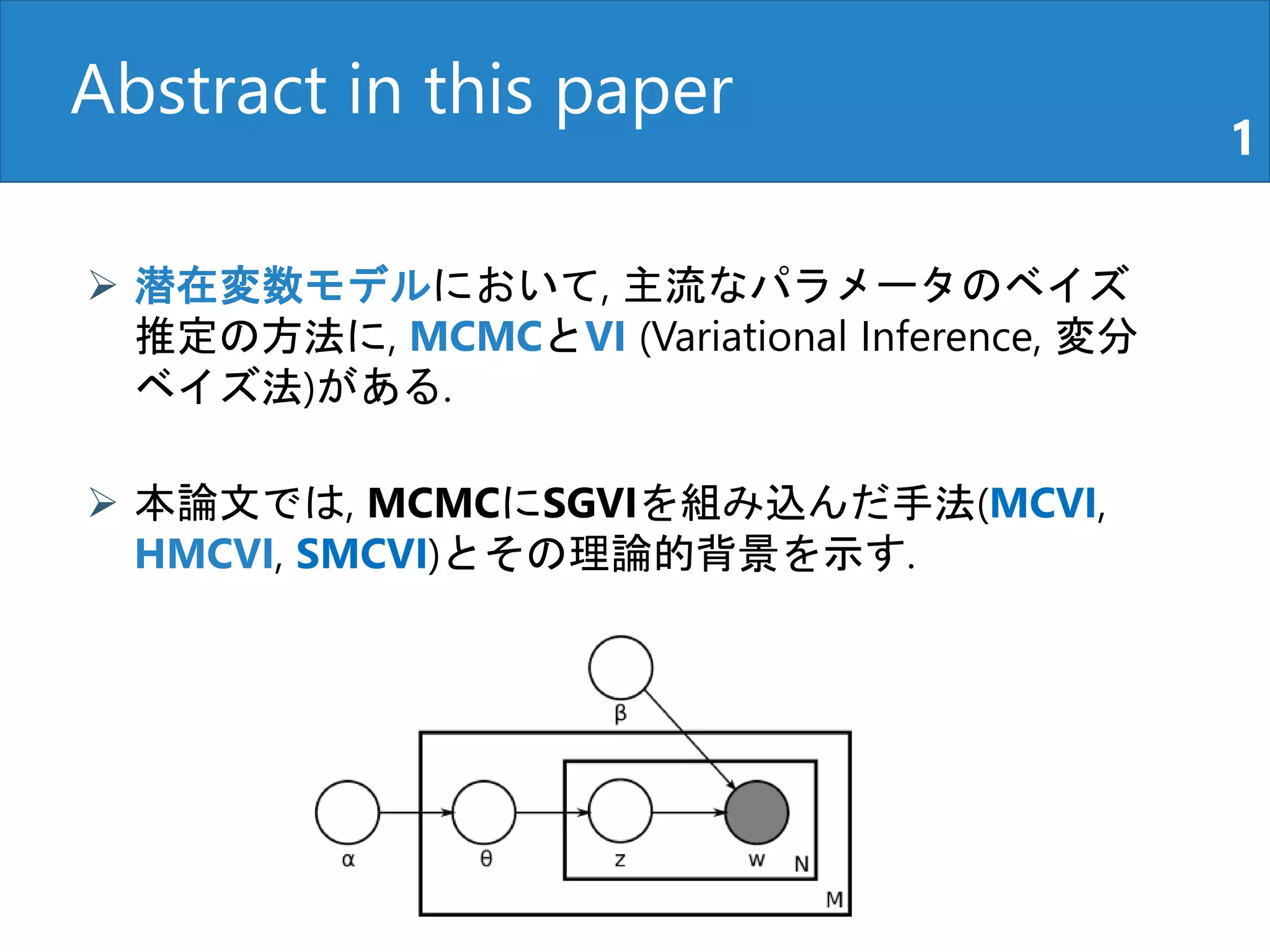
2. Abstract in this paper
1
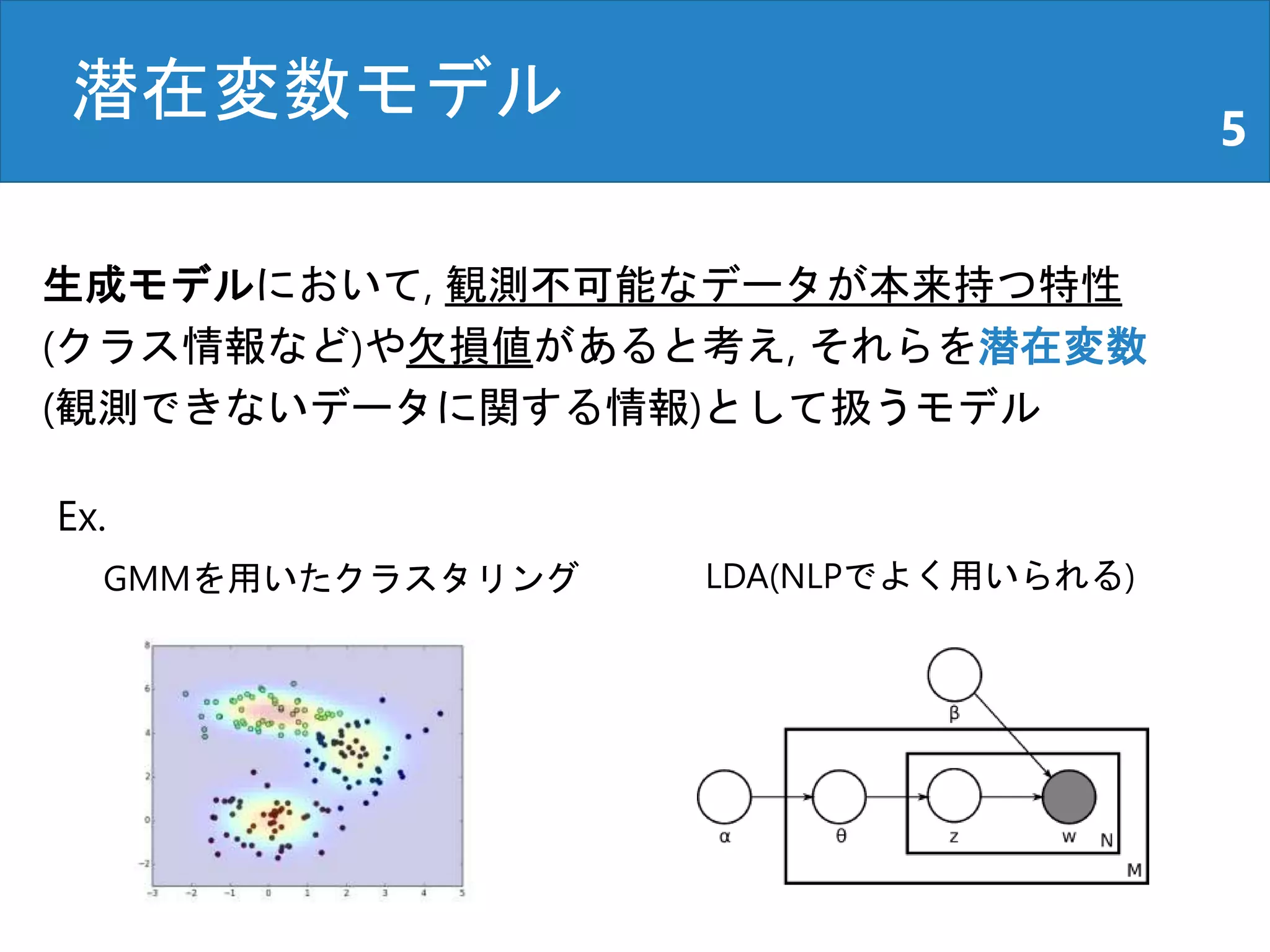
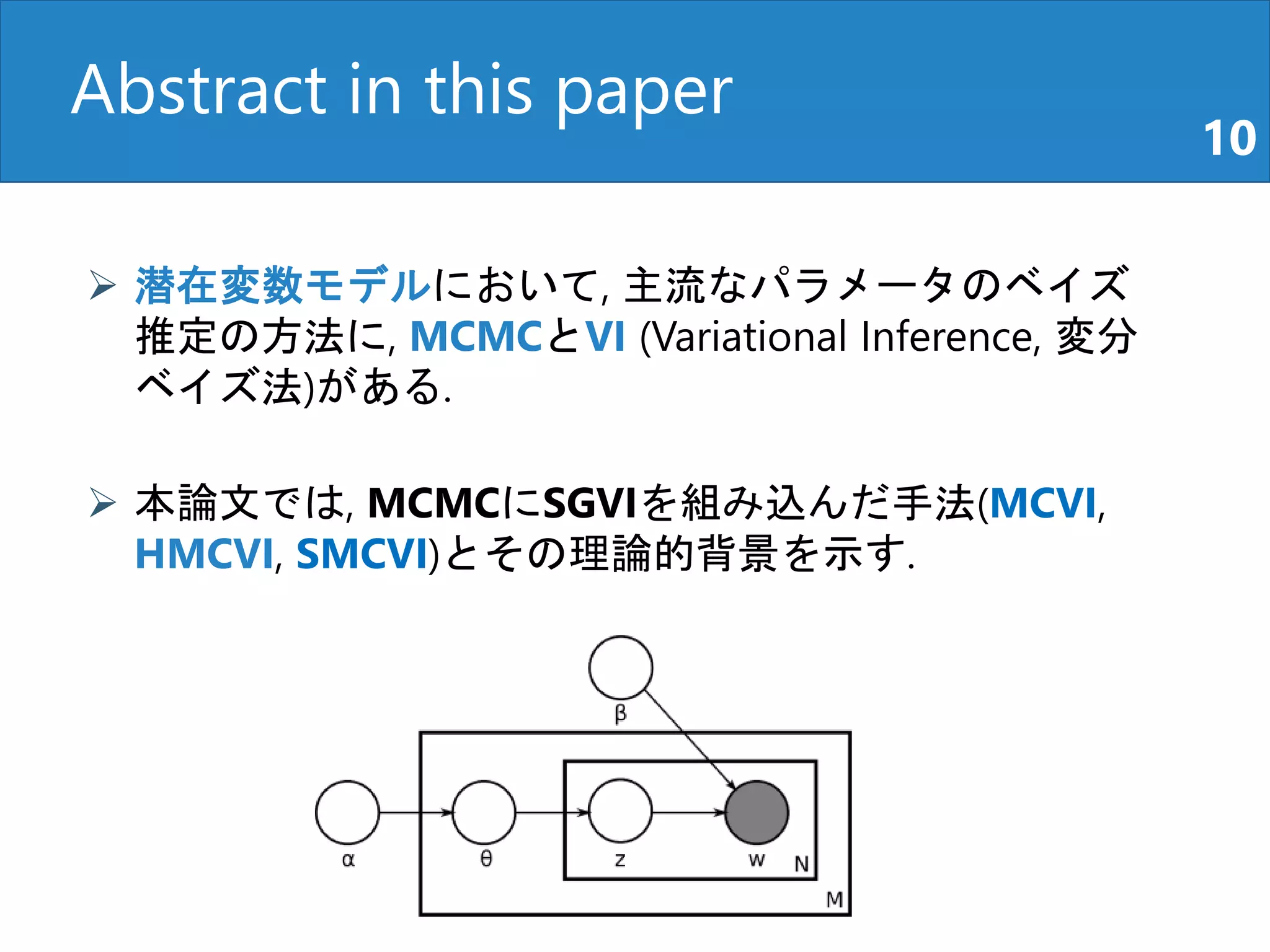
 潜在変数モデルにおいて, 主流なパラメータのベイズ
推定の方法に, MCMCとVI (Variational Inference, 変分
ベイズ法)がある.
 本論文では, MCMCにSGVIを組み込んだ手法(MCVI,
HMCVI, SMCVI)とその理論的背景を示す.

3. Table of Contents 2
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review
論文ではHMC(ハミルトニアンモンテカルロ法)についても言及がありますが,
前提知識が多いため今回は簡単にしか触れません
※

4. Table of Contents 3
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review

5. 生成モデル 4
観測データは未知の真の確率分布から生起していると考え,
その確率分布を推定することでデータの振る舞いを分析す
る考え方
Ex. サイコロ
観測データ
𝑋 = {1,5,4,3,2, … }
真の分布
𝑝(𝑥)
𝑝 𝑥 : すべての目が
1/6の確率で出る?

6. 潜在変数モデル 5
生成モデルにおいて, 観測不可能なデータが本来持つ特性
(クラス情報など)や欠損値があると考え, それらを潜在変数
(観測できないデータに関する情報)として扱うモデル
Ex.
LDA(NLPでよく用いられる)GMMを用いたクラスタリング

7. ベイズ推定 6
推定対象をベイズの定理を用いて分布推定する方法の
総称?(↔点推定(最尤推定))
𝜃 𝜃
最尤推定
(点推定)
ベイズ推定
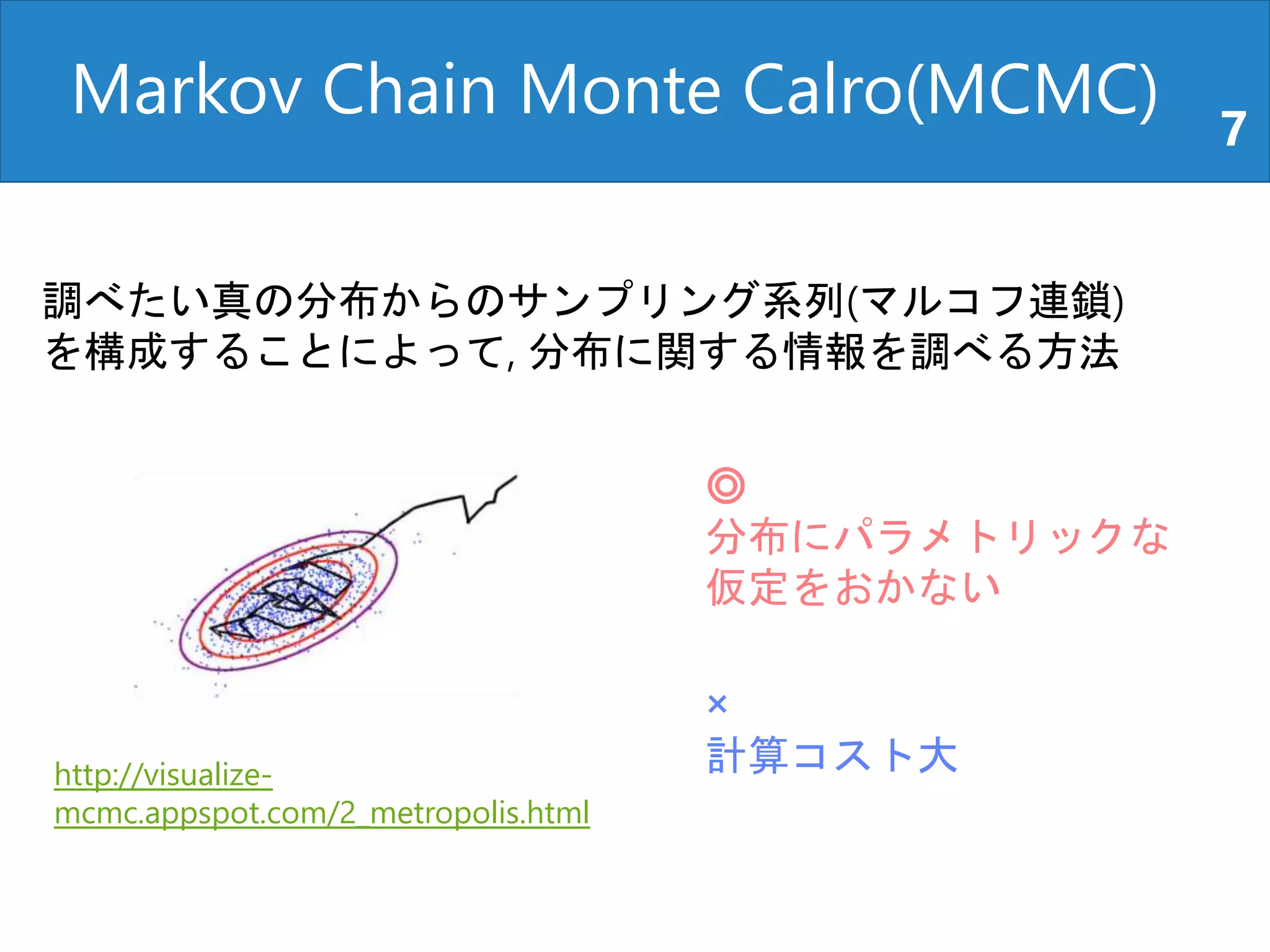
(区間推定)

8. Markov Chain Monte Calro(MCMC) 7
調べたい真の分布からのサンプリング系列(マルコフ連鎖)
を構成することによって, 分布に関する情報を調べる方法
http://visualize-
mcmc.appspot.com/2_metropolis.html
◎
分布にパラメトリックな
仮定をおかない
×
計算コスト大

9. Variational Inference 8
調べたい真の分布に対してパラメトリックな仮定をおき,
一部のパラメータ群の独立性を仮定した近似事後確率を
KL情報量の最小化(変分下限(ELBO)の最大化)により, 解析的に計
算する.
𝐿 = log 𝑝(𝑥) − 𝐾𝐿(𝑞 𝜃 𝑧 𝑥 || 𝑝(𝑧|𝑥))
最大化 最小化
◎
大規模なモデルでも
比較的計算が早い
×
事前に解析的な手計算
が必要
= 𝐸 𝑞 𝜃(𝑧|𝑥)[log 𝑝 𝑥, 𝑧 − log 𝑞 𝜃 (𝑧|𝑥)]
(1), (2)式

10. 事後確率の計算に近似を導入し, 計算量を減らす.
計算式が解析的に導け, 計算コストが少ない,
しかし, 精度は損なわれる.
理論上, 任意の精度での計算が可能. しかし計算コスト大
MCMCとVI 9
大抵の計算問題では正確さと計算量はトレードオフ
MCMC(マルコフ連鎖モンテカルロ法)
VI(Variational Bayes, 変分ベイズ法)
大規模問題への適用が困難!
本論文ではこの2つの手法を融合させる

11. Abstract in this paper
10
 潜在変数モデルにおいて, 主流なパラメータのベイズ
推定の方法に, MCMCとVI (Variational Inference, 変分
ベイズ法)がある.
 本論文では, MCMCにSGVIを組み込んだ手法(MCVI,
HMCVI, SMCVI)とその理論的背景を示す.

12. Table of Contents 11
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review

13. What’s difficult in MCMC? 12
MCMC(MH法)の難しい点
• 提案分布をどのように構成するか
• 何回サンプリングを繰り返せば精度のいい
近似事後分布が得られるかわからない

14. What’s difficult in MCMC? 13
MCMC(MH法)の難しい点
• 提案分布をどのように構成するか
• 何回サンプリングを繰り返せば精度のいい
近似事後分布が得られるかわからない
提案手法で解決

15. The central idea of this paper(1) 14
MCMCで得られる事後分布はマルコフ連鎖なので
以下のように分解できる.
𝑞 𝑧 𝑥 = 𝑞(𝑧0|𝑥)
𝑡=1
𝑇
𝑞(𝑧𝑡|𝑧𝑡−1, 𝑥)
補助変数の集合 𝑦 = 𝑧0, 𝑧1, … , 𝑧𝑡−1
および補助分布 𝑟(𝑦|𝑥, 𝑧 𝑇)
を導入することで, (2)式で見た補助変分下限(変分下限の下限)
が(3)式のように求められる

16. The central idea of this paper(2) 15
𝐿 ≥ 𝐿 𝑎𝑢𝑥 = 𝐸 𝑞(𝑦,𝑧 𝑇|𝑥) [log 𝑝 𝑥, 𝑧 𝑇 𝑟 𝑦 𝑥, 𝑧 𝑇 − log 𝑞(𝑦, 𝑧 𝑇|𝑥)]
= 𝐿 − 𝐸 𝑞(𝑧 𝑇|𝑥)
{𝐷 𝐾𝐿[𝑞 𝑦 𝑧 𝑇, 𝑥 ||𝑟(𝑦 |𝑧 𝑇, 𝑥)]}
(3)式

17. The central idea of this paper(3) 16
さらに補助分布𝑟にマルコフ性を仮定することで,
以下の補助変分下限の逐次更新式を得る.((4)式)
𝐿 𝑎𝑢𝑥
= 𝐸 𝑞[log 𝑝 𝑥, 𝑧 𝑇 − log 𝑞 𝑧0 𝑥
+
𝑡=1
𝑇
log[𝑟𝑡(𝑧𝑡−1|𝑥, 𝑧𝑡)/𝑞𝑡(𝑧𝑡|𝑥, 𝑧𝑡−1)]]
MCMCの各ステップで変分下限の推定量が得られる
Algorithm1

18. Table of Contents 17
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review

19. Algorithm 1 18

20. Table of Contents 19
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review

21. 20
Stochastic Gradient Variational Bayes
Reparameterization Trick:
𝑞 𝜙 𝑤 から直接𝑤をサンプリングする代わりに、
𝑤 = 𝑓 𝜀, 𝜙 , 𝜖~𝑝 𝜖 が𝑞 𝜙 𝑤 に従うよう𝑓, 𝑝 𝜖 を決める
例)
𝒩 𝜇, 𝜎 からサンプリングする代わりに、
𝑤 = 𝜇 + 𝜎𝜀, 𝜀~𝒩 0,1 とする

22. MCVI概要 21
Algorithm1において提案分布にReparameterization trick
(𝑧𝑡 = 𝑔 𝜃(𝑢 𝑡, 𝑥))を導入することで, 𝐿の推定量を
𝜃の関数として表す.
𝐿の確率的最適化により, 𝜃を計算
＝提案分布のパラメータが決定される

23. Algorithm 2 22

24. Example : bivariate Gaussian 23

25. Hamiltonian Variational Inference 24
State of the art

26. Table of Contents 25
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review

27. SMCVI 26
MCVIは全ステップで変分下限の最適化を行うのに対して,
代わりに各ステップでの変分下限の更新量の期待値
(𝐸 𝑞 log 𝛼 𝑡)の最適化を行い,
各ステップで潜在変数の事後分布を計算する.

28. Algorithm4 27

29. Table of Contents 28
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Review

30. Review 29
• VIをMCMCに組み込む手法を開発し, VIの手法を
MCMCのフレームワークに組み込むことに成功した.
• 数値実験で推定速度の向上を示し, HMCVIでは画像
の生成モデルを推定する問題でState of the artの手
法と遜色ない結果が得られた.

31. Table of Contents 30
1. Introduction
2. MCMC and Auxiliary Variables
3. MCMC lower bound estimate
4. MCVI
5. SMCVI
6. Specification of the Markov chain
7. Review

32. Detailed balance 31
MCMCでは通常, 得られる分布が普遍分布となるよう
以下の詳細釣り合い条件をみたすようにマルコフ連鎖
を構成する.
このときAlgorithm1のlog 𝛼 𝑡の式が以下のように書き換え
られる.