The document provides an overview of the integration of machine learning (ML) into automated reasoning and theorem proving, detailing various approaches and successful projects. It explores the synergy between interactive theorem provers (ITPs) and automated theorem provers (ATPs), emphasizing the role of ML in improving premises and heuristics selection. Several notable projects, such as ML4PG and MASH, showcase the advancements enabled by applying machine learning techniques to enhance proof development and theorem proving efficiency.

1. Introduction Background Different approaches Latest successful projects Conclusion
Machine Learning for Automated Reasoning: An
Overview
Vincenzo Lomonaco
Alma Mater Studiorum - University of Bologna
vincenzo.lomonaco@studio.unibo.it
January 27, 2015
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

2. Introduction Background Different approaches Latest successful projects Conclusion
Index
1 Introduction
2 Background
ITPs and ATPs
Machine learning
3 Different approaches
ML for premises selection
ML for heuristics selection
4 Latest successful projects
ML4PG
MaSh
MaLARea
MaLeCoP
MaLeS
5 Conclusion
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

3. Introduction Background Different approaches Latest successful projects Conclusion
Summary
In recent years, development of interactive and automated theo-
rem provers has led to creation of big data sets of formal mathemat-
ical libraries and varied infrastructures for proofs and software/hardware
verification.
At the same time, machine learning techniques has shown to per-
form well on a large number of tasks in the field of artificial intelli-
gence and Automated Reasoning.
In this talk we cover a number of successful approaches that aim to
exploit this increasing amount of data, learning inductively from
previous proofs.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

4. Introduction Background Different approaches Latest successful projects Conclusion
Introduction I
In Principia Mathematica [18], Whitehead and Russell set out
to show by example that all of mathematics can be derived
from a small set of axioms using an appropriate logical
calculus.
Even though G¨odel later showed that no effectively generated
consistent axiom system can capture all mathematical truth
[6], Principia Mathematica showed that most of normal
mathematics can indeed be catered by a formal system.
With the advent of computers, formal mathematics became a
more realistic proposal
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

5. Introduction Background Different approaches Latest successful projects Conclusion
Introduction II
In the last few decades the exponential raise in computer
power and Computer commodities has lead to an increasing
interest and hope in interactive and automated theorem
proving (ITP and ATP) softwares resumable in the strong
quote by Art Quaife [16] in 1992:
The time will come when such crushers as
Riemann’s hypothesis and Goldbach’s conjecture will
be fair game for automated reasoning programs. For
those of us who arrange to stick around, endless fun
awaits us in the automated development and
eventual enrichment of the corpus of mathematics.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

6. Introduction Background Different approaches Latest successful projects Conclusion
Introduction III
Before the pioneer work of Josef Urban applying first-order
logic ATP methods on large corpus of formal mathematical
proofs (Mizar Mathematical Library also known as MML) in
2003 [22] the field was slowing down.
Then, an increasing number of projects about linking ITP
libraries to ATP emerged and led to a new hope.
Last recent advances in the fields of Artificial Intelligence
(AI) and Machine Learning (ML) are now shaping the way of
thinking about theorem proving and automated reasoning in
general.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

7. Introduction Background Different approaches Latest successful projects Conclusion
Introduction IV
The novel idea
The novel idea is to take statistical inferences about previous proofs
into consideration and merge this kind of inductive reasoning with
the classical deductive reasoning used in ATP and ITP.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

8. Introduction Background Different approaches Latest successful projects Conclusion
Background
In this section we provide a brief background for covering both as-
pects of Machine Learning and Theorem proving.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

9. Introduction Background Different approaches Latest successful projects Conclusion
ITPs and ATPs
ITPs
Interactive theorem provers (ITP), or proof assistants, are
computer programs that support the creation of formal proofs.
Proofs are written in the input language of the ITP, which can
be thought of as being at the intersection between a
programming language, a logic, and a mathematical
typesetting system.
ACL2 [10], Coq [3], HOL4 [21], HOL Light [8], Isabelle [13],
Mizar [7], PVS [15] and Matita [2] are perhaps the most
widely used ITPs.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

10. Introduction Background Different approaches Latest successful projects Conclusion
ITPs and ATPs
ATPs
In contrast to interactive theorem provers, automated
theorem provers (ATPs) work without human interaction.
They take a problem as input, consisting of a set of axioms
and a conjecture, and attempt to deduce the conjecture from
the axioms.
E [19], SPASS [25], Vampire [17], and Z3 [5] are well-known
ATPs for classical first-order logic.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

11. Introduction Background Different approaches Latest successful projects Conclusion
Machine learning
Machine Learning I
Machine learning concerns itself with extracting information
from data [1].The results of a learning algorithm is a
prediction function that takes a new datapoint and returns a
target value.
Features are the input of the prediction function and should
describe the relevant attributes of the datapoint. A datapoint
can have several possible feature representations. Feature
engineering concerns itself with identifying relevant features
[12].
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

12. Introduction Background Different approaches Latest successful projects Conclusion
Machine learning
Machine Learning II
From a mathematical point of view, most machine learning
problems can be reduced to an optimization problem:
Let D ⊆ X × T be a training dataset consisting of datapoints
and their corresponding target value.
Let ϕ : X → Ω be a feature function that maps a datapoint to
its feature representation in the feature space Ω (usually a
subset of Rn for some n ∈ R).
Furthermore, let F ⊆ (Ω → T) be a set of functions that map
features to the target space and s a (convex) score function
s : D × F → R.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

13. Introduction Background Different approaches Latest successful projects Conclusion
Machine learning
Machine Learning III
One possible goal is to find the function f ∈ F that
maximizes the average score over the training set D.
The main differences between various learning algorithms are
the function space F and the score function s they use.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

14. Introduction Background Different approaches Latest successful projects Conclusion
Different approaches I
The AI fields of deductive reasoning and inductive reasoning (rep-
resented by machine learning, data mining, knowledge discovery in
databases, etc.) have so far benefited relatively little from each
other’s progress.
This is an obvious deficiency in comparison with the human mind,
which can both inductively suggest new ideas and problem solu-
tions based on analogy, memory, statistical evidence, etc., and also
confirm, adjust, and even significantly modify these ideas and prob-
lem solutions by deductive reasoning and explanation, based on the
understanding of the world.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

15. Introduction Background Different approaches Latest successful projects Conclusion
Different approaches II
In recent years, a number of different actions and approaches
have been taken in this direction. We can categorize them in two
main branches:
ML for premises selection
ML for heuristics selection
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

16. Introduction Background Different approaches Latest successful projects Conclusion
ML for premises selection
ML for premises selection
Premise selection can be useful as a standalone service for the ITPs
(suggesting relevant lemmas), or in conjunction with ATP methods
that can attempt to find a proof from the relevant premises.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

17. Introduction Background Different approaches Latest successful projects Conclusion
ML for premises selection
Guideline
In the training phase, the learning algorithm is allowed to learn from
the proofs of all previously proved theorems. For all theorems in the
training set, their corresponding dependencies should be ranked as
high as possible. I.e., the score function should optimize the ranks
of the premises that were used in the proof.
To do this all learning algorithms require a set of features as input
data codified as a real vector. Therefore a method is needed to
translate formula trees into real vectors that tries to characterize
the formula.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

18. Introduction Background Different approaches Latest successful projects Conclusion
ML for premises selection
Dependencies graph and Formula Tree examples
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

19. Introduction Background Different approaches Latest successful projects Conclusion
ML for premises selection
Features to use
The symbols that appear in a formula can be seen as its
basic characterization and hence a simple approach is to take
the set of symbols of a formula as its feature set.
The symbols correspond to the node labels in the formula tree.
In addition to the symbols, one can also include as features
the subterms and subformulas of the formula to prove.
Since the formalisms supported by the vast majority of ITP
systems are typed (or sorted) adding the types that appear in
the formula tree as additional features is reasonable.
Adding the feature vectors of some of the last previously
proved theorems to the feature vector of the conjecture, in a
weighted fashion, is a way to add information about the
context.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

20. Introduction Background Different approaches Latest successful projects Conclusion
ML for premises selection
Math point of view
The problem could be seen as a classification problem where for each
premise p ∈ Γ we learn a real-valued classifier function:
Cp(·) := Γ → R (1)
which, given a conjecture c, estimates how useful p is for proving c.
The premises for a conjecture c ∈ Γ are then ranked by the values
of Cp(c).
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

21. Introduction Background Different approaches Latest successful projects Conclusion
ML for heuristics selection
ML for heuristics selection
Automated theorem proving is a search problem. Many different
approaches exist, and most of them have parameters that can be
tuned. Examples of such parameterizations are clause weighting
and selection schemes, term orderings, and sets of inference and
reduction rules used.
A specific choice of parameters defines a search strategy. The
choice of a strategy can often make the difference between finding
a proof in a few milliseconds or not at all.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

22. Introduction Background Different approaches Latest successful projects Conclusion
ML for heuristics selection
Guideline
The strategy selection problem consists of three subproblems:
Finding a good set of preselected strategies .
Defining features Ω which are easy to compute (via a feature
function ϕ , but also expressive enough to distinguish different
types of problems.
Determining a method which given the features of a problem
creates a strategy schedule.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

23. Introduction Background Different approaches Latest successful projects Conclusion
ML for heuristics selection
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

24. Introduction Background Different approaches Latest successful projects Conclusion
ML for heuristics selection
Math point of view
Machine learning in this case is applied to predict the runtime of
an ATP over a specific class of problems in order to automatically
choose the best suitable strategy for a given unknown problem. For
each strategy s in the preselected strategies S, we are searching for
a function:
ρs : P → R (2)
such that for all problems p ∈ P the predicted values are close to
the actual runtimes: ρs(p) ∼ τ(p, s).
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

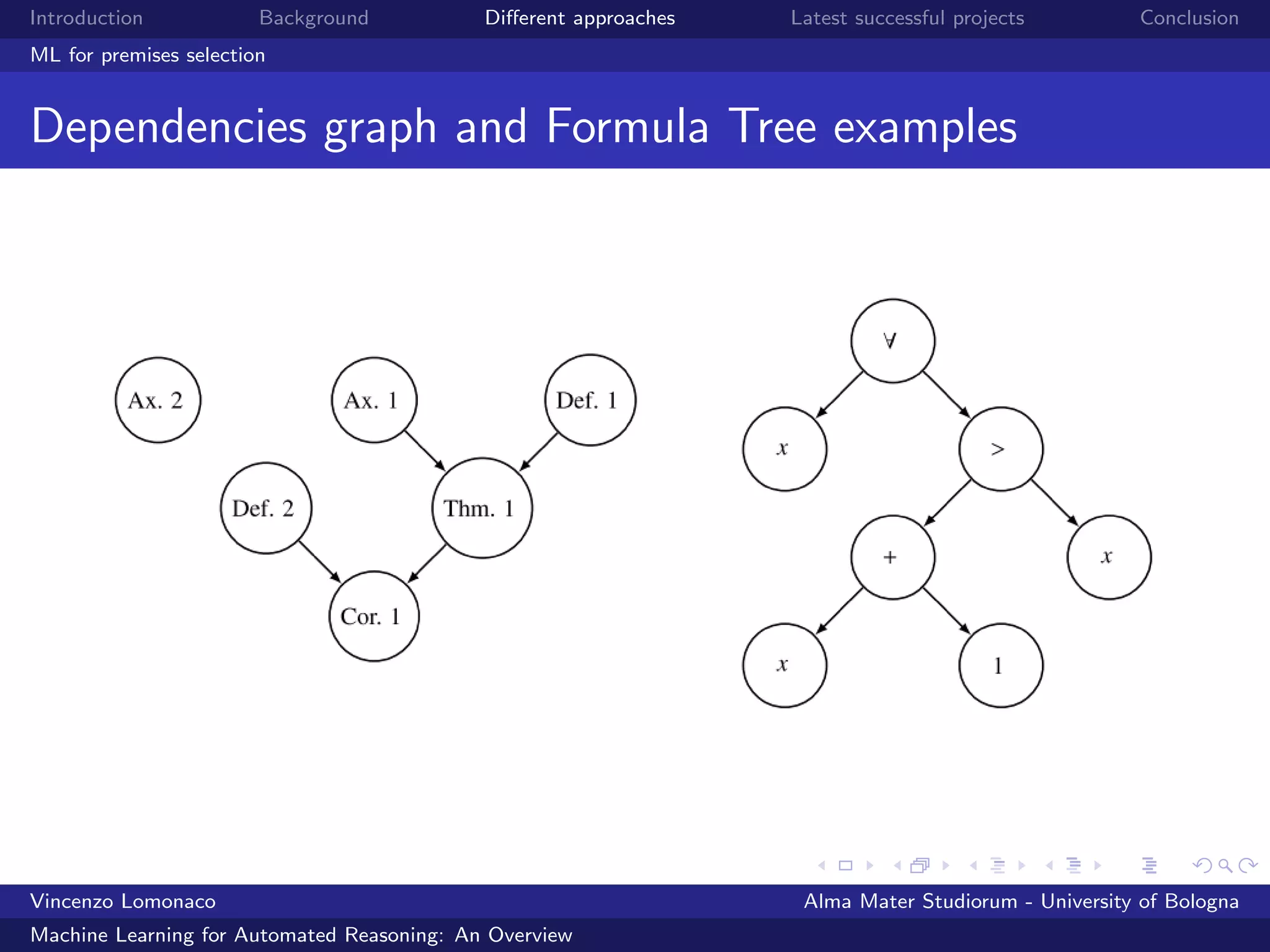
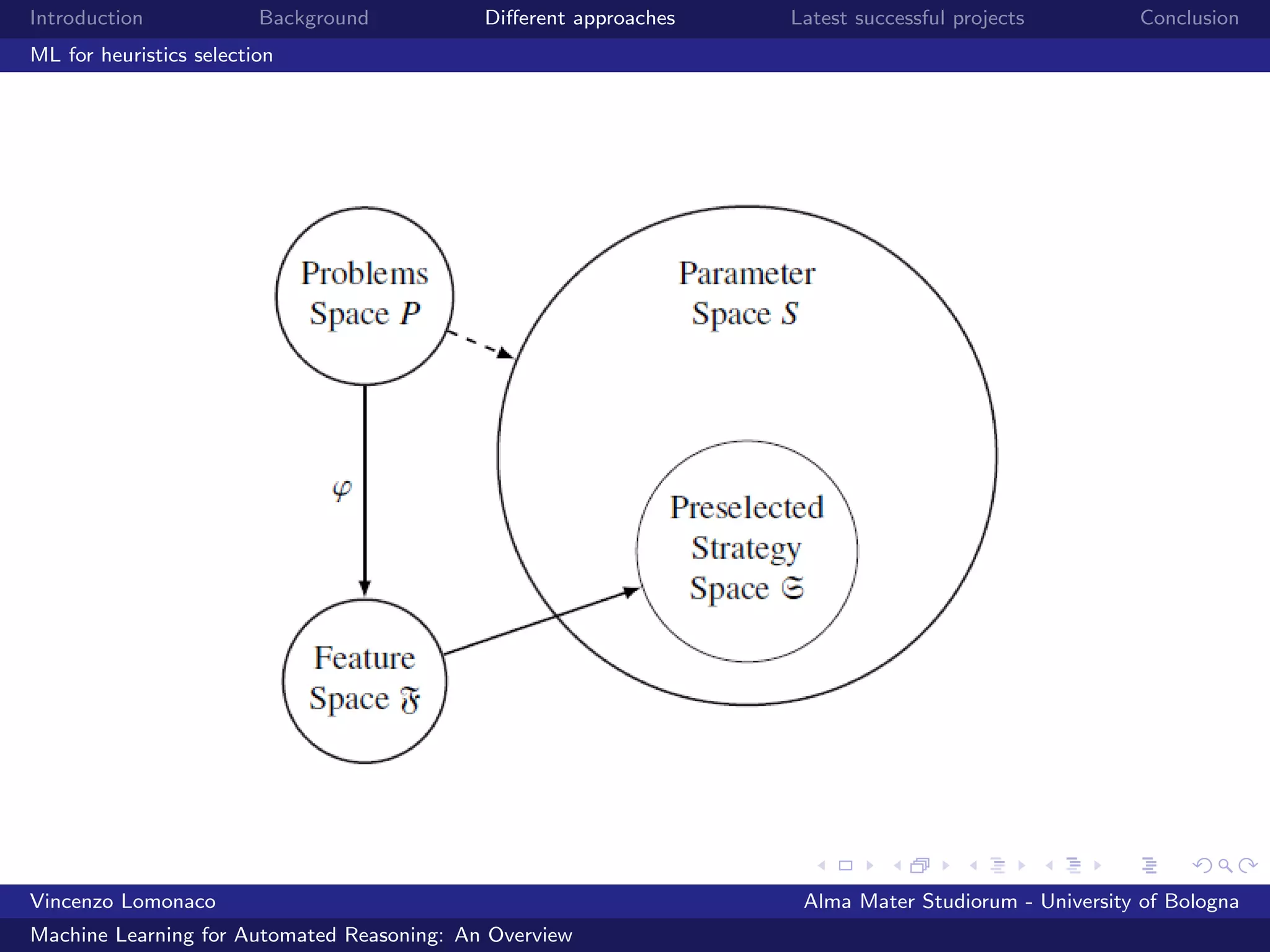
25. Introduction Background Different approaches Latest successful projects Conclusion
Latest successful projects I
ML4PG (machine learning extension for Proof General) [9] is
an interactive tool that provides statistical proof hints during
the process of Coq/SSReflect proof development.
MaSh (Machine Learning for Sledgehammer) [11], now part
of the default Isabelle installation, offers an alternative to
MePo (default relevance filter in Sledgehammer) by learning
from successful proofs.
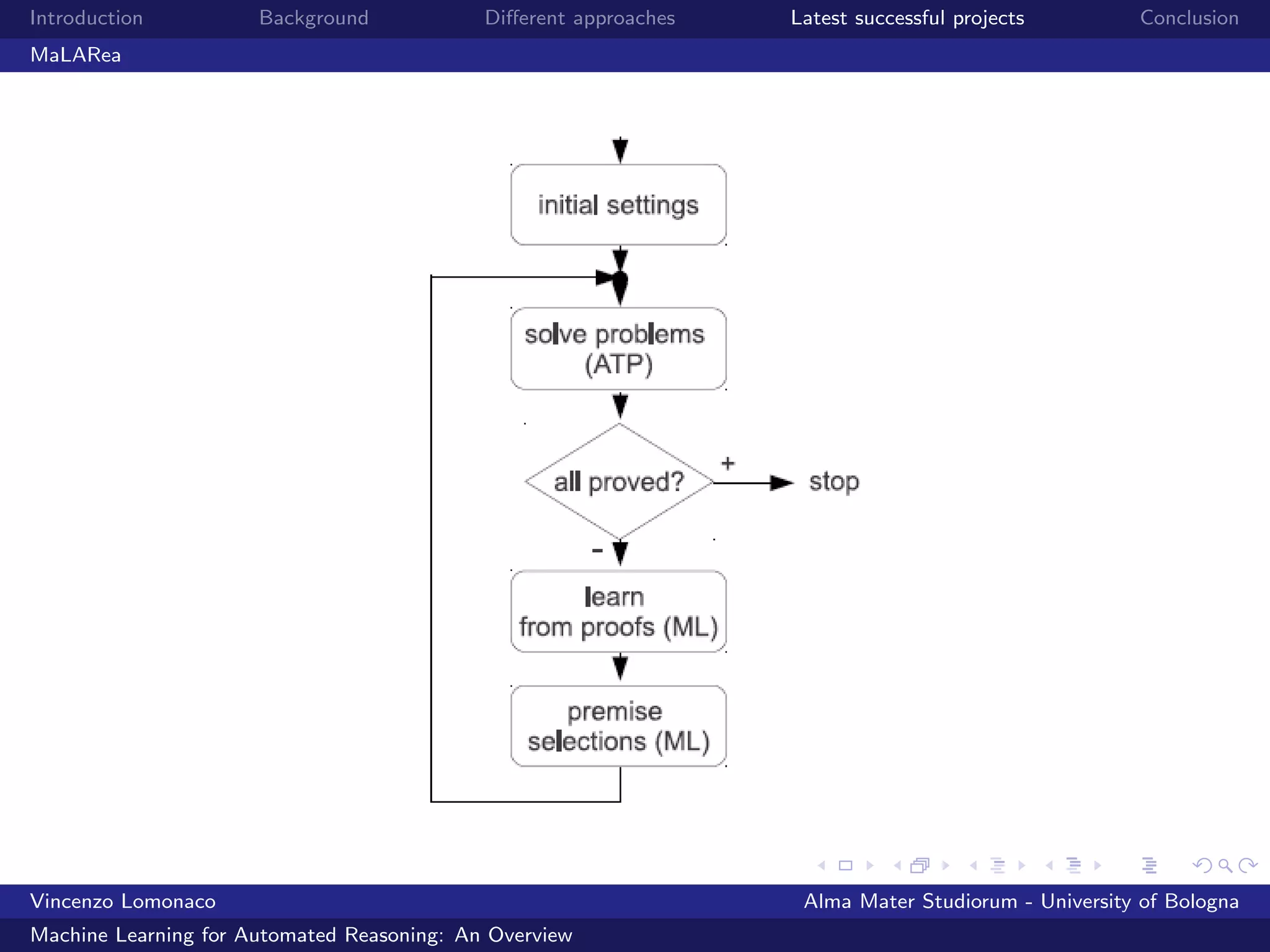
MaLARea (Machine Learner for Automated Reasoning) [23]
is a metasystem, which turns out to have so far the best
performance on large theory benchmarks like the MPTP
Challenge and MPTP2078.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

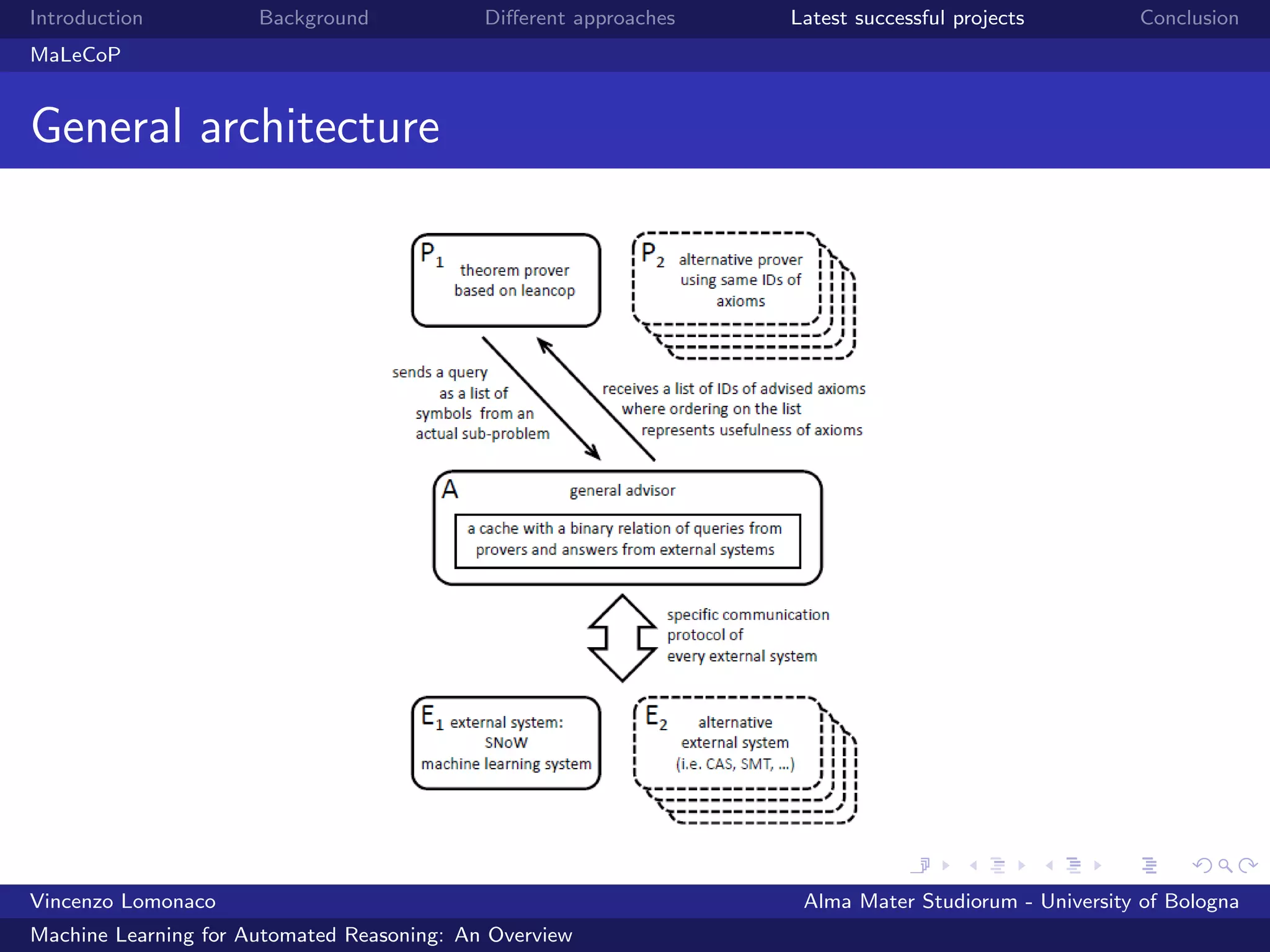
26. Introduction Background Different approaches Latest successful projects Conclusion
Latest successful projects II
MaLeCoP (Machine Learning Connection Prover) [24] is an
evolution of MaLARea where the learned knowledge is used
for guiding the proof search mechanisms inside a modified
version of leanCoP [14].
MaLeS (Machine Learning of Strategies) [11] is a framework
that develops strategies for ATPs and creates suitable
schedules of strategies for individual problems.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

27. Introduction Background Different approaches Latest successful projects Conclusion
ML4PG
ML4PG
ML4PG is an extension to Proof General (an Emacs based generic
interface for theorem provers) that uses state-of-the-art machine
learning techniques to interactively find proof patterns from Coq
and SS-Reflect proofs.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

28. Introduction Background Different approaches Latest successful projects Conclusion
ML4PG
How it works
It works on the background of Proof General, and extracts
some simple,low-level features from interactive proofs in
Coq/SSReflect;
On user’s request, it sends the gathered statistics to a chosen
machine-learning interface and triggers execution of a
clustering algorithm of the user’s choice;
It does some gentle post-processing of the results given by the
machine-learning tool, and displays families of related
proofs to the user.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

29. Introduction Background Different approaches Latest successful projects Conclusion
ML4PG
Extracted Features: An example I
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

30. Introduction Background Different approaches Latest successful projects Conclusion
ML4PG
Extracted Features: An example II
Every machine learning engine has its concrete format to represent
feature vectors; therefore, it is necessary to define translators to
adapt ML4PG’s internal encoding of feature vectors to the concrete
representation of the machine learning engine.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

31. Introduction Background Different approaches Latest successful projects Conclusion
ML4PG
ML engine
ML4PG engine is flexible to use all sorts of learning algorithms. Up
to now, it has been connected ML4PG to a variety of clustering
algorithms a family of unsupervised learning methods. Clustering
techniques divide data into n groups of similar objects (called clus-
ters), where the value of n is provided by the user.
The ML4PG user can interactively select different clustering algo-
rithms available in Matlab and Weka.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

32. Introduction Background Different approaches Latest successful projects Conclusion
MaSh
MaSh
MaSh, offers an alternative to MePo by learning from successful
proofs and not only ranking relevant promises based on syntactic
similarity.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

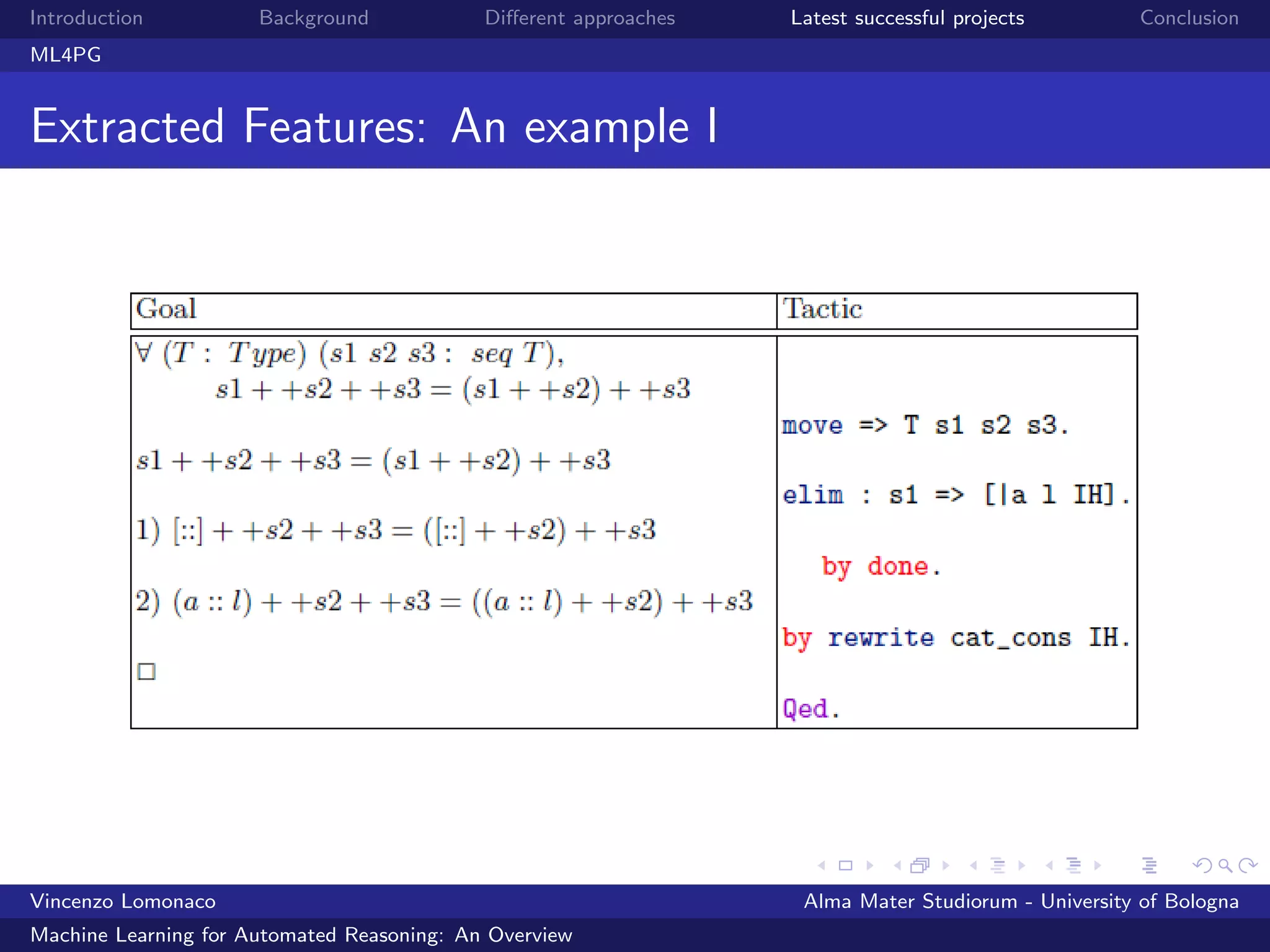
33. Introduction Background Different approaches Latest successful projects Conclusion
MaSh
MaSh’s heart
MaSh’s heart is a Python program that implements a custom ver-
sion of a weighted sparse naive Bayes algorithm that is faster
than the naive Bayes algorithm implemented in the SNoW [4]. This
Python program is used within a Standard ML module that inte-
grates machine learning with Isabelle. MaSh follows the ”four zeros”
philosophy meaning:
”Zero-configuration”
”Zero-click”
”Zero-maintenance”
”Zero-overhead”.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

34. Introduction Background Different approaches Latest successful projects Conclusion
MaSh
features used I
For each term in the formula, excluding the outer quantifiers, con-
nectives, and equality, the features are derived from the nontrivial
first-order patterns up to a given depth. Variables are replaced by
the wildcard (underscore). Given a maximum depth of 2, the term
g (h x a), where constants g, h, a originate from theories T, U, V ,
yields the patterns:
T.g( ) T.g(U.h( ; )) U.h( ; ) U.h( ; V .a) V .a
which are simplified and encoded respectively into the features:
T.g T.g(U.h) U.h U.h(V .a) V .a
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

35. Introduction Background Different approaches Latest successful projects Conclusion
MaSh
features used II
Types, excluding those of propositions, Booleans, and functions, are
encoded using an analogous scheme.
Type variables constrained by type classes give rise to features cor-
responding to the specified type classes and their superclasses.
Finally, various pieces of metainformation are encoded as features:
the theory to which the fact belongs; the kind of rule (e.g., introduc-
tion, simplification); whether the fact is local; whether the formula
contains any existential quantifiers or λ-abstractions.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

36. Introduction Background Different approaches Latest successful projects Conclusion
MaSh
Results
It was found that MaSh outperforms MePo on different datasets and
their combination (as a ensemble model) increases the number of
solved problems in the Judgement Day benchmark by 4.2% [11].
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

37. Introduction Background Different approaches Latest successful projects Conclusion
MaLARea
MaLARea
The closed loop between using deductive methods to find proofs,
and using inductive methods to learn from the existing proofs and
suggest new proof directions, is the main idea behind the MaLARea
metasystem.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

38. Introduction Background Different approaches Latest successful projects Conclusion
MaLARea
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

39. Introduction Background Different approaches Latest successful projects Conclusion
MaLARea
ML in MaLARea
There are many kinds of information that such an autonomous meta-
system can try to use and learn. The second version of MaLARea
already uses also structural and semantic features of formulas for
their characterization and for improving the axiom selection.
Successful runs provide additional data for learning (useful for solving
related problems), while unsuccessful runs can yield countermodels,
which can be re-used for semantic pre-selection and as additional
input features for learning.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

40. Introduction Background Different approaches Latest successful projects Conclusion
MaLARea
high-level approach
The communication between learning and the ATP systems is high-
level: The learned relevance is used to try to solve problems with
varied limited numbers of the most relevant axioms.
Pro:
MaLARea gives a generic inductive (learning)/deductive
(ATP) metasystem to which any ATP can be easily plugged
as a blackbox (E and SPASS by default).
Con:
it does not attempt to use the learned knowledge for guiding
the ATP search process once the axioms are selected.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

41. Introduction Background Different approaches Latest successful projects Conclusion
MaLeCoP
MaLeCoP
While in MaLARea learning-based axiom selection is done outside
unmodified theorem provers, in MaLeCoP the learning-based selec-
tion is done inside the prover, and the interaction between learning
of knowledge and its application is much finer.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

42. Introduction Background Different approaches Latest successful projects Conclusion
MaLeCoP
General architecture
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

43. Introduction Background Different approaches Latest successful projects Conclusion
MaLeCoP
ML in MaLeCoP I
The basic learning in MaLARea is used to associate conjecture sym-
bols with premises used in the conjecture’s proof. This learning
mode can be easily reproduced by MaLeCoP.
For learning clause selection on branches, instead, can be used
another information supplied by the prover: successful clause choices
done for particular paths in the proof.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

44. Introduction Background Different approaches Latest successful projects Conclusion
MaLeCoP
ML in MaLeCoP II
The information extracted from subtrees also contains the cost
(again in terms of inference numbers) of finishing the subtree.
In the original project the authors did not use this information yet in
learning, however They plan to use learning on this data for gradually
overcoming the most costly bad clause choices.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

45. Introduction Background Different approaches Latest successful projects Conclusion
MaLeS
MaLeS
MaLeS is a framework that develops strategies for automated
theorem provers (ATPs) and creates suitable schedules of strate-
gies for individual problems. The framework can be used in a push-
button way to develop such strategies and schedules for an arbitrary
ATP.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

46. Introduction Background Different approaches Latest successful projects Conclusion
MaLeS
MaLeS Solutions
With respect to the three main subproblems inherent the strategy
selection problem, MaLeS:
Perform a stochastic local search by taking previously
human-defined strategies as starting points of the search to
find a set of good preselected strategies.
Choose to use the well-known set of features designed by
Schulz for clause-normal-form and first order problems to
describe well each problem.
Uses kernels to learn the runtime prediction function and
schedule the strategies coherently.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

47. Introduction Background Different approaches Latest successful projects Conclusion
MaLeS
Features used
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

48. Introduction Background Different approaches Latest successful projects Conclusion
MaLeS
ML in MaLeS I
Kernels are a very popular machine learning method that has suc-
cessfully been applied in many domains [20]. A kernel can be seen
as a similarity function between feature vectors.
The kernel used in this project is the well-known Gaussian kernel
k with parameter σ of two problems p, q ∈ P with feature vectors
ϕ(p), ϕ(q) ∈ Ω ⊆ Rn for some n ∈ N is defined as:
K(p, q) := exp −
ϕ(p)T ϕ(p) − 2ϕ(p)T ϕ(q) + ϕ(q)T ϕ(q)
σ2
(3)
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

49. Introduction Background Different approaches Latest successful projects Conclusion
MaLeS
ML in MaLeS II
Let t ∈ R be a time limit. For each preselected strategy s ∈ S,
the ATP is run with strategy s and time limit t on each problem in
Ptrain. For each strategy Ps
train ⊆ Ptrain is the set of problems that
the ATP can solve within the time limit t with strategy s. In kernel
based machine learning, the prediction function s has the form:
ρs(p) =
q∈Ps
train
αs
qK(p, q) (4)
Then, having defined the prediction functions, for each new prob-
lem, MaLeS uses the prediction functions to select the strategy and
runtime that is most likely to solve the problem. If the predicted
strategy does not solve the problem, MaLeS updates all prediction
functions with this new information.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

50. Introduction Background Different approaches Latest successful projects Conclusion
Conclusion I
In this talk, we have been discussing a rapidly emerging research
trend that aims to bring machine learning to theorem proving and,
more in general, to automated reasoning.
Early results are promising, considering the fact that very few people
are working in this direction.
Then, we have presented different approaches taken in this context
and a few successful project as use cases.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

51. Introduction Background Different approaches Latest successful projects Conclusion
Conclusion II
Talking about future directions, the next step could be, of course,
to try more advanced ML algorithms along with unsupervised fea-
ture extraction methods bringing more expertise from the AI/ML
community.
On the long run, the heuristic and machine learning methods, and
combined AI metasystems, have a very long way to go. This is
no longer only about mathematics: all kinds of more or less formal
large knowledge bases are becoming available in other sciences, and
automated reasoning could become one of the strongest methods
for general reasoning in sciences when sufficient amount of formal
knowledge exists.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

52. Introduction Background Different approaches Latest successful projects Conclusion
References I
Ethem Alpaydin.
Introduction to machine learning.
MIT press, 2004.
Andrea Asperti, Wilmer Ricciotti, Claudio Sacerdoti Coen, and Enrico
Tassi.
The matita interactive theorem prover.
In Automated Deduction–CADE-23, pages 64–69. Springer, 2011.
Yves Bertot and Pierre Cast´eran.
Interactive theorem proving and program development: Coq’Art: the
calculus of inductive constructions.
springer, 2004.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

53. Introduction Background Different approaches Latest successful projects Conclusion
References II
Andrew Carlson, Chad Cumby, Jeff Rosen, and Dan Roth.
The snow learning architecture.
Technical report, Technical report UIUCDCS, 1999.
Leonardo De Moura and Nikolaj Bjørner.
Z3: An efficient smt solver.
In Tools and Algorithms for the Construction and Analysis of Systems,
pages 337–340. Springer, 2008.
Kurt G¨odel.
¨Uber formal unentscheidbare s¨atze der principia mathematica und
verwandter systeme i.
Monatshefte f¨ur mathematik und physik, 38(1):173–198, 1931.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

54. Introduction Background Different approaches Latest successful projects Conclusion
References III
Adam Grabowski, Artur Kornilowicz, and Adam Naumowicz.
Mizar in a nutshell.
Journal of Formalized Reasoning, 3(2):153–245, 2010.
John Harrison.
Hol light: A tutorial introduction.
In Formal Methods in Computer-Aided Design, pages 265–269. Springer,
1996.
J´onathan Heras and Ekaterina Komendantskaya.
Ml4pg: proof-mining in coq.
CoRR, 2013.
Matt Kaufmann, J Strother Moore, and Panagiotis Manolios.
Computer-aided reasoning: an approach.
Kluwer Academic Publishers, 2000.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

55. Introduction Background Different approaches Latest successful projects Conclusion
References IV
Daniel A K¨uhlwein.
Machine learning for automated reasoning.
2013.
Huan Liu and Hiroshi Motoda.
Feature selection for knowledge discovery and data mining.
Springer, 1998.
Tobias Nipkow, Lawrence C Paulson, and Markus Wenzel.
Isabelle/HOL: a proof assistant for higher-order logic, volume 2283.
Springer, 2002.
Jens Otten and Wolfgang Bibel.
leancop: lean connection-based theorem proving.
Journal of Symbolic Computation, 36(1):139–161, 2003.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

56. Introduction Background Different approaches Latest successful projects Conclusion
References V
Sam Owre and Natarajan Shankar.
A brief overview of pvs.
In Theorem Proving in Higher Order Logics, pages 22–27. Springer, 2008.
Arthur William Quaife et al.
Automated development of fundamental mathematical theories.
1990.
Alexandre Riazanov and Andrei Voronkov.
The design and implementation of vampire.
AI communications, 15(2):91–110, 2002.
Bertrand Russell and Alfred North Whitehead.
Principia mathematica vol.
1925.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

57. Introduction Background Different approaches Latest successful projects Conclusion
References VI
Stephan Schulz.
E-a brainiac theorem prover.
Ai Communications, 15(2):111–126, 2002.
John Shawe-Taylor and Nello Cristianini.
Kernel methods for pattern analysis.
Cambridge university press, 2004.
Konrad Slind and Michael Norrish.
A brief overview of hol4.
In Theorem Proving in Higher Order Logics, pages 28–32. Springer, 2008.
Josef Urban.
Translating mizar for first order theorem provers.
In Mathematical Knowledge Management, pages 203–215. Springer, 2003.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview

58. Introduction Background Different approaches Latest successful projects Conclusion
References VII
Josef Urban.
Malarea: a metasystem for automated reasoning in large theories.
ESARLT, 257, 2007.
Josef Urban, Jiˇr´ı Vyskoˇcil, and Petr ˇStˇep´anek.
Malecop machine learning connection prover.
In Automated Reasoning with Analytic Tableaux and Related Methods,
pages 263–277. Springer, 2011.
Christoph Weidenbach, Dilyana Dimova, Arnaud Fietzke, Rohit Kumar,
Martin Suda, and Patrick Wischnewski.
Spass version 3.5.
In Automated Deduction–CADE-22, pages 140–145. Springer, 2009.
Vincenzo Lomonaco Alma Mater Studiorum - University of Bologna
Machine Learning for Automated Reasoning: An Overview