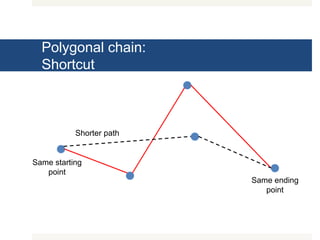
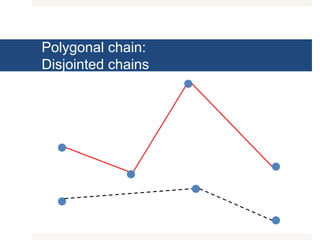
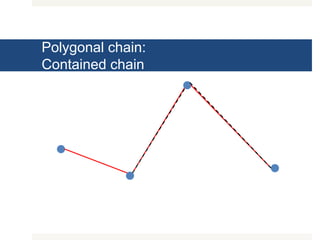
The document outlines various exercises and functions related to linked lists and polygonal chains, covering operations such as summing elements, finding maximum and minimum values, reversing a list, and identifying peaks. It also describes functions for manipulating polygonal chains, including checking for shortcuts, disjointedness, and containment relations. Additionally, it introduces further exercises regarding extensions, concatenation, and tortuosity of polygonal chains.

1. Linked lists
Exercises
Eleonora Ciceri, Politecnico di Milano
Email: eleonora.ciceri@polimi.it

2. Simple exercises

3. Sum of list elements
 Let sumElements() be the function that:
 Gets as input parameters:
 The list head
 An integer M
 Returns the sum of the values in the list that are multiples of M

4. Sum of list elements
ListNode* currentNode = head;
int sum = 0;
while (currentNode != NULL) {
if (currentNode->data % M == 0)
sum = sum + currentNode->data;
currentNode = currentNode->nextPtr;
}
return sum;

5. Maximum value in a list (recursive)
 Write a recursive function that retrieves the maximum element
in a list
 Base case?
 Recursion step?

6. Maximum value in a list (recursive)
int findMax(ListNode* head) {
if (head == NULL)
return -1; // Assuming values will be all positive
else
return std::max(head->data,
findMax(head->nextPtr));
}

7. Even minimum number
 Define a function that, given a list of integer numbers, returns
the position (pointer) of the even minimum element in the list

8. Even minimum number
int findEvenMin(ListNode* head) {
ListNode* currentNode = head;
int min = std::numeric_limits<int>::max();
while (currentNode != NULL) {
if (currentNode->data % 2 == 0)
min = std::min(currentNode->data, min);
currentNode = currentNode->nextPtr;
}
return min;
}

9. Reverse print of the list
 Write a function that prints the values in the list in reverse
order with respect to the order in which they are stored in the
list

10. Reverse print of the list
void inversePrint(ListNode* head) {
if (head == NULL)
return;
else {
inversePrint(head->nextPtr);
std::cout << "- " << head->data << std::endl;
}
}

11. Find peaks
 Write a function that takes a list and finds its peaks
 The peaks are defined as values preceded and followed by
values that are smaller than their own half

12. Find peaks
std::vector<int> findPeaks(ListNode* head) {
ListNode* currentNode = head->nextPtr;
ListNode* previousNode = head;
std::vector<int> peaks;
while (currentNode != NULL) {
if (previousNode->data < (float)currentNode->data/2 &&
currentNode->nextPtr->data < (float)currentNode->data/2)
peaks.push_back(currentNode->data);
previousNode = currentNode;
currentNode = currentNode->nextPtr;
}
return peaks;
}

13. Complex exercises

14. Polygonal chain
 A polygonal chain is a connected series of line segments; we
suppose such segments are composed of points which are all
different between each other
 The length of such polygonal chain is the summation of the
distances between two consecutive points
 Naming convention
 Two polygonal chains are disjointed if they do not share any point
 B is a shortcut for A if B shares the same starting and ending point of
A, but is shorter
 A contains B if B is a subsequence of the points in A

15. Polygonal chain
 Write the following functions:
 Shortcut: tells if B is a shortcut of A
 Disjoint: tells if A and B are disjointed
 Contains: tells if A contains B

16. Polygonal chain:
Shortcut
Same starting
point
Same ending
point
Shorter path

17. Polygonal chain:
Shortcut(extreme points)
LineNode* findFirstElement(LineNode* list) {
return list;
}
LineNode* findLastElement(LineNode* list) {
while (list->nextPtr != NULL)
list = list->nextPtr;
return list;
}

18. Polygonal chain:
Shortcut(length)
float computeLineLength(LineNode* head) {
LineNode* currentNode = head->nextPtr;
LineNode* previousNode = head;
float length = 0;
while (currentNode != NULL) {
length += computeDistance(currentNode, previousNode);
previousNode = currentNode;
currentNode = currentNode->nextPtr;
}
return length;
}

19. Polygonal chain:
Shortcut(distance between two points)
float computeDistance(LineNode* firstPt, LineNode* secondPt) {
int x1 = firstPt->x;
int y1 = firstPt->y;
int x2 = secondPt->x;
int y2 = secondPt->y;
int distance = std::sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
return distance;
}

20. Polygonalchain:
Shortcut
bool isShortcut(LineNode* A, LineNode* B) {
if (A == NULL || B == NULL)
return false;
LineNode* firstElementA = findFirstElement(A);
LineNode* lastElementA = findLastElement(A);
LineNode* firstElementB = findFirstElement(B);
LineNode* lastElementB = findLastElement(B);
if (firstElementA->x == firstElementB->x &&
firstElementA->y == firstElementB->y &&
lastElementA->x == lastElementB->x &&
lastElementB->y == lastElementB->y) {
float lengthA = computeLineLength(A);
float lengthB = computeLineLength(B);
if (lengthB < lengthA)
return true;
else
return false;
}
else
return false;
}

21. Polygonal chain:
Disjointed chains

22. Polygonalchain:
Disjointedchains
bool isDisjointed(LineNode* A, LineNode* B) {
bool disjointed = true;
LineNode* currentNodeA = A;
while (currentNodeA != NULL) {
LineNode* currentNodeB = B;
int xA = currentNodeA -> x;
int yA = currentNodeA -> y;
while (currentNodeB != NULL) {
int xB = currentNodeB -> x;
int yB = currentNodeB -> y;
if (xA == xB && yA == yB) {
disjointed = false;
break;
}
currentNodeB = currentNodeB -> nextPtr;
}
if (disjointed == false)
break;
currentNodeA = currentNodeA -> nextPtr;
}
return disjointed;
}

23. Polygonal chain:
Contained chain

24. Polygonalchain:
Containedchain
bool isEqualFromHere(LineNode* A, LineNode*B) {
LineNode* currentNodeA = A;
LineNode* currentNodeB = B;
bool equal = true;
while (currentNodeA != NULL && currentNodeB != NULL) {
int xA = currentNodeA->x;
int yA = currentNodeA->y;
int xB = currentNodeB->x;
int yB = currentNodeB->y;
if (xA != xB || yA != yB) {
equal = false;
break;
}
currentNodeA = currentNodeA->nextPtr;
currentNodeB = currentNodeB->nextPtr;
}
if (currentNodeA == NULL && currentNodeB != NULL)
equal = false;
return equal;
}

25. Polygonalchain:
Containedchain
bool isContained(LineNode* A, LineNode* B) {
LineNode* currentNodeA = A;
bool contained = false;
LineNode* currentNodeB = B;
int xB = currentNodeB->x;
int yB = currentNodeB->y;
while (currentNodeA != NULL) {
int xA = currentNodeA->x;
int yA = currentNodeA->y;
if (xA == xB && yA == yB)
contained = isEqualFromHere(currentNodeA,
currentNodeB);
if (contained == true)
break;
currentNodeA = currentNodeA -> nextPtr;
}
return contained;
}

26. Polygonal chain
 Additional exercises:
 Define the extension function, which tells if A extends B; A
extends B if A contains B and (A,B) share the ending point
 Define the concatenate function, which returns the concatenation
of B after A
 Define the tortuosity function, which returns the ratio between the
length of A and the distance between its extreme points