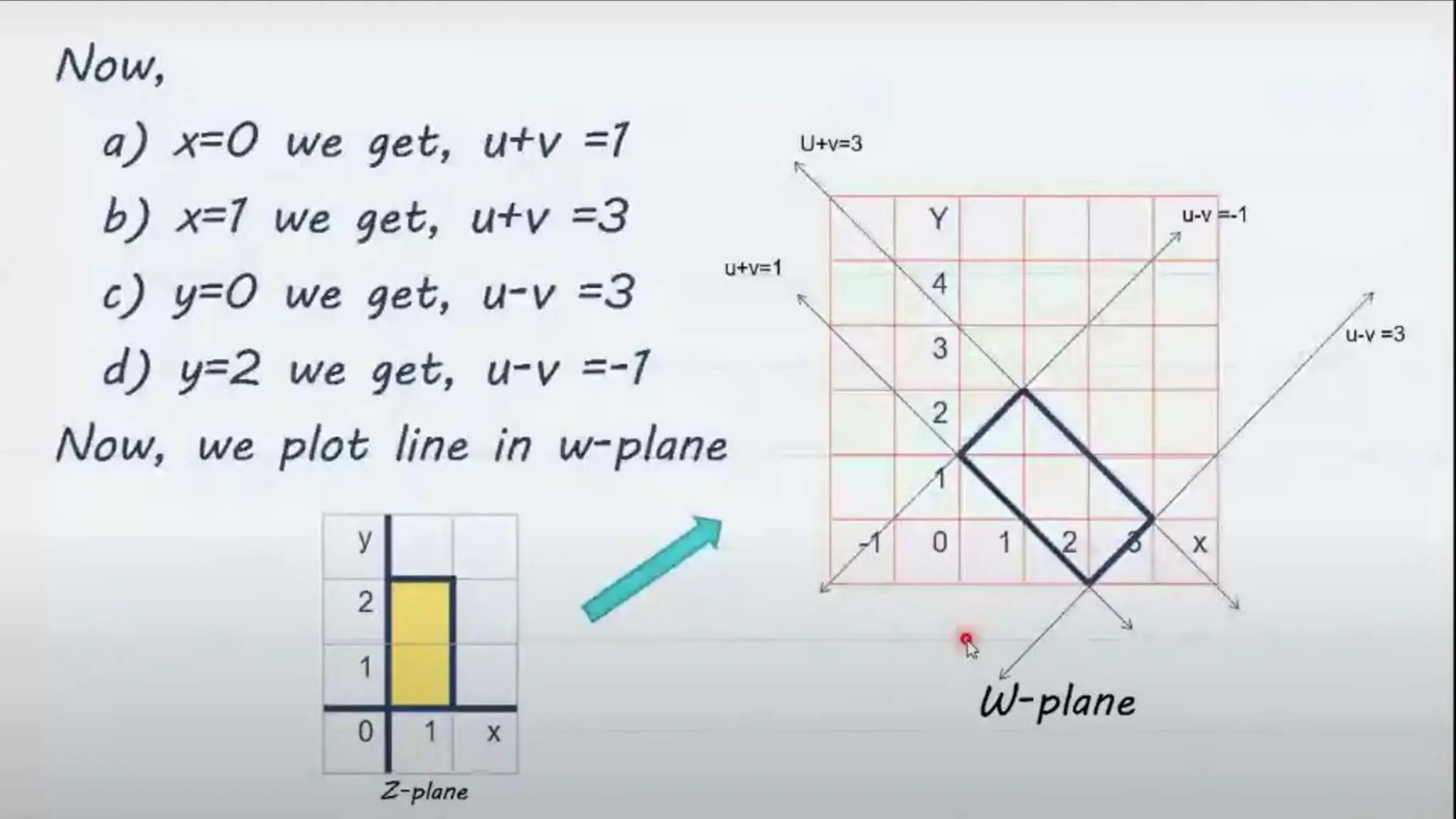
This document discusses linear and bilinear mappings. It begins by defining mapping as the process of associating elements between sets. Linear mapping is described as a mathematical function that transforms data using a matrix, having properties like linearity and additivity. It provides examples of linear mapping applications in areas like engineering, data analysis, and physics. Bilinear mapping is then introduced as a mapping that combines elements from two vector spaces to return a scalar value. The document notes differences between linear and bilinear mappings and provides concluding remarks about their respective applications and importance.

1. LINEAR AND BILINEAR
MAPPING
TEAM MEMBERS
SANIKA RANE – 45 PRAVYA SHETTY - 34
NIHAL SHETTY – 26 SANKET KATAKE - 47

2. WHAT IS MAPPING ?
 Mapping is the process of associating or transforming elements
from one set to elements in another set.
 Mapping refers to the relationship or correspondence between
elements of one set and elements of another set, often defined by
a specific rule or function.
 It is a fundamental concept used to describe how information,
data, or variables are transformed from one representation or
domain to another.

3. LINEAR MAPPING
 Linear Mapping is a Mathematical Function that transforms one set of data
into another by multiplying it with a matrix.
 Linear Mapping has several properties which include
 Linearity
 Homogeneity
 Additivity
 These properties make it a powerful tool for transforming data in a consistent
and predictable way.
 It is used in a wide range of applications, from computer graphics to machine
learning

4. APPLICATIONS OF LINEAR MAPPING
 Linear Mapping helps to determine voltage and current distributions in
linear components like resistors, capacitors, and inductors.
 Engineers use it to model and predict relationships between variables,
making them valuable in data analysis.
 Linear mappings are used to analyze and solve linear differential
equations that describe physical systems, including mechanical
vibrations, heat transfer, and fluid flow.

5. 1/2
STEPS TO SOLVE
Identify the given
vectors, matrices,
and the specific
linear
transformation
you need to
Perform.
Represent the
linear
transformation as a
matrix. If you have
a vector x and a
matrix A, the
transformation can
be written as Ax.
Multiply the given
vector(s) by the
transformation matrix
using
matrix
multiplication rules. If
you have multiple
vectors, perform the
multiplication for each
One.
1 2 3

6. 2/2
The result of the
matrix multiplication
will give you the
transformed vector(s).
These vectors
represent the new
coordinates in the
transformed space.
Represent the
linear
transformation as a
matrix. If you have
a vector x and a
matrix A, the
transformation can
be written as Ax.
Represent the
linear
transformation as
matrix. If you have
a vector x and a
matrix A, the
transformation can
be written as Ax.
Depending on the
problem, you might
need to check
properties like
linearity,
invertibility, or
orthogonality of the
Transformation.
n some cases, you
might needto
perform additional
operations on the
transformed vectors,
such as finding
norms, angles, or
solving linear
equations. Provide
the final transformed
vectors or the
specific solution to
the problem,
depending on what
was asked.
4 5 6
7
STEPS TO SOLVE

9. BILINEAR MAPPING
 Bilinear mapping is a type of mapping that combines elements
from two different vector spaces and returns a scalar value.
 It is a more specialized concept than linear mappings and is often
used to describe certain mathematical operations and
transformations encountered in engineering and physics.

10. APPLICATION OF BILLINEAR MAPPING
 In fluid dynamics simulated properties like describe interactions between
bilinear mappings describe interactions between fluid properties like velocity
and pressure.
 Bilinear mappings are applied in seismic and electromagnetic surveys to
model the interactions of waves with underground structures, helping
geophysicists locate and analyze subsurface resources or geological features.
 Bilinear mappings are used for texture mapping and interpolation in
computer graphics, allowing for realistic rendering of surfaces in 3D graphics
and video games.

15. DIFFRENCES
 Linear Mapping transforms one
set of data.
 Linear Mapping is simple to
solve than Bilinear mapping.
 Bilinear Mapping transforms
two sets of data.
 Bilinear Mapping is more
complex.
LINEAR MAPPING BILINEAR MAPPING

16. CONCLUSION
 Linear mappings, characterized by preserving vector addition and scalar
multiplication, are foundational tools for solving linear systems of equations,
which are ubiquitous in engineering disciplines like electrical circuits,
structural analysis, and control systems.
 These mappings simplify complex problems by leveraging the principles of
linearity.

17. CONCLUSION
 Bilinear mappings, on the other hand, are crucial in areas where
interactions between two variables are nonlinear.
 Engineering applications such as stress analysis in materials, fluid
dynamics, and optimization often involve bilinear relationships.
 These mappings allow engineers to model and analyze systems
with more intricate behavior, providing a deeper understanding of
the physical world.

18. THANK YOU