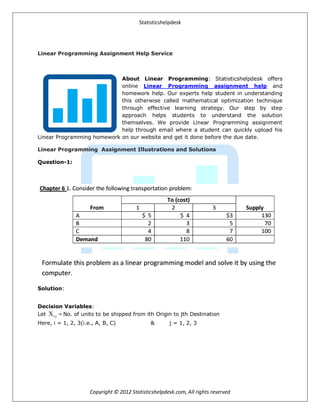
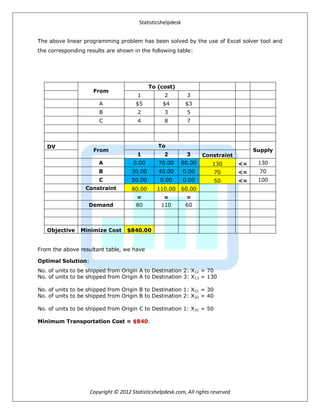
Statisticshelpdesk offers online linear programming assignment help and homework help. Their experts help students understand linear programming, a mathematical optimization technique, through effective learning strategies. They provide step-by-step solutions to help students solve problems themselves. Students can quickly upload linear programming homework to the website and get it completed before the due date. The document then provides an example linear programming problem involving minimizing transportation costs with decision variables, constraints, and the optimal solution found using Excel solver. Contact information is given at the end.

1. Statistics Help Desk
Linear Programming Assignment Help Service
Alex Gerg

2. Statisticshelpdesk
Copyright © 2012 Statisticshelpdesk.com, All rights reserved
Linear Programming Assignment Help Service
About Linear Programming: Statisticshelpdesk offers
online Linear Programming assignment help and
homework help. Our experts help student in understanding
this otherwise called mathematical optimization technique
through effective learning strategy. Our step by step
approach helps students to understand the solution
themselves. We provide Linear Programming assignment
help through email where a student can quickly upload his
Linear Programming homework on our website and get it done before the due date.
Linear Programming Assignment Illustrations and Solutions
Question-1:
Solution:
Decision Variables:
Let jiX No. of units to be shipped from ith Origin to jth Destination
Here, i = 1, 2, 3(i.e., A, B, C) & j = 1, 2, 3

3. Statisticshelpdesk
Copyright © 2012 Statisticshelpdesk.com, All rights reserved
Formulation of Linear Programming Model:
Minimize Z = $5X11 + 4X12 + 3X13 + 2X21 + 3X22 + 5X23 + 4X31 + 8X32 + 7X33
Subject to the constraint
X11 + X12 + X13 ≤ 130
X21 + X22 + X23 ≤ 70
X31 + X32 + X33 ≤ 100
X11 + X21 + X31 = 80
X12 + X22 + X32 = 110
X13 + X23 + X33 = 60
All Xi,j ≥ 0

4. Statisticshelpdesk
Copyright © 2012 Statisticshelpdesk.com, All rights reserved
The above linear programming problem has been solved by the use of Excel solver tool and
the corresponding results are shown in the following table:
From
To (cost)
1 2 3
A $5 $4 $3
B 2 3 5
C 4 8 7
DV
From
To
Supply
1 2 3 Constraint
A 0.00 70.00 60.00 130 <= 130
B 30.00 40.00 0.00 70 <= 70
C 50.00 0.00 0.00 50 <= 100
Constraint 80.00 110.00 60.00
= = =
Demand 80 110 60
Objective Minimize Cost $840.00
From the above resultant table, we have
Optimal Solution:
No. of units to be shipped from Origin A to Destination 2: X12 = 70
No. of units to be shipped from Origin A to Destination 3: X13 = 130
No. of units to be shipped from Origin B to Destination 1: X21 = 30
No. of units to be shipped from Origin B to Destination 2: X22 = 40
No. of units to be shipped from Origin C to Destination 1: X31 = 50
Minimum Transportation Cost = $840.

5. Statisticshelpdesk
Copyright © 2012 Statisticshelpdesk.com, All rights reserved
Contact Us:
Phone: +44-793-744-3379
Mail Us: info@statisticshelpdesk.com
Web: www.statisticshelpdesk.com
Facebook: https://www.facebook.com/Statshelpdesk
Twitter: https://twitter.com/statshelpdesk
Blog: http://statistics-help-homework.blogspot.com/

6. Statisticshelpdesk
Copyright © 2012 Statisticshelpdesk.com, All rights reserved