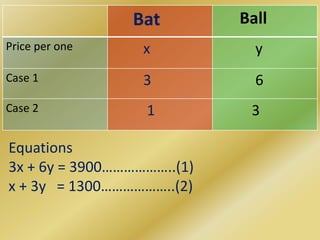
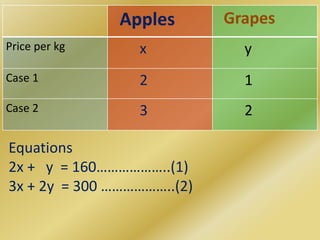
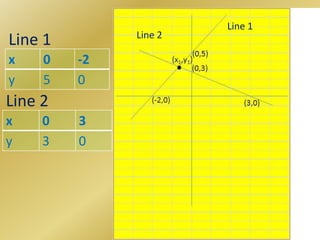
This document contains examples of solving systems of linear equations through elimination and cross-multiplication methods. It includes two examples of representing word problems algebraically with two equations each and solving for the unknown variables. It also briefly discusses the general form of a linear equation representing a line and provides an example of using cross-multiplication to solve a system of two equations.

1. Pair of Linear EquationsClass XCBSE

2. Example 1Seven years ago A was seven times as old as B was then. Three years from now, A will be three times as old as B then. Represent this algebraically and find their present ages.

3. Equations Simplifiedx - 7y + 42 = 0 …..(1)x - 3y - 6 = 0 …..(2)Equationsx – 7 = 7(y - 7)x + 3 = 3(y + 3)

4. Solution by Eliminationx - 7y = - 42 …..(1) x - 3y = 6 …..(2) ----------------------------(1) – (2): -4y = -48 y = 48/4 = 12Substitute in (2): x – 36 = 6 x = 36 + 6 = 42A’s present age = 42B’s present age = 12

5. Example 2x - 7y + 42 = 0 …..(1)x - 3y - 6 = 0 …..(2)……………………………….a1 = 1, b1 = -7, c1 = 42a2 = 1, b2 = -3, c2 = -6…………………………………

7. Example 3Sania buys 3 bats and 6 balls for Rs 3900. Later she buys another batand 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and find the price of a bat and that of a ball.

8. Equations3x + 6y = 3900………………..(1)x + 3y = 1300………………..(2)

9. Solution by elimination: 3x + 6y = 3900………………(1) x + 3y = 1300 ………………(2) -----------------(1)…………………….. 3x + 6y = 3900…………..(3)(2)x3…………………. 3x + 9y = 3900……………(4) --------------------(4)-(3)………………… 3y = 0 y = 0 x = 1300What’s your conclusion?Try this using the Cross-Multiplication method.

10. Example 3The cost of 2 kg of apples and 1 kg of grapes is Rs 160 and that of 3 kg of apples and 2 kg of grapes is Rs 300. Represent this situation algebraically and find the price per kg of apples and grapes.

11. Equations2x + y = 160………………..(1)3x + 2y = 300 ………………..(2)

12. Solution by elimination: 2x + y = 160………………..(1) 3x + 2y = 300………………..(2) ---------------------------- (1)x2…………….. 4x + 2y = 320…………..(3)(2)…………………. 3x + 2y = 300……………(4) --------------------(3)-(4)………………… x = 20 (1)……………………. y = 120What’s your conclusion?Try this using the Cross-Multiplication method.

13. Graphical SolutionGeneral Linear Equation:ax + by + c = 0This represents a line.

15. Example 4: Cross-Multiplication5x – 2y + 10 = 0……………………..(1)3x + 3y - 9 = 0………………………(2)-------------------a1 = 5, b1 = -2, c1 = 10a2 = 3, b2 = 3, c2 = -9

16. Line 1Line 1Line 2Line 2

17. The EndFor any clarification please contactvattamattam@gmail.com