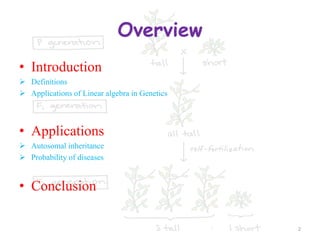
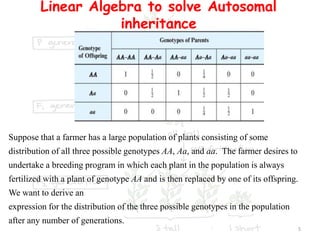
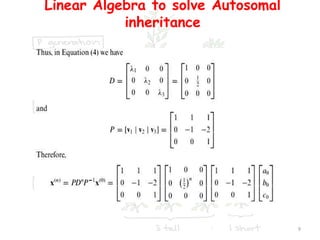
Linear algebra concepts such as matrices and linear transformations can be used to model autosomal inheritance in plant populations. The genotype distributions over successive generations can be represented by a matrix M. Diagonalizing M yields an explicit expression for the genotype distribution matrix Mn at any generation n. Specifically, applying the breeding program of always mating plants with genotype AA shows that eventually only genotype AA plants will remain, with the other genotypes disappearing over time. Thus linear algebra provides a way to analyze and predict the effects of inheritance and breeding programs on trait distributions in plant populations.

1. Linear Algebra to solve Autosomal
inheritance
Course Title: Linear Algebra and Complex Variables
Course Code: MAT205
Section: 06
Course Instructor: Ahsan Ali
Senior Lecturer (Mathematics)
Presented by: Group [B]
Abdullah al bayezid
Rakib Ahmed
Richita Islam
Md. Shabab Mehebub
1

2. Overview
• Introduction
 Definitions
 Applications of Linear algebra in Genetics
• Applications
 Autosomal inheritance
 Probability of diseases
• Conclusion
2

3. Introduction
• Genetics: The study of the inheritance of traits.
• Gene: A section of DNA that influences the heredity of a trait.
• Linear algebra: It is the branch of mathematics concerning
vector spaces and linear mappings between such spaces.
Transformation of matrix is one of the part of them.
• Autosomal inheritance: Is one pattern of inheritance for a
trait, disease, or disorder to be passed on through families
• Transformation of matrix: In Linear algebra, linear
transformation can be represented by matrices. 3

4. Applications of Linear algebra in
Genetics
• In humans, color blindness, hereditary baldness, hemophilia are
traits controlled by X-linked inheritance and cystic fibrosis,
sickle-cell anemia and Cooley’s anemia occurred because of
autosomal recessive inheritance.
• Investigation can be occurred for the propagation of an
inherited trait in successive generations by computing powers
of a matrix.
• By calculating eigenvalues, eigenvectors and matrix rotation
autosomal recessive inheritance diseases effectiveness could be
counted.
4

5. Linear Algebra to solve Autosomal
inheritance
Suppose that a farmer has a large population of plants consisting of some
distribution of all three possible genotypes AA, Aa, and aa. The farmer desires to
undertake a breeding program in which each plant in the population is always
fertilized with a plant of genotype AA and is then replaced by one of its offspring.
We want to derive an
expression for the distribution of the three possible genotypes in the population
after any number of generations.
5

6. For n = 0, 1, 2, . . . , let us set
an = fraction of plants of genotype AA in nth generation
bn = fraction of plants of genotype Aa in nth generation
cn = fraction of plants of genotype aa in nth generation
Thus a0, b0, and c0 specify the initial distribution of the genotypes. We also
have that
an + bn + cn = 1 for n = 0, 1, 2, . . .
From that Table we can determine the genotype distribution of each
generation from the genotype distribution of the preceding generation by
the following equations:
an = an-1 + ½ bn-1
bn = cn-1 + ½ bn-1 n = 1, 2, . . . (1)
cn = 0
Linear Algebra to solve Autosomal
inheritance
6

7. Linear Algebra to solve Autosomal
inheritance
For example, the first of these three equations states that all the offspring of a
plant of genotype AA will be of genotype AA under this breeding program and
that half of the offspring of a plant of genotype Aa will be of genotype AA.
Equations (1) can be written in matrix notation as
x(n) = Mx(n-1) , n = 1, 2, . . . (2)
where
(3)
7

8. Linear Algebra to solve Autosomal
inheritance
Consequently, if we can find an explicit expression for Mn, we can use (3) to obtain
an explicit expression for x(n) . To find an explicit expression for Mn , we first
diagonalize M. That is, we find an invertible matrix P and a diagonal matrix D
such that
M = PDP -1 (4)
8

9. Linear Algebra to solve Autosomal
inheritance
9

10. Linear Algebra to solve Autosomal
inheritance
(5)
10

11. Linear Algebra to solve Autosomal
inheritance
Result: Therefore, an= plants of genotype AA=1 .
So, It will be expressed.
But, as bn =0 and cn=0
So, there genotype respectively Aa and aa will not be expressed.
11

12. Probability of diseases
Autosomal inheritance Diseases:
 By following the calculation of inheritance in which a normal
gene A dominates an abnormal gene a. Genotype AA is a normal
individual; genotype Aa is a carrier of the disease but is not
afflicted with the disease; and genotype aa is afflicted with the
disease. All the offspring of a plant of genotype AA will be of
genotype AA under this breeding program and that half of the
offspring of a plant of genotype Aa will be of genotype AA.
 So, according to the calculation of linear algebra we can see that
there have a few probabilities to occur autosomal recessive
inheritence.
12

13. Conclusion
 Possible way to control such a disease is for the breeder to always
mate a female, regardless of her genotype, with a normal male. In
this way, all future offspring will either have a normal father and a
normal mother (AA–AA matings) or a normal father and a carrier
mother (AA–Aa matings).
13

14. Thank You
14