More Related Content
PPT
Matemática Discreta - Introdução DOC
lista-de-exercicios-funcao-exponencial PDF
08 equação do primeiro grau DOC
1 exercícios de potenciação PPT
PDF
PDF
Respostas do-livro-geometria-analitica-alfredo-steinbruch-e-paulo-winterle PDF
Resolução comentada matemática 002 What's hot
PDF
Exercícios sobre m.m.c. e m.d.c. PDF
Lista (6) de exercícios de multiplicação e divisão PDF
11 sistema de inequação do primeiro grau PDF
3 exercicios potencia conm respostas - 9º ano PDF
PDF
Tabela de identidades trigonometricas DOC
Multiplicacao Divisao 7ano PDF
Mat produtos notaveis resolvidos PDF
Exercícios Resolvidos: Taxa relacionada PDF
DOC
Exercicios derivada lista3 PDF
PDF
Exercícios Resolvidos: Distribuição Binomial PPT
Aula 09 Medidas de Tendencia Central de Dados Agrupados PDF
Valores próprios e vetores próprios PPTX
PDF
Números inteiros relativos multiplicação e divisão PDF
34 nucleo e imagem de uma transformacao linear PDF
PDF
1ª lista de exercicios e lista de revisão 2ºbim 7º ano Viewers also liked
PDF
PPTX
PDF
Aula de Cálculo I - Limite PDF
Exercícios de calculo 1 limites PPTX
Função exponencial exercícios resolvidos PPTX
PPSX
Operacoes numeros decimais PDF
Exercicios-resolvidos-de-calculo-i (1) PPT
CentroApoio.com - Matemática - Função Exponencial - Vídeo Aulas PPT
Aula 01 limites e continuidade PDF
PPTX
PPT
Aula 02 Cálculo de limites - Conceitos Básicos PPTX
Revisão Enem - caderno Sartre Coc- Função do 1°grau - Função do 2° grau - Fun... DOC
Soma Diferenca Multiplicacao Divisao Decimais PDF
PPTX
Mat divisao aprender.compreender PDF
PPTX
Regras para o algoritmo da divisão 2 PDF
Álgebra Linear Para Leigos Similar to Limite lista 1
DOC
DOC
DOC
PDF
Μαθηματικά Προσανατολισμού Γ' Λυκείου - Όρια Α' PDF
Introducción a los límites con geogebra PDF
203 bai-tap-gioi-han-www.mathvn.com DOCX
PDF
DOCX
PDF
Persamaan dan Pertidaksamaan Nilai Mutlak PDF
PDF
PDF
Limite lista 1
- 1.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 1
Caro aluno, aprender exige esforço e perseverança. Grandes conquistas exige grandes esforços. Bons
estudos!
A resolução dos exercícios propostos demonstra a possibilidade de resolução apenas aplicando a
substituição do valor à qual o limite tende.
1. 𝑙𝑖𝑚
𝑥→2
(3𝑥2
− 5𝑥 + 2) =
Para resolver o limite, vamos substituir o "x" pelo 1.
𝑙𝑖𝑚
𝑥→2
(3 ∙ 22
− 5 ∙ 2 + 2) = 4
Observe o gráfico e verifique a resolução
∴ 𝒍𝒊𝒎
𝒙→𝟐
( 𝟑𝒙 𝟐
− 𝟓𝒙 + 𝟐) = 𝟒
__________________________________________________________________________________________
2. 𝑙𝑖𝑚
𝑥→−1
𝑥2
+ 2𝑥 − 3
4𝑥 − 3
= 𝑙𝑖𝑚
𝑥→−1
(−1)2
+ 2 ∙ (−1) − 3
4 ∙ (−1)− 3
=
−4
−7
=
4
7
∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 𝟐
+ 𝟐𝒙 − 𝟑
𝟒𝒙 − 𝟑
=
𝟒
𝟕
__________________________________________________________________________________________
3. 𝑙𝑖𝑚
𝑥→1
(
2𝑥2
− 𝑥 + 1
3𝑥 − 2
)
2
= 𝑙𝑖𝑚
𝑥→1
(
2 ∙ 12
− 1 + 1
3 ∙ 1 − 2
)
2
= 4 ∴ 𝒍𝒊𝒎
𝒙→𝟏
(
𝟐𝒙 𝟐
− 𝒙 + 𝟏
𝟑𝒙 − 𝟐
)
𝟐
= 𝟒
__________________________________________________________________________________________
4. 𝑙𝑖𝑚
𝑥→−2
√
𝑥3 + 2𝑥2 − 3𝑥 + 2
𝑥2 + 4𝑥 + 3
=
3
𝑙𝑖𝑚
𝑥→−2
√
(−2)3 + 2 ∙ (−2)2 − 3 ∙ (−2) + 2
(−2)2 + 4 ∙ (−2) + 3
= −2
3
∴ 𝒍𝒊𝒎
𝒙→−𝟐
√
𝒙 𝟑 + 𝟐𝒙 𝟐 − 𝟑𝒙 + 𝟐
𝒙 𝟐 + 𝟒𝒙 + 𝟑
= −𝟐
𝟑
__________________________________________________________________________________________
5. 𝑙𝑖𝑚
𝑥→1
4𝑥2
− 7𝑥 + 5 = 𝑙𝑖𝑚
𝑥→1
4 ∙ 12
− 7 ∙ 1 + 5 = 2 ∴ 𝒍𝒊𝒎
𝒙→𝟏
𝟒𝒙 𝟐
− 𝟕𝒙 + 𝟓 = 𝟐
__________________________________________________________________________________________
6. 𝑙𝑖𝑚
𝑥→−1
𝑥3
− 2𝑥2
− 4𝑥 + 3 = 𝑙𝑖𝑚
𝑥→−1
(−1)3
− 2 ∙ (−1)2
− 4 ∙ (−1) + 3 = 4
∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 𝟑
− 𝟐𝒙 𝟐
− 𝟒𝒙 + 𝟑 = 𝟒
- 2.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 2
__________________________________________________________________________________________
7. 𝑙𝑖𝑚
𝑥→2
3𝑥 + 2
𝑥2 − 6𝑥 + 5
= 𝑙𝑖𝑚
𝑥→2
3 ∙ 2 + 2
22 − 6 ∙ 2 + 5
= −
8
3
∴ 𝒍𝒊𝒎
𝒙→𝟐
𝟑𝒙 + 𝟐
𝒙 𝟐 − 𝟔𝒙 + 𝟓
= −
𝟖
𝟑
_________________________________________________________________________________________
8. 𝑙𝑖𝑚
𝑥→−1
𝑥2
− 5𝑥 + 4
2𝑥 + 1
= 𝑙𝑖𝑚
𝑥→−1
3 ∙ (−1)2
− 5 ∙ (−1)+ 4
2 ∙ (−1)+ 1
= 12 ∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 𝟐
− 𝟓𝒙 + 𝟒
𝟐𝒙 + 𝟏
= 𝟏𝟐
__________________________________________________________________________________________
9. 𝑙𝑖𝑚
𝑥→−3
𝑥2
+ 2𝑥 − 3
5 − 3𝑥
= 𝑙𝑖𝑚
𝑥→−3
(−3)2
+ 2 ∙ (−3) − 3
5 − 3 ∙ (−3)
=
0
14
= 0 ∴ 𝒍𝒊𝒎
𝒙→−𝟑
𝒙 𝟐
+ 𝟐𝒙 − 𝟑
𝟓 − 𝟑𝒙
= 𝟎
__________________________________________________________________________________________
10. 𝑙𝑖𝑚
𝑥→2
(
3𝑥2
− 2𝑥 − 5
−𝑥2 + 3𝑥 + 4
)
3
= 𝑙𝑖𝑚
𝑥→2
(
3 ∙ 22
− 2 ∙ 2 − 5
−22 + 3 ∙ 2 + 4
)
3
= (
3
6
)
3
= (
1
2
)
3
=
1
8
∴ 𝒍𝒊𝒎
𝒙→𝟐
(
𝟑𝒙 𝟐
− 𝟐𝒙 − 𝟓
−𝒙 𝟐 + 𝟑𝒙 + 𝟒
)
𝟑
=
𝟏
𝟖
__________________________________________________________________________________________
11. 𝑙𝑖𝑚
𝑥→4
(
𝑥3
− 3𝑥2
− 2𝑥 − 5
2𝑥2 − 9𝑥 + 2
)
2
= 𝑙𝑖𝑚
𝑥→4
(
43
− 3 ∙ 42
− 2 ∙ 4 − 5
2 ∙ 42 − 9 ∙ 4 + 2
)
2
= (
3
2
)
2
=
9
4
∴ 𝒍𝒊𝒎
𝒙→𝟒
(
𝒙 𝟑
− 𝟑𝒙 𝟐
− 𝟐𝒙 − 𝟓
𝟐𝒙 𝟐 − 𝟗𝒙 + 𝟐
)
𝟐
=
𝟗
𝟒
__________________________________________________________________________________________
12. 𝑙𝑖𝑚
𝑥→−1
√
2𝑥2 + 3𝑥 − 4
5𝑥 − 4
= 𝑙𝑖𝑚
𝑥→−1
√
2 ∙ (−1)2 + 3 ∙ (−1) − 4
5 ∙ (−1) − 4
= √
−5
−9
=
√5
3
∴ 𝒍𝒊𝒎
𝒙→−𝟏
√
𝟐𝒙 𝟐 + 𝟑𝒙 − 𝟒
𝟓𝒙 − 𝟒
=
√ 𝟓
𝟑
__________________________________________________________________________________________
13. lim
𝑥→−2
√
3𝑥3 − 5𝑥2 − 𝑥 + 2
4𝑥 + 3
3
= lim
𝑥→−2
√
3 ∙ (−2)3 − 5 ∙ (−2)2 − (−2) + 2
4(−2)+ 3
3
= √
−40
−5
3
= √8
3
= 2
- 3.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 3
∴ 𝒍𝒊𝒎
𝒙→−𝟐
√
𝟑𝒙 𝟑 − 𝟓𝒙 𝟐 − 𝒙 + 𝟐
𝟒𝒙 + 𝟑
𝟑
= 𝟐
__________________________________________________________________________________________
14. 𝑙𝑖𝑚
𝑥→2
√2𝑥2 + 3𝑥 + 2
6 − 4𝑥
= 𝑙𝑖𝑚
𝑥→2
√2 ∙ 22 + 3 ∙ 2 + 2
6 − 4 ∙ 2
=
4
−2
= −2
∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝟐𝒙 𝟐 + 𝟑𝒙 + 𝟐
𝟔 − 𝟒𝒙
= −𝟐
__________________________________________________________________________________________
15. lim
𝑥→2
𝑥2
− 4
𝑥2 − 2𝑥
= lim
𝑥→2
22
− 4
22 − 2 ∙ 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
𝑥2
− 4 = ( 𝑥 + 2)( 𝑥 − 2) 𝑒 𝑥2
− 2𝑥 = 𝑥(𝑥 − 2) , assim temos:
𝑙𝑖𝑚
𝑥→2
𝑥2
− 4
𝑥2 − 2𝑥
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(𝑥 − 2)
𝑥(𝑥 − 2)
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)
𝑥
= 𝑙𝑖𝑚
𝑥→2
(2 + 2)
2
= 2 ∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 𝟐
− 𝟒
𝒙 𝟐 − 𝟐𝒙
= 𝟐
__________________________________________________________________________________________
16. 𝑙𝑖𝑚
𝑥→1
𝑥2
− 1
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
12
− 1
1 − 1
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador.
𝑥2
− 1 = ( 𝑥 + 1)( 𝑥 − 1) , 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
𝑥2
− 1
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 + 1)(𝑥 − 1)
(𝑥 − 1)
= 𝑙𝑖𝑚
𝑥→1
(𝑥 + 1) = 2 ∴ 𝒍𝒊𝒎
𝒙→𝟏
𝒙 𝟐
− 𝟏
𝒙 − 𝟏
= 𝟐
__________________________________________________________________________________________
17. 𝑙𝑖𝑚
𝑥→−2
4 − 𝑥2
2 + 𝑥
= 𝑙𝑖𝑚
𝑥→−2
4 − (−2)2
2 + (−2)
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador.
4 − 𝑥2
= (2 + 𝑥)(2 − 𝑥)
- 4.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 4
𝑙𝑖𝑚
𝑥→−2
4 − 𝑥2
2 + 𝑥
= 𝑙𝑖𝑚
𝑥→−2
(2 + 𝑥)(2− 𝑥)
(2 + 𝑥)
= 𝑙𝑖𝑚
𝑥→−2
(2 + 2) = 4 ∴ 𝒍𝒊𝒎
𝒙→−𝟐
𝟒 − 𝒙 𝟐
𝟐 + 𝒙
= 𝟒
__________________________________________________________________________________________
18. 𝑙𝑖𝑚
𝑥→
3
2
4𝑥2
− 9
2𝑥 − 3
= 𝑙𝑖𝑚
𝑥→
3
2
4(
3
2
)
2
− 9
2 (
3
2
) − 3
= 𝑙𝑖𝑚
𝑥→
3
2
4 ∙
9
4
− 9
2 ∙
3
2
− 3
= 𝑙𝑖𝑚
𝑥→
3
2
9 − 9
3 − 3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador.
4𝑥2
− 9 = (2𝑥 + 3)(2𝑥 − 3) , 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→
3
2
4𝑥2
− 9
2𝑥 − 3
= 𝑙𝑖𝑚
𝑥→
3
2
(2𝑥 + 3)(2𝑥 − 3)
(2𝑥 − 3)
= 𝑙𝑖𝑚
𝑥→
3
2
(2 ∙
3
2
+ 3) = 6 ∴ 𝒍𝒊𝒎
𝒙→
𝟑
𝟐
𝟒𝒙 𝟐
− 𝟗
𝟐𝒙 − 𝟑
= 𝟔
__________________________________________________________________________________________
19. lim
𝑥→3
𝑥2
− 4𝑥 + 3
𝑥2 − 𝑥 − 6
= lim
𝑥→3
32
− 4 ∙ 3 + 3
32 − 3 − 6
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
𝑥2
− 4𝑥 + 3 = ( 𝑥 − 3)( 𝑥 − 1) 𝑒 𝑥2
− 𝑥 − 6 = (𝑥 − 3)(𝑥 + 2) , 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→3
𝑥2
− 4𝑥 + 3
𝑥2 − 𝑥 − 6
= 𝑙𝑖𝑚
𝑥→3
( 𝑥 − 3)( 𝑥 − 1)
(𝑥 − 3)(𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→3
( 𝑥 − 1)
(𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→3
(3 − 1)
(3 + 2)
=
2
5
∴ 𝒍𝒊𝒎
𝒙→𝟑
𝒙 𝟐
− 𝟒𝒙 + 𝟑
𝒙 𝟐 − 𝒙 − 𝟔
=
𝟐
𝟓
__________________________________________________________________________________________
20. 𝑙𝑖𝑚
𝑥→
1
2
2𝑥2
+ 5𝑥 − 3
2𝑥2 − 5𝑥 + 2
= 𝑙𝑖𝑚
𝑥→
1
2
2 ∙ (
1
2)
2
+ 5 ∙
1
2 − 3
2 ∙ (
1
2
)
2
− 5 ∙
1
2
+ 2
= 𝑙𝑖𝑚
𝑥→
1
2
2 ∙
1
4
+ 5 ∙
1
2
− 3
2 ∙
1
4
− 5 ∙
1
2
+ 2
=
= 𝑙𝑖𝑚
𝑥→
1
2
1
2
+
5
2
− 3
1
2
−
5
2
+ 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
- 5.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 5
2𝑥2
+ 5𝑥 − 3 = ( 𝑥 + 3)(𝑥 −
1
2
) 𝑒 2𝑥2
− 5𝑥 + 2 = ( 𝑥 − 2)(𝑥 −
1
2
) , 𝑒𝑛𝑡ã𝑜 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→
1
2
2𝑥2
+ 5𝑥 − 3
2𝑥2 − 5𝑥 + 2
= 𝑙𝑖𝑚
𝑥→
1
2
( 𝑥 + 3) (𝑥 −
1
2
)
( 𝑥 − 2) (𝑥 −
1
2
)
= 𝑙𝑖𝑚
𝑥→
1
2
( 𝑥 + 3)
( 𝑥 − 2)
= 𝑙𝑖𝑚
𝑥→
1
2
(
1
2
+ 3)
(
1
2
− 2)
=
= 𝑙𝑖𝑚
𝑥→
1
2
(
1
2
+ 3)
(
1
2
− 2)
= 𝑙𝑖𝑚
𝑥→
1
2
7
2
−
3
2
= −
14
6
= −
7
3
∴ 𝒍𝒊𝒎
𝒙 →
𝟏
𝟐
𝟐𝒙 𝟐
+ 𝟓𝒙 − 𝟑
𝟐𝒙 𝟐 − 𝟓𝒙 + 𝟐
= −
𝟕
𝟑
__________________________________________________________________________________________
21. lim
𝑥→−
3
2
6𝑥2
+ 11𝑥 + 3
2𝑥2 − 5𝑥 − 12
= lim
𝑥→−
3
2
6 ∙ (−
3
2
)
2
+ 11 ∙ (−
3
2
) + 3
2 ∙ (−
3
2
)
2
− 5 ∙ (−
3
2
) − 12
= lim
𝑥→−
3
2
6 ∙
9
4
−
33
2
+ 3
2 ∙
9
4
+
15
2
− 12
=
= lim
𝑥→−
3
2
27
2
−
33
2
+ 3
9
2
+
15
2
− 12
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
6𝑥2
+ 11𝑥 + 3 = (3𝑥 + 1)(2𝑥 + 3) 𝑒 2𝑥2
− 5𝑥 − 12 = ( 𝑥 − 4)(2𝑥 + 3), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→−
3
2
6𝑥2
+ 11𝑥 + 3
2𝑥2 − 5𝑥 − 12
= 𝑙𝑖𝑚
𝑥→−
3
2
(3𝑥 + 1)(2𝑥 + 3)
( 𝑥 − 4)(2𝑥 + 3)
= 𝑙𝑖𝑚
𝑥→−
3
2
(3𝑥 + 1)
( 𝑥 − 4)
=
= 𝑙𝑖𝑚
𝑥→−
3
2
3 ∙ (−
3
2
) + 1
−
3
2
− 4
= 𝑙𝑖𝑚
𝑥→−
3
2
−
9
2
+ 1
−
3
2
− 4
=
−
7
2
−
11
2
=
14
22
=
7
11
∴ 𝒍𝒊𝒎
𝒙→−
𝟑
𝟐
𝟔𝒙 𝟐
+ 𝟏𝟏𝒙 + 𝟑
𝟐𝒙 𝟐 − 𝟓𝒙 − 𝟏𝟐
=
𝟕
𝟏𝟏
__________________________________________________________________________________________
22. 𝑙𝑖𝑚
𝑥→1
𝑥3
− 1
𝑥2 − 1
= 𝑙𝑖𝑚
𝑥→1
13
− 1
12 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
𝑥3
− 1 = ( 𝑥 − 1)( 𝑥2
+ 𝑥 + 1) 𝑒 𝑥2
− 1 = ( 𝑥 + 1)( 𝑥 − 1), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
𝑥3
− 1
𝑥2 − 1
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)( 𝑥2
+ 𝑥 + 1)
( 𝑥 + 1)( 𝑥 − 1)
= 𝑙𝑖𝑚
𝑥→1
( 𝑥2
+ 𝑥 + 1)
( 𝑥 + 1)
=
= 𝑙𝑖𝑚
𝑥→1
12
+ 1 + 1
1 + 1
=
3
2
∴ 𝒍𝒊𝒎
𝒙→𝟏
𝒙 𝟑
− 𝟏
𝒙 𝟐 − 𝟏
=
𝟑
𝟐
- 6.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 6
__________________________________________________________________________________________
23. lim
𝑥→−2
8 + 𝑥3
4 − 𝑥2
= lim
𝑥→−2
8 + (−2)3
4 − (−2)2
= lim
𝑥→−2
8 − 8
4 − 4
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
8 + 𝑥3
= (2 + 𝑥)(4 − 2𝑥 + 𝑥2) 𝑒 4 − 𝑥2
= (2 + 𝑥)(2 − 𝑥) , 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
lim
𝑥→−2
8 + 𝑥3
4 − 𝑥2
= lim
𝑥→−2
(2 + 𝑥)(4− 2𝑥 + 𝑥2
)
(2 + 𝑥)(2 − 𝑥)
= lim
𝑥→−2
(4 − 2𝑥 + 𝑥2
)
(2 − 𝑥)
=
= 𝑙𝑖𝑚
𝑥→−2
4 − 2 ∙ (−2) + (−2)2
2 − (−2)
= 3 ∴ 𝒍𝒊𝒎
𝒙→−𝟐
𝟖 + 𝒙 𝟑
𝟒 − 𝒙 𝟐
= 𝟑
__________________________________________________________________________________________
24. 𝑙𝑖𝑚
𝑥→2
𝑥4
− 16
8 − 𝑥3
= 𝑙𝑖𝑚
𝑥→2
24
− 16
8 − 23
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador.
𝑥4
− 16 = ( 𝑥2
+ 4)( 𝑥 + 2)( 𝑥 − 2) 𝑒 8 − 𝑥3
= (2 − 𝑥)(4 + 2𝑥 + 𝑥2) , 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→2
𝑥4
− 16
8 − 𝑥3
= 𝑙𝑖𝑚
𝑥→2
( 𝑥2
+ 4)( 𝑥 + 2)( 𝑥 − 2)
−( 𝑥 − 2)(4 + 2𝑥 + 𝑥2)
= 𝑙𝑖𝑚
𝑥→2
−
( 𝑥2
+ 4)( 𝑥 + 2)
(4 + 2𝑥 + 𝑥2)
=
= 𝑙𝑖𝑚
𝑥→2
−
(22
+ 4)(2 + 2)
(4 + 2 ∙ 2 + 2)
= −
32
12
= −
8
3
∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 𝟒
− 𝟏𝟔
𝟖 − 𝒙 𝟑
= −
𝟖
𝟑
__________________________________________________________________________________________
25. 𝑙𝑖𝑚
𝑥→1
𝑥2
− 3𝑥 + 2
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
12
− 3 ∙ 1 + 2
1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador.
𝑥2
− 3𝑥 + 2 = ( 𝑥 − 2)(𝑥 − 1), assim temos:
𝑙𝑖𝑚
𝑥→1
𝑥2
− 3𝑥 + 2
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 2)(𝑥 − 1)
(𝑥 − 1)
= 𝑙𝑖𝑚
𝑥→1
1 − 2 = −1 ∴ 𝒍𝒊𝒎
𝒙→𝟏
𝒙 𝟐
− 𝟑𝒙 + 𝟐
𝒙 − 𝟏
= −𝟏
__________________________________________________________________________________________
- 7.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 7
26. 𝑙𝑖𝑚
𝑥→1
2𝑥3
+ 𝑥2
− 4𝑥 + 1
𝑥3 − 3𝑥2 + 5𝑥 − 3
= 𝑙𝑖𝑚
𝑥→1
2 ∙ (1)3
+ 12
− 4 ∙ 1 + 1
13 − 3 ∙ (1)2 + 5 ∙ 1 − 3
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini. Veja a demonstração no site em Aulas Slides - Fatoração e Produtos Notáveis.
2𝑥3
+ 𝑥2
− 4𝑥 + 1 = ( 𝑥 − 1)(2𝑥2
+ 3𝑥 − 1)
𝑥3
− 3𝑥2
+ 5𝑥 − 3 = ( 𝑥 − 1)( 𝑥2
− 2𝑥 + 3), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
2𝑥3
+ 𝑥2
− 4𝑥 + 1
𝑥3 − 3𝑥2 + 5𝑥 − 3
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)(2𝑥2
+ 3𝑥 − 1)
( 𝑥 − 1)( 𝑥2 − 2𝑥 + 3)
= 𝑙𝑖𝑚
𝑥→1
(2𝑥2
+ 3𝑥 − 1)
( 𝑥2 − 2𝑥 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
2 ∙ (1)2
+ 3 ∙ (1) − 1
(1)2 − 2 ∙ (1)+ 3
=
4
2
= 2 ∴ 𝒍𝒊𝒎
𝒙→𝟏
𝟐𝒙 𝟑
+ 𝒙 𝟐
− 𝟒𝒙 + 𝟏
𝒙 𝟑 − 𝟑𝒙 𝟐 + 𝟓𝒙 − 𝟑
= 𝟐
__________________________________________________________________________________________
27. 𝑙𝑖𝑚
𝑥→−1
𝑥3
+ 3𝑥2
− 𝑥 − 3
𝑥3 − 𝑥2 + 2
= 𝑙𝑖𝑚
𝑥→−1
(−1)3
+ 3(−1)2
− (−1)− 3
(−1)− (−1)2 + 2
=
= 𝑙𝑖𝑚
𝑥→−1
(−1)3
+ 3(−1)2
− (−1) − 3
(−1) − (−1)2 + 2
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥3
+ 3𝑥2
− 𝑥 − 3 = ( 𝑥 + 1)(𝑥2
+ 2𝑥 − 3)
𝑥3
− 𝑥2
+ 2 = ( 𝑥 + 1)(𝑥2
− 2𝑥 + 2), assim temos:
𝑙𝑖𝑚
𝑥→−1
𝑥3
+ 3𝑥2
− 𝑥 − 3
𝑥3 − 𝑥2 + 2
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1)(𝑥2
+ 2𝑥 − 3)
( 𝑥 + 1)(𝑥2 − 2𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→−1
𝑥2
+ 2𝑥 − 3
𝑥2 − 2𝑥 + 2
=
= 𝑙𝑖𝑚
𝑥→−1
(−1)2
+ 2 ∙ (−1)− 3
(−1)2 − 2 ∙ (−1)+ 2
= −
4
5
∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 𝟑
+ 𝟑𝒙 𝟐
− 𝒙 − 𝟑
𝒙 𝟑 − 𝒙 𝟐 + 𝟐
= −
𝟒
𝟓
__________________________________________________________________________________________
- 8.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 8
28. 𝑙𝑖𝑚
𝑥→3
𝑥3
− 6𝑥 − 9
𝑥3 − 8𝑥 − 3
= 𝑙𝑖𝑚
𝑥→3
33
− 6 ∙ 3 − 9
33 − 8 ∙ 3 − 3
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥3
− 6𝑥 − 9 = ( 𝑥 − 3)(𝑥2
+ 3𝑥 + 3)
𝑥3
− 8𝑥 − 3 = ( 𝑥 − 3)(𝑥2
+ 3𝑥 + 1) , assim temos:
𝑙𝑖𝑚
𝑥→3
𝑥3
− 6𝑥 − 9
𝑥3 − 8𝑥 − 3
= 𝑙𝑖𝑚
𝑥→3
( 𝑥 − 3)(𝑥2
+ 3𝑥 + 3)
( 𝑥 − 3)(𝑥2 + 3𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→3
𝑥2
+ 3𝑥 + 3
𝑥2 + 3𝑥 + 1
=
= 𝑙𝑖𝑚
𝑥→3
32
+ 3 ∙ 3 + 3
32 + 3 ∙ 3 + 1
=
21
19
∴ 𝒍𝒊𝒎
𝒙→𝟑
𝒙 𝟑
− 𝟔𝒙 − 𝟗
𝒙 𝟑 − 𝟖𝒙 − 𝟑
=
𝟐𝟏
𝟏𝟗
__________________________________________________________________________________________
29. 𝑙𝑖𝑚
𝑥→1
𝑥3
− 3𝑥2
+ 6𝑥 − 4
𝑥3 − 4𝑥2 + 8𝑥 − 5
= 𝑙𝑖𝑚
𝑥→1
13
− 3 ∙ 12
+ 6 ∙ 1 − 4
13 − 4 ∙ 12 + 8 ∙ 1 − 5
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥3
− 3𝑥2
+ 6𝑥 − 4 = ( 𝑥 − 1)(𝑥2
− 2𝑥 + 4)
𝑥3
− 4𝑥2
+ 8𝑥 − 5 = ( 𝑥 − 1)(𝑥2
− 3𝑥 + 5)
𝑙𝑖𝑚
𝑥→1
𝑥3
− 3𝑥2
+ 6𝑥 − 4
𝑥3 − 4𝑥2 + 8𝑥 − 5
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)(𝑥2
− 2𝑥 + 4)
( 𝑥 − 1)(𝑥2 − 3𝑥 + 5)
= 𝑙𝑖𝑚
𝑥→1
(𝑥2
− 2𝑥 + 4)
(𝑥2 − 3𝑥 + 5)
=
= 𝑙𝑖𝑚
𝑥→1
12
− 2 ∙ 1 + 4
12 − 3 ∙ 1 + 5
=
3
3
= 1 ∴ 𝒍𝒊𝒎
𝒙→𝟏
𝒙 𝟑
− 𝟑𝒙 𝟐
+ 𝟔𝒙 − 𝟒
𝒙 𝟑 − 𝟒𝒙 𝟐 + 𝟖𝒙 − 𝟓
= 𝟏
__________________________________________________________________________________________
30. 𝑙𝑖𝑚
𝑥→2
𝑥4
− 10𝑥 + 4
𝑥3 − 2𝑥2
= 𝑙𝑖𝑚
𝑥→2
24
− 10 ∙ 2 + 4
23 − 2 ∙ 22
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥4
− 10𝑥 + 4 = ( 𝑥 − 2)(𝑥3
+ 2𝑥2
+ 4𝑥 − 2)
𝑥3
− 2𝑥2
= ( 𝑥 − 2) 𝑥2
, assim temos:
- 9.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 9
𝑙𝑖𝑚
𝑥→2
𝑥4
− 10𝑥 + 4
𝑥3 − 2𝑥2
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 − 2)(𝑥3
+ 2𝑥2
+ 4𝑥 − 2)
( 𝑥 − 2) 𝑥2
= 𝑙𝑖𝑚
𝑥→2
𝑥3
+ 2𝑥2
+ 4𝑥 − 2
𝑥2
=
= 𝑙𝑖𝑚
𝑥→2
23
+ 2 ∙ 22
+ 4 ∙ 2 − 2
22
=
22
4
=
11
2
∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 𝟒
− 𝟏𝟎𝒙 + 𝟒
𝒙 𝟑 − 𝟐𝒙 𝟐
=
𝟏𝟏
𝟐
__________________________________________________________________________________________
31. 𝑙𝑖𝑚
𝑥→1
3𝑥3
− 4𝑥2
− 𝑥 + 2
2𝑥3 − 3𝑥2 + 1
= 𝑙𝑖𝑚
𝑥→1
3 ∙ (1)3
− 4 ∙ (1)2
− 1 + 2
2 ∙ (1)2 − 3 ∙ (1)2 + 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
3𝑥3
− 4𝑥2
− 𝑥 + 2 = ( 𝑥 − 1)(3𝑥2
− 𝑥 − 2)
2𝑥3
− 3𝑥2
+ 1 = ( 𝑥 − 1)(2𝑥2
− 𝑥 − 1), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
3𝑥3
− 4𝑥2
− 𝑥 + 2
2𝑥3 − 3𝑥2 + 1
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)(3𝑥2
− 𝑥 − 2)
( 𝑥 − 1)(2𝑥2 − 𝑥 − 1)
= 𝑙𝑖𝑚
𝑥→1
3𝑥2
− 𝑥 − 2
2𝑥2 − 𝑥 − 1
=
= 𝑙𝑖𝑚
𝑥→1
3 ∙ (1)2
− 1 − 2
2 ∙ (1)2 − 1 − 1
=
0
0
(𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑎𝑚𝑜𝑠 𝑐𝑜𝑚 𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Vamos fazer novamente a fatoração utilizando Bhaskara.
3𝑥2
− 𝑥 − 2 = ( 𝑥 − 1)(3𝑥 + 2) 𝑒 2𝑥2
− 𝑥 − 1 = ( 𝑥 − 1)(2𝑥 + 1), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
3𝑥2
− 𝑥 − 2
2𝑥2 − 𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)(3𝑥 + 2)
( 𝑥 − 1)(2𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→1
3𝑥 + 2
2𝑥 + 1
=
= 𝑙𝑖𝑚
𝑥→1
3 ∙ 1 + 2
2 ∙ 1 + 1
=
5
3
∴ 𝒍𝒊𝒎
𝒙→𝟏
𝟑𝒙 𝟑
− 𝟒𝒙 𝟐
− 𝒙 + 𝟐
𝟐𝒙 𝟑 − 𝟑𝒙 𝟐 + 𝟏
=
𝟓
𝟑
__________________________________________________________________________________________
32. 𝑙𝑖𝑚
𝑥→1
𝑥3
− 3𝑥 + 2
𝑥4 − 4𝑥 + 3
= 𝑙𝑖𝑚
𝑥→1
(1)3
− 3 ∙ (1) + 2
(1)4 − 4 ∙ (1) + 3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥3
− 3𝑥 + 2 = ( 𝑥 − 1)( 𝑥2
+ 𝑥 − 2) 𝑒 𝑥4
− 4𝑥 + 3 = ( 𝑥 − 1)( 𝑥3
+ 𝑥2
+ 𝑥 − 3), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
𝑥3
− 3𝑥 + 2
𝑥4 − 4𝑥 + 3
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)( 𝑥2
+ 𝑥 − 2)
( 𝑥 − 1)( 𝑥3 + 𝑥2 + 𝑥 − 3)
= 𝑙𝑖𝑚
𝑥→1
𝑥2
+ 𝑥 − 2
𝑥3 + 𝑥2 + 𝑥 − 3
=
= 𝑙𝑖𝑚
𝑥→1
(1)2
+ 1 − 2
(1)3 + (1)2 + 1 − 3
=
0
0
(𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑎𝑚𝑜𝑠 𝑐𝑜𝑚 𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
- 10.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 10
Vamos fazer novamente a fatoração utilizando Bhaskara.
𝑥2
+ 𝑥 − 2 = ( 𝑥 − 1)( 𝑥 + 2) 𝑒 𝑥3
+ 𝑥2
+ 𝑥 − 3 = ( 𝑥 − 1)( 𝑥2
+ 2𝑥 + 3), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→1
𝑥2
+ 𝑥 − 2
𝑥3 + 𝑥2 + 𝑥 − 3
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)( 𝑥 + 2)
( 𝑥 − 1)( 𝑥2 + 2𝑥 + 3)
= 𝑙𝑖𝑚
𝑥→1
𝑥 + 2
𝑥2 + 2𝑥 + 3
=
= 𝑙𝑖𝑚
𝑥→1
1 + 2
12 + 2 ∙ 1 + 3
=
3
6
=
1
2
∴ 𝒍𝒊𝒎
𝒙→𝟏
𝒙 𝟑
− 𝟑𝒙 + 𝟐
𝒙 𝟒 − 𝟒𝒙 + 𝟑
=
𝟏
𝟐
__________________________________________________________________________________________
33. 𝑙𝑖𝑚
𝑥→−2
𝑥4
+ 4𝑥3
+ 𝑥2
− 12𝑥 − 12
2𝑥3 + 7𝑥2 + 4𝑥 − 4
= 𝑙𝑖𝑚
𝑥→−2
(−2)4
+ 4 ∙ (−2)3
+ (−2)2
− 12 ∙ (−2)− 12
2 ∙ (−2)3 + 7 ∙ (−2)2 + 4 ∙ (−2) − 4
=
= 𝑙𝑖𝑚
𝑥→−2
16 − 32 + 4 + 24 − 12
−16 + 28 − 8 − 4
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥4
+ 4𝑥3
+ 𝑥2
− 12𝑥 − 12 = ( 𝑥 + 2)(𝑥3
+ 2𝑥2
− 3𝑥 − 6)
2𝑥3
+ 7𝑥2
+ 4𝑥 − 4 = ( 𝑥 + 2)(2𝑥2
+ 3𝑥 − 2), 𝑎𝑠𝑠𝑖𝑚 𝑡𝑒𝑚𝑜𝑠:
𝑙𝑖𝑚
𝑥→−2
𝑥4
+ 4𝑥3
+ 𝑥2
− 12𝑥 − 12
2𝑥3 + 7𝑥2 + 4𝑥 − 4
= 𝑙𝑖𝑚
𝑥→−2
( 𝑥 + 2)(𝑥3
+ 2𝑥2
− 3𝑥 − 6)
( 𝑥 + 2)(2𝑥2 + 3𝑥 − 2)
= 𝑙𝑖𝑚
𝑥→−2
(𝑥3
+ 2𝑥2
− 3𝑥 − 6)
(2𝑥2 + 3𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→−2
(−2)3
+ 2 ∙ (−2)2
− 3 ∙ (−2) − 6
2 ∙ (−2)2 + 3 ∙ (−2)− 2
=
0
0
(𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑎𝑚𝑜𝑠 𝑐𝑜𝑚 𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Vamos fazer novamente a fatoração utilizando o Dispositivo de Briot-Ruffini e Bhaskara.
𝑥3
+ 2𝑥2
− 3𝑥 − 6 = ( 𝑥 + 2)(𝑥2
− 3)
2𝑥2
+ 3𝑥 − 2 = ( 𝑥 + 2)(2𝑥 − 1) , assim temos:
𝑙𝑖𝑚
𝑥→−2
(𝑥3
+ 2𝑥2
− 3𝑥 − 6)
(2𝑥2 + 3𝑥 − 2)
= 𝑙𝑖𝑚
𝑥→−2
( 𝑥 + 2)(𝑥2
− 3)
( 𝑥 + 2)(2𝑥 − 1)
= 𝑙𝑖𝑚
𝑥→−2
(𝑥2
− 3)
(2𝑥 − 1)
=
= 𝑙𝑖𝑚
𝑥→−2
𝑥2
− 3
2𝑥 − 1
= 𝑙𝑖𝑚
𝑥→−2
(−2)2
− 3
2 ∙ (−2) − 1
= −
1
5
∴ 𝒍𝒊𝒎
𝒙→−𝟐
𝒙 𝟒
+ 𝟒𝒙 𝟑
+ 𝒙 𝟐
− 𝟏𝟐𝒙 − 𝟏𝟐
𝟐𝒙 𝟑 + 𝟕𝒙 𝟐 + 𝟒𝒙 − 𝟒
= −
𝟏
𝟓
__________________________________________________________________________________________
34. 𝑙𝑖𝑚
𝑥→−1
𝑥4
− 𝑥3
− 𝑥2
+ 5𝑥 + 4
𝑥3 + 4𝑥2 + 5𝑥 + 2
= 𝑙𝑖𝑚
𝑥→−1
(−1)4
− (−1)3
− (−1)2
+ 5 ∙ (−1) + 4
(−1)3 + 4 ∙ (−1)2 + 5 ∙ (−1) + 2
=
- 11.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 11
𝑙𝑖𝑚
𝑥→−1
1 + 1 − 1 − 5 + 4
−1 + 4 − 5 + 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
Vamos efetuar as fatorações e fazer a verificação, onde pode ser notado a necessidade de efetuar novamente
a fatoração.
Numerador:
𝑥4
− 𝑥3
− 𝑥2
+ 5𝑥 + 4 = ( 𝑥 + 1)(𝑥3
− 2𝑥2
+ 𝑥 + 4), se substituirmos x= - 1, notaremos que o polinômio
terá como valor zero, assim há a necessidade de nova fatoração.
𝑥3
− 2𝑥2
+ 𝑥 + 4 = ( 𝑥 + 1)(𝑥2
− 3𝑥 + 4) , se substituirmos x= - 1, notaremos que o polinômio terá como
solução um número diferente de zero.
Sendo assim nosso polinômio fatorado resulta:
𝑥4
− 𝑥3
− 𝑥2
+ 5𝑥 + 4 = ( 𝒙 + 𝟏)(𝒙 + 𝟏)(𝒙 𝟐
− 𝟑𝒙 + 𝟒)
Denominador: (repetir o processo)
𝑥3
+ 4𝑥2
+ 5𝑥 + 2 = ( 𝒙 + 𝟏)( 𝒙+ 𝟏)( 𝒙 + 𝟐)
Como chegamos à simplificação final, vamos resolver o limite.
𝑙𝑖𝑚
𝑥→−1
𝑥4
− 𝑥3
− 𝑥2
+ 5𝑥 + 4
𝑥3 + 4𝑥2 + 5𝑥 + 2
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1)(𝑥 + 1)(𝑥2
− 3𝑥 + 4)
( 𝑥 + 1)( 𝑥 + 1)( 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→−1
(𝑥2
− 3𝑥 + 4)
( 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→−1
(−1)2
− 3(−1) + 4
−1 + 2
=
8
1
∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 𝟒
− 𝒙 𝟑
− 𝒙 𝟐
+ 𝟓𝒙 + 𝟒
𝒙 𝟑 + 𝟒𝒙 𝟐 + 𝟓𝒙 + 𝟐
= 𝟖
Caro aluno, quero deixar claro que existe outras formas de resolução, cabe a você efetuar pesquisas para
melhorar seu entendimento.
35. 𝑙𝑖𝑚
𝑥→−2
𝑥4
+ 2𝑥3
− 5𝑥2
− 12𝑥 − 4
2𝑥4 + 7𝑥3 + 2𝑥2 − 12𝑥 − 8
= 𝑙𝑖𝑚
𝑥→−2
(−2)4
+ 2 ∙ (−2)3
− 5(−2)2
− 12 ∙ (−2)− 4
2 ∙ (−2)4 + 7 ∙ (−2)3 + 2 ∙ (−2)2 − 12 ∙ (−2) − 8
=
= 𝑙𝑖𝑚
𝑥→−2
16 − 16 − 20 + 24 − 4
32 − 56 + 8 + 24 − 8
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
- 12.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 12
Para resolver este limite temos que fatorar o numerador e o denominador, utilizaremos o Dispositivo de Briot-
Ruffini.
𝑥4
+ 2𝑥3
− 5𝑥2
− 12𝑥 − 4 = ( 𝑥 + 2)( 𝑥 + 2)(𝑥2
− 2𝑥 − 1)
2𝑥4
+ 7𝑥3
+ 2𝑥2
− 12𝑥 − 8 = ( 𝑥 + 2)( 𝑥 + 2)(2𝑥2
− 𝑥 − 2)
𝑙𝑖𝑚
𝑥→−2
𝑥4
+ 2𝑥3
− 5𝑥2
− 12𝑥 − 4
2𝑥4 + 7𝑥3 + 2𝑥2 − 12𝑥 − 8
= 𝑙𝑖𝑚
𝑥→−2
( 𝑥 + 2)( 𝑥 + 2)(𝑥2
− 2𝑥 − 1)
( 𝑥 + 2)( 𝑥 + 2)(2𝑥2 − 𝑥 − 2)
= 𝑙𝑖𝑚
𝑥→−2
(𝑥2
− 2𝑥 − 1)
(2𝑥2 − 𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→−2
(−2)2
− 2(−2) − 1
2(−2)2 − (−2) − 2
=
7
8
∴ 𝒍𝒊𝒎
𝒙→−𝟐
𝒙 𝟒
+ 𝟐𝒙 𝟑
− 𝟓𝒙 𝟐
− 𝟏𝟐𝒙 − 𝟒
𝟐𝒙 𝟒 + 𝟕𝒙 𝟑 + 𝟐𝒙 𝟐 − 𝟏𝟐𝒙 − 𝟖
=
𝟕
𝟖
______________________________________________________________________________________
Digite a equação aqui.____
36. 𝑙𝑖𝑚
𝑥→3
√1 + 𝑥 − 2
𝑥 − 3
= 𝑙𝑖𝑚
𝑥→3
√1 + 3 − 2
3 − 3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→3
√1 + 𝑥 − 2
𝑥 − 3
= 𝑙𝑖𝑚
𝑥→3
(√1+ 𝑥 − 2)(√1+ 𝑥 + 2)
( 𝑥 − 3)(√1 + 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→3
(√1 + 𝑥)2
− 22
( 𝑥 − 3)(√1+ 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→3
1 + 𝑥 − 4
( 𝑥 − 3)(√1 + 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→3
(𝑥 − 3)
( 𝑥 − 3)(√1 + 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→3
1
(√1+ 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→3
1
(√1+ 3 + 2)
=
1
4
∴ 𝒍𝒊𝒎
𝒙→𝟑
√ 𝟏 + 𝒙 − 𝟐
𝒙 − 𝟑
=
𝟏
𝟒
__________________________________________________________________________________________
37. 𝑙𝑖𝑚
𝑥→1
√ 𝑥 − 1
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
√1 − 1
1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√ 𝑥 − 1
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
(√ 𝑥 − 1)(√ 𝑥 + 1)
(𝑥 − 1)(√ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→1
(√ 𝑥)
2
− 12
(𝑥 − 1)(√ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→1
(𝑥 − 1)
(𝑥 − 1)(√ 𝑥 + 1)
=
𝑙𝑖𝑚
𝑥→1
1
(√ 𝑥 + 1)
=
1
2
∴ 𝒍𝒊𝒎
𝒙→𝟏
√ 𝒙 − 𝟏
𝒙 − 𝟏
=
𝟏
𝟐
38. 𝑙𝑖𝑚
𝑥→0
1 − √1 − 𝑥
𝑥
= 𝑙𝑖𝑚
𝑥→0
1 − √1 − 0
0
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
= 𝑙𝑖𝑚
𝑥→0
1 − √1 − 𝑥
𝑥
= 𝑙𝑖𝑚
𝑥→0
(1 − √1 − 𝑥)(1 + √1 − 𝑥)
𝑥(1 + √1 − 𝑥)
= 𝑙𝑖𝑚
𝑥→0
12
− (√1+ 𝑥)
2
𝑥(1 + √1 + 𝑥)
=
- 13.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 13
= 𝑙𝑖𝑚
𝑥→0
1 − 1 + 𝑥
𝑥(1 + √1 + 𝑥)
= = 𝑙𝑖𝑚
𝑥→0
𝑥
𝑥(1 + √1 + 𝑥)
= 𝑙𝑖𝑚
𝑥→0
1
(1 + √1 + 𝑥)
=
= 𝑙𝑖𝑚
𝑥→0
1
(1 + √1 + 0)
=
1
2
∴ 𝒍𝒊𝒎
𝒙→𝟎
𝟏 − √ 𝟏 − 𝒙
𝒙
=
𝟏
𝟐
__________________________________________________________________________________________
39. 𝑙𝑖𝑚
𝑥→1
√ 𝑥 + 3 − 2
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
√1 + 3 − 2
1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√ 𝑥 + 3 − 2
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
(√ 𝑥 + 3 − 2)(√ 𝑥 + 3 + 2)
(𝑥 − 1)(√ 𝑥 + 3 + 2)
= 𝑙𝑖𝑚
𝑥→1
(√ 𝑥 + 3)
2
− 22
(𝑥 − 1)(√ 𝑥 + 3 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
𝑥 + 3 − 4
(𝑥 − 1)(√ 𝑥 + 3 + 2)
= 𝑙𝑖𝑚
𝑥→1
(𝑥 − 1)
(𝑥 − 1)(√ 𝑥 + 3 + 2)
= 𝑙𝑖𝑚
𝑥→1
1
(√ 𝑥 + 3 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
1
(√1 + 3 + 2)
=
1
4
∴ 𝒍𝒊𝒎
𝒙→𝟏
√ 𝒙 + 𝟑 − 𝟐
𝒙 − 𝟏
=
𝟏
𝟒
__________________________________________________________________________________________
40. 𝑙𝑖𝑚
𝑥→0
√1 − 2𝑥 − 𝑥2 − 1
𝑥
= 𝑙𝑖𝑚
𝑥→0
√1 − 2 ∙ 0 − 02 − 1
0
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→0
√1 − 2𝑥 − 𝑥2 − 1
𝑥
= 𝑙𝑖𝑚
𝑥→0
(√1 − 2𝑥 − 𝑥2 − 1)(√1− 2𝑥 − 𝑥2 + 1)
𝑥(√1− 2𝑥 − 𝑥2 + 1)
= 𝑙𝑖𝑚
𝑥→0
(√1 − 2𝑥 − 𝑥2)
2
− 12
𝑥(√1− 2𝑥 − 𝑥2 + 1)
=
= 𝑙𝑖𝑚
𝑥→0
1 − 2𝑥 − 𝑥2
− 1
𝑥(√1 − 2𝑥 − 𝑥2 + 1)
= 𝑙𝑖𝑚
𝑥→0
−2𝑥 − 𝑥2
𝑥(√1− 2𝑥 − 𝑥2 + 1)
= 𝑙𝑖𝑚
𝑥→0
𝑥(−2 − 𝑥)
𝑥(√1− 2𝑥 − 𝑥2 + 1)
=
= 𝑙𝑖𝑚
𝑥→0
(−2 − 𝑥)
(√1 − 2𝑥 − 𝑥2 + 1)
= 𝑙𝑖𝑚
𝑥→0
(−2 − 0)
(√1− 2 ∙ 0 − 0 + 1)
= −
2
2
= −1 ∴ 𝒍𝒊𝒎
𝒙→𝟎
√𝟏 − 𝟐𝒙 − 𝒙 𝟐 − 𝟏
𝒙
= − 𝟏
__________________________________________________________________________________________
41. 𝑙𝑖𝑚
𝑥→0
√1 + 𝑥 − √1 − 𝑥
𝑥
= 𝑙𝑖𝑚
𝑥→0
√1 + 0 − √1 − 0
0
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→0
√1 + 𝑥 − √1 − 𝑥
𝑥
= 𝑙𝑖𝑚
𝑥→0
(√1+ 𝑥 − √1 − 𝑥)(√1 + 𝑥 + √1 − 𝑥)
𝑥(√1+ 𝑥 + √1 − 𝑥)
= 𝑙𝑖𝑚
𝑥→0
(√1 + 𝑥)
2
− (√1 − 𝑥)
2
𝑥(√1+ 𝑥 + √1 − 𝑥)
=
- 14.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 14
= 𝑙𝑖𝑚
𝑥→0
1 + 𝑥 − (1 − 𝑥)
𝑥(√1 + 𝑥 + √1− 𝑥)
= 𝑙𝑖𝑚
𝑥→0
1 + 𝑥 − 1 + 𝑥
𝑥(√1+ 𝑥 + √1 − 𝑥)
= 𝑙𝑖𝑚
𝑥→0
2𝑥
𝑥(√1 + 𝑥 + √1 − 𝑥)
=
= 𝑙𝑖𝑚
𝑥→0
2 ∙ 𝑥
𝑥(√1 + 𝑥 + √1− 𝑥)
= 𝑙𝑖𝑚
𝑥→0
2
(√1+ 0 + √1 − 0)
=
2
2
= 1 ∴ 𝒍𝒊𝒎
𝒙→𝟎
√ 𝟏 + 𝒙 − √ 𝟏 − 𝒙
𝒙
= 𝟏
__________________________________________________________________________________________
42. 𝑙𝑖𝑚
𝑥→1
√2𝑥 − √ 𝑥 + 1
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
√2 ∙ 1 − √1 + 1
1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√2𝑥 − √ 𝑥 + 1
𝑥 − 1
= 𝑙𝑖𝑚
𝑥→1
(√2𝑥 − √ 𝑥 + 1)(√2𝑥 + √ 𝑥 + 1)
(𝑥 − 1)(√2𝑥 + √ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→1
(√2𝑥)
2
− (√ 𝑥 + 1)
2
(𝑥 − 1)(√2𝑥 + √ 𝑥 + 1)
=
= 𝑙𝑖𝑚
𝑥→1
2𝑥 − (𝑥 + 1)
(𝑥 − 1)(√2𝑥 + √ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→1
2𝑥 − 𝑥 − 1
(𝑥 − 1)(√2𝑥 + √ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→1
(𝑥 − 1)
(𝑥 − 1)(√2𝑥 + √ 𝑥 + 1)
=
= 𝑙𝑖𝑚
𝑥→1
1
(√2 ∙ 1 + √1 + 1)
=
1
2√2
=
√2
4
∴ 𝒍𝒊𝒎
𝒙→𝟏
√ 𝟐𝒙 − √ 𝒙 + 𝟏
𝒙 − 𝟏
=
√ 𝟐
𝟒
__________________________________________________________________________________________
43. 𝑙𝑖𝑚
𝑥→1
3 − √10 − 𝑥
𝑥2 − 1
= 𝑙𝑖𝑚
𝑥→1
3 − √10 − 1
12 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
3 − √10 − 𝑥
𝑥2 − 1
= 𝑙𝑖𝑚
𝑥→1
(3 − √10 − 𝑥)(3 + √10− 𝑥)
( 𝑥 + 1)(𝑥 − 1)(3+ √10 − 𝑥)
= 𝑙𝑖𝑚
𝑥→1
(3)2
− (√10 − 𝑥)
2
( 𝑥 + 1)(𝑥 − 1)(3+ √10 − 𝑥)
=
= 𝑙𝑖𝑚
𝑥→1
9 − 10 + 𝑥
( 𝑥 + 1)(𝑥 − 1)(3 + √10 − 𝑥)
= 𝑙𝑖𝑚
𝑥→1
(−1 + 𝑥)
( 𝑥 + 1)(𝑥 − 1)(3+ √10− 𝑥)
= 𝑙𝑖𝑚
𝑥→1
1
( 𝑥 + 1)(3+ √10− 𝑥)
=
= 𝑙𝑖𝑚
𝑥→1
1
(1 + 1)(3 + √10− 1)
=
1
12
∴ 𝒍𝒊𝒎
𝒙→𝟏
𝟑 − √ 𝟏𝟎 − 𝒙
𝒙 𝟐 − 𝟏
=
𝟏
𝟏𝟐
__________________________________________________________________________________________
44. 𝑙𝑖𝑚
𝑥→3
2 − √ 𝑥 + 1
𝑥2 − 9
= 𝑙𝑖𝑚
𝑥→3
2 − √3 + 1
32 − 9
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→3
2 − √ 𝑥 + 1
𝑥2 − 9
= 𝑙𝑖𝑚
𝑥→3
(2 − √ 𝑥 + 1)(2+ √ 𝑥 + 1)
( 𝑥 + 3)(𝑥 − 3)(2+ √ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→3
(2)2
− (√ 𝑥 + 1)
2
( 𝑥 + 3)(𝑥 − 3)(2 + √ 𝑥 + 1)
=
- 15.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 15
= 𝑙𝑖𝑚
𝑥→3
4 − 𝑥 − 1
( 𝑥 + 3)(𝑥 − 3)(2 + √ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→3
−(𝑥 − 3)
( 𝑥 + 3)(𝑥 − 3)(2+ √ 𝑥 + 1)
= 𝑙𝑖𝑚
𝑥→3
−1
( 𝑥 + 3)(2+ √ 𝑥 + 1)
=
= 𝑙𝑖𝑚
𝑥→3
−1
( 𝑥 + 3)(2 + √ 𝑥 + 1)
= −
1
24
∴ 𝒍𝒊𝒎
𝒙→𝟑
𝟐 − √ 𝒙 + 𝟏
𝒙 𝟐 − 𝟗
= −
𝟏
𝟐𝟒
__________________________________________________________________________________________
45. 𝑙𝑖𝑚
𝑥→1
√ 𝑥 + 3 − 2
𝑥2 − 3𝑥 + 2
= 𝑙𝑖𝑚
𝑥→1
√1 + 3 − 2
12 − 31 + 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√ 𝑥 + 3 − 2
𝑥2 − 3𝑥 + 2
= 𝑙𝑖𝑚
𝑥→1
(√ 𝑥 + 3 − 2)(√ 𝑥 + 3 + 2)
( 𝑥 − 1)(𝑥 − 2)(√ 𝑥 + 3 + 2)
= 𝑙𝑖𝑚
𝑥→1
(√ 𝑥 + 3)
2
− (2)2
( 𝑥 − 1)(𝑥 − 2)(√ 𝑥 + 3 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
𝑥 + 3 − 4
( 𝑥 − 1)(𝑥 − 2)(√ 𝑥 + 3 + 2)
= 𝑙𝑖𝑚
𝑥→1
(𝑥 − 1)
( 𝑥 − 1)(𝑥 − 2)(√ 𝑥 + 3 + 2)
= 𝑙𝑖𝑚
𝑥→1
1
(𝑥 − 2)(√ 𝑥 + 3 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
1
(1 − 2)(√1+ 3 + 2)
= −
1
4
∴ 𝒍𝒊𝒎
𝒙→𝟏
√ 𝒙 + 𝟑 − 𝟐
𝒙 𝟐 − 𝟑𝒙 + 𝟐
= −
𝟏
𝟒
__________________________________________________________________________________________
46. 𝑙𝑖𝑚
𝑥→2
𝑥2
− 4
√ 𝑥 + 2 − √3𝑥 − 2
= 𝑙𝑖𝑚
𝑥→2
22
− 4
√2 + 2 − √3 ∙ 2 − 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
𝑥2
− 4
√ 𝑥 + 2 − √3𝑥 − 2
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(𝑥 − 2)(√ 𝑥 + 2 + √3𝑥 − 2)
(√ 𝑥 + 2 − √3𝑥 − 2)(√ 𝑥 + 2 + √3𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(𝑥 − 2)(√ 𝑥 + 2 + √3𝑥 − 2)
(√ 𝑥 + 2)
2
− (√3𝑥 − 2)
2
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(𝑥 − 2)(√ 𝑥 + 2 + √3𝑥 − 2)
𝑥 + 2 − 3𝑥 + 2
=
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(𝑥 − 2)(√ 𝑥 + 2 + √3𝑥 − 2)
−2𝑥 + 4
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(𝑥 − 2)(√ 𝑥 + 2 + √3𝑥 − 2)
−2(𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 + 2)(√ 𝑥 + 2 + √3𝑥 − 2)
−2
= 𝑙𝑖𝑚
𝑥→2
−
(2 + 2)(√2+ 2 + √3 ∙ 2 − 2)
2
=
= 𝑙𝑖𝑚
𝑥→2
−
(2 + 2)(√2+ 2 + √3∙ 2 − 2)
2
= −
16
2
= −8 ∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 𝟐
− 𝟒
√ 𝒙 + 𝟐 − √ 𝟑𝒙 − 𝟐
= −𝟖
__________________________________________________________________________________________
47. 𝑙𝑖𝑚
𝑥→1
√𝑥2 − 3𝑥 + 3 − √𝑥2 + 3𝑥 − 3
𝑥2 − 3𝑥 + 2
= 𝑙𝑖𝑚
𝑥→1
√12 − 3 ∙ 1 + 3 − √12 + 3 ∙ 1 − 3
1 − 3 ∙ 1 + 2
=
0
0
- 16.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 16
(temos uma indeterminação)
𝑙𝑖𝑚
𝑥→1
√𝑥2 − 3𝑥 + 3 − √𝑥2 + 3𝑥 − 3
𝑥2 − 3𝑥 + 2
= 𝑙𝑖𝑚
𝑥→1
(√𝑥2 − 3𝑥 + 3 − √𝑥2 + 3𝑥 − 3)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
( 𝑥 − 1)(𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→1
(√𝑥2 − 3𝑥 + 3 − √𝑥2 + 3𝑥 − 3)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
( 𝑥 − 1)(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
(√𝑥2 − 3𝑥 + 3)
2
− (√ 𝑥2 + 3𝑥 − 3)
2
( 𝑥 − 1)(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
𝑥2
− 3𝑥 + 3 − 𝑥2
− 3𝑥 + 3
( 𝑥 − 1)(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
−3𝑥 + 3 − 3𝑥 + 3
( 𝑥 − 1)(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
−6𝑥 + 6
( 𝑥 − 1)(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
−6(𝑥 − 1)
( 𝑥 − 1)(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
−
6
(𝑥 − 2)(√𝑥2 − 3𝑥 + 3 + √𝑥2 + 3𝑥 − 3)
=
= 𝑙𝑖𝑚
𝑥→1
−
6
(1 − 2)(√12 − 3 ∙ 1 + 3 + √12 + 3 ∙ 1 − 3)
=
6
2
= 3
∴ 𝒍𝒊𝒎
𝒙→𝟏
√𝒙 𝟐 − 𝟑𝒙 + 𝟑 − √𝒙 𝟐 + 𝟑𝒙 − 𝟑
𝒙 𝟐 − 𝟑𝒙 + 𝟐
= 𝟑
48. 𝑙𝑖𝑚
𝑥→2
√3𝑥 − 2 − 2
√4𝑥 + 1 − 3
= 𝑙𝑖𝑚
𝑥→2
√3 ∙ 2 − 2 − 2
√4 ∙ 2 + 1 − 3
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√3𝑥 − 2 − 2
√4𝑥 + 1 − 3
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√4𝑥 + 1 + 3)
(√4𝑥 + 1 − 3)(√4𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√4𝑥 + 1 + 3)
(√4𝑥 + 1)
2
− (3)2
=
- 17.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 17
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√4𝑥 + 1 + 3)
(√4𝑥 + 1)
2
− (3)2
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√4𝑥 + 1 + 3)
(√4𝑥 + 1)
2
− (3)2
=
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√4𝑥 + 1 + 3)
4𝑥 + 1 − 9
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√4𝑥 + 1 + 3)
(4𝑥 − 8)
=
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥 − 2 − 2)(√3𝑥 − 2 + 2)(√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
[(√3𝑥 − 2)
2
− (2)2
](√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[(√3𝑥 − 2)
2
− (2)2
](√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
[3𝑥 − 2 − 4](√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(3𝑥 − 6)(√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
3(𝑥 − 2)(√4𝑥 + 1 + 3)
4(𝑥 − 2)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
3(√4𝑥 + 1 + 3)
4(√3𝑥 − 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
3 ∙ (√4 ∙ 2 + 1 + 3)
4 ∙ (√3 ∙ 2 − 2 + 2)
=
18
16
=
9
8
∴ 𝒍𝒊𝒎
𝒙→𝟐
√ 𝟑𝒙 − 𝟐 − 𝟐
√ 𝟒𝒙 + 𝟏 − 𝟑
=
𝟗
𝟖
Obs.: aqui o conjugado foi aplicado separadamente, no próximo limite aplicaremos de uma só vez. Veja!
__________________________________________________________________________________________
49. 𝑙𝑖𝑚
𝑥→4
√2𝑥 + 1 − 3
√ 𝑥 − 2 − √2
= 𝑙𝑖𝑚
𝑥→4
√24 + 1 − 3
√4 − 2 − √2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→4
√2𝑥 + 1 − 3
√ 𝑥 − 2 − √2
= 𝑙𝑖𝑚
𝑥→4
(√2𝑥 + 1 − 3)(√2𝑥 + 1 + 3)(√ 𝑥 − 2 + √2)
(√ 𝑥 − 2 − √2)(√ 𝑥 − 2 + √2)(√2𝑥 + 1 + 3)
=
= 𝑙𝑖𝑚
𝑥→4
[(√2𝑥 + 1)
2
− (3)2
](√ 𝑥 − 2 + √2)
[(√ 𝑥 − 2)
2
− (√2)
2
](√2𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→4
[2𝑥 + 1 − 9](√ 𝑥 − 2 + √2)
[ 𝑥 − 2 − 2](√2𝑥 + 1 + 3)
=
= 𝑙𝑖𝑚
𝑥→4
(2𝑥 − 8)(√ 𝑥 − 2 + √2)
(𝑥 − 4)(√2𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→4
2(𝑥 − 4)(√ 𝑥 − 2 + √2)
(𝑥 − 4)(√2𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→4
2 ∙ (√ 𝑥 − 2 + √2)
(√2𝑥 + 1 + 3)
=
= 𝑙𝑖𝑚
𝑥→4
2 ∙ (√ 𝑥 − 2 + √2)
(√2𝑥 + 1 + 3)
= = 𝑙𝑖𝑚
𝑥→4
2 ∙ (√4− 2 + √2)
(√2 ∙ 4 + 1 + 3)
=
4√2
6
=
2√2
3
∴ 𝒍𝒊𝒎
𝒙→𝟒
√ 𝟐𝒙 + 𝟏 − 𝟑
√ 𝒙 − 𝟐 − √ 𝟐
=
𝟐√ 𝟐
𝟑
__________________________________________________________________________________________
50. 𝑙𝑖𝑚
𝑥→6
4 − √10 + 𝑥
2 − √10 − 𝑥
= 𝑙𝑖𝑚
𝑥→6
4 − √10 + 6
2 − √10 − 6
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
- 18.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 18
𝑙𝑖𝑚
𝑥→6
4 − √10 + 𝑥
2 − √10 − 𝑥
= 𝑙𝑖𝑚
𝑥→6
(4 − √10 + 𝑥)(4 + √10+ 𝑥)(2 + √10 − 𝑥)
(2 − √10 − 𝑥)(2 + √10− 𝑥)(4 + √10 + 𝑥)
=
= 𝑙𝑖𝑚
𝑥→6
[(4)2
− (√10 + 𝑥)
2
](2 + √10− 𝑥)
[(2)2 − (√10 − 𝑥)
2
](4 + √10+ 𝑥)
= 𝑙𝑖𝑚
𝑥→6
[16 − 10 − 𝑥](2+ √10 − 𝑥)
[4 − 10 + 𝑥](4 + √10 + 𝑥)
=
= 𝑙𝑖𝑚
𝑥→6
(6 − 𝑥)(2 + √10 − 𝑥)
−(6 − 𝑥)(4 + √10 + 𝑥)
= 𝑙𝑖𝑚
𝑥→6
(6 − 𝑥)(2 + √10 − 𝑥)
−(6 − 𝑥)(4 + √10 + 𝑥)
= 𝑙𝑖𝑚 −
𝑥→6
(2 + √10 − 𝑥)
(4 + √10 + 𝑥)
=
= 𝑙𝑖𝑚 −
𝑥→6
(2 + √10 − 6)
(4 + √10 + 6)
= −
4
8
= −
1
2
∴ 𝒍𝒊𝒎
𝒙→𝟔
𝟒 − √ 𝟏𝟎 + 𝒙
𝟐 − √ 𝟏𝟎 − 𝒙
= −
𝟏
𝟐
__________________________________________________________________________________________
51. 𝑙𝑖𝑚
𝑥→0
√3𝑥 + 4 − √ 𝑥 + 4
√ 𝑥 + 1 − 1
= 𝑙𝑖𝑚
𝑥→0
√3 ∙ 0 + 4 − √0 + 4
√0 + 1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1)(√3𝑥 + 4 − √ 𝑥 + 4)(√3𝑥 + 4 + √ 𝑥 + 4)
(√ 𝑥 + 1 − 1)(√ 𝑥 + 1 + 1)(√3𝑥 + 4 + √ 𝑥 + 4)
=
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1) [(√3𝑥 + 4)
2
− (√ 𝑥 + 4)
2
]
[(√ 𝑥 + 1)
2
− (1)2](√3𝑥 + 4 − √ 𝑥 + 4)
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1)[3𝑥 + 4 − 𝑥 − 4]
[ 𝑥 + 1 − 1](√3𝑥 + 4 + √ 𝑥 + 4)
=
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1)[3𝑥 − 𝑥]
𝑥(√3𝑥 + 4 + √ 𝑥 + 4)
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1) ∙ 2𝑥
𝑥 ∙ (√3𝑥 + 4 + √ 𝑥 + 4)
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1) ∙ 2
(√3𝑥 + 4 + √ 𝑥 + 4)
=
= 𝑙𝑖𝑚
𝑥→0
(√0 + 1 + 1) ∙ 2
(√3∙ 0 + 4 + √0 + 4)
=
4
4
= 1 ∴ 𝒍𝒊𝒎
𝒙→𝟎
√ 𝟑𝒙 + 𝟒 − √ 𝒙 + 𝟒
√ 𝒙 + 𝟏 − 𝟏
= 𝟏
__________________________________________________________________________________________
52. 𝑙𝑖𝑚
𝑥→2
√𝑥2 + 𝑥 − 2 − √𝑥2 − 𝑥 + 2
√ 𝑥 + 2 − 2
= 𝑙𝑖𝑚
𝑥→2
√22 + 2 − 2 − √22 − 2 + 2
√2 + 2 − 2
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚. )
𝑙𝑖𝑚
𝑥→2
√𝑥2 + 𝑥 − 2 − √𝑥2 − 𝑥 + 2
√ 𝑥 + 2 − 2
=
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)(√𝑥2 + 𝑥 − 2 − √𝑥2 − 𝑥 + 2)(√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
(√ 𝑥 + 2 − 2)(√ 𝑥 + 2 + 2)(√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
- 19.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 19
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)[(√𝑥2 + 𝑥 − 2)
2
− (√𝑥2 − 𝑥 + 2)
2
]
[(√ 𝑥 + 2)
2
− (2)2](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)[ 𝑥2
+ 𝑥 − 2 − 𝑥2
+ 𝑥 − 2]
[ 𝑥 + 2 − 4](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)[2𝑥 − 4]
[ 𝑥 − 2](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)2[ 𝑥 − 2]
[ 𝑥 − 2](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2) ∙ 2
(√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(√2 + 2 + 2) ∙ 2
(√22 + 2 − 2 + √22 − 2 + 2)
=
8
4
= 2 ∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝒙 𝟐 + 𝒙 − 𝟐 − √𝒙 𝟐 − 𝒙 + 𝟐
√ 𝒙 + 𝟐 − 𝟐
= 𝟐
__________________________________________________________________________________________
53. 𝑙𝑖𝑚
𝑥→2
√2𝑥2 − 3𝑥 + 2 − 2
√3𝑥2 − 5𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
√2 ∙ 22 − 3 ∙ 2 + 2 − 2
√3 ∙ 22 − 5 ∙ 2 − 1 − 1
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√2𝑥2 − 3𝑥 + 2 − 2
√3𝑥2 − 5𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
(√2𝑥2 − 3𝑥 + 2 − 2)(√2𝑥2 − 3𝑥 + 2 + 2)(√3𝑥2 − 5𝑥 − 1 + 1)
(√3𝑥2 − 5𝑥 − 1 − 1)(√3𝑥2 − 5𝑥 − 1 + 1)(√2𝑥2 − 3𝑥 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[(√2𝑥2 − 3𝑥 + 2)
2
− (2)2
](√3𝑥2 − 5𝑥 − 1 + 1)
[(√3𝑥2 − 5𝑥 − 1)
2
− (1)2](√2𝑥2 − 3𝑥 + 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
[2𝑥2
− 3𝑥 + 2 − 4](√3𝑥2 − 5𝑥 − 1 + 1)
[3𝑥2 − 5𝑥 − 1 − 1](√2𝑥2 − 3𝑥 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[2𝑥2
− 3𝑥 − 2](√3𝑥2 − 5𝑥 − 1 + 1)
[3𝑥2 − 5𝑥 − 2](√2𝑥2 − 3𝑥 + 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 − 2)(2𝑥 + 1)(√3𝑥2 − 5𝑥 − 1 + 1)
( 𝑥 − 2)(3𝑥 + 1)(√2𝑥2 − 3𝑥 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[2 ∙ (2) + 1](√3 ∙ (2)2 − 5 ∙ (2)− 1 + 1)
[3 ∙ (2) + 1](√2 ∙ (2)2 − 3 ∙ (2)+ 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
5 ∙ (√12 − 10 − 1 + 1)
7 ∙ (√8 − 6 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
5 ∙ (1 + 1)
7 ∙ (2 + 2)
=
5 ∙ 2
7 ∙ 4
=
10
28
=
5
14
∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝟐𝒙 𝟐 − 𝟑𝒙 + 𝟐 − 𝟐
√𝟑𝒙 𝟐 − 𝟓𝒙 − 𝟏 − 𝟏
=
𝟓
𝟏𝟒
__________________________________________________________________________________________
54. 𝑙𝑖𝑚
𝑥→−1
√3𝑥2 + 4𝑥 + 2 − 1
√𝑥2 + 3𝑥 + 6 − 2
= 𝑙𝑖𝑚
𝑥→−1
√3 ∙ (−1)2 + 4 ∙ (−1) + 2 − 1
√(−1)2 + 3 ∙ (−1) + 6 − 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚. )
𝑙𝑖𝑚
𝑥→−1
√3𝑥2 + 4𝑥 + 2 − 1
√𝑥2 + 3𝑥 + 6 − 2
= 𝑙𝑖𝑚
𝑥→−1
(√3𝑥2 + 4𝑥 + 2 − 1)(√3𝑥2 + 4𝑥 + 2 + 1)((√𝑥2 + 3𝑥 + 6 + 2))
(√𝑥2 + 3𝑥 + 6 − 2)(√𝑥2 + 3𝑥 + 6 + 2)(√3𝑥2 + 4𝑥 + 2 + 1)
=
- 20.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 20
= 𝑙𝑖𝑚
𝑥→−1
[(√3𝑥2 + 4𝑥 + 2)
2
− (1)2
](√𝑥2 + 3𝑥 + 6 + 2)
[(√𝑥2 + 3𝑥 + 6)
2
− (2)2](√3𝑥2 + 4𝑥 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[3𝑥2
+ 4𝑥 + 2 − 1](√𝑥2 + 3𝑥 + 6 + 2)
[ 𝑥2 + 3𝑥 + 6 − 4](√3𝑥2 + 4𝑥 + 2 + 1)
= 𝑙𝑖𝑚
𝑥→−1
[3𝑥2
+ 4𝑥 + 1](√𝑥2 + 3𝑥 + 6 + 2)
[ 𝑥2 + 3𝑥 + 2](√3𝑥2 + 4𝑥 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1)(3𝑥 + 1)(√𝑥2 + 3𝑥 + 6 + 2)
( 𝑥 + 1)( 𝑥 + 2)(√3𝑥2 + 4𝑥 + 2 + 1)
= 𝑙𝑖𝑚
𝑥→−1
(3𝑥 + 1)(√𝑥2 + 3𝑥 + 6 + 2)
( 𝑥 + 2)(√3𝑥2 + 4𝑥 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[3(−1) + 1](√(−1)2 + 3(−1) + 6 + 2)
(−1 + 2)(√3(−1)2 + 4(−1)+ 2 + 1)
= 𝑙𝑖𝑚
𝑥→−1
[−3 + 1](√1 − 3 + 6 + 2)
1 ∙ (√3 − 4 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[−3 + 1](2+ 2)
1 ∙ (1 + 1)
=
−2 ∙ 4
2
= −4 ∴ 𝒍𝒊𝒎
𝒙→−𝟏
√𝟑𝒙 𝟐 + 𝟒𝒙 + 𝟐 − 𝟏
√𝒙 𝟐 + 𝟑𝒙 + 𝟔 − 𝟐
= −𝟒
__________________________________________________________________________________________
55. 𝑙𝑖𝑚
𝑥→2
𝑥 − 2
√3𝑥 − 5
3
− 1
= 𝑙𝑖𝑚
𝑥→2
2 − 2
√3∙ 2 − 5
3
− 1
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Atenção!! Você já sabe. x3 - y3 = (x - y)(x2 + xy + y2)
𝑙𝑖𝑚
𝑥→2
𝑥 − 2
√3𝑥 − 5
3
− 1
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2)
(√3𝑥 − 5
3
− 1)
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ 1 + 12
]
(√3𝑥 − 5
3
− 1) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ 1 + 12]
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ 1 + 12
]
(√3𝑥 − 5
3
− 1) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ ( √3𝑥 − 5
3
) + 1]
( √3𝑥 − 5
3
) ∙ (√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ (√3𝑥 − 5
3
) + (√3𝑥 − 5
3
) − (√3𝑥 − 5
3
)
2
− (√3𝑥 − 5
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
( √3𝑥 − 5
3
)
3
+ (√3𝑥 − 5
3
)
2
+ ( √3𝑥 − 5
3
) − (√3𝑥 − 5
3
)
2
− ( √3𝑥 − 5
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
( √3𝑥 − 5
3
)
3
+ (√3𝑥 − 5
3
) − (√3𝑥 − 5
3
) − 1
=
- 21.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 21
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
(3𝑥 − 5) + (√3𝑥 − 5
3
) − (√3𝑥 − 5
3
) − 1
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
(3𝑥 − 5) − 1
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
3𝑥 − 5 − 1
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
3𝑥 − 6
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
3(𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→2
[(√3 ∙ 2 − 5
3
)
2
+ (√3∙ 2 − 5
3
) + 1]
3
=
3
3
= 1 ∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 − 𝟐
√ 𝟑𝒙 − 𝟓
𝟑
− 𝟏
= 𝟏
_________________________________________________________________________________________
56. 𝑙𝑖𝑚
𝑥→0
√ 𝑥 + 1
3
− 1
𝑥
= 𝑙𝑖𝑚
𝑥→0
√0+ 1
3
− 1
0
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→0
√ 𝑥 + 1
3
− 1
𝑥
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1
3
− 1) ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) ∙ 1 + 12
]
𝑥 ∙ [( √ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) ∙ 1 + 12]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
− 1) ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
𝑥 ∙ [(√ 𝑥 + 13
)
2
+ (√ 𝑥 + 13
) ∙ 1 + 12]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
) ∙ (√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) ∙ (√ 𝑥 + 1
3
) + ( √ 𝑥 + 1
3
) ∙ 1 − (√ 𝑥 + 1
3
)
2
− (√ 𝑥 + 1
3
) − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
)
3
+ (√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) − (√ 𝑥 + 1
3
)
2
− (√ 𝑥 + 1
3
) − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
)
3
+ (√ 𝑥 + 1
3
) − (√ 𝑥 + 1
3
) − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ ( √ 𝑥 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
)
3
− 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
𝑥 + 1 − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→0
𝑥
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
1
[(√ 𝑥 + 1
3
)
2
+ ( √ 𝑥 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→0
1
[(√0 + 1
3
)
2
+ ( √0+ 1
3
) + 1]
=
1
3
∴ 𝒍𝒊𝒎
𝒙→𝟎
√ 𝒙 + 𝟏
𝟑
− 𝟏
𝒙
=
𝟏
𝟑
- 22.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 22
__________________________________________________________________________________________
57. 𝑙𝑖𝑚
𝑥→−1
𝑥 + 1
√2𝑥 + 3
3
− 1
= 𝑙𝑖𝑚
𝑥→−1
−1 + 1
√2(−1)+ 3
3
− 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→−1
𝑥 + 1
√2𝑥 + 3
3
− 1
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1)
(√2𝑥 + 3
3
− 1)
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
)(1) + (1)2
]
(√2𝑥 + 3
3
− 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
)(1) + (1)2]
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
( √2𝑥 + 3
3
− 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
( √2𝑥 + 33
)(√2𝑥 + 33
)
2
+ (√2𝑥 + 33
)( √2𝑥 + 33
) + (√2𝑥 + 33
) − 1(√2𝑥 + 33
)
2
− ( √2𝑥 + 33
) − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
( √2𝑥 + 3
3
)
3
+ (√2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
) − (√2𝑥 + 3
3
)
2
− (√2𝑥 + 3
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
(2𝑥 + 3) + ( √2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) − ( √2𝑥 + 3
3
)
2
− (√2𝑥 + 3
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
(2𝑥 + 3) − 1
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
2𝑥 + 3 − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 33
)
2
+ (√2𝑥 + 33
) + 1]
2𝑥 + 2
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 33
)
2
+ (√2𝑥 + 33
) + 1]
2( 𝑥 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
2
= 𝑙𝑖𝑚
𝑥→−1
[(√2 ∙ (−1) + 3
3
)
2
+ (√2∙ (−1)+ 3
3
) + 1]
2
=
= 𝑙𝑖𝑚
𝑥→−1
[(√−2+ 3
3
)
2
+ (√−2 + 3
3
) + 1]
2
= 𝑙𝑖𝑚
𝑥→−1
[(1)2
+ 1 + 1]
2
=
3
2
∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 + 𝟏
√ 𝟐𝒙+ 𝟑
𝟑
− 𝟏
=
𝟑
𝟐
__________________________________________________________________________________________
58. 𝑙𝑖𝑚
𝑥→0
√8 − 2𝑥 + 𝑥23
− 2
𝑥 − 𝑥2
= 𝑙𝑖𝑚
𝑥→0
√8− 2(0)+ (0)23
− 2
(0)− (0)2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
- 23.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 23
𝑙𝑖𝑚
𝑥→0
√8 − 2𝑥 + 𝑥23
− 2
𝑥 − 𝑥2
= 𝑙𝑖𝑚
𝑥→0
(√8 − 2𝑥 + 𝑥23
− 2)[(√8 − 2𝑥 + 𝑥23
)
2
+ ( √8− 2𝑥 + 𝑥23
)(2)+ (2)2
]
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ (√8 − 2𝑥 + 𝑥23
)(2) + (2)2]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
− 2) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
𝑥(1 − 𝑥) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
) ∙ ( √8− 2𝑥 + 𝑥23
)
2
+ ( √8− 2𝑥 + 𝑥23
) ∙ 2( √8− 2𝑥 + 𝑥23
) + 4( √8− 2𝑥 + 𝑥23
) − 2 ∙ ( √8− 2𝑥 + 𝑥23
)
2
− 4 ∙ ( √8− 2𝑥 + 𝑥23
) − 8
𝑥(1− 𝑥)[( √8− 2𝑥 + 𝑥23
)
2
+ 2( √8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
)
3
+ 2( √8− 2𝑥 + 𝑥23
)
2
+ 4( √8 − 2𝑥 + 𝑥23
) − 2 ∙ ( √8− 2𝑥 + 𝑥23
)
2
− 4 ∙ ( √8 − 2𝑥 + 𝑥23
) − 8
𝑥(1 − 𝑥) [( √8− 2𝑥 + 𝑥23
)
2
+ 2( √8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
)
3
+ 2( √8− 2𝑥 + 𝑥23
)
2
+ 4( √8 − 2𝑥 + 𝑥23
) − 2 ∙ ( √8− 2𝑥 + 𝑥23
)
2
− 4 ∙ ( √8 − 2𝑥 + 𝑥23
) − 8
𝑥(1 − 𝑥) [( √8− 2𝑥 + 𝑥23
)
2
+ 2( √8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
(√8 − 2𝑥 + 𝑥23
)
3
− 8
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
8 − 2𝑥 + 𝑥2
− 8
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
−2𝑥 + 𝑥2
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
𝑥(−2 + 𝑥)
𝑥(1 − 𝑥) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
(−2 + 𝑥)
(1 − 𝑥) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
(−2 + 0)
(1 − 0) [(√8− 2 ∙ 0 + 023
)
2
+ 2(√8 − 2 ∙ 0 + 023
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
−2
[(√8
3
)
2
+ 2(√8
3
) + 4]
=
−2
4 + 4 + 4
= −
2
12
= −
1
6
∴ 𝒍𝒊𝒎
𝒙→𝟎
√𝟖 − 𝟐𝒙 + 𝒙 𝟐𝟑
− 𝟐
𝒙 − 𝒙 𝟐
= −
𝟏
𝟔
__________________________________________________________________________________________
59. 𝑙𝑖𝑚
𝑥→0
1 − √1− 𝑥
3
1 + √3𝑥 − 1
3
= 𝑙𝑖𝑚
𝑥→0
1 − √1− 0
3
1 + √3 ∙ 0 − 1
3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
- 24.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 24
𝑙𝑖𝑚
𝑥→0
1 − √1 − 𝑥
3
1 + √3𝑥 − 1
3
= 𝑙𝑖𝑚
𝑥→0
(1 − √1− 𝑥
3
) ∙ [(1)2
+ (1)( √1 − 𝑥
3
) + ( √1 − 𝑥
3
)
2
] ∙ [(1)2
− (1)( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
]
(1 + √3𝑥 − 1
3
) ∙ [(1)2 − (1)( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
] ∙ [(1)2 + (1)( √1 − 𝑥
3
) + ( √1 − 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
(1 − √1 − 𝑥
3
) ∙ [1 + ( √1− 𝑥
3
) + (√1 − 𝑥
3
)
2
] ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
(1 + √3𝑥 − 1
3
) ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
] ∙ [1 + ( √1− 𝑥
3
) + (√1 − 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 + ( √1− 𝑥
3
) + ( √1− 𝑥
3
)
2
− ( √1− 𝑥
3
) − ( √1 − 𝑥
3
)
2
− ( √1 − 𝑥
3
)
3
] ∙ [1 − ( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
]
[1 − ( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
+ ( √3𝑥 − 1
3
) − ( √3𝑥 − 1
3
)
2
+ ( √3𝑥 − 1
3
)
3
] ∙ [1 + ( √1 − 𝑥
3
) + ( √1 − 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 − (√1− 𝑥
3
)
3
] ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
[1 + (√3𝑥 − 1
3
)
3
] ∙ [1 + (√1 − 𝑥
3
) + (√1− 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 − 1 + 𝑥] ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
[1 + 3𝑥 − 1] ∙ [1 + (√1 − 𝑥
3
) + (√1− 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
𝑥 ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
3𝑥 ∙ [1 + (√1 − 𝑥
3
) + ( √1− 𝑥
3
)
2
]
= 𝑙𝑖𝑚
𝑥→0
[1 − (√3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
]
3 ∙ [1 + (√1 − 𝑥
3
) + ( √1− 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 − (√3∙ 0 − 1
3
) + (√3 ∙ 0 − 1
3
)
2
]
3 ∙ [1 + (√1− 0
3
) + (√1 − 0
3
)
2
]
= 𝑙𝑖𝑚
𝑥→0
[1 − (√−1
3
) + ( √−1
3
)
2
]
3 ∙ [1 + (√1
3
) + (√1
3
)
2
]
=
𝑙𝑖𝑚
𝑥→0
[1 − (√−1
3
) + (√−1
3
)
2
]
3 ∙ [1 + (√13
) + (√13
)
2
]
=
1 + 1 + 1
3 ∙ (1 + 1 + 1)
=
3
9
=
1
3
∴ 𝒍𝒊𝒎
𝒙→𝟎
𝟏 − √ 𝟏 − 𝒙
𝟑
𝟏 + √ 𝟑𝒙 − 𝟏
𝟑
=
𝟏
𝟑
__________________________________________________________________________________________
60. 𝑙𝑖𝑚
𝑥→−2
√2− 3𝑥3
− 2
1 + √2𝑥 + 3
3
= 𝑙𝑖𝑚
𝑥→−2
√2 − 3 ∙ (−2)3
− 2
1 + √2 ∙ (−2) + 3
3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→−2
√2 − 3𝑥
3
− 2
1 + √2𝑥 + 3
3 =
= 𝑙𝑖𝑚
𝑥→−2
(√2 − 3𝑥3
− 2) ∙ [(√2 − 3𝑥3
)
2
+ (√2 − 3𝑥3
)(2) + (2)2] ∙ [(1)2 − (1)(√2𝑥 + 33
) + (√2𝑥 + 33
)
2
]
(1 + √2𝑥 + 33
) ∙ [(1)2 − (1)(√2𝑥 + 33
) + (√2𝑥 + 33
)
2
] ∙ [(√2 − 3𝑥3
)
2
+ (√2 − 3𝑥3
)(2) + (2)2]
=
= 𝑙𝑖𝑚
𝑥→−2
(√2 − 3𝑥
3
− 2) [(√2− 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4] ∙ [1 − (√2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
(1 + √2𝑥 + 3
3
) ∙ [1 − (√2𝑥 + 3
3
) + (√2𝑥 + 3
3
)
2
] ∙ [(√2− 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4]
=
- 25.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 25
= 𝑙𝑖𝑚
𝑥→−2
[( √2− 3𝑥
3
)
3
+ 2( √2 − 3𝑥
3
)
2
+ 4( √2− 3𝑥
3
) − 2( √2 − 3𝑥
3
)
2
− 4( √2− 3𝑥
3
) − 8] ∙ [1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
[1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
) − ( √2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
)
3
] ∙ [( √2− 3𝑥
3
)
2
+ 2( √2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
[(2 − 3𝑥) + 2( √2 − 3𝑥
3
)
2
+ 4( √2− 3𝑥
3
) − 2( √2 − 3𝑥
3
)
2
− 4( √2− 3𝑥
3
) − 8] ∙ [1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
[1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
) − ( √2𝑥 + 3
3
)
2
+ (2𝑥 + 3)] ∙ [( √2− 3𝑥
3
)
2
+ 2( √2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
[(2 − 3𝑥) − 8] ∙ [1 − ( √2𝑥 + 3
3
) + (√2𝑥 + 3
3
)
2
]
[1 + (2𝑥 + 3)] ∙ [(√2 − 3𝑥
3
)
2
+ 2(√2− 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
(2 − 3𝑥 − 8) ∙ [1 − (√2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
(1 + 2𝑥 + 3) ∙ [(√2− 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
(3𝑥 − 6) ∙ [1 − (√2𝑥 + 3
3
) + (√2𝑥 + 3
3
)
2
]
(2𝑥 + 4) ∙ [(√2 − 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ ( 𝑥 − 2) ∙ [1 − (√2(−2) + 3
3
) + (√2(−2)+ 3
3
)
2
]
−2 ∙ ( 𝑥 − 2) ∙ [(√2 − 3(−2)3
)
2
+ 2 (√2 − 3(−2)3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ [1 − (√−4+ 3
3
) + (√−4 + 3
3
)
2
]
−2 ∙ [(√2 + 6
3
)
2
+ 2(√2+ 6
3
) + 4]
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ [1 − (−1) + (−1)2]
−2 ∙ [(2)2 + 2(2) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ [1 + 1 + 1]
−2 ∙ [4 + 4 + 4]
= −
9
24
= −
3
8
∴ 𝒍𝒊𝒎
𝒙→−𝟐
√ 𝟐 − 𝟑𝒙
𝟑
− 𝟐
𝟏 + √ 𝟐𝒙+ 𝟑
𝟑
= −
𝟑
𝟖
__________________________________________________________________________________________
61. 𝑙𝑖𝑚
𝑥→2
√3𝑥2 − 7𝑥 + 1
3
+ 1
√2𝑥2 − 5𝑥 + 3
3
− 1
= 𝑙𝑖𝑚
𝑥→2
√3 ∙ (2)2 − 7 ∙ (2) + 1
3
+ 1
√2 ∙ (2)2 − 5 ∙ (2) + 3
3
− 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√3𝑥2 − 7𝑥 + 1
3
+ 1
√2𝑥2 − 5𝑥 + 3
3
− 1
=
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥2 − 7𝑥 + 1
3
+ 1)∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
)(1) + (1)2
] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
)(1) + (1)2
]
(√2𝑥2
− 5𝑥 + 3
3
− 1)∙ [(√2𝑥2
− 5𝑥 + 3
3
)
2
+ (√2𝑥2
− 5𝑥 + 3
3
)(1) + (1)2
] ∙ [(√3𝑥2
− 7𝑥 + 1
3
)
2
− (√3𝑥2
− 7𝑥 + 1
3
)(1) + (1)2
]
=
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥2 − 7𝑥 + 1
3
+ 1)∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
(√2𝑥2
− 5𝑥 + 3
3
− 1)∙ [(√2𝑥2
− 5𝑥 + 3
3
)
2
+ (√2𝑥2
− 5𝑥 + 3
3
) + 1] ∙ [(√3𝑥2
− 7𝑥 + 1
3
)
2
− (√3𝑥2
− 7𝑥 + 1
3
) + 1]
=
- 26.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 26
= 𝑙𝑖𝑚
𝑥→2
[( √3𝑥2 − 7𝑥 + 1
3
)
3
− (√3𝑥2 − 7𝑥 + 1
3
)
2
+ ( √3𝑥2 − 7𝑥 + 1
3
) + (√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
[( √2𝑥2 − 5𝑥 + 3
3
)
3
+ (√2𝑥2 − 5𝑥 + 3
3
)
2
+ ( √2𝑥2 − 5𝑥 + 3
3
) − (√2𝑥2 − 5𝑥 + 3
3
)
2
− (√2𝑥2 − 5𝑥 + 3
3
) − 1] ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
[(3𝑥2
− 7𝑥 + 1) − (√3𝑥2 − 7𝑥 + 1
3
)
2
+ ( √3𝑥2 − 7𝑥 + 1
3
) + (√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
[(2𝑥2 − 5𝑥 + 3) + (√2𝑥2 − 5𝑥 + 3
3
)
2
+ ( √2𝑥2 − 5𝑥 + 3
3
) − (√2𝑥2 − 5𝑥 + 3
3
)
2
− (√2𝑥2 − 5𝑥 + 3
3
) − 1] ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
[(3𝑥2
− 7𝑥 + 1) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
[(2𝑥2 − 5𝑥 + 3) − 1] ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(3𝑥2
− 7𝑥 + 2) ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ ( √2𝑥2 − 5𝑥 + 3
3
) + 1]
(2𝑥2 − 5𝑥 + 2) ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− ( √3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 − 2) ∙ (3𝑥 − 1) ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
( 𝑥 − 2) ∙ (2𝑥 − 1) ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(3𝑥 − 1) ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
(2𝑥 − 1) ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(3 ∙ 2 − 1) ∙ [(√2∙ 22 − 5 ∙ 2 + 3
3
)
2
+ (√2 ∙ 22 − 5 ∙ 2 + 3
3
) + 1]
(2 ∙ 2 − 1) ∙ [(√3∙ 22 − 7 ∙ 2 + 1
3
)
2
− (√3 ∙ 22 − 7 ∙ 2 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
5 ∙ [(√8− 10 + 3
3
)
2
+ (√8 − 10 + 3
3
) + 1]
3 ∙ [(√12− 14 + 1
3
)
2
− (√12− 14 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→2
5 ∙ [(1)2
+ 1 + 1]
3 ∙ [(−1)2 − (−1)+ 1]
=
= 𝑙𝑖𝑚
𝑥→2
5 ∙ [1 + 1 + 1]
3 ∙ [1 + 1 + 1]
=
15
9
=
5
3
∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝟑𝒙 𝟐 − 𝟕𝒙 + 𝟏
𝟑
+ 𝟏
√𝟐𝒙 𝟐 − 𝟓𝒙 + 𝟑
𝟑
− 𝟏
=
𝟓
𝟑
__________________________________________________________________________________________
62. 𝑙𝑖𝑚
𝑥→1
√5𝑥 + 4 − 3
√ 𝑥 − 2
3
+ 1
= 𝑙𝑖𝑚
𝑥→1
√5 ∙ 1 + 4 − 3
√1− 2
3
+ 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√5𝑥 + 4 − 3
√ 𝑥 − 2
3
+ 1
= 𝑙𝑖𝑚
𝑥→1
(√5𝑥 + 4 − 3)(√5𝑥 + 4 + 3) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
)(1)+ (1)2
]
(√ 𝑥 − 2
3
+ 1) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
)(1) + (1)2](√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(√5𝑥 + 4 − 3)(√5𝑥 + 4 + 3)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
(√ 𝑥 − 2
3
+ 1) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1](√5𝑥 + 4 + 3)
=
- 27.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 27
= 𝑙𝑖𝑚
𝑥→1
[(√5𝑥 + 4)
2
− (3)2
][(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
( √ 𝑥 − 2
3
+ 1)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1] (√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(5𝑥 + 4 − 9)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
[(√ 𝑥 − 2
3
)
3
−(√ 𝑥 − 2
3
)
2
+ ( √ 𝑥 − 2
3
) + (√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1](√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(5𝑥 − 5)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
[(√ 𝑥 − 2
3
)
3
− (√ 𝑥 − 2
3
)
2
+ (√ 𝑥 − 2
3
) + ( √ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1](√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(5𝑥 − 5)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
[ 𝑥 − 2 + 1](√5𝑥 + 4 + 3)
= 𝑙𝑖𝑚
𝑥→1
5( 𝑥 − 1) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
( 𝑥 − 1)(√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
(√5𝑥 + 4 + 3)
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [(√1− 2
3
)
2
− (√1 − 2
3
) + 1]
(√5 ∙ 1 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [(√−1
3
)
2
− (√−1
3
) + 1]
(3 + 3)
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [1 + 1 + 1]
(3 + 3)
=
15
6
=
5
2
∴ 𝒍𝒊𝒎
𝒙→𝟏
√ 𝟓𝒙+ 𝟒 − 𝟑
√ 𝒙− 𝟐
𝟑
+ 𝟏
=
𝟓
𝟐
__________________________________________________________________________________________
63. 𝑙𝑖𝑚
𝑥→2
√5𝑥 − 2
3
− 2
√ 𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
√5 ∙ 2 − 2
3
− 2
√2 − 1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√5𝑥 − 2
3
− 2
√ 𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
( √5𝑥 − 23
− 2) [(√5𝑥 − 23
)
2
+ (√5𝑥 − 23
)(2) + (2)2
](√ 𝑥 − 1 + 1)
(√ 𝑥 − 1 − 1)(√ 𝑥 − 1 + 1) [(√5𝑥 − 2
3
)
2
+ ( √5𝑥 − 2
3
)(2)+ (2)2]
=
= 𝑙𝑖𝑚
𝑥→2
( √5𝑥 − 2
3
− 2) ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4] (√ 𝑥 − 1 + 1)
(√ 𝑥 − 1 − 1)(√ 𝑥 − 1 + 1) ∙ [( √5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
[(√5𝑥 − 2
3
)
3
+ 2(√5𝑥 − 2
3
)
2
+ 4(√5𝑥 − 2
3
) − 2(√5𝑥 − 2
3
)
2
− 4(√5𝑥 − 2
3
) − 8](√ 𝑥 − 1 + 1)
[(√ 𝑥 − 1)
2
− (1)2] ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
[(5𝑥 − 2) + 2(√5𝑥 − 2
3
)
2
+ 4(√5𝑥 − 2
3
) − 2(√5𝑥 − 2
3
)
2
− 4(√5𝑥 − 2
3
) − 8](√ 𝑥 − 1 + 1)
[ 𝑥 − 1 − 1] ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
- 28.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 28
= 𝑙𝑖𝑚
𝑥→2
(5𝑥 − 10)(√ 𝑥 − 1 + 1)
( 𝑥 − 2) ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
= 𝑙𝑖𝑚
𝑥→2
5( 𝑥 − 2)(√ 𝑥 − 1 + 1)
( 𝑥 − 2) ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
5(√ 𝑥 − 1 + 1)
[(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
= 𝑙𝑖𝑚
𝑥→2
5(√2 − 1 + 1)
[(√5∙ 2 − 2
3
)
2
+ 2(√5 ∙ 2 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
5(1 + 1)
[(√10 − 2
3
)
2
+ 2(√10− 2
3
) + 4]
= = 𝑙𝑖𝑚
𝑥→2
10
[(√8
3
)
2
+ 2(√8
3
)+ 4]
=
= 𝑙𝑖𝑚
𝑥→2
10
[4 + 4 + 4]
=
10
12
=
5
6
∴ 𝒍𝒊𝒎
𝒙→𝟐
√ 𝟓𝒙 − 𝟐
𝟑
− 𝟐
√ 𝒙 − 𝟏 − 𝟏
=
𝟓
𝟔
__________________________________________________________________________________________
64. 𝑙𝑖𝑚
𝑥→1
√3𝑥3 − 5𝑥 + 6 − 2
√𝑥2 − 3𝑥 + 1
3
+ 1
= 𝑙𝑖𝑚
𝑥→2
√3 ∙ (1)3 − 5 ∙ (1) + 6 − 2
√(1)2 − 3 ∙ (1)+ 1
3
+ 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√3𝑥3 − 5𝑥 + 6 − 2
√𝑥2 − 3𝑥 + 1
3
+ 1
=
= 𝑙𝑖𝑚
𝑥→1
(√3𝑥3 − 5𝑥 + 6 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− ( √𝑥2 − 3𝑥 + 1
3
)(1) + (1)2
]
(√𝑥2 − 3𝑥 + 1
3
+ 1)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
)(1) + (1)2](√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(√3𝑥3 − 5𝑥 + 6 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− ( √𝑥2 − 3𝑥 + 1
3
) + 1]
(√𝑥2 − 3𝑥 + 1
3
+ 1)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1] (√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
[(√3𝑥3 − 5𝑥 + 6)
2
− (2)2
][(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
[(√𝑥2
− 3𝑥 + 1
3
)
3
− (√𝑥2
− 3𝑥 + 1
3
)
3
+ (√𝑥2
− 3𝑥 + 1
3
) + (√𝑥2
− 3𝑥 + 1
3
)
2
− (√𝑥2
− 3𝑥 + 1
3
) + 1](√3𝑥3
− 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
[(3𝑥3
− 5𝑥 + 6) − 4] [(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
[(√𝑥2 − 3𝑥 + 1
3
)
3
+ 1](√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(3𝑥3
− 5𝑥 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
[ 𝑥2 − 3𝑥 + 1 + 1](√3𝑥3 − 5𝑥 + 6 + 2)
=
- 29.
Limite - ExercíciosResolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 29
= 𝑙𝑖𝑚
𝑥→1
(3𝑥3
− 5𝑥 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
( 𝑥2 − 3𝑥 + 2)(√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)(3𝑥2
+ 3𝑥 − 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
( 𝑥 − 1)( 𝑥 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(3𝑥2
+ 3𝑥 − 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
( 𝑥 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(3 ∙ 12
+ 3 ∙ 1 − 2)[(√12 − 3 ∙ 1 + 1
3
)
2
− (√12 − 3 ∙ 1 + 1
3
) + 1]
(1 − 2)(√3∙ 13 − 5 ∙ 1 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
4 ∙ [1 + 1 + 1]
−1 ∙ (2 + 2)
= −
12
4
= −3 ∴ 𝒍𝒊𝒎
𝒙→𝟏
√𝟑𝒙 𝟑 − 𝟓𝒙 + 𝟔 − 𝟐
√𝒙 𝟐 − 𝟑𝒙 + 𝟏
𝟑
+ 𝟏
= −𝟑
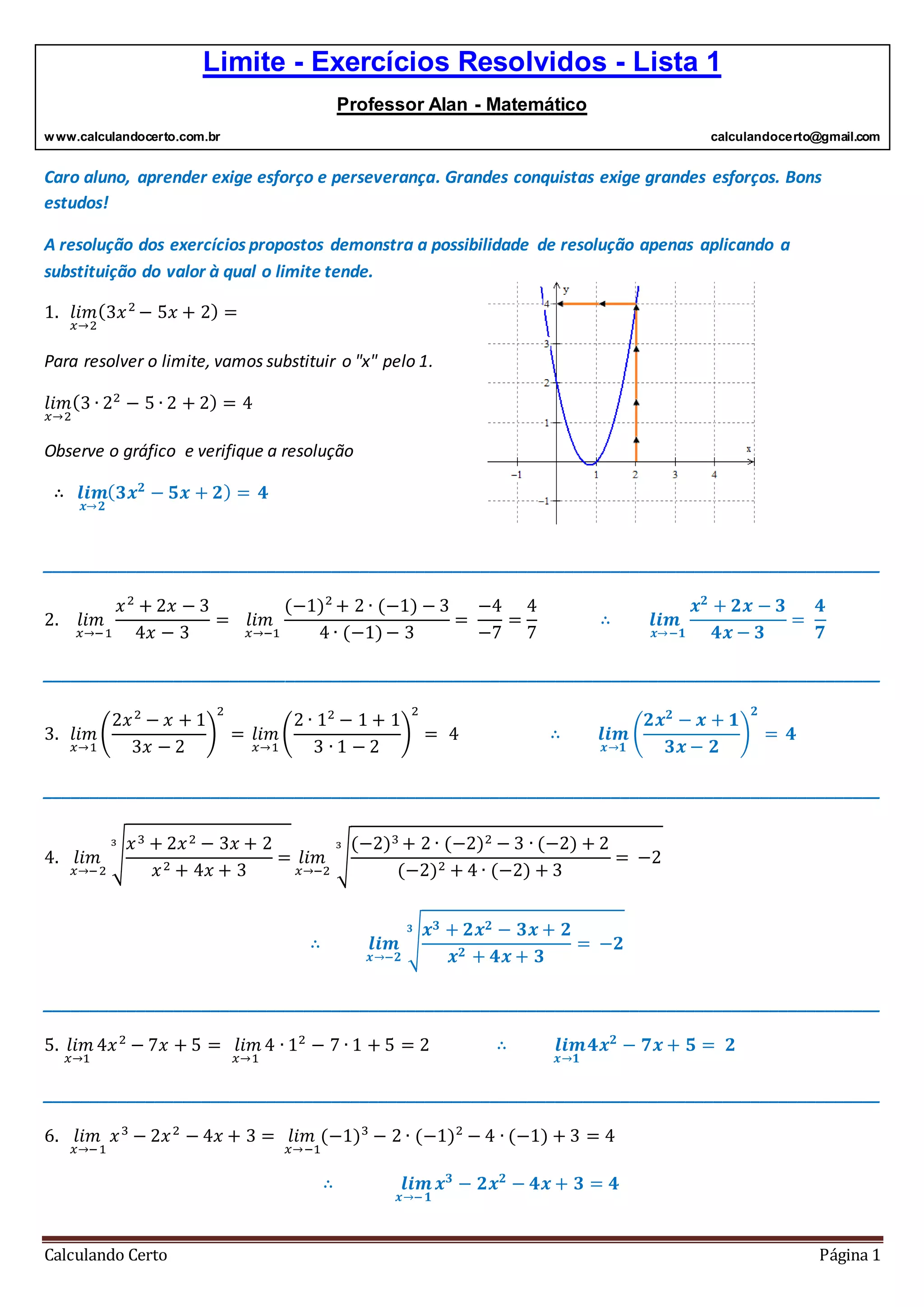
















(4𝑥 − 8)(√3𝑥 − 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[(√3𝑥 − 2)
2
− (2)2
](√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
[3𝑥 − 2 − 4](√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(3𝑥 − 6)(√4𝑥 + 1 + 3)
(4𝑥 − 8)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
3(𝑥 − 2)(√4𝑥 + 1 + 3)
4(𝑥 − 2)(√3𝑥 − 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
3(√4𝑥 + 1 + 3)
4(√3𝑥 − 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
3 ∙ (√4 ∙ 2 + 1 + 3)
4 ∙ (√3 ∙ 2 − 2 + 2)
=
18
16
=
9
8
∴ 𝒍𝒊𝒎
𝒙→𝟐
√ 𝟑𝒙 − 𝟐 − 𝟐
√ 𝟒𝒙 + 𝟏 − 𝟑
=
𝟗
𝟖
Obs.: aqui o conjugado foi aplicado separadamente, no próximo limite aplicaremos de uma só vez. Veja!
__________________________________________________________________________________________
49. 𝑙𝑖𝑚
𝑥→4
√2𝑥 + 1 − 3
√ 𝑥 − 2 − √2
= 𝑙𝑖𝑚
𝑥→4
√24 + 1 − 3
√4 − 2 − √2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→4
√2𝑥 + 1 − 3
√ 𝑥 − 2 − √2
= 𝑙𝑖𝑚
𝑥→4
(√2𝑥 + 1 − 3)(√2𝑥 + 1 + 3)(√ 𝑥 − 2 + √2)
(√ 𝑥 − 2 − √2)(√ 𝑥 − 2 + √2)(√2𝑥 + 1 + 3)
=
= 𝑙𝑖𝑚
𝑥→4
[(√2𝑥 + 1)
2
− (3)2
](√ 𝑥 − 2 + √2)
[(√ 𝑥 − 2)
2
− (√2)
2
](√2𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→4
[2𝑥 + 1 − 9](√ 𝑥 − 2 + √2)
[ 𝑥 − 2 − 2](√2𝑥 + 1 + 3)
=
= 𝑙𝑖𝑚
𝑥→4
(2𝑥 − 8)(√ 𝑥 − 2 + √2)
(𝑥 − 4)(√2𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→4
2(𝑥 − 4)(√ 𝑥 − 2 + √2)
(𝑥 − 4)(√2𝑥 + 1 + 3)
= 𝑙𝑖𝑚
𝑥→4
2 ∙ (√ 𝑥 − 2 + √2)
(√2𝑥 + 1 + 3)
=
= 𝑙𝑖𝑚
𝑥→4
2 ∙ (√ 𝑥 − 2 + √2)
(√2𝑥 + 1 + 3)
= = 𝑙𝑖𝑚
𝑥→4
2 ∙ (√4− 2 + √2)
(√2 ∙ 4 + 1 + 3)
=
4√2
6
=
2√2
3
∴ 𝒍𝒊𝒎
𝒙→𝟒
√ 𝟐𝒙 + 𝟏 − 𝟑
√ 𝒙 − 𝟐 − √ 𝟐
=
𝟐√ 𝟐
𝟑
__________________________________________________________________________________________
50. 𝑙𝑖𝑚
𝑥→6
4 − √10 + 𝑥
2 − √10 − 𝑥
= 𝑙𝑖𝑚
𝑥→6
4 − √10 + 6
2 − √10 − 6
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-17-320.jpg)

[(2)2 − (√10 − 𝑥)
2
](4 + √10+ 𝑥)
= 𝑙𝑖𝑚
𝑥→6
[16 − 10 − 𝑥](2+ √10 − 𝑥)
[4 − 10 + 𝑥](4 + √10 + 𝑥)
=
= 𝑙𝑖𝑚
𝑥→6
(6 − 𝑥)(2 + √10 − 𝑥)
−(6 − 𝑥)(4 + √10 + 𝑥)
= 𝑙𝑖𝑚
𝑥→6
(6 − 𝑥)(2 + √10 − 𝑥)
−(6 − 𝑥)(4 + √10 + 𝑥)
= 𝑙𝑖𝑚 −
𝑥→6
(2 + √10 − 𝑥)
(4 + √10 + 𝑥)
=
= 𝑙𝑖𝑚 −
𝑥→6
(2 + √10 − 6)
(4 + √10 + 6)
= −
4
8
= −
1
2
∴ 𝒍𝒊𝒎
𝒙→𝟔
𝟒 − √ 𝟏𝟎 + 𝒙
𝟐 − √ 𝟏𝟎 − 𝒙
= −
𝟏
𝟐
__________________________________________________________________________________________
51. 𝑙𝑖𝑚
𝑥→0
√3𝑥 + 4 − √ 𝑥 + 4
√ 𝑥 + 1 − 1
= 𝑙𝑖𝑚
𝑥→0
√3 ∙ 0 + 4 − √0 + 4
√0 + 1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1)(√3𝑥 + 4 − √ 𝑥 + 4)(√3𝑥 + 4 + √ 𝑥 + 4)
(√ 𝑥 + 1 − 1)(√ 𝑥 + 1 + 1)(√3𝑥 + 4 + √ 𝑥 + 4)
=
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1) [(√3𝑥 + 4)
2
− (√ 𝑥 + 4)
2
]
[(√ 𝑥 + 1)
2
− (1)2](√3𝑥 + 4 − √ 𝑥 + 4)
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1)[3𝑥 + 4 − 𝑥 − 4]
[ 𝑥 + 1 − 1](√3𝑥 + 4 + √ 𝑥 + 4)
=
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1)[3𝑥 − 𝑥]
𝑥(√3𝑥 + 4 + √ 𝑥 + 4)
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1) ∙ 2𝑥
𝑥 ∙ (√3𝑥 + 4 + √ 𝑥 + 4)
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1 + 1) ∙ 2
(√3𝑥 + 4 + √ 𝑥 + 4)
=
= 𝑙𝑖𝑚
𝑥→0
(√0 + 1 + 1) ∙ 2
(√3∙ 0 + 4 + √0 + 4)
=
4
4
= 1 ∴ 𝒍𝒊𝒎
𝒙→𝟎
√ 𝟑𝒙 + 𝟒 − √ 𝒙 + 𝟒
√ 𝒙 + 𝟏 − 𝟏
= 𝟏
__________________________________________________________________________________________
52. 𝑙𝑖𝑚
𝑥→2
√𝑥2 + 𝑥 − 2 − √𝑥2 − 𝑥 + 2
√ 𝑥 + 2 − 2
= 𝑙𝑖𝑚
𝑥→2
√22 + 2 − 2 − √22 − 2 + 2
√2 + 2 − 2
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚. )
𝑙𝑖𝑚
𝑥→2
√𝑥2 + 𝑥 − 2 − √𝑥2 − 𝑥 + 2
√ 𝑥 + 2 − 2
=
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)(√𝑥2 + 𝑥 − 2 − √𝑥2 − 𝑥 + 2)(√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
(√ 𝑥 + 2 − 2)(√ 𝑥 + 2 + 2)(√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-18-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 19
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)[(√𝑥2 + 𝑥 − 2)
2
− (√𝑥2 − 𝑥 + 2)
2
]
[(√ 𝑥 + 2)
2
− (2)2](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)[ 𝑥2
+ 𝑥 − 2 − 𝑥2
+ 𝑥 − 2]
[ 𝑥 + 2 − 4](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)[2𝑥 − 4]
[ 𝑥 − 2](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2)2[ 𝑥 − 2]
[ 𝑥 − 2](√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
= 𝑙𝑖𝑚
𝑥→2
(√ 𝑥 + 2 + 2) ∙ 2
(√𝑥2 + 𝑥 − 2 + √𝑥2 − 𝑥 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
(√2 + 2 + 2) ∙ 2
(√22 + 2 − 2 + √22 − 2 + 2)
=
8
4
= 2 ∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝒙 𝟐 + 𝒙 − 𝟐 − √𝒙 𝟐 − 𝒙 + 𝟐
√ 𝒙 + 𝟐 − 𝟐
= 𝟐
__________________________________________________________________________________________
53. 𝑙𝑖𝑚
𝑥→2
√2𝑥2 − 3𝑥 + 2 − 2
√3𝑥2 − 5𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
√2 ∙ 22 − 3 ∙ 2 + 2 − 2
√3 ∙ 22 − 5 ∙ 2 − 1 − 1
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√2𝑥2 − 3𝑥 + 2 − 2
√3𝑥2 − 5𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
(√2𝑥2 − 3𝑥 + 2 − 2)(√2𝑥2 − 3𝑥 + 2 + 2)(√3𝑥2 − 5𝑥 − 1 + 1)
(√3𝑥2 − 5𝑥 − 1 − 1)(√3𝑥2 − 5𝑥 − 1 + 1)(√2𝑥2 − 3𝑥 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[(√2𝑥2 − 3𝑥 + 2)
2
− (2)2
](√3𝑥2 − 5𝑥 − 1 + 1)
[(√3𝑥2 − 5𝑥 − 1)
2
− (1)2](√2𝑥2 − 3𝑥 + 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
[2𝑥2
− 3𝑥 + 2 − 4](√3𝑥2 − 5𝑥 − 1 + 1)
[3𝑥2 − 5𝑥 − 1 − 1](√2𝑥2 − 3𝑥 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[2𝑥2
− 3𝑥 − 2](√3𝑥2 − 5𝑥 − 1 + 1)
[3𝑥2 − 5𝑥 − 2](√2𝑥2 − 3𝑥 + 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 − 2)(2𝑥 + 1)(√3𝑥2 − 5𝑥 − 1 + 1)
( 𝑥 − 2)(3𝑥 + 1)(√2𝑥2 − 3𝑥 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
[2 ∙ (2) + 1](√3 ∙ (2)2 − 5 ∙ (2)− 1 + 1)
[3 ∙ (2) + 1](√2 ∙ (2)2 − 3 ∙ (2)+ 2 + 2)
= 𝑙𝑖𝑚
𝑥→2
5 ∙ (√12 − 10 − 1 + 1)
7 ∙ (√8 − 6 + 2 + 2)
=
= 𝑙𝑖𝑚
𝑥→2
5 ∙ (1 + 1)
7 ∙ (2 + 2)
=
5 ∙ 2
7 ∙ 4
=
10
28
=
5
14
∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝟐𝒙 𝟐 − 𝟑𝒙 + 𝟐 − 𝟐
√𝟑𝒙 𝟐 − 𝟓𝒙 − 𝟏 − 𝟏
=
𝟓
𝟏𝟒
__________________________________________________________________________________________
54. 𝑙𝑖𝑚
𝑥→−1
√3𝑥2 + 4𝑥 + 2 − 1
√𝑥2 + 3𝑥 + 6 − 2
= 𝑙𝑖𝑚
𝑥→−1
√3 ∙ (−1)2 + 4 ∙ (−1) + 2 − 1
√(−1)2 + 3 ∙ (−1) + 6 − 2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚. )
𝑙𝑖𝑚
𝑥→−1
√3𝑥2 + 4𝑥 + 2 − 1
√𝑥2 + 3𝑥 + 6 − 2
= 𝑙𝑖𝑚
𝑥→−1
(√3𝑥2 + 4𝑥 + 2 − 1)(√3𝑥2 + 4𝑥 + 2 + 1)((√𝑥2 + 3𝑥 + 6 + 2))
(√𝑥2 + 3𝑥 + 6 − 2)(√𝑥2 + 3𝑥 + 6 + 2)(√3𝑥2 + 4𝑥 + 2 + 1)
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-19-320.jpg)

[(√𝑥2 + 3𝑥 + 6)
2
− (2)2](√3𝑥2 + 4𝑥 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[3𝑥2
+ 4𝑥 + 2 − 1](√𝑥2 + 3𝑥 + 6 + 2)
[ 𝑥2 + 3𝑥 + 6 − 4](√3𝑥2 + 4𝑥 + 2 + 1)
= 𝑙𝑖𝑚
𝑥→−1
[3𝑥2
+ 4𝑥 + 1](√𝑥2 + 3𝑥 + 6 + 2)
[ 𝑥2 + 3𝑥 + 2](√3𝑥2 + 4𝑥 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1)(3𝑥 + 1)(√𝑥2 + 3𝑥 + 6 + 2)
( 𝑥 + 1)( 𝑥 + 2)(√3𝑥2 + 4𝑥 + 2 + 1)
= 𝑙𝑖𝑚
𝑥→−1
(3𝑥 + 1)(√𝑥2 + 3𝑥 + 6 + 2)
( 𝑥 + 2)(√3𝑥2 + 4𝑥 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[3(−1) + 1](√(−1)2 + 3(−1) + 6 + 2)
(−1 + 2)(√3(−1)2 + 4(−1)+ 2 + 1)
= 𝑙𝑖𝑚
𝑥→−1
[−3 + 1](√1 − 3 + 6 + 2)
1 ∙ (√3 − 4 + 2 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[−3 + 1](2+ 2)
1 ∙ (1 + 1)
=
−2 ∙ 4
2
= −4 ∴ 𝒍𝒊𝒎
𝒙→−𝟏
√𝟑𝒙 𝟐 + 𝟒𝒙 + 𝟐 − 𝟏
√𝒙 𝟐 + 𝟑𝒙 + 𝟔 − 𝟐
= −𝟒
__________________________________________________________________________________________
55. 𝑙𝑖𝑚
𝑥→2
𝑥 − 2
√3𝑥 − 5
3
− 1
= 𝑙𝑖𝑚
𝑥→2
2 − 2
√3∙ 2 − 5
3
− 1
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
Atenção!! Você já sabe. x3 - y3 = (x - y)(x2 + xy + y2)
𝑙𝑖𝑚
𝑥→2
𝑥 − 2
√3𝑥 − 5
3
− 1
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2)
(√3𝑥 − 5
3
− 1)
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ 1 + 12
]
(√3𝑥 − 5
3
− 1) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ 1 + 12]
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ 1 + 12
]
(√3𝑥 − 5
3
− 1) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ ( √3𝑥 − 5
3
) + 1]
( √3𝑥 − 5
3
) ∙ (√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) ∙ (√3𝑥 − 5
3
) + (√3𝑥 − 5
3
) − (√3𝑥 − 5
3
)
2
− (√3𝑥 − 5
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
( √3𝑥 − 5
3
)
3
+ (√3𝑥 − 5
3
)
2
+ ( √3𝑥 − 5
3
) − (√3𝑥 − 5
3
)
2
− ( √3𝑥 − 5
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
( √3𝑥 − 5
3
)
3
+ (√3𝑥 − 5
3
) − (√3𝑥 − 5
3
) − 1
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-20-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 21
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
(3𝑥 − 5) + (√3𝑥 − 5
3
) − (√3𝑥 − 5
3
) − 1
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
(3𝑥 − 5) − 1
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
3𝑥 − 5 − 1
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
3𝑥 − 6
=
= 𝑙𝑖𝑚
𝑥→2
(𝑥 − 2) ∙ [(√3𝑥 − 5
3
)
2
+ (√3𝑥 − 5
3
) + 1]
3(𝑥 − 2)
=
= 𝑙𝑖𝑚
𝑥→2
[(√3 ∙ 2 − 5
3
)
2
+ (√3∙ 2 − 5
3
) + 1]
3
=
3
3
= 1 ∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 − 𝟐
√ 𝟑𝒙 − 𝟓
𝟑
− 𝟏
= 𝟏
_________________________________________________________________________________________
56. 𝑙𝑖𝑚
𝑥→0
√ 𝑥 + 1
3
− 1
𝑥
= 𝑙𝑖𝑚
𝑥→0
√0+ 1
3
− 1
0
=
0
0
( 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→0
√ 𝑥 + 1
3
− 1
𝑥
= 𝑙𝑖𝑚
𝑥→0
(√ 𝑥 + 1
3
− 1) ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) ∙ 1 + 12
]
𝑥 ∙ [( √ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) ∙ 1 + 12]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
− 1) ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
𝑥 ∙ [(√ 𝑥 + 13
)
2
+ (√ 𝑥 + 13
) ∙ 1 + 12]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
) ∙ (√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) ∙ (√ 𝑥 + 1
3
) + ( √ 𝑥 + 1
3
) ∙ 1 − (√ 𝑥 + 1
3
)
2
− (√ 𝑥 + 1
3
) − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
)
3
+ (√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) − (√ 𝑥 + 1
3
)
2
− (√ 𝑥 + 1
3
) − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
)
3
+ (√ 𝑥 + 1
3
) − (√ 𝑥 + 1
3
) − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ ( √ 𝑥 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→0
( √ 𝑥 + 1
3
)
3
− 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
𝑥 + 1 − 1
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→0
𝑥
𝑥 ∙ [(√ 𝑥 + 1
3
)
2
+ (√ 𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→0
1
[(√ 𝑥 + 1
3
)
2
+ ( √ 𝑥 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→0
1
[(√0 + 1
3
)
2
+ ( √0+ 1
3
) + 1]
=
1
3
∴ 𝒍𝒊𝒎
𝒙→𝟎
√ 𝒙 + 𝟏
𝟑
− 𝟏
𝒙
=
𝟏
𝟑](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-21-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 22
__________________________________________________________________________________________
57. 𝑙𝑖𝑚
𝑥→−1
𝑥 + 1
√2𝑥 + 3
3
− 1
= 𝑙𝑖𝑚
𝑥→−1
−1 + 1
√2(−1)+ 3
3
− 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→−1
𝑥 + 1
√2𝑥 + 3
3
− 1
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1)
(√2𝑥 + 3
3
− 1)
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
)(1) + (1)2
]
(√2𝑥 + 3
3
− 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
)(1) + (1)2]
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
( √2𝑥 + 3
3
− 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
( √2𝑥 + 33
)(√2𝑥 + 33
)
2
+ (√2𝑥 + 33
)( √2𝑥 + 33
) + (√2𝑥 + 33
) − 1(√2𝑥 + 33
)
2
− ( √2𝑥 + 33
) − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
( √2𝑥 + 3
3
)
3
+ (√2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
) − (√2𝑥 + 3
3
)
2
− (√2𝑥 + 3
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
(2𝑥 + 3) + ( √2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) − ( √2𝑥 + 3
3
)
2
− (√2𝑥 + 3
3
) − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
(2𝑥 + 3) − 1
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
2𝑥 + 3 − 1
=
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 33
)
2
+ (√2𝑥 + 33
) + 1]
2𝑥 + 2
= 𝑙𝑖𝑚
𝑥→−1
( 𝑥 + 1) ∙ [(√2𝑥 + 33
)
2
+ (√2𝑥 + 33
) + 1]
2( 𝑥 + 1)
=
= 𝑙𝑖𝑚
𝑥→−1
[(√2𝑥 + 3
3
)
2
+ (√2𝑥 + 3
3
) + 1]
2
= 𝑙𝑖𝑚
𝑥→−1
[(√2 ∙ (−1) + 3
3
)
2
+ (√2∙ (−1)+ 3
3
) + 1]
2
=
= 𝑙𝑖𝑚
𝑥→−1
[(√−2+ 3
3
)
2
+ (√−2 + 3
3
) + 1]
2
= 𝑙𝑖𝑚
𝑥→−1
[(1)2
+ 1 + 1]
2
=
3
2
∴ 𝒍𝒊𝒎
𝒙→−𝟏
𝒙 + 𝟏
√ 𝟐𝒙+ 𝟑
𝟑
− 𝟏
=
𝟑
𝟐
__________________________________________________________________________________________
58. 𝑙𝑖𝑚
𝑥→0
√8 − 2𝑥 + 𝑥23
− 2
𝑥 − 𝑥2
= 𝑙𝑖𝑚
𝑥→0
√8− 2(0)+ (0)23
− 2
(0)− (0)2
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-22-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 23
𝑙𝑖𝑚
𝑥→0
√8 − 2𝑥 + 𝑥23
− 2
𝑥 − 𝑥2
= 𝑙𝑖𝑚
𝑥→0
(√8 − 2𝑥 + 𝑥23
− 2)[(√8 − 2𝑥 + 𝑥23
)
2
+ ( √8− 2𝑥 + 𝑥23
)(2)+ (2)2
]
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ (√8 − 2𝑥 + 𝑥23
)(2) + (2)2]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
− 2) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
𝑥(1 − 𝑥) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
) ∙ ( √8− 2𝑥 + 𝑥23
)
2
+ ( √8− 2𝑥 + 𝑥23
) ∙ 2( √8− 2𝑥 + 𝑥23
) + 4( √8− 2𝑥 + 𝑥23
) − 2 ∙ ( √8− 2𝑥 + 𝑥23
)
2
− 4 ∙ ( √8− 2𝑥 + 𝑥23
) − 8
𝑥(1− 𝑥)[( √8− 2𝑥 + 𝑥23
)
2
+ 2( √8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
)
3
+ 2( √8− 2𝑥 + 𝑥23
)
2
+ 4( √8 − 2𝑥 + 𝑥23
) − 2 ∙ ( √8− 2𝑥 + 𝑥23
)
2
− 4 ∙ ( √8 − 2𝑥 + 𝑥23
) − 8
𝑥(1 − 𝑥) [( √8− 2𝑥 + 𝑥23
)
2
+ 2( √8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
( √8− 2𝑥 + 𝑥23
)
3
+ 2( √8− 2𝑥 + 𝑥23
)
2
+ 4( √8 − 2𝑥 + 𝑥23
) − 2 ∙ ( √8− 2𝑥 + 𝑥23
)
2
− 4 ∙ ( √8 − 2𝑥 + 𝑥23
) − 8
𝑥(1 − 𝑥) [( √8− 2𝑥 + 𝑥23
)
2
+ 2( √8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
(√8 − 2𝑥 + 𝑥23
)
3
− 8
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
8 − 2𝑥 + 𝑥2
− 8
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
−2𝑥 + 𝑥2
𝑥(1 − 𝑥)[(√8 − 2𝑥 + 𝑥23
)
2
+ 2(√8 − 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
𝑥(−2 + 𝑥)
𝑥(1 − 𝑥) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
(−2 + 𝑥)
(1 − 𝑥) [(√8− 2𝑥 + 𝑥23
)
2
+ 2(√8− 2𝑥 + 𝑥23
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
(−2 + 0)
(1 − 0) [(√8− 2 ∙ 0 + 023
)
2
+ 2(√8 − 2 ∙ 0 + 023
) + 4]
=
= 𝑙𝑖𝑚
𝑥→0
−2
[(√8
3
)
2
+ 2(√8
3
) + 4]
=
−2
4 + 4 + 4
= −
2
12
= −
1
6
∴ 𝒍𝒊𝒎
𝒙→𝟎
√𝟖 − 𝟐𝒙 + 𝒙 𝟐𝟑
− 𝟐
𝒙 − 𝒙 𝟐
= −
𝟏
𝟔
__________________________________________________________________________________________
59. 𝑙𝑖𝑚
𝑥→0
1 − √1− 𝑥
3
1 + √3𝑥 − 1
3
= 𝑙𝑖𝑚
𝑥→0
1 − √1− 0
3
1 + √3 ∙ 0 − 1
3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-23-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 24
𝑙𝑖𝑚
𝑥→0
1 − √1 − 𝑥
3
1 + √3𝑥 − 1
3
= 𝑙𝑖𝑚
𝑥→0
(1 − √1− 𝑥
3
) ∙ [(1)2
+ (1)( √1 − 𝑥
3
) + ( √1 − 𝑥
3
)
2
] ∙ [(1)2
− (1)( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
]
(1 + √3𝑥 − 1
3
) ∙ [(1)2 − (1)( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
] ∙ [(1)2 + (1)( √1 − 𝑥
3
) + ( √1 − 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
(1 − √1 − 𝑥
3
) ∙ [1 + ( √1− 𝑥
3
) + (√1 − 𝑥
3
)
2
] ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
(1 + √3𝑥 − 1
3
) ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
] ∙ [1 + ( √1− 𝑥
3
) + (√1 − 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 + ( √1− 𝑥
3
) + ( √1− 𝑥
3
)
2
− ( √1− 𝑥
3
) − ( √1 − 𝑥
3
)
2
− ( √1 − 𝑥
3
)
3
] ∙ [1 − ( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
]
[1 − ( √3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
+ ( √3𝑥 − 1
3
) − ( √3𝑥 − 1
3
)
2
+ ( √3𝑥 − 1
3
)
3
] ∙ [1 + ( √1 − 𝑥
3
) + ( √1 − 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 − (√1− 𝑥
3
)
3
] ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
[1 + (√3𝑥 − 1
3
)
3
] ∙ [1 + (√1 − 𝑥
3
) + (√1− 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 − 1 + 𝑥] ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
[1 + 3𝑥 − 1] ∙ [1 + (√1 − 𝑥
3
) + (√1− 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
𝑥 ∙ [1 − (√3𝑥 − 1
3
) + (√3𝑥 − 1
3
)
2
]
3𝑥 ∙ [1 + (√1 − 𝑥
3
) + ( √1− 𝑥
3
)
2
]
= 𝑙𝑖𝑚
𝑥→0
[1 − (√3𝑥 − 1
3
) + ( √3𝑥 − 1
3
)
2
]
3 ∙ [1 + (√1 − 𝑥
3
) + ( √1− 𝑥
3
)
2
]
=
= 𝑙𝑖𝑚
𝑥→0
[1 − (√3∙ 0 − 1
3
) + (√3 ∙ 0 − 1
3
)
2
]
3 ∙ [1 + (√1− 0
3
) + (√1 − 0
3
)
2
]
= 𝑙𝑖𝑚
𝑥→0
[1 − (√−1
3
) + ( √−1
3
)
2
]
3 ∙ [1 + (√1
3
) + (√1
3
)
2
]
=
𝑙𝑖𝑚
𝑥→0
[1 − (√−1
3
) + (√−1
3
)
2
]
3 ∙ [1 + (√13
) + (√13
)
2
]
=
1 + 1 + 1
3 ∙ (1 + 1 + 1)
=
3
9
=
1
3
∴ 𝒍𝒊𝒎
𝒙→𝟎
𝟏 − √ 𝟏 − 𝒙
𝟑
𝟏 + √ 𝟑𝒙 − 𝟏
𝟑
=
𝟏
𝟑
__________________________________________________________________________________________
60. 𝑙𝑖𝑚
𝑥→−2
√2− 3𝑥3
− 2
1 + √2𝑥 + 3
3
= 𝑙𝑖𝑚
𝑥→−2
√2 − 3 ∙ (−2)3
− 2
1 + √2 ∙ (−2) + 3
3
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→−2
√2 − 3𝑥
3
− 2
1 + √2𝑥 + 3
3 =
= 𝑙𝑖𝑚
𝑥→−2
(√2 − 3𝑥3
− 2) ∙ [(√2 − 3𝑥3
)
2
+ (√2 − 3𝑥3
)(2) + (2)2] ∙ [(1)2 − (1)(√2𝑥 + 33
) + (√2𝑥 + 33
)
2
]
(1 + √2𝑥 + 33
) ∙ [(1)2 − (1)(√2𝑥 + 33
) + (√2𝑥 + 33
)
2
] ∙ [(√2 − 3𝑥3
)
2
+ (√2 − 3𝑥3
)(2) + (2)2]
=
= 𝑙𝑖𝑚
𝑥→−2
(√2 − 3𝑥
3
− 2) [(√2− 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4] ∙ [1 − (√2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
(1 + √2𝑥 + 3
3
) ∙ [1 − (√2𝑥 + 3
3
) + (√2𝑥 + 3
3
)
2
] ∙ [(√2− 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4]
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-24-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 25
= 𝑙𝑖𝑚
𝑥→−2
[( √2− 3𝑥
3
)
3
+ 2( √2 − 3𝑥
3
)
2
+ 4( √2− 3𝑥
3
) − 2( √2 − 3𝑥
3
)
2
− 4( √2− 3𝑥
3
) − 8] ∙ [1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
[1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
) − ( √2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
)
3
] ∙ [( √2− 3𝑥
3
)
2
+ 2( √2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
[(2 − 3𝑥) + 2( √2 − 3𝑥
3
)
2
+ 4( √2− 3𝑥
3
) − 2( √2 − 3𝑥
3
)
2
− 4( √2− 3𝑥
3
) − 8] ∙ [1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
[1 − ( √2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
+ ( √2𝑥 + 3
3
) − ( √2𝑥 + 3
3
)
2
+ (2𝑥 + 3)] ∙ [( √2− 3𝑥
3
)
2
+ 2( √2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
[(2 − 3𝑥) − 8] ∙ [1 − ( √2𝑥 + 3
3
) + (√2𝑥 + 3
3
)
2
]
[1 + (2𝑥 + 3)] ∙ [(√2 − 3𝑥
3
)
2
+ 2(√2− 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
(2 − 3𝑥 − 8) ∙ [1 − (√2𝑥 + 3
3
) + ( √2𝑥 + 3
3
)
2
]
(1 + 2𝑥 + 3) ∙ [(√2− 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
(3𝑥 − 6) ∙ [1 − (√2𝑥 + 3
3
) + (√2𝑥 + 3
3
)
2
]
(2𝑥 + 4) ∙ [(√2 − 3𝑥
3
)
2
+ 2(√2 − 3𝑥
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ ( 𝑥 − 2) ∙ [1 − (√2(−2) + 3
3
) + (√2(−2)+ 3
3
)
2
]
−2 ∙ ( 𝑥 − 2) ∙ [(√2 − 3(−2)3
)
2
+ 2 (√2 − 3(−2)3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ [1 − (√−4+ 3
3
) + (√−4 + 3
3
)
2
]
−2 ∙ [(√2 + 6
3
)
2
+ 2(√2+ 6
3
) + 4]
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ [1 − (−1) + (−1)2]
−2 ∙ [(2)2 + 2(2) + 4]
=
= 𝑙𝑖𝑚
𝑥→−2
3 ∙ [1 + 1 + 1]
−2 ∙ [4 + 4 + 4]
= −
9
24
= −
3
8
∴ 𝒍𝒊𝒎
𝒙→−𝟐
√ 𝟐 − 𝟑𝒙
𝟑
− 𝟐
𝟏 + √ 𝟐𝒙+ 𝟑
𝟑
= −
𝟑
𝟖
__________________________________________________________________________________________
61. 𝑙𝑖𝑚
𝑥→2
√3𝑥2 − 7𝑥 + 1
3
+ 1
√2𝑥2 − 5𝑥 + 3
3
− 1
= 𝑙𝑖𝑚
𝑥→2
√3 ∙ (2)2 − 7 ∙ (2) + 1
3
+ 1
√2 ∙ (2)2 − 5 ∙ (2) + 3
3
− 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√3𝑥2 − 7𝑥 + 1
3
+ 1
√2𝑥2 − 5𝑥 + 3
3
− 1
=
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥2 − 7𝑥 + 1
3
+ 1)∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
)(1) + (1)2
] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
)(1) + (1)2
]
(√2𝑥2
− 5𝑥 + 3
3
− 1)∙ [(√2𝑥2
− 5𝑥 + 3
3
)
2
+ (√2𝑥2
− 5𝑥 + 3
3
)(1) + (1)2
] ∙ [(√3𝑥2
− 7𝑥 + 1
3
)
2
− (√3𝑥2
− 7𝑥 + 1
3
)(1) + (1)2
]
=
= 𝑙𝑖𝑚
𝑥→2
(√3𝑥2 − 7𝑥 + 1
3
+ 1)∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
(√2𝑥2
− 5𝑥 + 3
3
− 1)∙ [(√2𝑥2
− 5𝑥 + 3
3
)
2
+ (√2𝑥2
− 5𝑥 + 3
3
) + 1] ∙ [(√3𝑥2
− 7𝑥 + 1
3
)
2
− (√3𝑥2
− 7𝑥 + 1
3
) + 1]
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-25-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 26
= 𝑙𝑖𝑚
𝑥→2
[( √3𝑥2 − 7𝑥 + 1
3
)
3
− (√3𝑥2 − 7𝑥 + 1
3
)
2
+ ( √3𝑥2 − 7𝑥 + 1
3
) + (√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
[( √2𝑥2 − 5𝑥 + 3
3
)
3
+ (√2𝑥2 − 5𝑥 + 3
3
)
2
+ ( √2𝑥2 − 5𝑥 + 3
3
) − (√2𝑥2 − 5𝑥 + 3
3
)
2
− (√2𝑥2 − 5𝑥 + 3
3
) − 1] ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
[(3𝑥2
− 7𝑥 + 1) − (√3𝑥2 − 7𝑥 + 1
3
)
2
+ ( √3𝑥2 − 7𝑥 + 1
3
) + (√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
[(2𝑥2 − 5𝑥 + 3) + (√2𝑥2 − 5𝑥 + 3
3
)
2
+ ( √2𝑥2 − 5𝑥 + 3
3
) − (√2𝑥2 − 5𝑥 + 3
3
)
2
− (√2𝑥2 − 5𝑥 + 3
3
) − 1] ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
[(3𝑥2
− 7𝑥 + 1) + 1] ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
[(2𝑥2 − 5𝑥 + 3) − 1] ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(3𝑥2
− 7𝑥 + 2) ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ ( √2𝑥2 − 5𝑥 + 3
3
) + 1]
(2𝑥2 − 5𝑥 + 2) ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− ( √3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
( 𝑥 − 2) ∙ (3𝑥 − 1) ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
( 𝑥 − 2) ∙ (2𝑥 − 1) ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(3𝑥 − 1) ∙ [(√2𝑥2 − 5𝑥 + 3
3
)
2
+ (√2𝑥2 − 5𝑥 + 3
3
) + 1]
(2𝑥 − 1) ∙ [(√3𝑥2 − 7𝑥 + 1
3
)
2
− (√3𝑥2 − 7𝑥 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
(3 ∙ 2 − 1) ∙ [(√2∙ 22 − 5 ∙ 2 + 3
3
)
2
+ (√2 ∙ 22 − 5 ∙ 2 + 3
3
) + 1]
(2 ∙ 2 − 1) ∙ [(√3∙ 22 − 7 ∙ 2 + 1
3
)
2
− (√3 ∙ 22 − 7 ∙ 2 + 1
3
) + 1]
=
= 𝑙𝑖𝑚
𝑥→2
5 ∙ [(√8− 10 + 3
3
)
2
+ (√8 − 10 + 3
3
) + 1]
3 ∙ [(√12− 14 + 1
3
)
2
− (√12− 14 + 1
3
) + 1]
= 𝑙𝑖𝑚
𝑥→2
5 ∙ [(1)2
+ 1 + 1]
3 ∙ [(−1)2 − (−1)+ 1]
=
= 𝑙𝑖𝑚
𝑥→2
5 ∙ [1 + 1 + 1]
3 ∙ [1 + 1 + 1]
=
15
9
=
5
3
∴ 𝒍𝒊𝒎
𝒙→𝟐
√𝟑𝒙 𝟐 − 𝟕𝒙 + 𝟏
𝟑
+ 𝟏
√𝟐𝒙 𝟐 − 𝟓𝒙 + 𝟑
𝟑
− 𝟏
=
𝟓
𝟑
__________________________________________________________________________________________
62. 𝑙𝑖𝑚
𝑥→1
√5𝑥 + 4 − 3
√ 𝑥 − 2
3
+ 1
= 𝑙𝑖𝑚
𝑥→1
√5 ∙ 1 + 4 − 3
√1− 2
3
+ 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√5𝑥 + 4 − 3
√ 𝑥 − 2
3
+ 1
= 𝑙𝑖𝑚
𝑥→1
(√5𝑥 + 4 − 3)(√5𝑥 + 4 + 3) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
)(1)+ (1)2
]
(√ 𝑥 − 2
3
+ 1) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
)(1) + (1)2](√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(√5𝑥 + 4 − 3)(√5𝑥 + 4 + 3)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
(√ 𝑥 − 2
3
+ 1) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1](√5𝑥 + 4 + 3)
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-26-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 27
= 𝑙𝑖𝑚
𝑥→1
[(√5𝑥 + 4)
2
− (3)2
][(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
( √ 𝑥 − 2
3
+ 1)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1] (√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(5𝑥 + 4 − 9)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
[(√ 𝑥 − 2
3
)
3
−(√ 𝑥 − 2
3
)
2
+ ( √ 𝑥 − 2
3
) + (√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1](√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(5𝑥 − 5)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
[(√ 𝑥 − 2
3
)
3
− (√ 𝑥 − 2
3
)
2
+ (√ 𝑥 − 2
3
) + ( √ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1](√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
(5𝑥 − 5)[(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
[ 𝑥 − 2 + 1](√5𝑥 + 4 + 3)
= 𝑙𝑖𝑚
𝑥→1
5( 𝑥 − 1) [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
( 𝑥 − 1)(√5𝑥 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [(√ 𝑥 − 2
3
)
2
− (√ 𝑥 − 2
3
) + 1]
(√5𝑥 + 4 + 3)
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [(√1− 2
3
)
2
− (√1 − 2
3
) + 1]
(√5 ∙ 1 + 4 + 3)
=
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [(√−1
3
)
2
− (√−1
3
) + 1]
(3 + 3)
= 𝑙𝑖𝑚
𝑥→1
5 ∙ [1 + 1 + 1]
(3 + 3)
=
15
6
=
5
2
∴ 𝒍𝒊𝒎
𝒙→𝟏
√ 𝟓𝒙+ 𝟒 − 𝟑
√ 𝒙− 𝟐
𝟑
+ 𝟏
=
𝟓
𝟐
__________________________________________________________________________________________
63. 𝑙𝑖𝑚
𝑥→2
√5𝑥 − 2
3
− 2
√ 𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
√5 ∙ 2 − 2
3
− 2
√2 − 1 − 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→2
√5𝑥 − 2
3
− 2
√ 𝑥 − 1 − 1
= 𝑙𝑖𝑚
𝑥→2
( √5𝑥 − 23
− 2) [(√5𝑥 − 23
)
2
+ (√5𝑥 − 23
)(2) + (2)2
](√ 𝑥 − 1 + 1)
(√ 𝑥 − 1 − 1)(√ 𝑥 − 1 + 1) [(√5𝑥 − 2
3
)
2
+ ( √5𝑥 − 2
3
)(2)+ (2)2]
=
= 𝑙𝑖𝑚
𝑥→2
( √5𝑥 − 2
3
− 2) ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4] (√ 𝑥 − 1 + 1)
(√ 𝑥 − 1 − 1)(√ 𝑥 − 1 + 1) ∙ [( √5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
[(√5𝑥 − 2
3
)
3
+ 2(√5𝑥 − 2
3
)
2
+ 4(√5𝑥 − 2
3
) − 2(√5𝑥 − 2
3
)
2
− 4(√5𝑥 − 2
3
) − 8](√ 𝑥 − 1 + 1)
[(√ 𝑥 − 1)
2
− (1)2] ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
[(5𝑥 − 2) + 2(√5𝑥 − 2
3
)
2
+ 4(√5𝑥 − 2
3
) − 2(√5𝑥 − 2
3
)
2
− 4(√5𝑥 − 2
3
) − 8](√ 𝑥 − 1 + 1)
[ 𝑥 − 1 − 1] ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-27-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 28
= 𝑙𝑖𝑚
𝑥→2
(5𝑥 − 10)(√ 𝑥 − 1 + 1)
( 𝑥 − 2) ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
= 𝑙𝑖𝑚
𝑥→2
5( 𝑥 − 2)(√ 𝑥 − 1 + 1)
( 𝑥 − 2) ∙ [(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
5(√ 𝑥 − 1 + 1)
[(√5𝑥 − 2
3
)
2
+ 2(√5𝑥 − 2
3
) + 4]
= 𝑙𝑖𝑚
𝑥→2
5(√2 − 1 + 1)
[(√5∙ 2 − 2
3
)
2
+ 2(√5 ∙ 2 − 2
3
) + 4]
=
= 𝑙𝑖𝑚
𝑥→2
5(1 + 1)
[(√10 − 2
3
)
2
+ 2(√10− 2
3
) + 4]
= = 𝑙𝑖𝑚
𝑥→2
10
[(√8
3
)
2
+ 2(√8
3
)+ 4]
=
= 𝑙𝑖𝑚
𝑥→2
10
[4 + 4 + 4]
=
10
12
=
5
6
∴ 𝒍𝒊𝒎
𝒙→𝟐
√ 𝟓𝒙 − 𝟐
𝟑
− 𝟐
√ 𝒙 − 𝟏 − 𝟏
=
𝟓
𝟔
__________________________________________________________________________________________
64. 𝑙𝑖𝑚
𝑥→1
√3𝑥3 − 5𝑥 + 6 − 2
√𝑥2 − 3𝑥 + 1
3
+ 1
= 𝑙𝑖𝑚
𝑥→2
√3 ∙ (1)3 − 5 ∙ (1) + 6 − 2
√(1)2 − 3 ∙ (1)+ 1
3
+ 1
=
0
0
(𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎çã𝑜)
𝑙𝑖𝑚
𝑥→1
√3𝑥3 − 5𝑥 + 6 − 2
√𝑥2 − 3𝑥 + 1
3
+ 1
=
= 𝑙𝑖𝑚
𝑥→1
(√3𝑥3 − 5𝑥 + 6 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− ( √𝑥2 − 3𝑥 + 1
3
)(1) + (1)2
]
(√𝑥2 − 3𝑥 + 1
3
+ 1)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
)(1) + (1)2](√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(√3𝑥3 − 5𝑥 + 6 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− ( √𝑥2 − 3𝑥 + 1
3
) + 1]
(√𝑥2 − 3𝑥 + 1
3
+ 1)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1] (√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
[(√3𝑥3 − 5𝑥 + 6)
2
− (2)2
][(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
[(√𝑥2
− 3𝑥 + 1
3
)
3
− (√𝑥2
− 3𝑥 + 1
3
)
3
+ (√𝑥2
− 3𝑥 + 1
3
) + (√𝑥2
− 3𝑥 + 1
3
)
2
− (√𝑥2
− 3𝑥 + 1
3
) + 1](√3𝑥3
− 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
[(3𝑥3
− 5𝑥 + 6) − 4] [(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
[(√𝑥2 − 3𝑥 + 1
3
)
3
+ 1](√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(3𝑥3
− 5𝑥 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
[ 𝑥2 − 3𝑥 + 1 + 1](√3𝑥3 − 5𝑥 + 6 + 2)
=](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-28-320.jpg)
![Limite - Exercícios Resolvidos - Lista 1
Professor Alan - Matemático
www.calculandocerto.com.br calculandocerto@gmail.com
Calculando Certo Página 29
= 𝑙𝑖𝑚
𝑥→1
(3𝑥3
− 5𝑥 + 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
( 𝑥2 − 3𝑥 + 2)(√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
( 𝑥 − 1)(3𝑥2
+ 3𝑥 − 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
( 𝑥 − 1)( 𝑥 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(3𝑥2
+ 3𝑥 − 2)[(√𝑥2 − 3𝑥 + 1
3
)
2
− (√𝑥2 − 3𝑥 + 1
3
) + 1]
( 𝑥 − 2)(√3𝑥3 − 5𝑥 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
(3 ∙ 12
+ 3 ∙ 1 − 2)[(√12 − 3 ∙ 1 + 1
3
)
2
− (√12 − 3 ∙ 1 + 1
3
) + 1]
(1 − 2)(√3∙ 13 − 5 ∙ 1 + 6 + 2)
=
= 𝑙𝑖𝑚
𝑥→1
4 ∙ [1 + 1 + 1]
−1 ∙ (2 + 2)
= −
12
4
= −3 ∴ 𝒍𝒊𝒎
𝒙→𝟏
√𝟑𝒙 𝟑 − 𝟓𝒙 + 𝟔 − 𝟐
√𝒙 𝟐 − 𝟑𝒙 + 𝟏
𝟑
+ 𝟏
= −𝟑](https://image.slidesharecdn.com/limite-lista1-150614013659-lva1-app6891/85/Limite-lista-1-29-320.jpg)