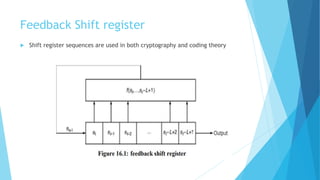
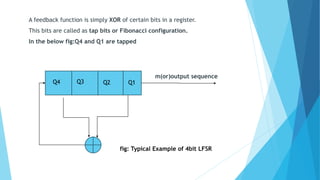
This document summarizes a presentation about linear feedback shift registers (LFSRs). It defines an LFSR as a type of feedback shift register that uses a linear feedback function, typically an XOR of certain bits in the register. An LFSR can generate long pseudo-random sequences of 1s and 0s before repeating, with the period of an n-bit LFSR being 2n - 1. The feedback function is applied after each shift to determine the next bit. LFSRs are commonly used in cryptography due to their ability to generate random-looking sequences. The document provides an example of a 4-bit LFSR and discusses the use of primitive polynomials to ensure maximum periods. It also lists some applications of LFSRs

1. MAHARAJA INSTITUTE OF TECHNOLOGY THANDAVAPURA
(An ISO 9001:2015 and ISO 21001:2018 Certified Institution)
(Affiliated to VTU, Belagavi and approved by AICTE, New Delhi)
NH 766,Nanjangud Taluk ,Mysuru -571302
18EC744 – CRYPTOGRAPHY
TOPIC : “Linear Feedback Shift Registers {LFSR}”
Present by,
Name : PRANAV D K & SINDHUSHREE N
USN : 4MN20EC018 & 4MN20EC025
Semester :7th

2. Feedback Shift register
 Shift register sequences are used in both cryptography and coding theory

3.  A feedback shift register is made up of two parts: a shift register and a
feedback function.
 The shift register is a sequence of bits. (The length of a shift register is
figured in bits; if it is n bits long, it is called an n-bit shift register.) Each
time a bit is needed; all of the bits in the shift register are shifted 1 bit to the
right.

4. Linear feedback shift registers:
 The simplest kind of feedback shift registers is Linear feedback shift registers.
 LFSRs are the most common type of shift registers used in cryptography.
 LFSR’S is device that can create long seemingly random sequence, of one’s and
zero’s.
 2n - 1-bit-long pseudo random sequence can be generated before repeating.
 n : number of bits (4,8,16,32)bits
 32 bits is the maximum

5. A feedback function is simply XOR of certain bits in a register.
This bits are called as tap bits or Fibonacci configuration.
In the below fig:Q4 and Q1 are tapped
Q4 Q3 Q2 Q1
fig: Typical Example of 4bit LFSR
m(or)output sequence

6.  For a particular LFSR to be a maximum period LFSR a feedback polynomial is formed
form tap sequence and constant 1 must be primitive polynomial of mod2
i.e,when we divided XT + 1 from below equation we should get remainder as 0
(T=2n -1)
X1 X2 X3 X4
Feedback function
f(x)=1+X1+X2+X3+X4

7. APPLICATIONS:
 Computer simulation of random process
 Error correcting codes
 This design used in FPGA’s

9. Reference: Applied Cryptography 2nd edition
Author(S):Bruce Schneier