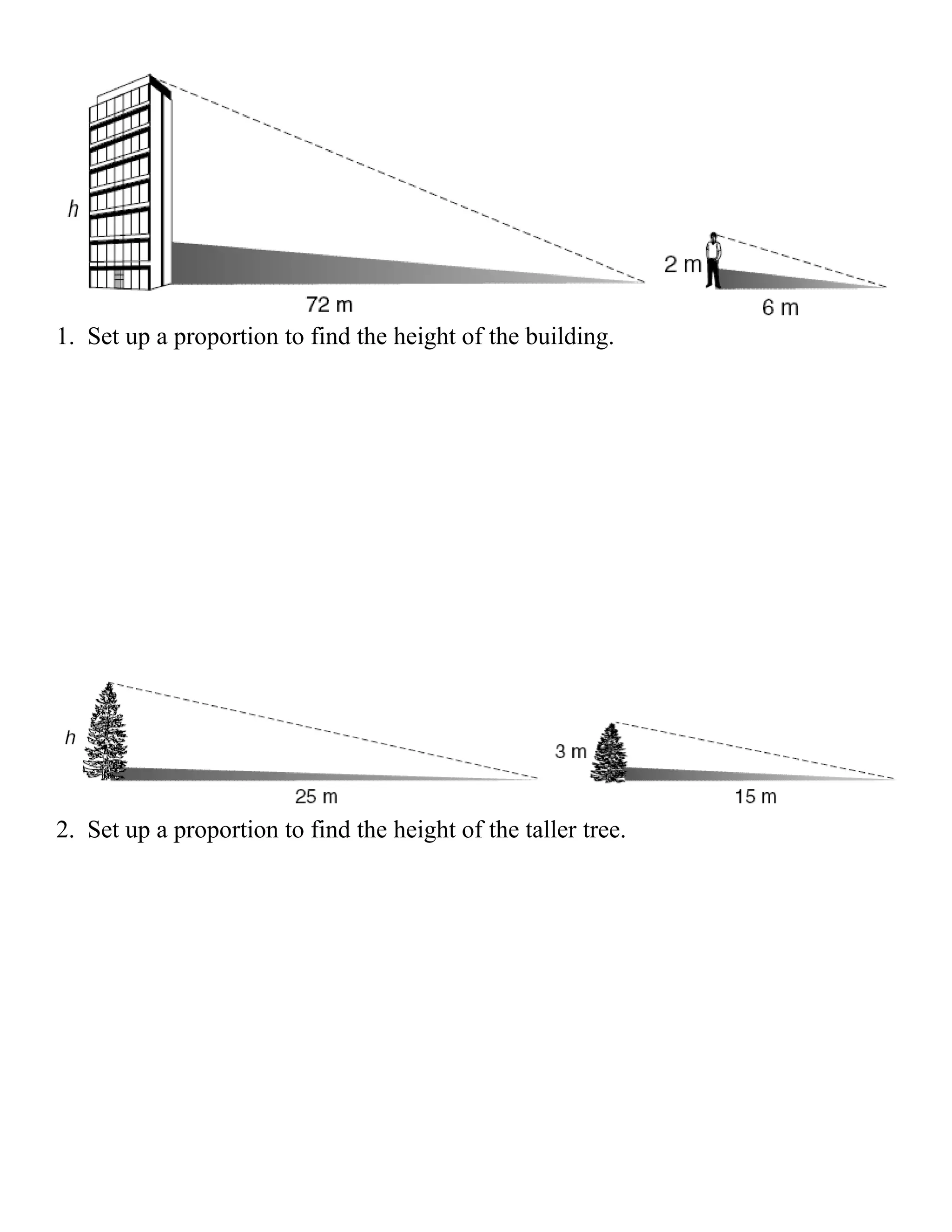
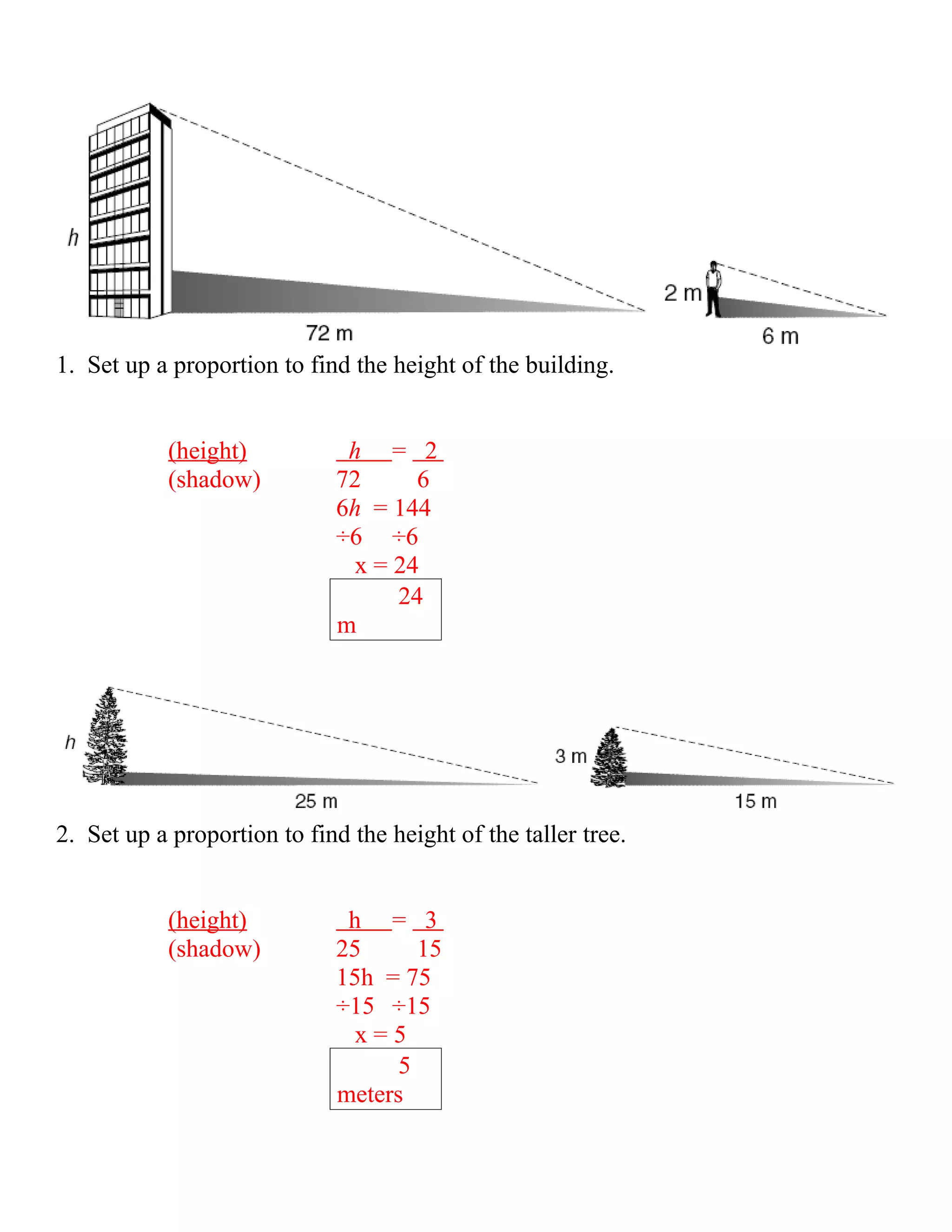
This document contains a lesson on indirect measurement. It defines indirect measurement as using similar figures and proportions to find lengths. It provides an example of using proportions to find the height of a large tree given the height of a small tree and the lengths of their shadows. The document then provides 5 word problems to set up proportions to indirectly find heights or lengths.

1. Name ___________________________________ Date _____________________
Mrs. Labuski / Mrs. Rooney Period _________ Lesson 8-5 Indirect Measure
VOCABULARY DEFINITION EXAMPLE
Indirect See below
Measurement
The small tree is 8 feet high and it casts a 12-foot shadow. The large tree casts a
36-foot shadow. The triangles formed by the trees and the shadows are similar.
So, their heights are proportional. What is the height of the second tree?
To find the height of the large tree, first set up a proportion. Use a variable to stand
for the height of the large tree. Use cross products to solve for x.
__________ = __________

2. 1. Set up a proportion to find the height of the building.
2. Set up a proportion to find the height of the taller tree.

3. 3. A lamppost casts a shadow that is 35 yards long. A 1 yard-tall mailbox casts a
shadow that is 5 yards long. How tall is the lamppost?
4. A 6-foot-tall scarecrow in a farmer’s field casts a shadow that is 21 feet long. A
dog standing next to the scarecrow is 2 feet tall. How long is the dog’s shadow?
5. On a sunny day, a tree casts a shadow that is 146 feet long. At the same time, a
person who is 5.6 feet tall standing beside the tree casts a shadow that is 11.2 feet
long. How tall is the tree?

4. Name ___________________________________ Date _____________________
Mrs. Labuski / Mrs. Rooney Period _________ Lesson 8-5 Indirect Measure
VOCABULARY DEFINITION EXAMPLE
Indirect
measurement
Indirect uses similar See below
Measurement figures and
proportions to
find lengths
The small tree is 8 feet high and it casts a 12-foot shadow. The large tree casts a
36-foot shadow. The triangles formed by the trees and the shadows are similar.
So, their heights are proportional. What is the height of the second tree?
To find the height of the large tree, first set up a proportion. Use a variable to stand
for the height of the large tree. Use cross products to solve for x.
(height) 8 = x
(shadow) 12 36
12x = 288
÷12 ÷12
x = 24
24
feet

5. 1. Set up a proportion to find the height of the building.
(height) h = 2
(shadow) 72 6
6h = 144
÷6 ÷6
x = 24
24
m
2. Set up a proportion to find the height of the taller tree.
(height) h = 3
(shadow) 25 15
15h = 75
÷15 ÷15
x=5
5
meters

6. 3. A lamppost casts a shadow that is 35 yards long. A 1 yard-tall mailbox casts a
shadow that is 5 yards long. How tall is the lamppost?
(height) x = 1
(shadow) 35 5
5x = 35
÷5 ÷5
x=7
x
7 yards
1 yd
35 yd 5 yd
4. A 6-foot-tall scarecrow in a farmer’s field casts a shadow that is 21 feet long. A
dog standing next to the scarecrow is 2 feet tall. How long is the dog’s shadow?
(height) 6 = 2
(shadow) 21 x
6x = 42
÷6 ÷6
x=7
6 ft
2 ft 7 feet
21 feet x
5. On a sunny day, a tree casts a shadow that is 146 feet long. At the same time, a
person who is 5.6 feet tall standing beside the tree casts a shadow that is 11.2 feet
long. How tall is the tree? (height) x = 5.6
(shadow) 146 11.2
11.2x = 817.6
÷11.2 ÷11.2
x x = 73
73 feet
5.6 ft
146 ft 11.2 ft

7. p. 410 #1-7