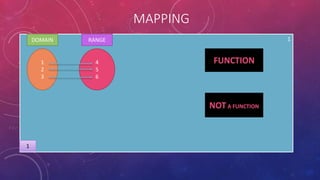
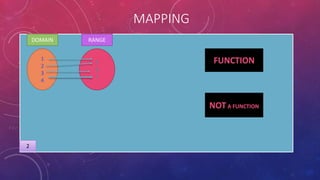
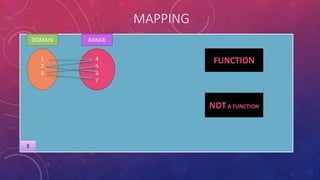
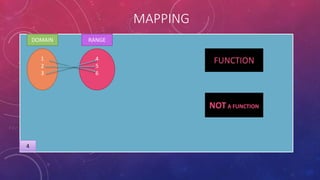
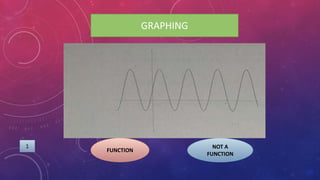
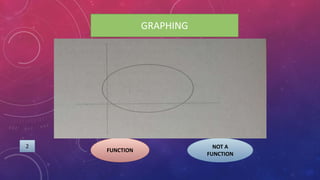
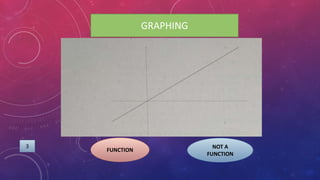
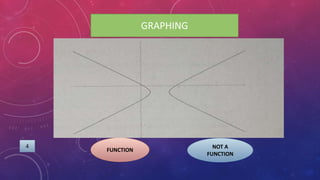
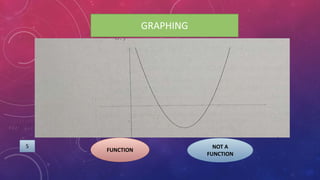
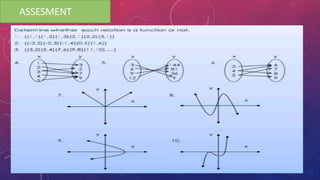
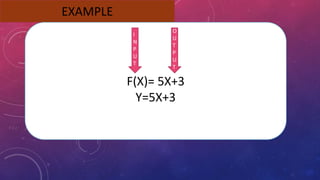
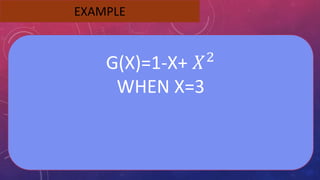The document provides instructions on adding and subtracting functions. It defines how to write the addition and subtraction of two functions F(x) and G(x) as (F+G)(x) and (F-G)(x), respectively. Examples are given to demonstrate evaluating functions using both horizontal and vertical methods. Key steps include changing the sign of the subtrahend for subtraction, and distributing addition/subtraction across all terms for combining like terms. Real-life applications of functions are also briefly mentioned.

1. GENERAL MATHEMATICS 11
LESSON 1- FUNCTIONS

2. PRAYER
COME HOLY SPIRIT FILL THE HEARTS OF THE FAITHFUL AND ENKINDLE IN
THEM THE FIRE OF YOUR DIVINE LOVE. SEND FORTH YOUR HOLY SPIRIT AND
THEY SHALL BE CREATED AND THOUGH SHALL RENEW THE FACE OF THE
EARTH.
LET US PRAY, OH GOD WHO BY THE LIGHT OF THE HOLY SPIRIT DID INSTRUCT
THE HEARTS OF THE FAITHFUL GRANTS US BY THE SAME HOLY SPIRIT TO BE
TRULY WISE AND EVER REJOICE IN ITS CONSOLATION THROUGH CHRIST OUR
LORD. AMEN

3. OBJECTIVES
DETERMINE FUNCTIONS AND RELATIONS
ILLUSTRATE FUNCTIONS THROUGH MAPPING
DIAGRAMS, SETS AND GRAPHS; AND
REPRESENT REAL-LIFE SITUATIONS USING FUNCTIONS

4. Is a rule that relate values from a set of values (domain) to a second
set of values(range)
the set of all x or input values.
pair of objects taken in a specific order.
collection of well- defined and distinct objects, called elements that share a
common characteristic.
the set of all y or output values.
RELATION
DOMAIN
ORDERED PAIR
SET
RANGE
1
5
4
3
2

5. ORDERED PAIR
(1,4)

6. DOMAIN
{(1,8) ,(2,6),(3,9)}

7. RANGE
{(1,8) ,(2,6),(3,9)}

8. FUNCTION
A FUNCTION IS A RELATION WHERE EACH
ELEMENT IN THE DOMAIN IS RELATED TO ONLY
ONE VALUE IN THE RANGE BY SOME RULE

9. MAPPING
DOMAIN RANGE
A
B
C
1
2
3
SETS
{(2,4), (3,6),(4,8),(5,10)}
GRAPHING

10. GRAPHING
V L T
VERTICAL LINE TEST
INTERSECT THE
GRAPH ONLY ONCE

11. MAPPING
1
DOMAIN RANGE
1
2
3
4
5
6
FUNCTION
NOTA FUNCTION
1

12. MAPPING
DOMAIN RANGE
1
2
3
4
5
6
7
FUNCTION
NOTA FUNCTION
2

13. MAPPING
DOMAIN RANGE
1
2
3
4
5
6
7
FUNCTION
NOTA FUNCTION
3

14. MAPPING
DOMAIN RANGE
1
2
3
4
5
6
FUNCTION
NOTA FUNCTION
4

15. SETS
{ (1,2),(2,3), (3,5),(4,7)}
FUNCTION
NOT A
FUNCTION
1

16. SETS
{ (1,3),(1,4), (2,5),(2,6), (3,7)}
FUNCTION
NOT A
FUNCTION
2

17. SETS
{ (1,3),(2,6), (3,9),(4,12), (5,14)}
FUNCTION
NOT A
FUNCTION
3

18. GRAPHING
FUNCTION
NOT A
FUNCTION
1

19. GRAPHING
FUNCTION
NOT A
FUNCTION
2

20. GRAPHING
FUNCTION
NOT A
FUNCTION
3

21. GRAPHING
FUNCTION
NOT A
FUNCTION
4

22. GRAPHING
FUNCTION
NOT A
FUNCTION
5

23. FUNCTIONS IN REAL LIFE
CIRCUMFERENCE OF A
CIRCLE
C(d) = d𝜋

24. FUNCTIONS IN REAL LIFE
A SHADOW
A FUNCTIONS OF ONE’S
HEIGHT

25. FUNCTIONS IN REAL LIFE
DRIVING A CAR
LOCATION IS A FUNCTION OF TIME

26. REMEMBER
A RELATION IS A FUNCTION WHEN EVERY X- VALUE IS ASSOCIATED TO ONLY
ONE Y-VALUE
YOU CAN ILLUSTRATE FUNCTIONS THROUGH GRAPHING, MAPPING OR SETS
FUNCTIONS CAN BE SEEN IN OUR DAILY LIVES LIKE DRIVING A CAR, LENGTH OF
SHADOWS AND MANY MORE

27. ASSESMENT

28. ASSIGNMENT
YOU WILL WORK ON THE ASSESMENT
ON THE MODULE 1

29. GEGG
GENERAL MATHEMATICS
LESSON 2: EVALUATION OF FUNCTIONS

30. OBJECTIVES
SUBSTITUTE VALUES IN A FUNCTION;
EVALUATE FUNCTION

31. INPUT

32. “RULE”

33. ‘’ F(X)=… “READ AS F OF X”
G(X), H(X) AND OTHER LETTERS

34. EXAMPLE
F(X)= 5X+3
Y=5X+3
I
N
P
U
T
O
U
T
P
U
T

35. EXAMPLE
F(X)= 5X+3 WHEN X=4
FIND F(4) IF F(X)=5X+3

36. HOW TO EVALUATE A FUNCTION
F(X)=5X+3, WHEN X=4
1.F(X)=5X+3COPY THE GIVEN
2.F(4)=5(4)+3REPLACE X WITH 4 AND PERFORM THE OPERATION
3.F(4)=20+3PERFORM THE INDICATED OPERATION
4.F(4)=23

37. EXAMPLE
G(X)=1-X+ 𝑋2
WHEN X=3

38. EXAMPLE
G(X)=1-X+ 𝑋2
WHEN X=3
1. G(X)=1-X+ 𝑋2
COPY THE GIVEN
2. G(3)=1-3+ (3)2
REPLACE X WITH 3 AND PERFORM THE
INDICATED OPERATION
3. G(3)=1-3+9 PERFORM THE INDICATED OPERATION
4. G(3)=7

39. REMEMBER
THE CLASSIC WAY OF WRITING A FUNCTION IS ‘’F(X)=…”
TO EVALUATE A FUNCTION IS TO REPLACE F SUBSTITUTE ITS VARIABLES WITH A
GIVEN NUMBER OF EXPRESSIONS.
IT IS RECOMMENDED PUTTING THE SUBSTITUTED VALUES INSIDE THE
PARENTHESES ( ), SO YOU DON’T MAKE MISTAKES.

40. ASSESMENT

41. ASSIGNMENT
YOU WILL WORK ON THE ASSESMENT
ON THE MODULE 2

42. OPERATIONS OF FUNCTIONS
ADDITION AND SUBTRACTION

43. OPERATION OF FUNCTIONS
ADDITION OF FUNCTIONS

44. OBJECTIVES
FOLLOW THE STEPS IN ADDING FUNCTIONS
ADD FUNCTIONS

45. ADDITION OF INTEGERS
RULE 1: The sum of two positive integers is a positive integer.
2+9=11
RULE 2: The sum of two negative integers is a negative integers is a negative
integer. -2+-9= -11
RULE 3: if the signs are different, subtract the numbers and use the sign of the
larger number. -2 +9= 7

46. How to add functions?
F(x) g(x)
F(x) + g(x) or we can use this
(f+g) (x)
Read as ‘’f plus g of x”

47. EXAMPLE:
F(X)+G(X) OR (F+G) (X)
F(X)= 3X+2
G(X)=4-5X
MEHOD 1: HORIZONTAL
(F+G) (X)=(3X+2)+(-5X+4)
(F+G)(X)=3X+2+(-5X)+4
(F+G)(X)=3X+(-5X)+2+4
(F+G)(X)=-2X+6

48. EXAMPLE:
F(X)+G(X) OR (F+G) (X)
F(X)= 3X+2
G(X)=4-5X
MEHOD 1: VERTICAL
(F+G) (X)=3X+2
-5X+4
-2X+6
OR -2(X-3)

49. EXAMPLE:
F(X)+G(X) OR (F+G) (X)
F(X)= 4X+2𝑋2
-2
G(X)=4-3X
MEHOD 1: VERTICAL
(F+G) (X)= 2𝑋2
+4X-2
-3X+4
2𝑋2
+X+2

50. EXAMPLE:
F(X)+G(X) OR (F+G) (X)
F(X)= 4X+2𝑋2
-2
G(X)=4-3X
MEHOD 2: HORIZONTAL
(F+G) (X)= 2𝑋2
+4X-2)+(-3X+4)
(F+G)(X)=2𝑋2
+4X-2+(-3X)+4)
(F+G)(X)=2𝑋2
+4X+(-3X)-2+4
(F+G)(X)= 2𝑋2
+X+2

51. Assessment:

52. Operation of functions
SUBTRACTION OF FUNCTIONS

53. OBJECTIVES
FOLLOW THE STEPS IN SUBTRACTING FUNCTIONS.
SUBTRACTION OF INTEGERS

54. SUBTRACTION OF INTEGERS
RULE: CHANGE THE SIGN OF THE SUBTRAHEND AND FOLLOW THE
RULES FOR ADDTITION

55. SUBTRACTION OF INTEGERS
KEEP CHANGE CHANGE
5-17
5+(-17)=-12

56. F(X) G(X)
F(X)-G(X)
(F-G)(X)
F(X)=3X+2
G(X)=4-5X
EXAMPLE

57. HORIZONTAL METHOD
1. (F-G)(X)=(3X+2)-(4-5X)
2. (F-G)(X)= 3X+2+(5X-4)
3. (F-G)(X)= 3X+2+5X-4
4. (F-G)(X)=3X+5X+2-4
5. (F-G)(X)=8X-2
EXAMPLE

58. VERTICAL METHOD
(F-G)(X)= 3X+2
5X-4
8X-2
OR
2(4X)-(2)(1)
2(4X-1)
EXAMPLE

59. FIND (F-G)(X)
F(X)=4X+ 2𝑋2
-2
G(X)=4-3X
1. (F-G)(X)=(4X+ 2𝑋2
-2)-(4-3X)
2. (F-G)(X)=(2𝑋2
+4X-2+(3X-4)
3. (F-G)(X)=(2𝑋2
+4X+3X-2-4
4. (F-G)(X)=2𝑋2
+7X-6
EXAMPLE

60. FIND (F-G) (X) USING THE TWO FUNCTIONS GIVEN IN
EACH NUMBER
1.F(X)=3X+3 , G(X)=-4X+1
2.F(X)=2X+5 , G(X)=4𝑋2
+2X-2
3.F(X)= 5X+1, G(X)= 3X-2
4. F(X)= -15 𝑋2
-2X+5, G(X)=3 𝑋2
+X-7
5.F(X)=3 𝑋2
-2X+1, G(X)= 4 𝑋2
+5X-4
ASSESSMENT