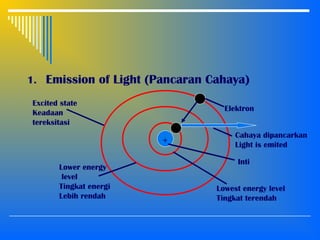
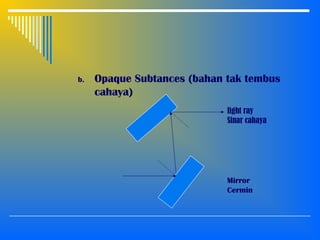
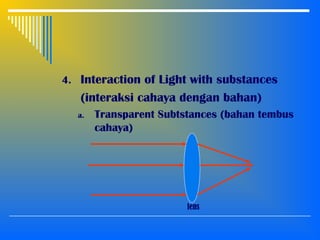
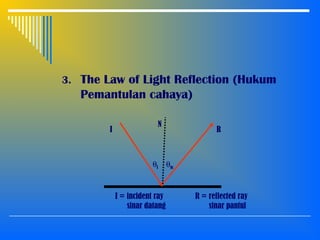
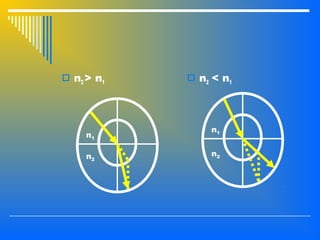
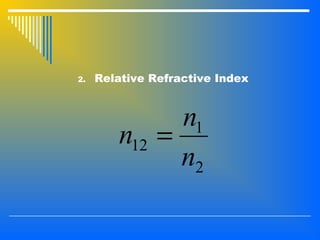
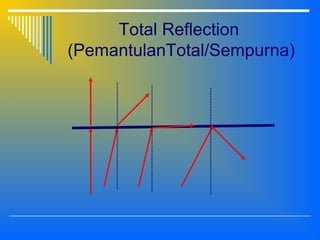
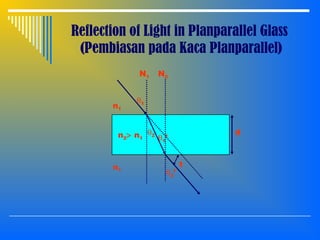
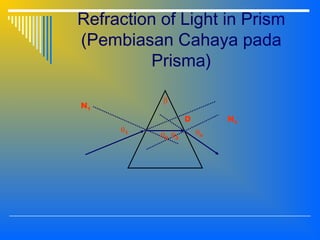
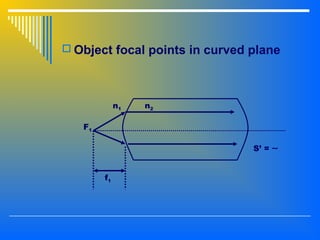
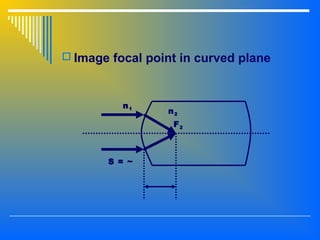
GelombanG dan optika discusses key concepts in optics including: 1. The nature of light as both waves and particles. Light exhibits properties of waves like interference and diffraction as well as particle properties demonstrated by the photon model. 2. The interaction of light with materials including reflection, refraction, and total internal reflection. Reflection and refraction follow Snell's laws which relate the angle of incidence and refraction based on the refractive indices of the materials. 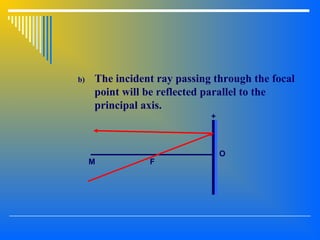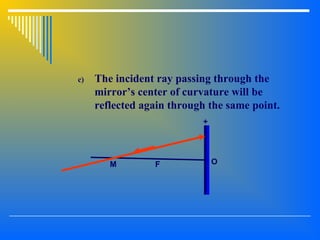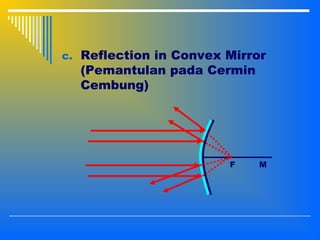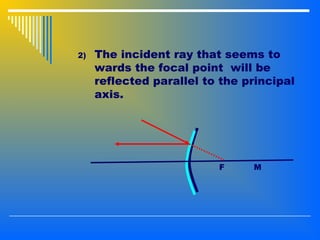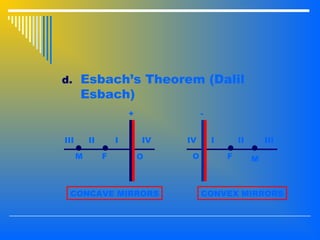3. Image formation using plane mirrors, convex and concave spherical mirrors which can be analyzed using ray diagrams and mirror equations. The characteristics and magnification of images depend on the type of mirror and position of the object.

1. GelombanG dan optika

2. Keywords
(kata kunci)
 Ligght theory (teori cahaya)
 Reflection of light
(pemantulan cahaya)
 Mirror (cermin)
 Mirror equation (persamaan
cermin)
 Image formation
(pembentukan bayangan)
 Refraktion of light
(pembiasan cahaya)
 Refractive index (indeks bias)
 Lens (lensa)
 Lens equation (persamaan
lensa)
 Optical instruments (alat-alat
optik)
 Electromagnetic waves
spectrum (spektrum
gelombang elektromagnetik)

3. A. Nature of Light (sifat dasar cahaya)
Sifat cahaya ada dua, yaitu:
1. Cahaya sebagai gelombang (waves)
2. Cahaya sebagai partikel (particles)

4. 1. Emission of Light (Pancaran Cahaya)
Elektron
Cahaya dipancarkan
Light is emited
Inti
Excited state
Keadaan
tereksitasi
Lower energy
level
Tingkat energi
Lebih rendah
Lowest energy level
Tingkat terendah
+

5. 2. Electromagnetic Waves (gelombang
Elektromagnetik)
Cahaya polikromatik (polychromatic light)
adalah cahaya yang terdiri dari berbagai
panjang gelombang dan frekuensi.
contoh : cahaya matahari (sunshine)
cahaya monokramatik (monochromatic light)
adalah cahaya yang hanya terdiri dari satu
panjang gelombang dan frekuensi.
contoh : laser

6.  Hubungan panjang gelombang dan frekuensi
gelombang elektromagnetik (EMG),
dirumuskan:
fcv λ==

7.  Dengan:
 v = c = light speed (laju cahaya)
= 3 x 108
m/s
 λ = wavelength/panjang gelombang (m)
 f = frequency/frekuensi (Hz)

8. 3. Photon (foton)
adalah paket-paket energi cahaya atau
energi yang dibangkitkan oleh gerakan
muatan-muatan listrik (radiasi
elektromagnetik)
Foton merupakan partikel-partikel yang
tidak bermuatan listrik dan tidak
bermassa,tetapi mempunyai energi dan
momentum.

9.  Besarnya energi
sebuah foton
dirumuskan:
 Dengan :
 E = photon energy (J)
 h = Planck’s constant
 = 6,63 x 10-34
Js
 f = frequency (Hz)
 1 eV = 1,6 x 10-19
J
hfE =

10. Contoh soal
 Calculate the amount of photon emitted by a 100 watt
lamp in 2 second, if the light that radiated by the lamp
has wavelength of 600 nm!
 Diket :
 P = 100 watt t = 2 s
 λ = 600 nm = 600 x 10-9
m
 c = 3 x 108
m/s
 h = 6,63 x 10-34
Js
 Ditanya: n

11. b. Opaque Subtances (bahan tak tembus
cahaya)
light ray
Sinar cahaya
Mirror
Cermin

12. 4. Interaction of Light with substances
(interaksi cahaya dengan bahan)
a. Transparent Subtstances (bahan tembus
cahaya)
lens

13. c. Translucent Substances (bahan buram)
- meneruskan
- memantulkan
- menyerap
- menghamburkan
contoh : air keruh

14. 5. Interference, Diffraction, and
Polarization (interferensi, difraksi, dan
polarisasi)
a. Interference (Interferensi)
adalah sebuah peristiwa yang terjadi
ketika dua buah gelombang bertemu
pada saat bergerak dalam medium yang
sama.
Interferensi gelombang ada 2 yaitu:
interferensi konstruktif dan destruktif

15. b. Difraction (difraksi)
Pembelokan atau penyebaran gelombang cahaya ketika
cahaya tersebut dilewatkan melalui celah sempit.
contoh : difraksi sinar – x oleh kisi kristal padat
c. Polarization
proses pengubahan cahaya tak terpolarisasi menjadi
cahaya terpolarisasi.
Proses polarisasi:
- transmisi
- pemantulan
- pembiasan
- hamburan menggunakan polaroid filter.

16. 6. The development of Theories of Light
(Perkembangan Teori-teori Cahaya)
a. Impuls Theory of Light (teori impuls
cahaya)
b. Corpuscular Theory (teori Korpuskuler)
c. Waves Theory (teory gelombang)
d. Theory of Electromagnetic Waves (teori
gelombang elektromagnetik)
e. Quantum Theory (teori kuantum)

17. B. Reflection of Light (Pemantulan Cahaya)
1. Stremam of Ligth (Berkas cahaya)
Source of light
Sumber cahaya
Waves front
Muka gelombang
Rays/sinar

18.  Kinds of stream of ligth (jenis-jenis berkas
cahaya)
Parallel/sejajar
Diverging
Menyebar
Converging
mengumpul

19. 2. Types of Light Reflection (jenis-jenis
pemantulan cahaya)
Specular Reflection
(smooth surfaces)
Diffuse Reflection
(rough surfaces

20. 3. The Law of Light Reflection (Hukum
Pemantulan cahaya)
I R
θi θR
N
I = incident ray
sinar datang
R = reflected ray
sinar pantul

21.  The Law of light reflection:
a. Incident ray, reflected ray, and the
normal line cut at one point and lie on
one straight plane.
b. The angle of incidence (θi) is equal to the
angle reflection (θR)
θI = θR

22. 4. Reflection of Light on Plane Mirrors
(Pemantulan pada Cermin Datar)
a. The Characteristics of Image on Plane
Mirrors (Sifat-sifat Bayangan pada
Cermin Datar)
1) Cannot catched by screen (virtual image)
(bayangan maya)
2) Upright and face invertedly to the object
(tegak dan menghadap berlawanan arah
terhadap bendanya)

23. 3) The image is equal in size as the object
(bayangan sama besar dengan bendanya)
4) The image distance to the mirror is equal
to the object distance to the mirror (jarak
bayangan ke cermin sama dengan jarak
benda ke cermin)
S S’

24. b. Drawing Image Formation in Plane
Mirrors with Ray Diagram (melukis
pembentukan bayangan pada cermin
datar dengan diagram sinar)
c. The Sum of Image on Plane Mirror
(jumlah bayangan pada cermin
datar)
mn −=
α
0
360

25. Contoh
 Two plane mirrors form an angle of
90o
of each. If an object is placed
between both mirrors, determine the
sum of image formed!

26. 5. Reflection in Curved Mirrors
(Pemantulan pada cermin Lengkung)
a. The Anatomy of Concave and
Convex Mirror (anatomi cermin
cekung dan cermin cembung)
O
FM
O
F M
R R
Concave mirror Convex mirror

27. b. Reflection in Concave Mirrors
(Pemantulan Pada Cermin Cekung)

28. 1) Special Rays in Convave Mirrors (sinar-
sinar istimewa pada cermin cekung)
a) The incident ray parallel to the principal
axis will be reflected passing through the
focal point.
O
FM
+

29. b) The incident ray passing through the focal
point will be reflected parallel to the
principal axis.
O
FM
+

30. c) The incident ray passing through the
mirror’s center of curvature will be
reflected again through the same point.
OFM
+

31. 2) Drawing Image Formation in Concave Mirrors
with Ray Diagrams (melukis pembentukan
bayangan pada cermin cekung dengan
diagram sinar)
3) Spherical Aberration (Aberasi Sferis)
FM

32. c. Reflection in Convex Mirror
(Pemantulan pada Cermin
Cembung)
F M

33. 1) Special Rays in convex Mirrors
(Sinar-sinar Istimewa pada
Cermin Cembung)
a) The incident ray parallel to the
principal axis will be reflected as
if it comes from the focal point.
F MO

34. 2) The incident ray that seems to
wards the focal point will be
reflected parallel to the principal
axis.
F M

35. c) The incident ray that seems to
wards the mirror’s center of
curvature will be reflected as if it
comes from that point.
F M

36. 2) Drawing Image Formation in
Convex Mirrors with Ray
Diagram (Melukis
Pembentukkan Bayangan pada
Cermin Cembung dengan
Diagram Sinar)

37. d. Esbach’s Theorem (Dalil
Esbach)
OFM
III II I IV
+
CONCAVE MIRRORS
O F M
IV I II III
-
CONVEX MIRRORS

38.  The image characteristics of concave and
convex mirrors can be determined based on
Esbach’s theorem according to the rules as
follows:
1. R + R’ = 5
2. All images in front of the mirrors are real and
inverted.
3. All images behind the mirrors are virtual and
upright.
4. R’ > R (then the image is magnified)
5. R’ < R (then the image is reduced)

39. e. The Curved Mirror Equation
(Persamaan Cermin Lengkung)
'
112
'
111
ssR
atau
ssf
+=
+=

40.  Where:
 f = mirror focal length (panjang
fokus cermin)
 S = object distance to the mirror
(jarak benda ke cermin)
 S’= image distance to the mirror
(jarak bayangan ke cermin)
 R = mirror’s radius of vurvature
(jari-jari cermin)
= 2f

41.  Note (catatan)
 In the curved mirror equation, there
are rules of mark, those are:
 f and R is positive (+) for concave
mirrors
 f and R is negative (-) for convex mirrors
 S is positive (+) if the object is in front
of the mirror and s is negative (-) if the
object lies behind the mirror.
 S’ is positive (+) if the image lies is in
front of the mirror and s’ is negative (-)
if the image lies behind the mirror.

42.  Linear magnification is defined
as the ratio of image height (h’)
with object height (h), this
magnification is formulated by
the following equation.
s
s
h
h
M
'' −
==

43.  Where:
 M = linear magnification
(perbesaran linier)
 h’ = image height (tinggi
bayangan)
 h = object height (tinggi benda)

44. Sample Problem
1. A convex mirror has focal
length of 20 cm. If an object lies
10 cm in front of the mirror,
determine:
a. Image distance to the mirror
b. Image linier magnification.

45. 2. An object of 2 cm in height
stands upright in front of a
concave mirror which has the
focal length 10 cm. If the object
distance to the mirror 15 cm,
ditermine:
a. Image magnification
b. Image height

46. f. Problem Solving of Two Mirrors
which Face Each Other
(Penyelesaian Masalah Dua
Buah Cermin yang saling
Berhadapan)
Secara matematis jarak antar
cermin dirumuskan:
2
'
1 ssd +=

47.  Where:
 d = distance between mirror (jarak
antar cermin)
 s1’ = first image distance to the
first mirror (jarak bayangan
pertama ke cermin pertama)
 S2 = first image distance to the
second mirror (jarak
bayangan pertama ke cermin
ke dua)

48.  The final image resulthan from
the curved mirror system that
face each other has the total
magnification as follows.
2
'
2
1
'
1
21
s
s
x
s
s
xMMMtot ==

49. Refraction of Light
(Pembiasan Cahaya)
1. The Definition of Light
Refraction (Pengertian
Pembiasan Cahaya)
Pembiasan cahaya adalah:
peristiwa pembelokan arah
cahaya ketika meliwati bidang
batas diantara dua medium
yang berbeda.

50.  Pada Pembiasan cahaya terjadi:
 Perubahan arah
 Perubahan kecepatan
 Perubahan panjang gelombang
 Frekuensi dan fase gelombang
tetap

51. 2. The Law of Refraction (Snell’s Law)
1. Snell’s I law:
“The incident ray, refracted ray and
normal line all lie on one plane”
2. Snell’s II law:
“If the incident ray travels from a less
dense to a denser medium, then it
bends (refracts) towards the normal
line, and if the incident ray travels from
a denser to a less dense medium then it
bends (refracts) away from the normal
line.

52.  n2 > n1
n2
n1
 n2 < n1
n1
n2

53.  Secara matematis dirumuskan:
2211 sinsin θθ nn =
Where:
n1 = refractive index of medium 1
n2 = refractive index of medium 2
Θ1 = angle of incidence
Θ2 = angle of refraction

54. 3. Refractive Index (Indeks Bias)
1. Absolute refractive index
v
c
n =
Where:
n = absolute refractive index
c = light speed in air
= 3 x 108
m/s
v = light speed in medium (m/s)

55. 2. Relative Refractive Index
2
1
12
n
n
n =

56.  Generally, for two medium, the
Snell’s law equation is:
21
2
1
1
2
2211
sin
sin
sinsin
n
n
n
or
nn
==
=
θ
θ
θθ

57.  When light travels a certain
medium to another medium and
is refracted, then it has different
speed in the two medium.
Therefore, holds the following
eqution.
21
2
1
1
2
2
1
n
n
n
v
v
===
λ
λ

58. Sample Problem
 A stream of light travels from air to a
glass with the angle of incidence 60o
,
if nair = 1 and nglass = √3, determine the
angle of light refraction!
 The speed of light in air 3 x 108
m/s
and its frequency 6 x 1014
Hz,
determine:
a. Light speed in water (n = 1,33)
b. The change of wavelength in water and
in air

59. Scientific Activity
(Kegiatan Ilmiah)
 Refraction of Light in Planparallel Glass
( Pembiasan cahaya pada kaca Planparalel)
 Refraction of Light in Prism
(Pembiasan Cahaya pada Prisma)

60. Total Reflection
(PemantulanTotal/Sempurna)

61.  Total reflection can occur if the following two
conditions are complied, those are, light
travels from a denser to a less dense medium
and the light angle of incidence is larger than
the critical angle.
1
2
21
sin
90sinsin
n
n
nn
k
o
k
=
=
θ
θ

62.  Where :
 n1 = refractive index of medium 1 (denser
medium)
 n2 = refractive index of medium 2 (less dense
medium)
 θk = critical angle

63. Reflection of Light in Planparallel Glass
(Pembiasan pada Kaca Planparallel)
N1 N2
d
n1
n2> n1
n1
θ1
θ2
t
θ1’
θ2’

64.  The magnitude of light displacement complies
the following equation:
( )
2
21
cos
sin
θ
θθ −
=
d
t

65.  Where:
 t = displacement of light
 d = planparallel glass thickness
 θ1= angle of incidence
 θ2= angle of refraction

66. Refraction of Light in Prism
(Pembiasan Cahaya pada
Prisma)
N1
N2
β
θ1
θ2 θ3
θ4
D

67.  Based on the figure above, then the
refraction in prism the following
equations:
βθθ
θθβ
−+=
+=
41
32
D
and
Where:
β = angle of refrator
θ1 = first angle of
incidence
θ2 = first angle
Of refraction
D = deviation angle
θ3 = second angle of
Incidence
θ4 = second angle of
refraction

68.  If θ1 = θ4, then:
βθ −= 12mD
Dm = angle of minimum deviation

69.  Because at the moment of minimum
deviation θ1 = θ4, then θ2= θ3, so that θ1= ½
(β + Dm), and β = 2θ2 = 2θ3
 Then, Snell’s law equation:
( ) ββ 2
1
2
1
sinsin pmm nDn =+
Where :
nm = refractive index of medium
np = refractive index of pris

70.  Specifically for β ≤ 150
, then holds the
following equation :
β





−= 1
m
p
m
n
n
D

71. Sample problem
 The ray of light shown in Figure 1 is
incident upon a 600
-600
-600
glass prism, n
= 1,5
θ1=450
θ2 θ1’
θ2’
600
600
600
P Q

72. a. Using Snell’s law of refraction,
determine the angle θ2, the nearest
degree.
b. Using elementary geometri, determine
the value of θ1’
c. Determine θ2’

73.  A light hits one surface of a thick glass
by angle of incidence 600
. If the
refraction index of glass 1,5, then
calculate the angle formed by the light
coming out from the glass to the normal
line!

74. Refraction of Light in Curved Plane
(Pembiasan Cahaya pada Bidang Lengkung)
 Light refraction in curved plane
s
S’
n1 n2

75.  Mathematically, the image formation
in transparent curved plane complies
the following equation:
R
nn
s
n
s
n 12
,
21 −
=+
Where:
n1 = refractive index of medium 1
n2 = refractive index of medium 2
S = object distance to the curved plane surface
S’ = image distance to the curved plane surface
R = radius of curvature

76.  While the magnification of image
formed can be ditermined by the
following equation:
2
1''
n
n
x
s
s
h
h
M ==
Where:
M = image magnification
h’ = image height
h = object height

77.  The value of R, s and s’ from the
above equtions comply the following
rules:
 R positive (+) if the surface of plane is
convex and R negative (-) if the surface
of plane is concave.
 S positive (+) for real object and s
negatif (-) for virtual object.
 S’ positive (+) for real image and s’
negatif (-) for virtual image.

78.  Object focal points in curved plane
F1
f1
n1 n2
S’ = ∼

79.  Based on the figure above, for s = f1,
then s’= ~, therefore the object focal
length (f1) can be determined as
follows:
12
1
1
1
12
1
121
1221
,
nn
Rn
f
thenfs
because
nn
Rn
s
R
nn
s
n
R
nnn
s
n
−
=
=
−
=
−
=
−
=
∝
+
Where:
f1 = object focal
length

80.  Image focal point in curved plane
n1
n2
F2
S = ~

81. 12
2
2
nn
Rn
f
−
= Where:
f2 = image focal
length