Lecture 37 som 07.05.2021
•
0 likes•26 views
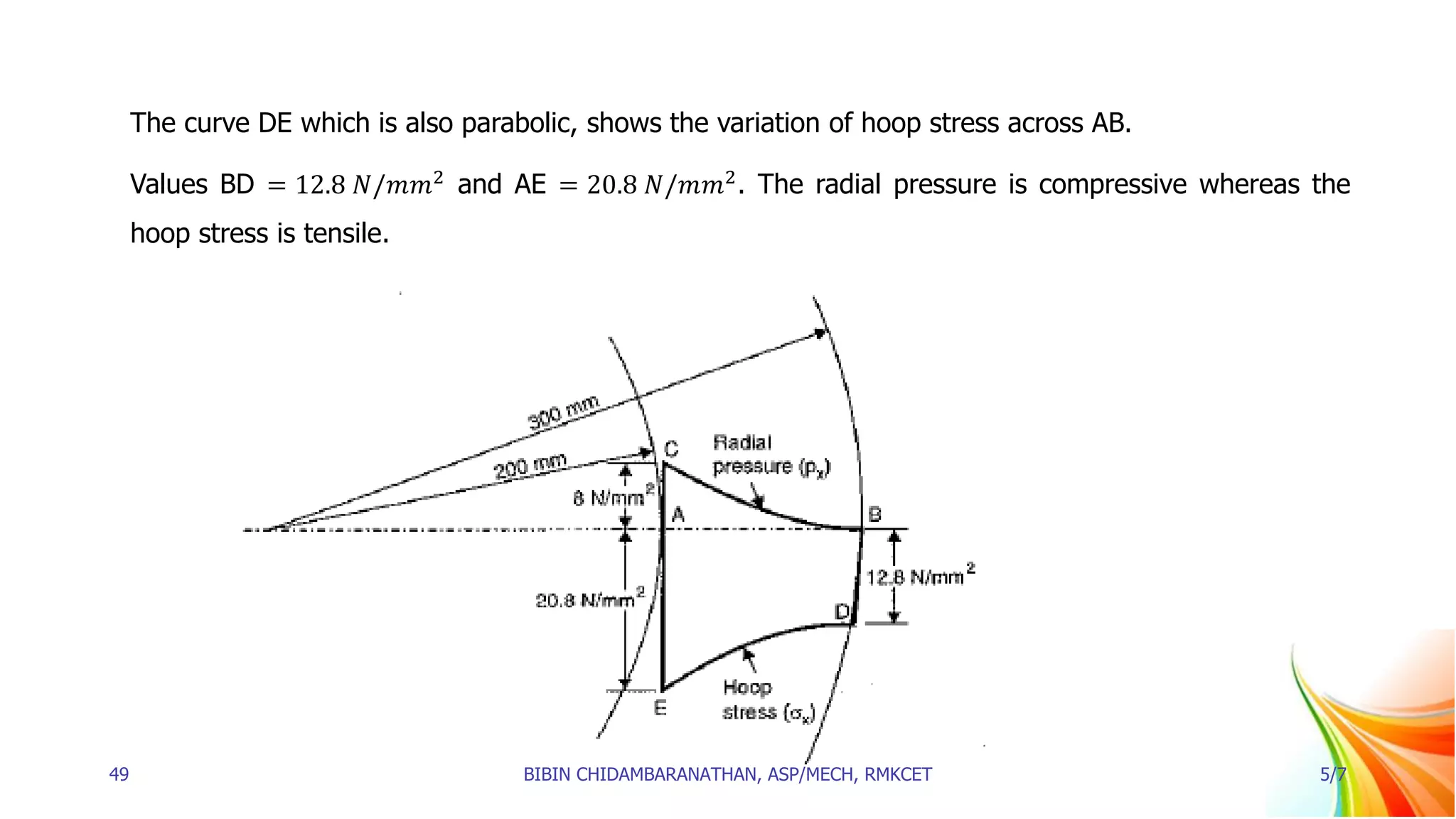
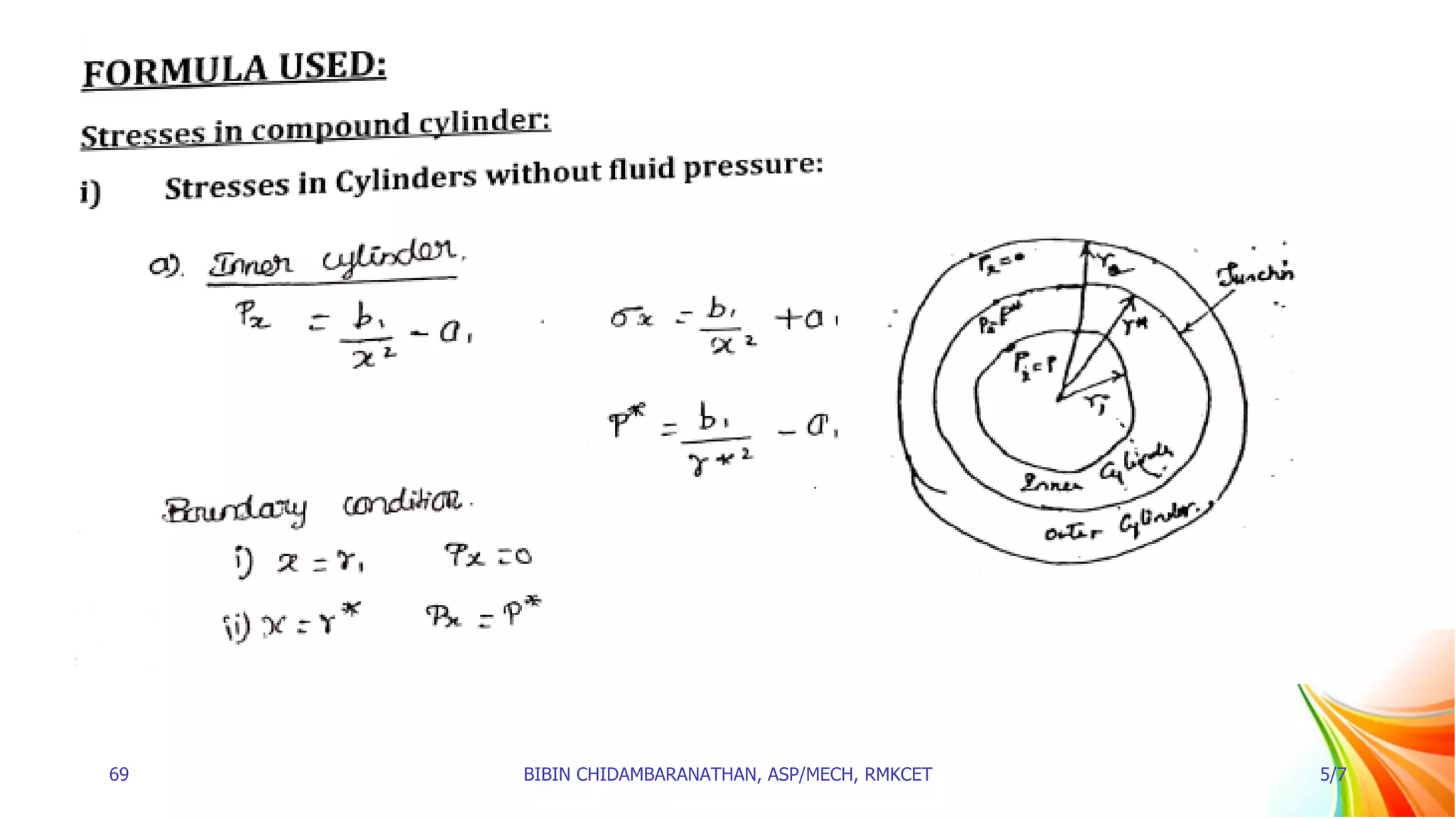
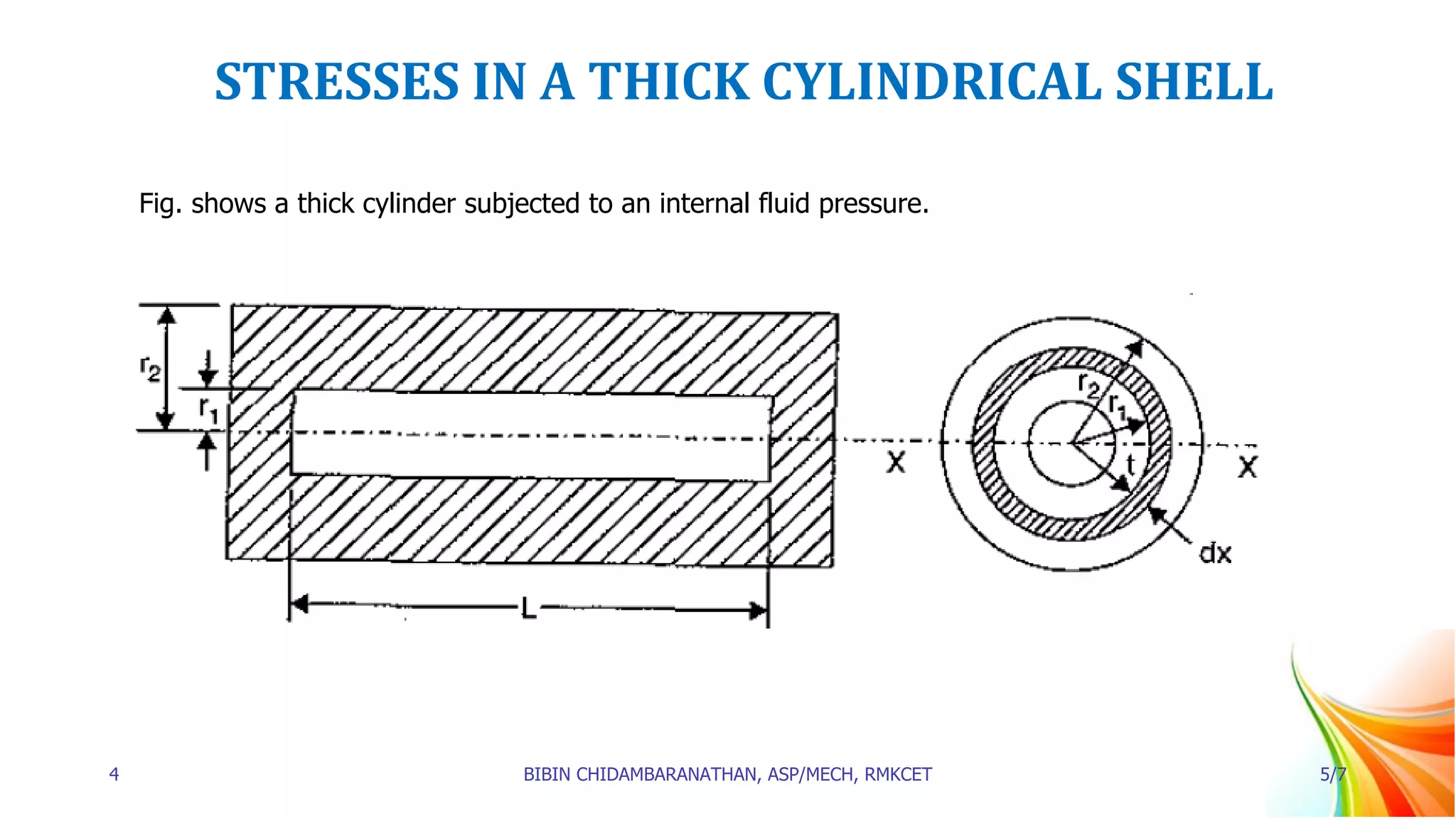
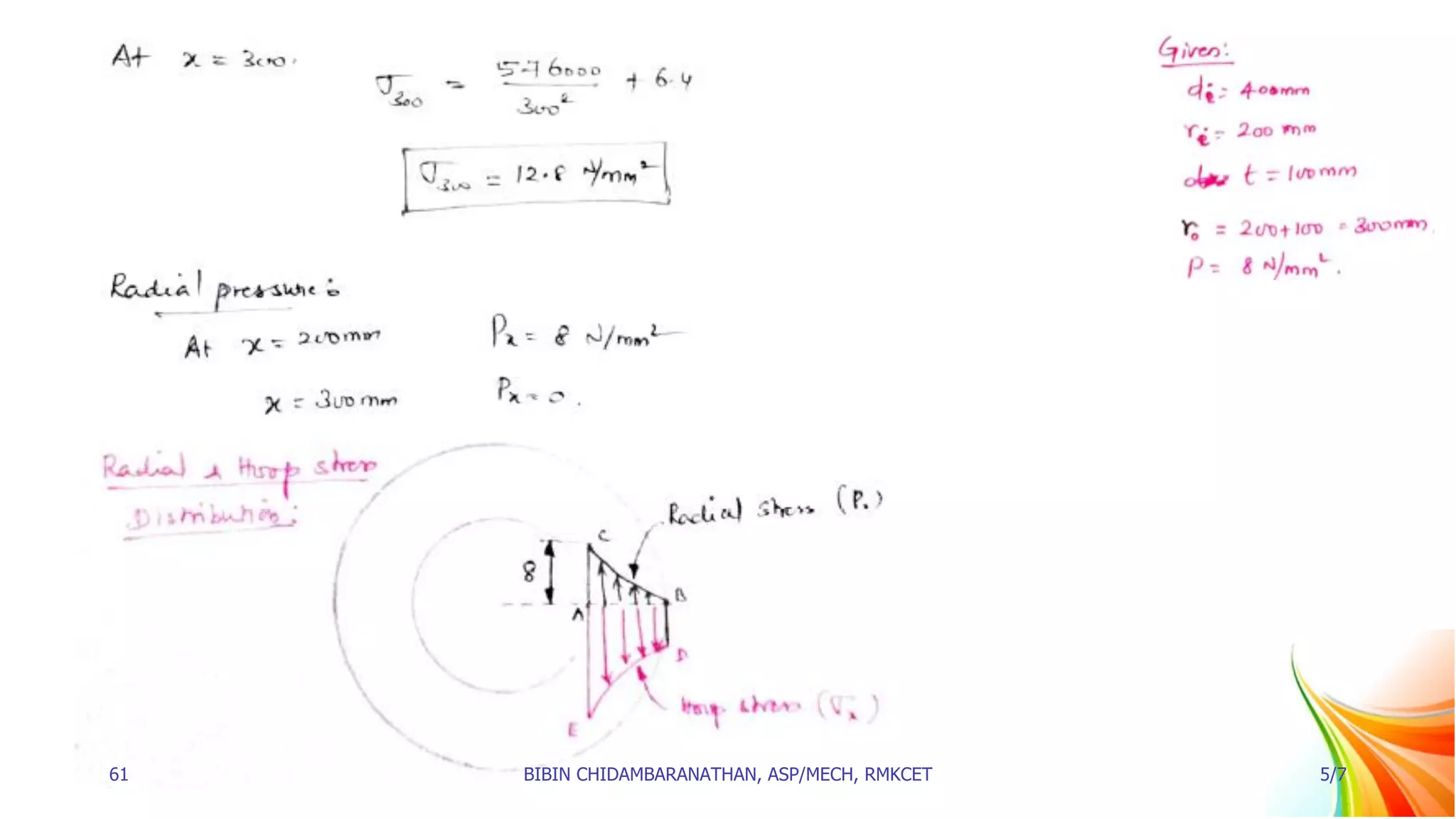
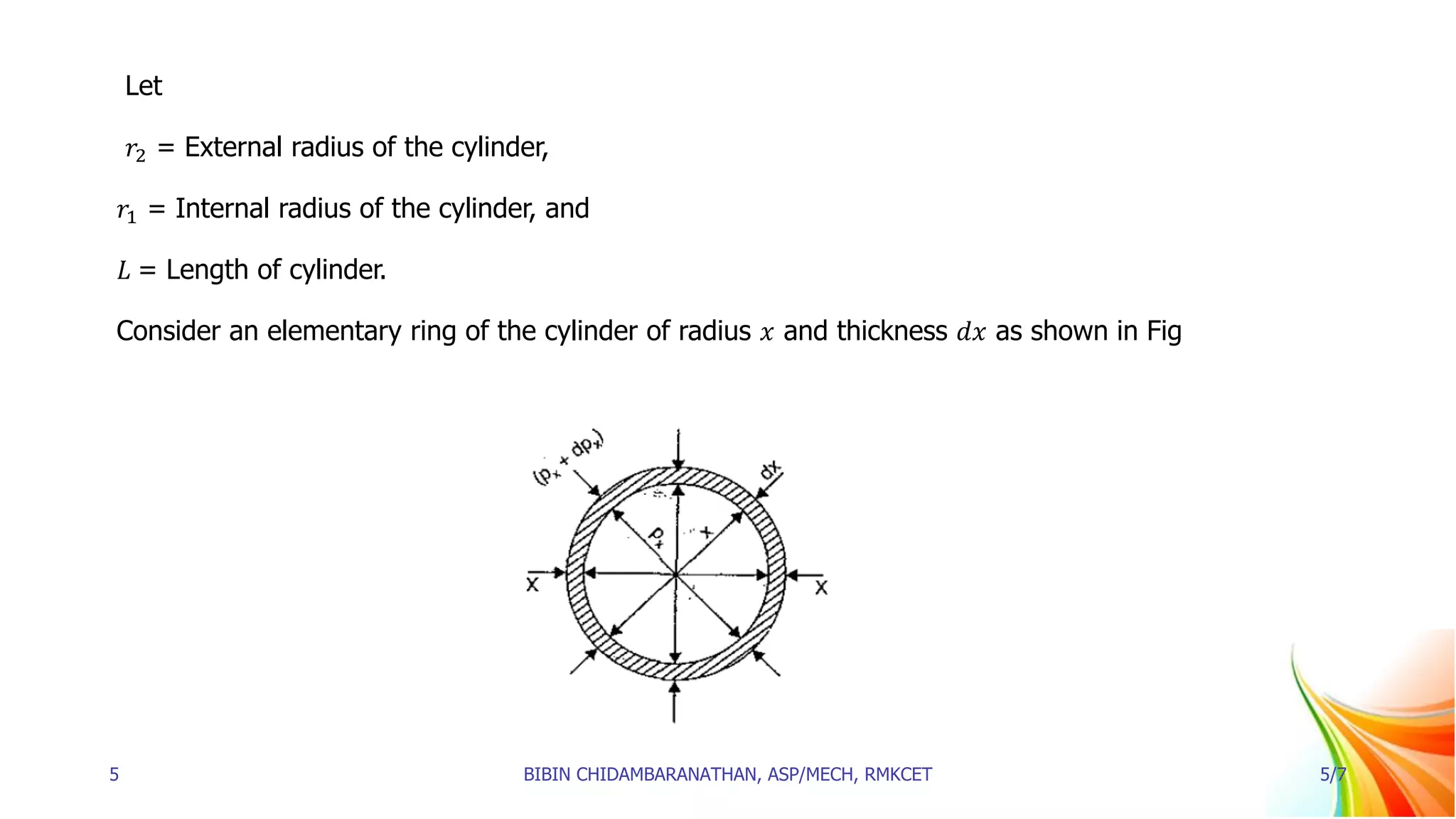
1. Thick cylinders are defined as cylinders where the ratio of thickness to internal diameter is greater than 1/20. For thick cylinders, the hoop stress varies across the thickness from a maximum at the inner circumference to a minimum at the outer circumference. 2. Equations are derived for the radial pressure (px) and hoop stress (σx) at any point in a thick cylindrical shell subjected to internal fluid pressure. These equations, known as Lame's equations, define px and σx as functions of radius x. 3. An alternate method for finding stresses in a thick cylinder is presented, where circumferential, longitudinal, and radial strains are related to stresses and Poisson's ratio.
Recommended
More Related Content
Similar to Lecture 37 som 07.05.2021
Similar to Lecture 37 som 07.05.2021 (20)
More from BIBIN CHIDAMBARANATHAN
More from BIBIN CHIDAMBARANATHAN (20)
Recently uploaded
Recently uploaded (20)
Lecture 37 som 07.05.2021
- 1. BIBIN CHIDAMBARANATHAN THICK CYLINDER 1 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 2. 2 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 3. Thick cylinders • If the ratio of thickness to internal diameter of a cylindrical shell is less than about 1/20, the cylindrical shell is known as thin cylinders. • The hoop and longitudinal stresses are constant over the thickness and the radial stress is small and can be neglected. • If the ratio of thickness to internal diameter is more than 1/20, then cylindrical shell is known as thick cylinders. • The hoop stress in case of a thick cylinder will not be uniform across the thickness. • Actually, the hoop stress will vary from a maximum value at the inner circumference to a minimum value at the outer circumference. 3 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 4. STRESSES IN A THICK CYLINDRICAL SHELL Fig. shows a thick cylinder subjected to an internal fluid pressure. 4 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 5. Let 𝑟2 = External radius of the cylinder, 𝑟1 = Internal radius of the cylinder, and 𝐿 = Length of cylinder. Consider an elementary ring of the cylinder of radius 𝑥 and thickness 𝑑𝑥 as shown in Fig 5 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 6. Let 𝑝𝑥 = Radial pressure on the inner surface of the ring 𝑝𝑥 + 𝑑𝑝𝑥 = Radial pressure on the outer surface of the ring 𝜎𝑥 = Hoop stress induced in the ring. Take a longitudinal section 𝑥 − 𝑥 and consider the equilibrium of half of the ring of Fig. 6 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
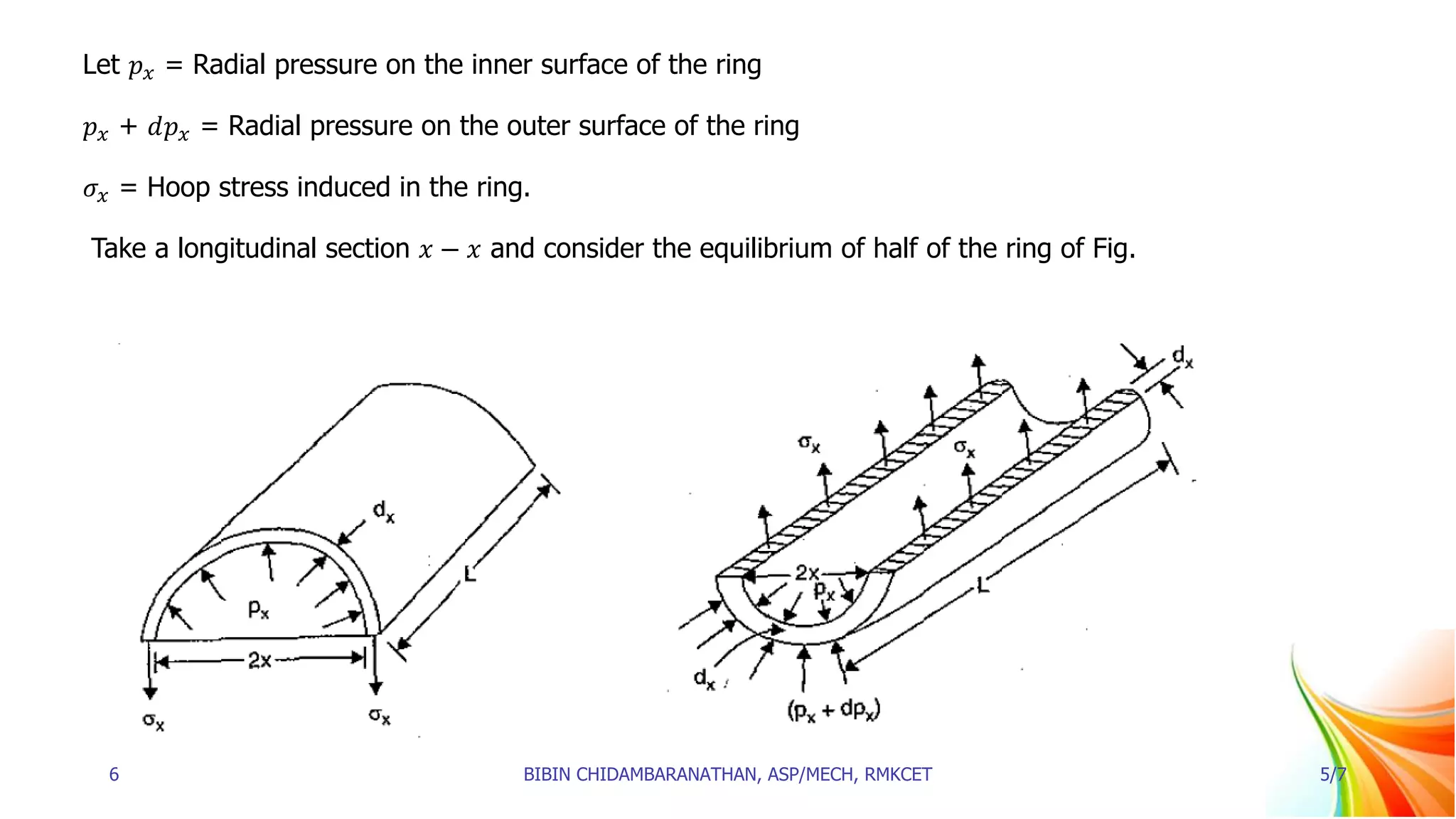
- 7. 𝐵𝑢𝑟𝑠𝑡𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒 = 𝑝𝑥 (2𝑥𝐿) − (𝑝𝑥 + 𝑑𝑝𝑥) × 2(𝑥 + 𝑑𝑥) . 𝐿 = 2𝐿[𝑝𝑥 . 𝑥 − (𝑝𝑥 . 𝑥 + 𝑝𝑥 . 𝑑𝑥 + 𝑥𝑑𝑝𝑥 + 𝑑𝑝𝑥 − 𝑑𝑥)] . (Neglecting 𝑑𝑝 . 𝑑𝑥 which is a small quantity) = 2𝐿[−𝑝𝑥 𝑑𝑥 − 𝑥𝑑𝑝𝑥] = 2𝐿[𝑝𝑥 𝑑𝑥 + 𝑥𝑑𝑝𝑥] 𝑅𝑒𝑠𝑖𝑠𝑡𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒 = 𝐻𝑜𝑜𝑝 𝑠𝑡𝑟𝑒𝑠𝑠 × 𝐴𝑟𝑒𝑎 𝑜𝑛 𝑤ℎ𝑖𝑐ℎ 𝑖𝑡 𝑎𝑐𝑡𝑠 𝑅𝑒𝑠𝑖𝑠𝑡𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒 = 𝜎𝑥 × 2𝑑𝑥. 𝐿 7 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 8. Equating the resisting force to the bursting force, we get 𝜎𝑥 × 2𝑑𝑥. 𝐿 = 2𝐿[𝑝𝑥 𝑑𝑥 + 𝑥𝑑𝑝𝑥] 𝜎𝑥 = −𝑝𝑥 − 𝑥 𝑑𝑝𝑥 𝑑𝑥 The longitudinal strain at any point in the section is constant and is independent of the radius. This means that cross sections remain plane after straining and this is true for sections, remote from any end fixing. As longitudinal strain is constant, hence longitudinal stress will also be constant. 8 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 9. Let 𝜎𝑥 = 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠 Hence at any point at a distance 𝑥 from the centre, three principal stresses are acting They are: (i) the radial compressive stress, 𝑃𝑥 (ii) the hoop (or circumferential) tensile stress, 𝜎𝑥 (iii) the longitudinal tensile stress 𝜎2 9 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 10. The longitudinal strain (𝑒2) at this point is given by, 𝑒2 = 𝜎2 𝐸 − 𝜇𝜎𝑥 𝐸 + 𝜇 𝑝𝑥 𝐸 But longitudinal strain is constant. 𝜎2 𝐸 − 𝜇𝜎𝑥 𝐸 + 𝜇 𝑝𝑥 𝐸 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 But 𝜎2 is also constant, and for the material of the cylinder 𝐸 and μ are constant. 𝜎𝑥 − 𝑃𝑥 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝜎𝑥 − 𝑃𝑥 = 2𝑎 10 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 11. where a is constant 𝜎𝑥 = 𝑃𝑥 + 2𝑎 Equating the two values of 𝜎𝑥 given by equations (iii) and (iv), we get 𝑃𝑥 + 2𝑎 = −𝑝𝑥 − 𝑥 𝑑𝑝𝑥 𝑑𝑥 𝑥 𝑑𝑝𝑥 𝑑𝑥 = −𝑝𝑥 − 𝑝𝑥 − 2𝑎 𝑥 𝑑𝑝𝑥 𝑑𝑥 = −𝑝𝑥 − 𝑝𝑥 − 2𝑎 11 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 12. 𝑥 𝑑𝑝𝑥 𝑑𝑥 = −2𝑝𝑥 − 2𝑎 𝑑𝑝𝑥 𝑑𝑥 = − 2𝑝𝑥 𝑥 − 2𝑎 𝑥 𝑑𝑝𝑥 𝑑𝑥 = − 2(𝑝𝑥 + 𝑎) 𝑥 𝑑𝑝𝑥 (𝑝𝑥+𝑎) = − 2𝑑𝑥 𝑥 12 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 13. Integrating the above equation, we get log𝑒(𝑝𝑥 + 𝑎) = − 2 log𝑒 𝑥 + log𝑒 𝑏 Where log𝑒 𝑏 is a constant of integration The above equation can also be written as log𝑒(𝑝𝑥 + 𝑎) = − log𝑒 𝑥2 + log𝑒 𝑏 log𝑒(𝑝𝑥 + 𝑎) = − log𝑒 𝑏 𝑥2 13 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 14. 𝑝𝑥 + 𝑎 = 𝑏 𝑥2 𝑝𝑥 = 𝑏 𝑥2 − 𝑎 This equation gives the radial pressure 𝑝𝑥 Substituting the values of 𝑃𝑥 in equation (iv), we get 𝜎𝑥 = 𝑏 𝑥2 − 𝑎 + 2𝑎 𝜎𝑥 = 𝑏 𝑥2 + 𝑎 14 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 15. This equation gives the hoop stress at any radius x. These two equations are called Lame's equations. The constants 'a' and 'b' are obtained from boundary conditions, which are: (i) at 𝑥 = 𝑟1, 𝑝𝑥 = 𝑝0 or the pressure of fluid inside the cylinder and (ii) at 𝑥 = 𝑟2, 𝑝𝑥 = 0 or atmosphere pressure. After knowing the values of 'a' and 'b', the hoop stress can be calculated at any radius. 15 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 16. Alternate Method for finding stresses in a thick- cylinder In case of thick cylinders, due to internal fluid pressure, the three principal stresses acting at a point are: (i) radial pressure (p) which is compressive, (ii) circumferential stress or hoop stress (𝜎1) which is tensile, and (iii) longitudinal stress (𝜎2), which is also tensile. Let 𝑒1 = 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑡𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛, 𝑒2 = 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛, 𝑎𝑛𝑑 𝑒𝑟 = 𝑟𝑎𝑑𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 16 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 17. In case of thick-cylinder, it may be assumed that longitudinal strain (𝑒2) is constant, which means that cross-section remain plane after straining. Consider a circular ring of radius rand thickness '𝑑𝑟'. Due to internal fluid pressure, let the radius r increases to (𝑟 + 𝑢) and increase in the thickness 𝑑𝑟 be 𝑑𝑢. Initial radius = r whereas final radius = (r + u) 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑡𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹𝑖𝑛𝑎𝑙 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 − 𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒 17 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 18. 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑡𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 = 2𝜋(𝑟 + 𝑢) − 2𝜋𝑟 2𝜋𝑟 𝑒1 = 2𝜋𝑢 2𝜋𝑟 = 𝑢 𝑟 𝑒1 = 𝑢 𝑟 𝑁𝑜𝑤 𝑜𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑡ℎ𝑖𝑐𝑘𝑛𝑒𝑠𝑠 𝑜𝑓 𝑟𝑖𝑛𝑔 = 𝑑𝑟 𝐹𝑖𝑛𝑎𝑙 𝑡ℎ𝑖𝑐𝑘𝑛𝑒𝑠𝑠 𝑜𝑓 𝑟𝑖𝑛𝑔 = 𝑑𝑟 + 𝑑𝑢 18 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 19. 𝑅𝑎𝑑𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝐹𝑖𝑛𝑎𝑙 𝑡ℎ𝑖𝑐𝑘𝑛𝑒𝑠𝑠 𝑜𝑓 𝑟𝑖𝑛𝑔 − 𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑡ℎ𝑖𝑐𝑘𝑛𝑒𝑠𝑠 𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑡ℎ𝑖𝑐𝑘𝑛𝑒𝑠𝑠 𝑅𝑎𝑑𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 = (𝑑𝑟 + 𝑑𝑢) − 𝑑𝑟 𝑑𝑟 𝑅𝑎𝑑𝑖𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛 = 𝑑𝑢 𝑑𝑟 𝑒𝑟 = 𝑑𝑢 𝑑𝑟 19 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 20. The circumferential strain, longitudinal strain and radial strains in terms of stresses and Poisson's ratio are also given by, 𝑒1 = 𝜎1 𝐸 − 𝜇𝜎2 𝐸 − −𝜇 𝑝 𝐸 (P is compressive) 𝑒1 = 𝜎1 𝐸 − 𝜇𝜎2 𝐸 + 𝜇 𝑝 𝐸 20 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 21. 𝑒2 = 𝜎2 𝐸 − 𝜇𝜎1 𝐸 + 𝜇 𝑝 𝐸 𝑒𝑟 = −𝑝 𝐸 − 𝜇𝜎1 𝐸 + 𝜇𝜎2 𝐸 Equating the two values of circumferential strain (𝑒1) given by equations (i) and (iii). Also equate the two values of radial strain (𝑒𝑟) given by equations (ii) and (v), we get 𝑢 𝑟 = 𝜎1 𝐸 − 𝜇𝜎2 𝐸 + 𝜇 𝑝 𝐸 21 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 22. 𝑑𝑢 𝑑𝑟 = −𝑝 𝐸 − 𝜇𝜎1 𝐸 + 𝜇𝜎2 𝐸 Let us first eliminate 'u' from equations (vi) and (vii). From equation (vi), 𝑢 = [ 𝜎1 𝐸 − 𝜇𝜎2 𝐸 + 𝜇 𝑝 𝐸 ] × 𝑟 Differentiating the above equation with respect to r, we get 𝑑𝑢 𝑑𝑟 = 𝜎1 𝐸 − 𝜇𝜎2 𝐸 + 𝜇 𝑝 𝐸 + 𝑟 𝐸 ( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) 22 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 23. (𝜎1, 𝜎2 and 𝑝 are function of r) 𝐸𝑞𝑢𝑎𝑡𝑖𝑛𝑔 𝑡ℎ𝑒 𝑡𝑤𝑜 𝑣𝑎𝑙𝑢𝑒𝑠 𝑜𝑓 𝑑𝑢 𝑑𝑟 𝑔𝑖𝑣𝑒𝑛 𝑏𝑦 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠 (𝑣𝑖𝑖) 𝑎𝑛𝑑 (𝑣𝑖𝑖𝑖), −𝑝 𝐸 − 𝜇𝜎1 𝐸 + 𝜇𝜎2 𝐸 = 𝜎1 𝐸 − 𝜇𝜎2 𝐸 + 𝜇 𝑝 𝐸 + 𝑟 𝐸 ( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) −𝑝 − 𝜇𝜎1 + 𝜇𝜎2 = 𝜎1 − 𝜇𝜎2 + 𝜇𝑝 + 𝑟( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) 23 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 24. (Cancelling E to both sides) 0 = 𝑝 + 𝜇𝜎1 + 𝜇𝜎2 +𝜎1 −𝜇𝜎2 + 𝜇𝑝 + 𝑟( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) 0 = 𝑝(1 + 𝜇) + 𝜎1(1 + 𝜇) + 𝑟( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) 24 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 25. To find the value of 𝜎1 in terms of p, the value of 𝑑𝜎2 𝑑𝑟 must be substituted in the above equation (ix). Longitudinal strain (𝑒2) is given by equation (iv) as 𝑒2 = 𝜎2 𝐸 − 𝜇𝜎1 𝐸 + 𝜇 𝑝 𝐸 Since longitudinal strain (𝑒2) is assumed constant. Its differentiation with respect to r will be zero. D1fferentiating the above equation with respect to 'r', we get 0 = 1 𝐸 [ 𝑑𝜎2 𝑑𝑟 − 𝜇𝑑𝜎1 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ] 25 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 26. 0 = 𝑑𝜎2 𝑑𝑟 − 𝜇𝑑𝜎1 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 𝑑𝜎2 𝑑𝑟 = 𝜇𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝑝 𝑑𝑟 Substituting the value of 𝑑𝜎2 𝑑𝑟 in equation (ix), we get 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟( 𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝜎2 𝑑𝑟 + 𝜇 𝑑𝑝 𝑑𝑟 ) 26 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 27. 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟( 𝑑𝜎1 𝑑𝑟 − 𝜇( 𝜇𝑑𝜎1 𝑑𝑟 − 𝜇 𝑑𝑝 𝑑𝑟 ) + 𝜇 𝑑𝑝 𝑑𝑟 ) 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟( 𝑑𝜎1 𝑑𝑟 (1 − 𝜇2 ) + 𝜇 𝑑𝑝 𝑑𝑟 (1 + 𝜇) 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟(1 − 𝜇2 ) 𝑑𝜎1 𝑑𝑟 + 𝜇𝑟(1 + 𝜇) 𝑑𝑝 𝑑𝑟 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟(1 + 𝜇)(1 − 𝜇) 𝑑𝜎1 𝑑𝑟 + 𝜇𝑟(1 + 𝜇) 𝑑𝑝 𝑑𝑟 27 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 28. 0 = (𝑝 + 𝜎1)(1 + 𝜇) + 𝑟(1 + 𝜇)(1 − 𝜇) 𝑑𝜎1 𝑑𝑟 + 𝜇𝑟(1 + 𝜇) 𝑑𝑝 𝑑𝑟 0 = 1 + 𝜇 [(𝑝 + 𝜎1) + 𝑟(1 − 𝜇) 𝑑𝜎1 𝑑𝑟 + 𝜇𝑟 𝑑𝑝 𝑑𝑟 ] (1 + 𝜇) ≠ 0 0 = (𝑝 + 𝜎1) + 𝑟(1 − 𝜇) 𝑑𝜎1 𝑑𝑟 + 𝜇𝑟 𝑑𝑝 𝑑𝑟 28 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 29. For the equilibrium of the element, resolving the forces acting on the element in the radial direction we get 0 = 𝑝 + 𝑑𝑝 𝑟 + 𝑑𝑟 𝛿𝜃 + 2𝜎1 × 𝑑𝑟 × 𝑠𝑖𝑛 𝛿𝜃 2 As 𝛿𝜃 is small, hence 𝑠𝑖𝑛 𝛿𝜃 2 = 𝛿𝜃 2 Now the above equation becomes 0 = 𝑝 + 𝑑𝑝 𝑟 + 𝑑𝑟 𝛿𝜃 + 2𝜎1 × 𝑑𝑟 × 𝑠𝑖𝑛 𝛿𝜃 2 29 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 30. 30 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
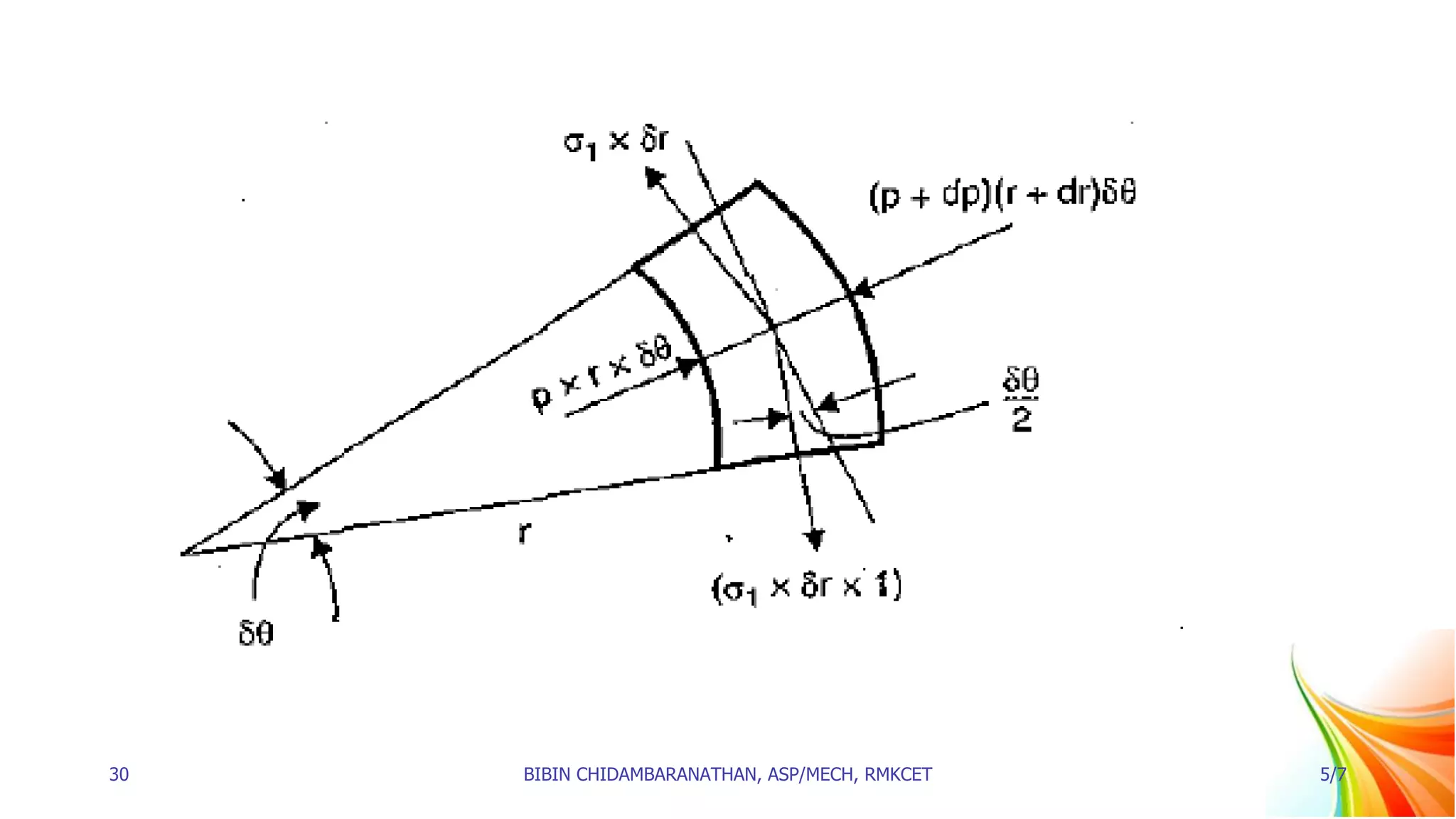
- 31. 𝑝 + 𝑑𝑝 𝑟 + 𝑑𝑟 𝛿𝜃 + 𝑝𝑟𝛿𝜃 + 2𝜎1 × 𝑑𝑟 × 𝛿𝜃 2 = 0 𝑝 + 𝑑𝑝 𝑟 + 𝑑𝑟 − 𝑝𝑟 + 𝜎1 × 𝑑𝑟 = 0 𝑝𝑟 + 𝑝𝑑𝑟 + 𝑟𝑑𝑝 + 𝑑𝑝 × 𝑑𝑟 − 𝑝𝑟 + 𝜎1 × 𝑑𝑟 = 0 𝑝𝑑𝑟 + 𝑟𝑑𝑝 + 𝜎1𝑑𝑟 = 0 [dp x dr is the product of two small quantities and can be neglected] 31 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 32. 𝑝 + 𝑟 𝑑𝑝 𝑑𝑟 + 𝜎1 = 0 𝑝 + 𝜎1 = −𝑟 𝑑𝑝 𝑑𝑟 Substituting the value of 𝑝 + 𝜎1 in equation (𝑥), we get 0 = (𝑝 + 𝜎1) + 𝑟(1 − 𝜇) 𝑑𝜎1 𝑑𝑟 + 𝜇𝑟 𝑑𝑝 𝑑𝑟 0 = −𝑟 𝑑𝑝 𝑑𝑟 1 − 𝜇 + 𝑟(1 − 𝜇) 𝑑𝜎1 𝑑𝑟 [Cancelling 𝑟(1 – 𝜇) to both sides] 32 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 33. 0 = − 𝑑𝑝 𝑑𝑟 + 𝑑𝜎1 𝑑𝑟 − 𝑑𝑝 𝑑𝑟 + 𝑑𝜎1 𝑑𝑟 = 0 Integrating, we get 𝜎1 − 𝑝 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝜎1 − 𝑝 = 2𝑎 33 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 34. In equations (xii) and (xi), the two unknowns are 𝜎1 and 𝑝. Let us find the value of 𝜎1 from equation (xii) and substitute this value in equation (xi). 𝑝 + (2𝑎 + 𝑝) = −𝑟 𝑑𝑝 𝑑𝑟 2𝑎 + 2𝑝 = −𝑟 𝑑𝑝 𝑑𝑟 2𝑝 + 𝑟 𝑑𝑝 𝑑𝑟 = −2𝑎 34 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 35. 1 𝑟 × 𝑑(𝑝𝑟2 ) 𝑑𝑟 = −2𝑎 𝑑(𝑝𝑟2 ) 𝑑𝑟 = −2𝑎𝑟 Integrating, we get 𝑝𝑟2 = −2𝑎𝑟2 2 + 𝑏 where b is another constant. 35 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 36. 𝑝𝑟2 = 𝑎𝑟2 + 𝑏 𝑝 = −𝑎𝑟2 𝑟2 + 𝑏 𝑟2 𝑝 = 𝑏 𝑟2 − 𝑎 The above equation gives the radial pressure at radius 'r'. This equation is same as equation. To find the value of 𝜎1 at any radius, substitute this value of p in equation (xiii). 36 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 37. 𝜎1 − 𝑏 𝑟2 − 𝑎 = 2𝑎 𝜎1 − 𝑏 𝑟2 + 𝑎 = 2𝑎 𝜎1 = 𝑏 𝑟2 + 2𝑎 − 𝑎 𝜎1 = 𝑏 𝑟2 + 𝑎 The above equation gives the circumferential stress (or hoop stress) at any radius r. This equation is same as equation 37 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 38. 38 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 39. 39 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 40. 40 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 41. Problem 1. Determine the maximum and minimum hoop stress across the section of a pipe of 400 mm internal diameter and 100 mm thick, when the pipe contains a fluid at a pressure of 8 𝑁/𝑚𝑚2 . Also sketch the radial pressure distribution and hoop stress distribution across the section. Internal dia. = 400 mm Internal radius = 200 mm Thickness = 100 mm External dia. = 600 mm External radius = 300 mm 41 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 42. Fluid pressure, p = 8 𝑁/𝑚𝑚2 The radial pressure (px) is given by equation 𝑝𝑥 = 𝑏 𝑟2 − 𝑎 Now apply the boundary conditions to the above equations. The boundary conditions (i) at 𝑥 = 𝑟1, 𝑝𝑥 = 𝑝0 or the pressure of fluid inside the cylinder and (ii) at 𝑥 = 𝑟2, 𝑝𝑥 = 0 or atmosphere pressure. Substituting these boundary conditions in equation (i), we get 42 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 43. 8 = 𝑏 2002 − 𝑎 0 = 𝑏 3002 − 𝑎 8 = 𝑏 40000 − 𝑎 0 = 𝑏 90000 − 𝑎 Subtracting equation (iii) from equation (ii), we get 43 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 44. 8 = 𝑏 40000 − 𝑎 − 𝑏 90000 + 𝑎 8 = 𝑏 40000 − 𝑏 90000 8 = 9𝑏 − 4𝑏 360000 8 = 5𝑏 360000 44 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 45. 8 = 5𝑏 360000 𝑏 = 36000 × 8 5 𝑏 = 576000 Substituting this value in equation (iii), we get 0 = 576000 90000 − 𝑎 45 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 46. 𝑎 = 576000 90000 𝑎 = 6.4 The values of 'a' and 'b' are substituted in the hoop stress. 𝜎𝑥 = 𝑏 𝑥2 + 𝑎 𝜎𝑥 = 576000 𝑥2 + 6.4 46 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 47. 𝑥 = 200𝑚𝑚 𝜎200 = 576000 2002 + 6.4 𝜎200 = 14.4 + 6.4 𝜎200 = 20.8 𝑁 𝑚𝑚2 𝑥 = 300𝑚𝑚 47 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 48. 𝜎300 = 576000 3002 + 6.4 𝜎300 = 6.4 + 6.4 𝜎300 = 12.8 𝑁/𝑚𝑚2 Fig. 18.3 shows the radial pressure distribution and hoop stress distribution across the section. AB is taken a horizontal line. AC= 8 𝑁/𝑚𝑚2 . The variation between B and C is parabolic. The curve BC shows the variation of radial pressure across AB. 48 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 49. The curve DE which is also parabolic, shows the variation of hoop stress across AB. Values BD = 12.8 𝑁/𝑚𝑚2 and AE = 20.8 𝑁/𝑚𝑚2 . The radial pressure is compressive whereas the hoop stress is tensile. 49 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 50. Problem 2. Find the thickness of metal necessary for a cylindrical shell of internal diameter 160 mm to withstand an internal pressure of 8 𝑁/𝑚𝑚2 . The maximum hoop stress in the section is not to exceed 35 𝑁/𝑚𝑚2 . Internal dia. = 160 mm Internal radius =80 mm Internal pressure = 8 𝑁/𝑚𝑚2 This means at x = 80 mm, 𝑝𝑥 = 8 𝑁/𝑚𝑚2 50 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 51. Maximum hoop stress 𝜎𝑥 = 35 𝑁/𝑚𝑚2 The maximum hoop stress is at the inner radius of the shell. Let 𝑟2 = External radius. The radial pressure and hoop stress at any radius 𝑥 are given by equations 𝑝𝑥 = 𝑏 𝑟2 − 𝑎 𝜎𝑥 = 𝑏 𝑥2 + 𝑎 51 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 52. Now apply the boundary conditions to the above equations. The boundary conditions (i) at 𝑥 = 𝑟1, 𝑝𝑥 = 𝑝0 or the pressure of fluid inside the cylinder and (ii) at 𝑥 = 𝑟2, 𝑝𝑥 = 0 or atmosphere pressure. Substituting these boundary conditions in equation (i), we get 8 = 𝑏 802 − 𝑎 8 = 𝑏 6400 − 𝑎 52 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 53. Subtracting equation (iii) from equation (ii), we get 35 = 𝑏 802 + 𝑎 35 = 𝑏 6400 + 𝑎 Subtracting equation (iii) from equation (iv), we get 27 = 2𝑎 𝑎 = 13.5 53 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 54. Substituting the value of a in equation (iii), we get 8 = 𝑏 6400 − 13.5 𝑏 = 21.5 × 6400 Substituting the values of 'a' and 'b' in equation (i), 𝑝𝑥 = 21.5 × 6400 𝑥2 − 13.5 54 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 55. But at the outer surface, the pressure is zero. Hence at 𝑥 = 𝑟2, 𝑃𝑥 = 0. Substituting these values in the above equation, we get 0 = 21.5 × 6400 𝑟1 2 − 13.5 𝑟2 2 = 21.5 × 6400 13.5 𝑟2 = 21.5 × 6400 13.5 55 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 56. 𝑟2 = 100.96 𝑚𝑚 Thickness of the shell, 𝑡 = 𝑟2 − 𝑟1 𝑡 = 100.96 – 80 𝑡 = 20.96 𝑚𝑚 56 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 57. 57 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 58. 58 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 59. 59 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 60. 60 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 61. 61 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 62. 62 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 63. 63 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 64. 64 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 65. 65 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 66. 66 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 67. BIBIN CHIDAMBARANATHAN COMPOUND CYLINDER 67 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 68. 68 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 69. 69 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 70. 70 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 71. 71 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 72. 72 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 73. 73 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 74. 74 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 75. 75 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 76. 76 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 77. 77 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 78. 78 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 79. 79 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 80. 80 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 81. 81 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7
- 82. Thank You 82 BIBIN CHIDAMBARANATHAN, ASP/MECH, RMKCET 5/7