This document provides an overview of periodic signals in continuous and discrete time. It discusses the key properties of periodic signals including fundamental period and frequency. Periodic signals can be even, odd, exponential, or sinusoidal. Complex exponential signals are introduced and their relationship to sinusoidal signals via Euler's formula is explained. Harmonically related signals are periodic signals whose frequencies are integer multiples of a fundamental frequency. More general complex exponential signals are expressed as a product of a sinusoid and a growing, decaying, or constant exponential term.

1. EC2610:Fundamentals of Signals and Systems
By
Sadananda Behera
Assistant Professor
Department of Electronics and Communication Engineering
NIT, Rourkela
1
CHAPTER-1 : SIGNALS AND SYSTEMS-Part 2

2. Periodic Signals
Continuous-Time Signals
• A continuous time signal 𝑥(𝑡) is said to be periodic if, for positive value of 𝑇, the
following condition hold.
𝑥(𝑡) = 𝑥(𝑡 + 𝑇) for all t.
• A periodic signal has the property that it is unchanged by a time shift of T
• If a signal is periodic with 𝑇, then 𝑥(𝑡) = 𝑥(𝑡 + 𝑚𝑇) where m is an integer. So 𝑥(𝑡)
is also periodic with 2𝑇, 3𝑇. .
• The fundamental period 𝑇0 of 𝑥(𝑡) is the smallest positive value of 𝑇 for which
𝑥(𝑡) = 𝑥(𝑡 + 𝑇) holds
• If 𝑥(𝑡) is constant, then fundamental period is undefined since 𝑥(𝑡) is periodic for
any choice of 𝑇 .
• A signal that is not periodic is called aperiodic signal.
2

3. Continuous-time Periodic Signal
3

4. t
𝑥(𝑡)
𝑥(𝑡) = 4
0
4
Continuous-time Periodic Signal
4
𝑥(𝑡) = 𝑥(𝑡 + 𝑇) for all t
The fundamental period is undefined

5. Discrete-Time Signals
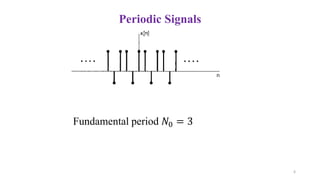
• A discrete-time signal (sequence) 𝑥[𝑛] is said to be periodic with period 𝑁, where
𝑁 is a positive integer, if the following condition hold .
𝑥[𝑛] = 𝑥[𝑛 + 𝑁] for all 𝑛
• 𝑥[𝑛] is also periodic with 2𝑁, 3𝑁. .
• The fundamental period 𝑁0 is the smallest positive value of 𝑁 for which
𝑥[𝑛] = 𝑥[𝑛 + 𝑁] holds
Periodic Signals
5

6. Fundamental period 𝑁0 = 3
Periodic Signals
6

7. Even and Odd Signals
A signal 𝑥(𝑡) or 𝑥[𝑛] is refer to as even signal if it is identical to its time-reversed
counterpart, i.e.,
• 𝑥(−𝑡) = 𝑥(𝑡) [Continuous-time]
• 𝑥[−𝑛] = 𝑥[𝑛] [Discrete-time]
A signal is referred to as odd if
• 𝑥 −𝑡 = −𝑥(𝑡) [Continuous-time]
• 𝑥 −𝑛 = −𝑥[𝑛] [Discrete-time]
An odd signal must necessarily be 0 at 𝑡 = 0 or 𝑛 = 0
• 𝑥(0) = −𝑥(0) ⇒ 𝑥 0 = 0
• 𝑥[0] = −𝑥[0] ⇒ 𝑥[0] = 0
7

8. Even and Odd Signals
8
Even Odd
𝑥[𝑛] 𝑥[𝑛]

9. • Every Signal can be broken into a sum of two signals one of which is even and the
other is odd.
𝑥(𝑡)=
1
2
[𝑥 𝑡 + 𝑥 −𝑡 + 𝑥 𝑡 − 𝑥(−𝑡)]=
1
2
[𝑥 𝑡 + 𝑥(−𝑡)] +
1
2
[𝑥 𝑡 − 𝑥(−𝑡)]
Even
Odd
Even and Odd Signals
9

10. • Continuous-Time
• Ev[𝑥(𝑡)]=
1
2
[𝑥 𝑡 + 𝑥(−𝑡)] [Even Function]
• Od[𝑥(𝑡)]=
1
2
[𝑥 𝑡 − 𝑥(−𝑡)] [Odd Function]
• Discrete-Time
• Ev[𝑥[𝑛]]=
1
2
[𝑥[𝑛] + 𝑥[−𝑛]]
• Od[𝑥[𝑛]]=
1
2
[𝑥[𝑛] − 𝑥[−𝑛]]
Even and Odd Signals
10

11. Exponential and Sinusoidal Signals
Continuous-time Complex Exponential and Sinusoidal signals
• The continuous-time complex exponential signal is of the form 𝑥(𝑡) = 𝐶𝑒𝑎𝑡
where 𝐶
and 𝑎 are complex numbers
• The complex exponential can exhibit different characteristics depending upon its
parameter 𝐶 and 𝑎.
Real-Exponential signals
• A real exponential is a special case of complex exponential 𝑥(𝑡) = 𝐶𝑒𝑎𝑡 where 𝐶 and 𝑎
are restricted to be real numbers
a) If 𝑎 > 0, 𝑥(𝑡) increases exponentially as t increases (Growing exponential)
b) If 𝑎 < 0, 𝑥(𝑡) decreases exponentially as t increases (Decaying exponential)
c) If 𝑎 = 0, 𝑥(𝑡) is a constant.
11

12. Real Exponential signals
Exponential Increasing(𝑎 > 0)
Exponential Decreasing(𝑎 < 0)
t
𝑥(𝑡)
0
C
Constant Signal (𝑎 = 0)
12
(𝑐)
𝑥(𝑡) = 𝐶𝑒𝑎𝑡

13. Periodic Complex Exponential and Sinusoidal Signals
Complex Exponentials
• a is purely imaginary
• A continuous-time complex exponential can be represented as 𝑥 𝑡 = 𝑒𝑗𝜔0𝑡
• If it is a periodic signal, then 𝑒𝑗𝜔0𝑡 = 𝑒𝑗𝜔0(𝑡+𝑇) = 𝑒𝑗𝜔0𝑡. 𝑒𝑗𝜔0𝑇 ⇒ 𝑒𝑗𝜔0𝑇 = 1
• If 𝜔0=0 then 𝑥(𝑡) = 1(constant), which is periodic with any value of 𝑇
• If 𝜔0≠0 then the fundamental period 𝑇0 (Smallest value of 𝑇 for which 𝑒𝑗𝜔0𝑇 = 1) of
𝑥(𝑡) is
𝑇0 =
2𝜋
𝜔0
… … … … … … … … … … … … … … … . (1)
• The signals 𝑒𝑗𝜔0𝑡
and 𝑒−𝑗𝜔0𝑡
have the same fundamental period.
13

14.  Sinusoidal Signals
• A sinusoidal signal can be represented as 𝑥(𝑡) = A cos(𝜔0𝑡 + 𝜑 )
t→seconds
𝜔0 →radians/second
𝜑 →radians
𝜔0= 2𝜋𝑓0 where 𝑓0 is in cycles/second or Hz
• The sinusoidal signal is periodic
with fundamental period 𝑇0 =
2𝜋
𝜔0
Periodic Complex Exponential and Sinusoidal Signals
14

15. • 𝑒𝑗𝜔0𝑡=cos 𝜔0𝑡 + 𝑗sin 𝜔0𝑡
• 𝐴𝑐𝑜𝑠(𝜔0𝑡 + 𝜑)=
𝐴
2
𝑒𝑗(𝜔0𝑡+𝜑)+
𝐴
2
𝑒−𝑗(𝜔0𝑡+𝜑)=
𝐴
2
𝑒𝑗𝜑𝑒𝑗𝜔0𝑡+
𝐴
2
𝑒−𝑗𝜑𝑒−𝑗𝜔0𝑡
• A cos(𝜔0𝑡 + 𝜑)=A Re{ 𝑒𝑗(𝜔0𝑡+𝜑) }
• A sin(𝜔0𝑡 + 𝜑)=A Im{ 𝑒𝑗(𝜔0𝑡+𝜑)}
Periodic Complex Exponential and Sinusoidal Signals
15
Euler’s relation establishes the fundamental relationship between the
trigonometric functions and the complex exponential functions.

16. From (1) it is clear that the fundamental period 𝑇0 of a continuous-time signal or a
periodic complex exponential is inversely proportional to 𝜔0, which is named as
fundamental frequency
• If the magnitude of 𝜔0 decreases ( rate of oscillation decreases) then the
fundamental period increases and vice-versa.
• If 𝑥(𝑡) is a constant signal then it is periodic with any positive value of 𝑇. Thus
the fundamental period of a constant signal is undefined.
• The fundamental frequency of a constant signal to be zero i.e. a constant signal
has zero rate of oscillation
Periodic Complex Exponential and Sinusoidal Signals
16

17. 𝜔1 > 𝜔2 > 𝜔3
⇒ 𝑇1 < 𝑇2 < 𝑇3
Periodic Complex Exponential and Sinusoidal Signals
17

18. • Total energy over one period
𝐸𝑝𝑒𝑟𝑖𝑜𝑑= |𝑒𝑗𝜔𝑡|2𝑑𝑡
𝑇0
0
= 1𝑑𝑡
𝑇0
0
= 𝑇0
• Average Power over one period
𝑃𝑝𝑒𝑟𝑖𝑜𝑑 =
1
𝑇0
𝐸𝑝𝑒𝑟𝑖𝑜𝑑 = 1
• Since there are infinite number of periods as 𝑡 ranges from −∞ to ∞ the total energy
integrated over all time is infinite. So 𝐸∞ = ∞
Since the average power of the signal equals 1 over each period, averaging over multiple
periods will always yields an average power of 1
Average Power
𝑃∞ ≜ lim
𝑇→∞
1
2𝑇
𝑒𝑗𝜔𝑡 2
𝑑𝑡
𝑇
−𝑇
= 1
Periodic Complex Exponential and Sinusoidal Signals
18

19. These are sets of periodic exponentials, all of which are periodic with a common period
𝑇0. If 𝑒𝑗𝜔𝑡
is periodic with 𝑇0, then
𝑒𝑗𝜔(𝑡+𝑇0)= 𝑒𝑗𝜔𝑡
⇒ 𝑒𝑗𝜔𝑇0= 1 ⇒ 𝜔𝑇0 = 2𝜋𝑘……..(2),
𝑘 = 0, ±1, ±2, ±3, …
Define 𝜔0=
2𝜋
𝑇0
………………………...…(3)
From eq (2) and eq (3)
ω = 𝑘𝜔0
𝜔 must be an integer multiple of 𝜔0
Harmonically related complex exponentials
19

20. A harmonically related set of complex exponentials is a set of periodic
exponentials with fundamental frequency that are all multiples of single positive
frequency 𝜔0:
𝜑𝑘 = 𝑒𝑗𝑘𝜔0𝑡, 𝑘 = 0, ±1, ±2, ±3, …
𝑘 = 0, 𝜑𝑘(𝑡) is a constant
For any other value of 𝑘, 𝜑𝑘(𝑡) is periodic with fundamental frequency 𝑘 𝜔0 and
fundamental period is
2𝜋
𝑘 𝜔0
=
𝑇0
𝑘
The 𝑘𝑡ℎ harmonic 𝜑𝑘(𝑡) is still periodic with period 𝑇0 as well, as it goes through
exactly 𝑘 number of its fundamental periods during any intervals of length 𝑇0
Harmonically related complex exponentials
20

21. 𝑇0, 𝜔0
𝑇0/2, 2𝜔0
Also periodic with 𝑇0
𝑇0/3, 3𝜔0 Also periodic with 𝑇0
Harmonically related complex exponentials
21

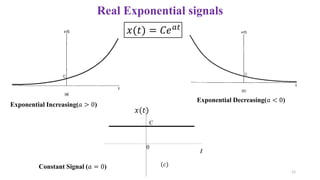
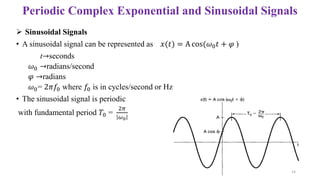
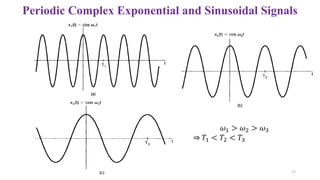
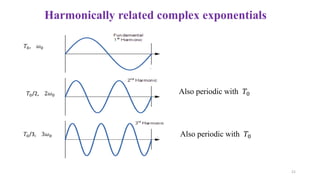
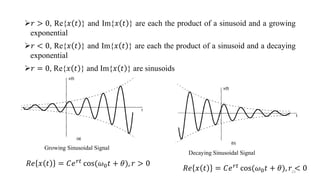
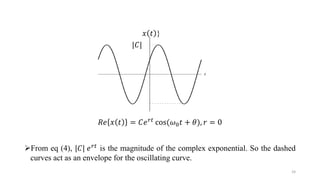
22. General Complex Exponentials
𝑥(𝑡) = 𝐶𝑒𝑎𝑡, 𝐶 and 𝑎 both are complex
• 𝐶 = |𝐶|𝑒𝑗𝜃 [Polar form]
• 𝑎 = 𝑟 + 𝑗𝜔0 [Rectangular form]
𝐶𝑒𝑎𝑡 = |𝐶|𝑒𝑗𝜃 𝑒(𝑟+𝑗𝜔0)𝑡 = |𝐶|𝑒𝑟𝑡𝑒𝑗(𝜔0𝑡+𝜃) ……...(4)
𝑥(𝑡) = 𝐶𝑒𝑎𝑡
= |𝐶|𝑒𝑟𝑡
cos(𝜔0𝑡 + 𝜃) + 𝑗 |𝐶|𝑒𝑟𝑡
sin(𝜔0𝑡 + 𝜃)
𝑅𝑒 𝑥 𝑡 𝐼𝑚{𝑥(𝑡)}
22

23. 𝑟 > 0, Re{𝑥 𝑡 } and Im{𝑥 𝑡 } are each the product of a sinusoid and a growing
exponential
𝑟 < 0, Re{𝑥 𝑡 } and Im{𝑥 𝑡 } are each the product of a sinusoid and a decaying
exponential
𝑟 = 0, Re{𝑥 𝑡 } and Im{𝑥 𝑡 } are sinusoids
Growing Sinusoidal Signal
Decaying Sinusoidal Signal
𝑅𝑒 𝑥 𝑡 = 𝐶𝑒𝑟𝑡 cos(𝜔0𝑡 + 𝜃), 𝑟 > 0
𝑅𝑒 𝑥 𝑡 = 𝐶𝑒𝑟𝑡 cos(𝜔0𝑡 + 𝜃), 𝑟 < 0
23

24. |𝐶|
From eq (4), |𝐶| 𝑒𝑟𝑡 is the magnitude of the complex exponential. So the dashed
curves act as an envelope for the oscillating curve.
𝑅𝑒 𝑥 𝑡 = 𝐶𝑒𝑟𝑡
cos(𝜔0𝑡 + 𝜃), 𝑟 = 0
|𝐶|
𝑥 𝑡 }
24

25. THANK YOU
25