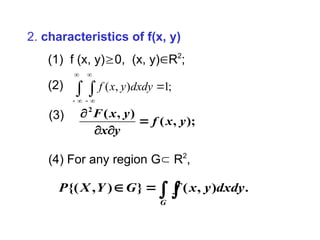The document discusses multivariate random variables, defining them as mathematical vectors where each variable's value is uncertain. It elaborates on joint distributions for n-dimensional random vectors, including characteristics and examples for both continuous and discrete joint distributions. Additionally, it explains the probability computation related to these random variables and their functions.

1. Multivariate Random Variables
Multivariate random variable or Random vector is a list of
mathematical variables each of whose value is unknown,
Either because the value has not yet occurred or
because there is imperfect knowledge of its value.
The individual variables in a random vector are
grouped together because they are all part of a
single mathematical system — often they
represent different properties of an
individual statistical unit

2. 1.n-dimensional variables
n random variables X1 ， X2 ， ...,Xn compose a n-
dimensional vector (X1,X2,...,Xn), and the vector is
named n-dimensional variables or random vector.
2. Joint distribution of random vector
Define function
F(x1,x2,…xn)= P(X1≤x1,X2 ≤ x2,...,Xn ≤ xn)
the joint distribution function of random vector
(X1,X2,...,Xn).
Two-Dimensional Random Variables

3. Definition Let (X, Y) be 2-dimensional random
variables. Define F(x,y) = P{Xx, Yy}
the bivariate cdf of (X, Y) .
The Joint cdf for Two random variables
 
 
0
0 ,
,
, y
y
x
x
y
x 





Geometric interpretation ：
the value of F( x, y) assume
the probability that the random
points belong to area in dark

4. For (x1, y1), (x2, y2)R2
, (x1< x2 ， y1<y2 ), then
P{x1<X x2 ， y1<Yy2 }
＝ F(x2, y2) － F(x1, y2) － F (x2, y1) ＋ F (x1, y1).
(x1, y1)
(x2, y2)
(x2, y1)
(x1, y2)

5. 1
x 2
x 3
x
1
y
2
y
3
y
Suppose that the joint cdf of (X,Y) is F(x,y), find the probability that
(X,Y) stands in area G .
Answer
2 1 3 3 2 3 3 1
1 2 2 3 1 3 2 2
{( , ) } [ ( , ) ( , ) ( , ) ( , )]
[ ( , ) ( , ) ( , ) ( , )]
P X Y G F x y F x y F x y F x y
F x y F x y F x y F x y
    
    L

6. Joint distribution F(x, y) has the following
characteristics:
0
)
,
(
lim
)
,
( 







y
x
F
F
y
x
1
)
,
(
lim
)
,
( 







y
x
F
F
y
x
0
)
,
(
lim
)
,
( 




y
x
F
y
F
x
0
)
,
(
lim
)
,
( 




y
x
F
x
F
y
(1) For all (x, y) R2
, 0 F(x, y)  1,

7. (2) Monotonically increment
for any fixed y R, x1<x2 yields
F(x1, y)  F(x2 , y) ；
for any fixed x R, y1<y2 yields
F(x, y1)  F(x , y2).
);
y
,
x
(
F
)
y
,
x
(
F
lim
)
y
,
0
x
(
F 0
x
x
0
0


 

).
y
,
x
(
F
)
y
,
x
(
F
lim
)
0
y
,
x
(
F 0
y
y
0
0


 

(3) right continuous for xR, yR,

8. (4) for all (x1, y1), (x2, y2)R2
, (x1< x2 ， y1<y2 ),
F(x2, y2) － F(x1, y2) － F (x2, y1) ＋ F (x1, y1)0.
Conversely, any real-valued function satisfied
the aforementioned 4 characteristics must be
a joint distribution function of 2-dimensional
variables.

9. Example 1. Let the joint distribution of (X,Y) is
)]
3
(
)][
2
(
[
)
,
(
y
arctg
C
x
arctg
B
A
y
x
F 


1) Find the value of A ， B ， C 。
2) Find P{0<X<2,0<Y<3}
Answer 1
]
2
][
2
[
)
,
( 







C
B
A
F
0
)]
3
(
][
2
[
)
,
( 




y
arctg
C
B
A
y
F

0
]
2
)][
2
(
[
)
,
( 





C
x
arctg
B
A
x
F
2
1
2 




 A
C
B
16
1
)
0
,
2
(
)
3
,
0
(
)
3
,
2
(
)
0
,
0
(
}
3
0
,
2
0
{ 







 F
F
F
F
Y
X
P

10. Discrete joint distribution
If both x and y are discrete random variable,
then,(X, Y) take values in (xi, yj), (i, j ＝ 1, 2, … ), it is said
that X and Y have a discrete joint distribution .
Definition
The joint distribution is defined to be a function
such that for any points (xi, yj),
P{X ＝ xi, Y ＝ yj,} ＝ pij ， (i, j ＝ 1, 2, … ).
That is
(X, Y) ～ P{X ＝ xi, Y ＝ yj,} ＝ pij ， (i, j ＝ 1, 2, …

11. X
Y y
1
y
2
… y
j
…
p11 p12 ... P1j ...
p21 p22 ... P2j ...
pi1 pi2 ... Pij ...
..
.
...
...
...
...
...
..
.
..
.
Characteristics of joint distribution :
(1) pij 0 , i, j ＝ 1, 2, … ；
(2) 1
1 1
＝
 
 
i j
ij
p
x1
x2
xi
The joint distribution can also be specified in the
following table

12. Example 2. Suppose that there are two red balls and three
white balls in a bag, catch one ball from the bag twice
without put back, and define X and Y as follows:








ball
white
is
put
second
the
0
ball
red
is
put
second
the
1
ball
white
is
put
first
the
0
ball
red
is
put
first
the
1
Y
X
Please find the
joint pmf of (X,Y)
X
Y
1
0
1 0
10
1
10
3
10
3
10
3
2
5
2
2
}
1
,
1
{
P
P
Y
X
P 


2
5
3
2
}
0
,
1
{
P
Y
X
P




2
5
2
3
}
1
,
0
{
P
Y
X
P




2
5
2
3
}
0
,
0
{
P
P
Y
X
P 



13. Continuous joint distributions and
density functions
1. It is said that two random variables (X, Y) have a continuous
joint distribution if there exists a nonnegative function f (x, y)
such that for all (x, y)R2
， the distribution function satisfies


 


x y
dudv
v
u
f
y
x
F ,
)
,
(
)
,
(
and denote it with
(X, Y) ～ f (x, y) ， (x, y)R2

14. 2. characteristics of f(x, y)
(1) f (x, y)0, (x, y)R2
;
(2)
);
,
(
)
,
(
2
y
x
f
y
x
y
x
F




(3)
( , ) 1;
f x y dxdy
 
 


－ －
(4) For any region G R2
,



G
dxdy
y
x
f
G
Y
X
P .
)
,
(
}
)
,
{(

15. 


G
dxdy
y
x
f
G
Y
X
P .
)
,
(
}
)
,
{(
Let


 




others
y
x
y
x
f
Y
X
0
1
0
,
1
0
1
)
,
(
~
)
,
(
Find P{X>Y}
2
1
1
}
{
0
1
0



 

x
dy
dx
Y
X
P
1
1
x
y

16. Find (1)the value of A ；
(2) the value of F(1,1) ；
(3) the probability of (X, Y) stand in
region D ： x0, y0, 2X+3y6


 




cases
other
for
,
0
0
,
0
,
)
,
(
~
)
,
(
)
3
2
(
y
x
Ae
y
x
f
Y
X
y
x
Answer (1) Since
6

 A









1
0
1
0
3
2
)
3
2
(
)
1
)(
1
(
6
)
1
,
1
(
)
2
( e
e
dxdy
e
F y
x
1
1
   
 
  
－ －
-(2x+3y)
0 0
f(x, y)dxdy = Ae dxdy = 1

17. (3)
 




3
0
3
2
2
0
)
3
2
(
6 dy
e
dx
x
y
x
6
7
1 

 e
dxdy
e
D
Y
X
P
D
y
x




 )
3
2
(
6
}
)
,
{(

18. Operations on random vectors