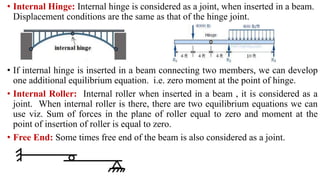
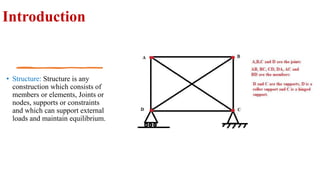
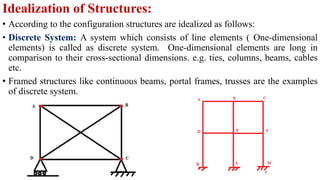
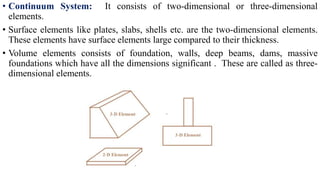
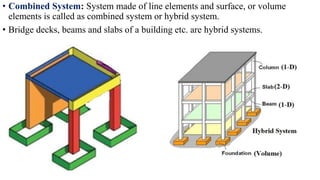
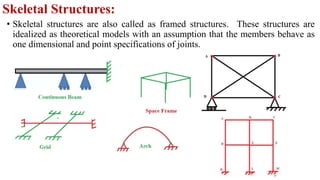
The document discusses different types of structures including discrete systems made of line elements like beams and columns, continuum systems with surface or volume elements like plates and shells, and hybrid systems combining different element types. It also defines structure as any construction consisting of members, joints, supports that can resist loads, and describes skeletal structures as framed structures idealized as theoretical models with point joints.

2. Recap
• Structure
• Idealization of structure: 1) Discrete system 2) Continuum system 3) Hybrid
• Skeletal/Framed Structures

3. Types of Joints:
• Joint: The interconnection of members are called as joints.
• Types of Joints: 1) Pinned Joint 2) Rigid Joint 3) Internal Hinge 4) Internal
Roller 5) Free End
1) Pinned Joint: The joint which offers no restraint to rotation is called as pinned
joint. Pinned joint can transfer forces only, it cannot resists moment. It is non-
moment resisting join.
Since this joint cannot resists moment, members at this joint are free to rotate.

4. • Rigid Joint: The joint which rotates as a whole is called as rigid joint. This joint
can transfer forces as well as moments. It is a moment resisting joint.
• At this joint there may be translation in x and y direction.
• There is no relative rotation, but a single rotation is there.
• The joint rotate as a whole.
• The angle between the members remains constant even on loading.

5. • Internal Hinge: Internal hinge is considered as a joint, when inserted in a beam.
Displacement conditions are the same as that of the hinge joint.
• If internal hinge is inserted in a beam connecting two members, we can develop
one additional equilibrium equation. i.e. zero moment at the point of hinge.
• Internal Roller: Internal roller when inserted in a beam , it is considered as a
joint. When internal roller is there, there are two equilibrium equations we can
use viz. Sum of forces in the plane of roller equal to zero and moment at the
point of insertion of roller is equal to zero.
• Free End: Some times free end of the beam is also considered as a joint.

6. Classification of Structures: (Analysis)
• Determinate Structure: A structure which can be analyzed using conditions of
equilibrium alone is called as determinate structure.

7. • Indeterminate Structure: A structure which can not be analyzed by using
conditions of equilibrium alone is called as indeterminate structure. To analyze
such structure we have to develop additional equation, called as compatibility
equation. It is also called as a redundant structure.

8. • Degree of Static Indeterminacy: (Dsi)
• A statically indeterminate structure is said to have a degree of static indeterminacy
of degree of redundancy.
• A degree of static indeterminacy is the number of unknown reactions and internal
forces in excess of number of available equilibrium equations.
• The degree of static indeterminacy can be studied in two ways, Degree of internal
indeterminacy (Dsi)i and Degree of external indeterminacy (Dsi)e
• Degree of internal indeterminacy is related to the internal unknown forces and the
Degree of external indeterminacy is related to the external forces, i.e. reactions.
• Degree of external indeterminacy: (Dsi)e
• It is related to the reactions of a structure and is equal to the number of support
reactions in excess of available equilibrium equations.
(Dsi)e = R- Available equilibrium equations
Where R= No. of unknown reactions

11. Introduction
• Structure: Structure is any
construction which consists of
members or elements, Joints or
nodes, supports or constraints
and which can support external
loads and maintain equilibrium.

12. Idealization of Structures:
• According to the configuration structures are idealized as follows:
• Discrete System: A system which consists of line elements ( One-dimensional
elements) is called as discrete system. One-dimensional elements are long in
comparison to their cross-sectional dimensions. e.g. ties, columns, beams, cables
etc.
• Framed structures like continuous beams, portal frames, trusses are the examples
of discrete system.

13. • Continuum System: It consists of two-dimensional or three-dimensional
elements.
• Surface elements like plates, slabs, shells etc. are the two-dimensional elements.
These elements have surface elements large compared to their thickness.
• Volume elements consists of foundation, walls, deep beams, dams, massive
foundations which have all the dimensions significant . These are called as three-
dimensional elements.

14. • Combined System: System made of line elements and surface, or volume
elements is called as combined system or hybrid system.
• Bridge decks, beams and slabs of a building etc. are hybrid systems.

15. Skeletal Structures:
• Skeletal structures are also called as framed structures. These structures are
idealized as theoretical models with an assumption that the members behave as
one dimensional and point specifications of joints.

16. Questions:
1. Define structure with the help of neat sketch.
2. Explain: Discrete system, Continuum system and Hybrid system with the help
of neat sketch.
3. With the help of neat sketches, explain skeletal structures.