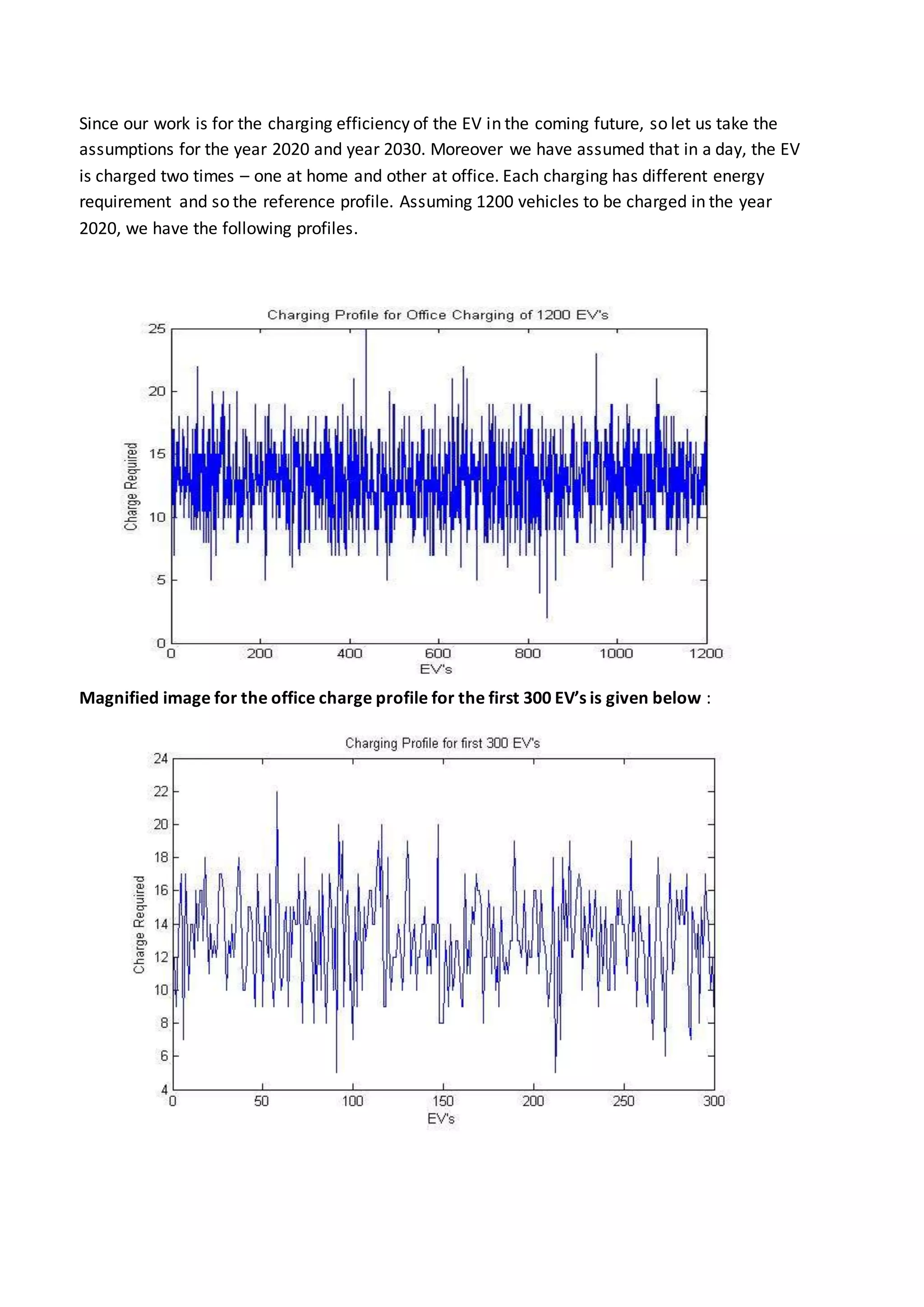
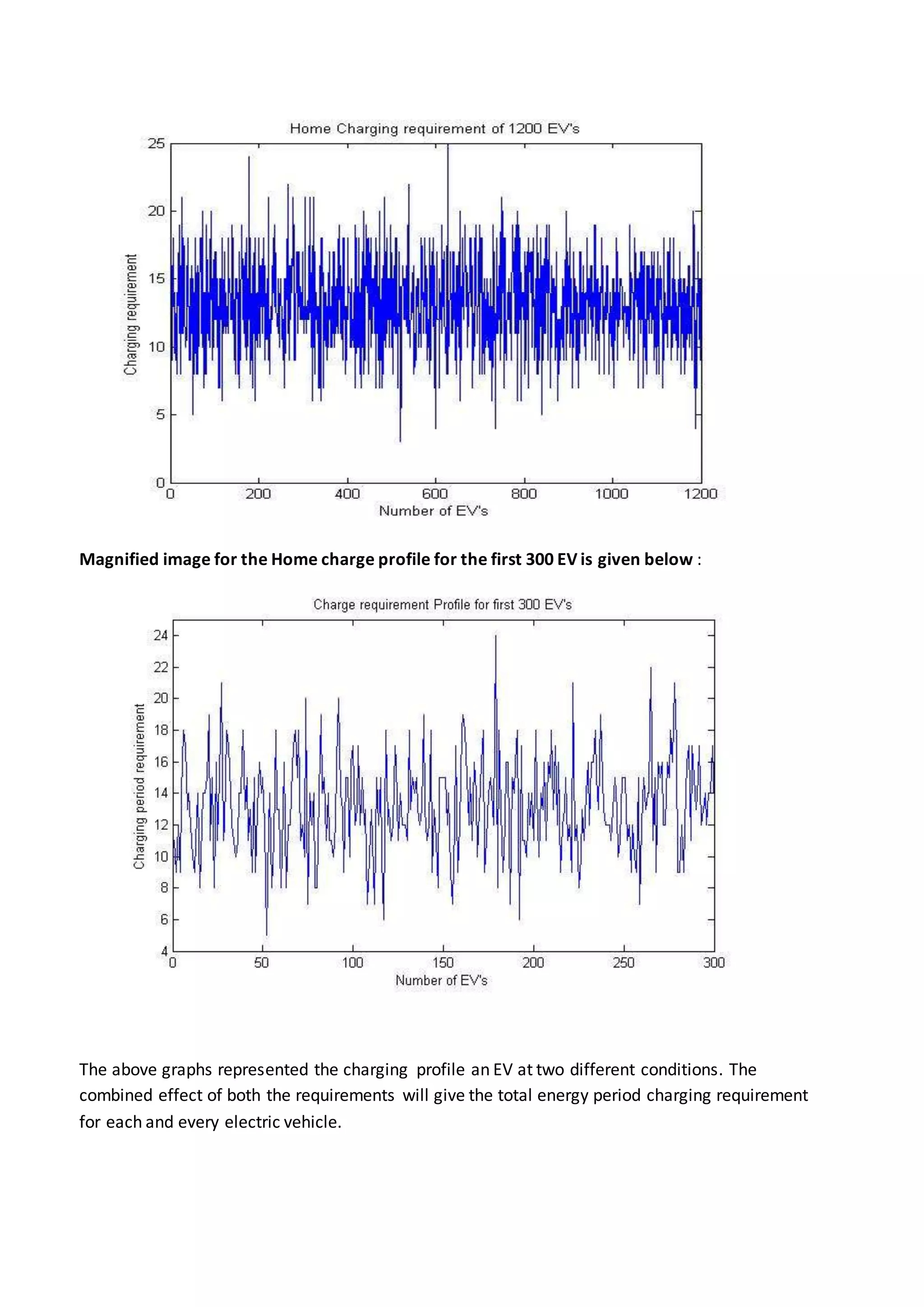
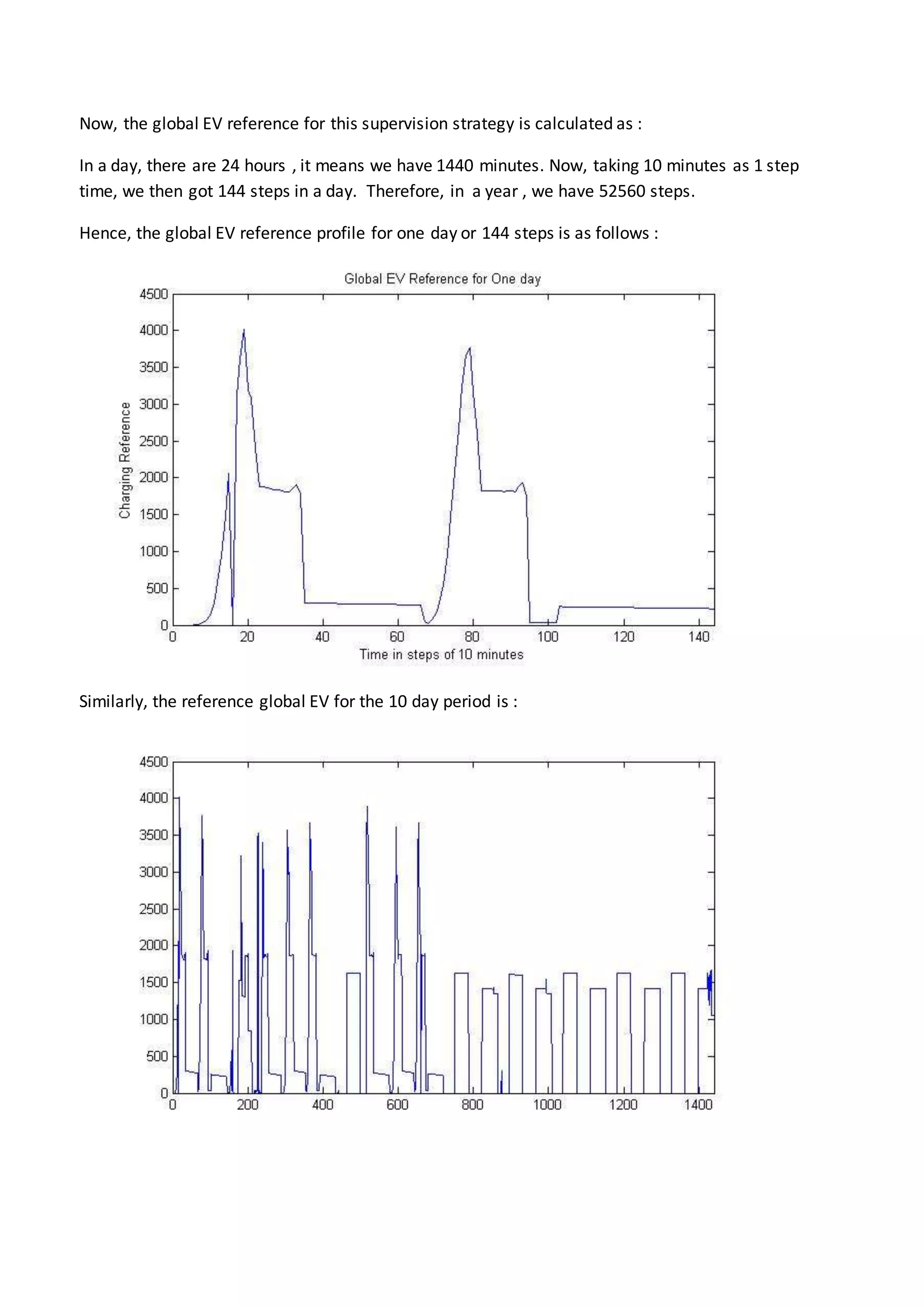
This document summarizes a student's research internship developing an algorithm for distributing electric vehicle charging commands. The aim is to find an efficient solution for scheduling EV charging at stations. The algorithm considers factors like solar and wind power availability, total energy needs, and state of charge for each EV. MATLAB code is used to simulate charging 1200 EVs over days and years, accounting for home and work charging profiles. Effects of transmission delays are also modeled by introducing time shifts to the charging schedules. Results show higher delays lead to more EVs not receiving full charges.

1. SUMMER RESEARCH INTERNSHIP –2014
Laboratoire d’electrotechniqueet d’electronique de puissance de Lille
Ecole des Hautes Etudes D’ingenieurs , Lille
A project report on
Developmentof algorithm for distribution of Electric Vehicle Charging Command
Under the supervision of
Prof. Anouar Bouallaga
Submitted by - Aman Kumar Saraf
Vellore Institute of Tehcnoligy, India

2. DEVELOPMENT OF ALGORITHM FOR DISTRIBUTION OF ELECTRIC VEHICLE
CHARGING COMMAND
The aim of the study is to find an efficient and robust solution to the electric vehicle distribution
command. Given below is the graphical representation of the EV charging distribution network
of a charging station. The EV Distribution can be defined by the arrangement of the charging
orders which are supplied to the EV at the respective charging stations during its charging. This
arrangement pattern is administered in accordance with the EV Global reference. The EV global
reference represents the maximum number of vehicles which can be charged at one step time.
In the above supervision strategy, the photovoltaic (PV) power and the wind power are
promoted to use. As this would possibly the scenario of the energy sector in the near future. This
enables the low cost and effective charging of the EV . The total energy and the State of Charge
of the EV is measured and estimated. This estimation is then conferred in accordance with the
EV global reference to make a matrix of the EV Charging distribution orders.

3. Since our work is for the charging efficiency of the EV in the coming future, so let us take the
assumptions for the year 2020 and year 2030. Moreover we have assumed that in a day, the EV
is charged two times – one at home and other at office. Each charging has different energy
requirement and so the reference profile. Assuming 1200 vehicles to be charged in the year
2020, we have the following profiles.
Magnified image for the office charge profile for the first 300 EV’s is given below :

4. Magnified image for the Home charge profile for the first 300 EV is given below :
The above graphs represented the charging profile an EV at two different conditions. The
combined effect of both the requirements will give the total energy period charging requirement
for each and every electric vehicle.

5. Now, the global EV reference for this supervision strategy is calculated as :
In a day, there are 24 hours , it means we have 1440 minutes. Now, taking 10 minutes as 1 step
time, we then got 144 steps in a day. Therefore, in a year , we have 52560 steps.
Hence, the global EV reference profile for one day or 144 steps is as follows :
Similarly, the reference global EV for the 10 day period is :

6. MATLAB CODE :
clear all
close all
clc
annee=2020;
switch annee
case 2020
load profil_ve_20
load temps_arrive_1200
load Nb_etat_tr
load Nb_etat_dom
vei=round(profil_ve(1:52560,1)/3.7);
M_vei=zeros(144,365);
for i=1:365
M_vei(:,i)=vei(144*(i-1)+1:144*i);
if sum(M_vei(:,i))<sum(Nb_etat_tr+Nb_etat_dom)
M_vei(:,i)=round(M_vei(:,i)*(sum(Nb_etat_tr+Nb_etat_dom)/sum(M_vei(:,i))));
end
end
nb_ve=1200;
case 2030
load Nb_etat_tr_30
load Nb_etat_dom_30
load profil_ve_30
load temps_arrive_1200
vei=round(profil_ve(1:52560,1)/3.7);
M_vei=zeros(144,365);
for i=1:365
M_vei(:,i)=vei(144*(i-1)+1:144*i);
if sum(M_vei(:,i))<sum(Nb_etat_tr+Nb_etat_dom)
M_vei(:,i)=round(M_vei(:,i)*(sum(Nb_etat_tr+Nb_etat_dom)/sum(M_vei(:,i))));
end
end
nb_ve=1200
end
Tve=[];
Pr_nw=[];
ref= []; % jours
Be=[];
A=[];
B=[];
ordre=[];
VE=[];
for m=1:2
m
Y_tr =zeros(nb_ve,144);
Y_dom =zeros(nb_ve,144);

7. Nb_etat_dom_i= zeros(nb_ve,1);
Nb_etat_tr_i= zeros(nb_ve,1);
vei_tr=M_vei(1:66,m);
vei_dom=M_vei(67:144,m);
if sum(vei_tr)<sum(Nb_etat_tr)
vei_tr=round(vei_tr*(sum(Nb_etat_tr)/sum(vei_tr))+0.5);
end
if sum(vei_dom)<sum(Nb_etat_dom)
vei_dom=round(vei_dom*(sum(Nb_etat_dom)/sum(vei_dom))+0.5);
end
ve_rep=[vei_tr ; vei_dom ];
g=[vei_tr ; vei_dom ];
ref= [ref;g] ;
limit_tr=66;
limit_dom=144;
or = zeros (nb_ve,1);
a= zeros (143,1);
BEd=(Nb_etat_tr+Nb_etat_dom);
%***********************Chargement_travail*********************************
[bs_tr, b_tr] = sort(Nb_etat_tr,'descend');
for j=1:66
j;
for k=1:nb_ve
i=b_tr(k);
if sum(Y_tr(i,:))<Nb_etat_tr(i,1) && debut_tr(i)<=j
if ve_rep(j)>0
ve_rep(j)= ve_rep(j)-1;
Y_tr(i,j)=1;
else if Nb_etat_tr(i)- ((limit_tr-j)+sum(Y_tr(i,:)))>0
ve_rep(j)= ve_rep(j)-1;
Y_tr(i,j)=1;
else
Y_tr(i,j)=0;
end
end
end
end
end
%************************Chargement_domicile*******************************
[bs_dom, b_dom] = sort(Nb_etat_dom,'descend');
for j=67:144
j;
for k=1:nb_ve
c=0;
i=b_dom(k);

8. if sum(Y_dom(i,:))<Nb_etat_dom(i,1) && debut_dom(i)<=j
if ve_rep(j)>0
ve_rep(j)= ve_rep(j)-1;
Y_dom(i,j)=1;
else if Nb_etat_dom(i)- ((limit_dom-j)+sum(Y_dom(i,:)))>0
ve_rep(j)= ve_rep(j)-1;
Y_dom(i,j)=1;
else
Y_dom(i,j)=0;
end
end
end
end
end
%**************************ORDRES******************************************
Ytotale = Y_tr+Y_dom;
c=0;
for i=1:nb_ve
for j=1:143
a(j)=Ytotale(i,j+1)-Ytotale(i,j);
if a(j)~=0
c=c+1;
end
end
or(i)=c;
c=0;
end
%**************************VE**********************************************
VEc=0;
BEr=(sum(Ytotale'))';
dif= BEd-BEr;
for i=1:nb_ve
if dif(i)~= 0
VEc=VEc+1;
end
end
VE =[VE VEc];
ordre= [ordre or];
Pr_nw=[ Pr_nw sum(Y_tr+Y_dom) ];
A = [A (sum(Y_tr'))' ];
B = [B (sum(Y_dom'))'];
end
Pr=sum(Pr_nw) ;
Be=[Be A+B ];
Prefd=ref';
%***********************Indicateurs****************************************
err_ve=100*(((Pr)-sum(Prefd))/sum(Prefd))
err_final = 100*((sum(Pr) - sum(Prefd))/sum(Prefd))
err_BE=100*((sum(sum( Be))-
m*sum(Nb_etat_tr+Nb_etat_dom))/(m*sum(Nb_etat_tr+Nb_etat_dom)))

9. VEcmoy= mean(VE)
ordre_moy=mean((sum(ordre'))')
%***********************Affichage******************************************
plot (Pr_nw)
hold on
grid on
plot(Prefd,'r')
Graphs :
Input and output for 2 & 10 days :

10. Real time charging
In real time applications, The simulation may get sometime gets deviated from the real results.
Since, our work is related with the transmission lines and all the data are transferred
electronically, it may develop some error due to the time delay. Therefore, we have introduced
some time delay algorithms in our work.
APPROACH ------
MATLAB CODE
Apply Delay which circullay shifts
the 1 or 0 by the delay amount
plot the results

11. MATLAB CODE FOR THE DELAY :
%%%%%%%% Chargement retard %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
retard_tr = zeros(1200,2);
retard_dom = zeros(1200,2);
for i = 1:1200
for j = 1:66
l = i;
if Y_tr(i,j) == 1
retard_tr(l,1) = j;
break;
end
end
end
for i = 1:1200
for j = 67:144
l = i;
if Y_dom(i,j) == 1
retard_dom(l,1) = j;
break;
end
end
end
taille =1200;
if taille>=1
for l = 1:taille
retard_tr(l,2) = 6 ;
retard_dom(l,2) = 6 ;
end
for l = taille+1:1200
retard_tr(l,2) = 0;
retard_dom(l,2) = 0;
end
Yfinal_tr = Y_tr;
Yfinal_dom = Y_dom;
for l = 1:taille
i = b_tr(l);
j = retard_tr(l,1);
Yfinal_tr(i,j:end) = circshift(Yfinal_tr(i,j:end),[0 retard_tr(l,2)]);
for j = retard_tr(l,1):retard_tr(l,1)+retard_tr(l,2)-1
Yfinal_tr(i,j) = 0;
end
end
for l = 1:taille
i = b_dom(l);
j = retard_dom(l,1);
Yfinal_dom(i,j:end) = circshift(Yfinal_dom(i,j:end),[0 retard_dom(l,2)]);
for j = retard_dom(l,1):retard_dom(l,1)+retard_dom(l,2)-1

12. Yfinal_dom(i,j) = 0;
end
end
end
Ytotale = Y_tr+Y_dom;
for j=1:1200
for k=67:144
if Yfinal_tr(j,k)==1;
Yfinal_tr(j,k)=0;
end
end
end
Yfinal = Yfinal_tr(:,1:144)+Yfinal_dom(:,1:144);
for i =1:1200
not_char_work(i,1)=sum(Yfinal(i,1:144));
req_work(i,1)=sum(Ytotale(i,1:144));
end
final_work{m} = sum(req_work) - sum(not_char_work);
ve_delay_work{m} = sum(Yfinal(:,1:144));
dif=zeros (1200,1);
T=0;
BEr=(sum(Ytotale'))';
BEfinal=(sum(Yfinal'))';
dif=BEr-BEfinal;
for i=1:1200
if dif(i)~= 0
T=T+1;
end
end
Tve=[Tve T];
final_last_work = cell2mat(final_work);
ve_delay_last_work = cell2mat(ve_delay_work);
veh_not_char_work{m} = nnz(final_last_work(:,m));
data_1 = cell2mat(veh_not_char_work);
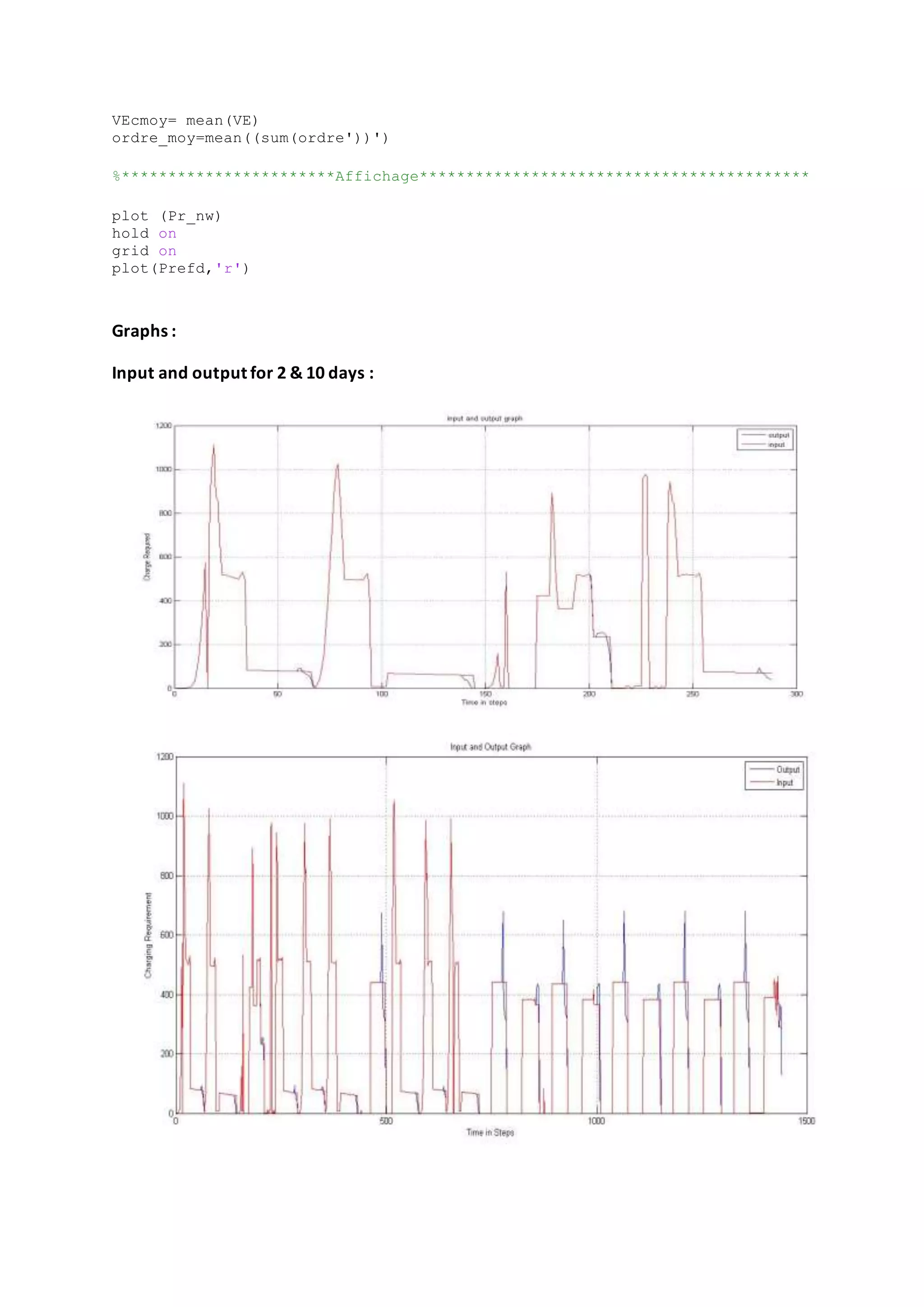
The above code is concatenated with the above previous matlab code to get the full code
with the delay to get the idea of the real analysis of the data transmitted through the full
process.
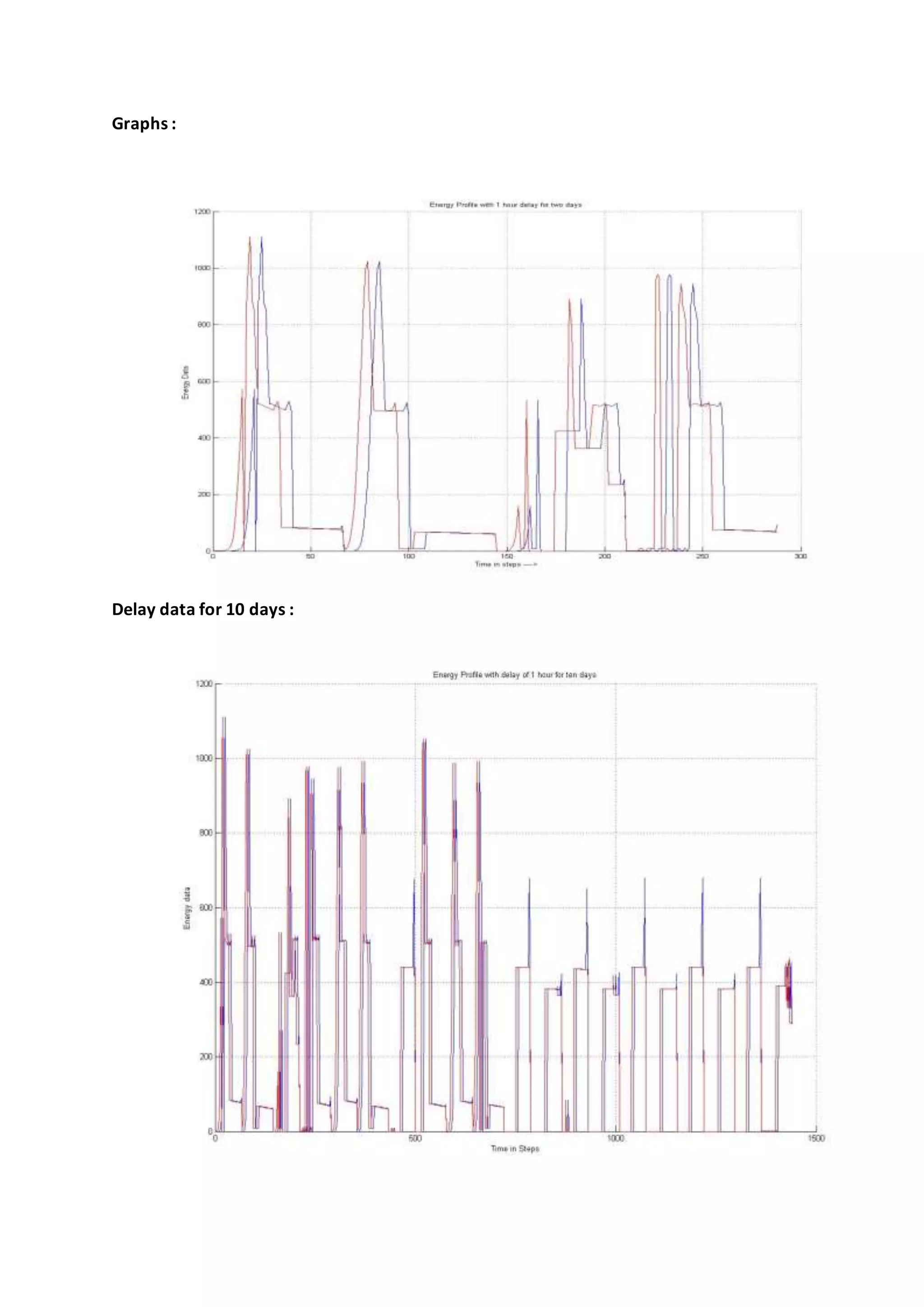
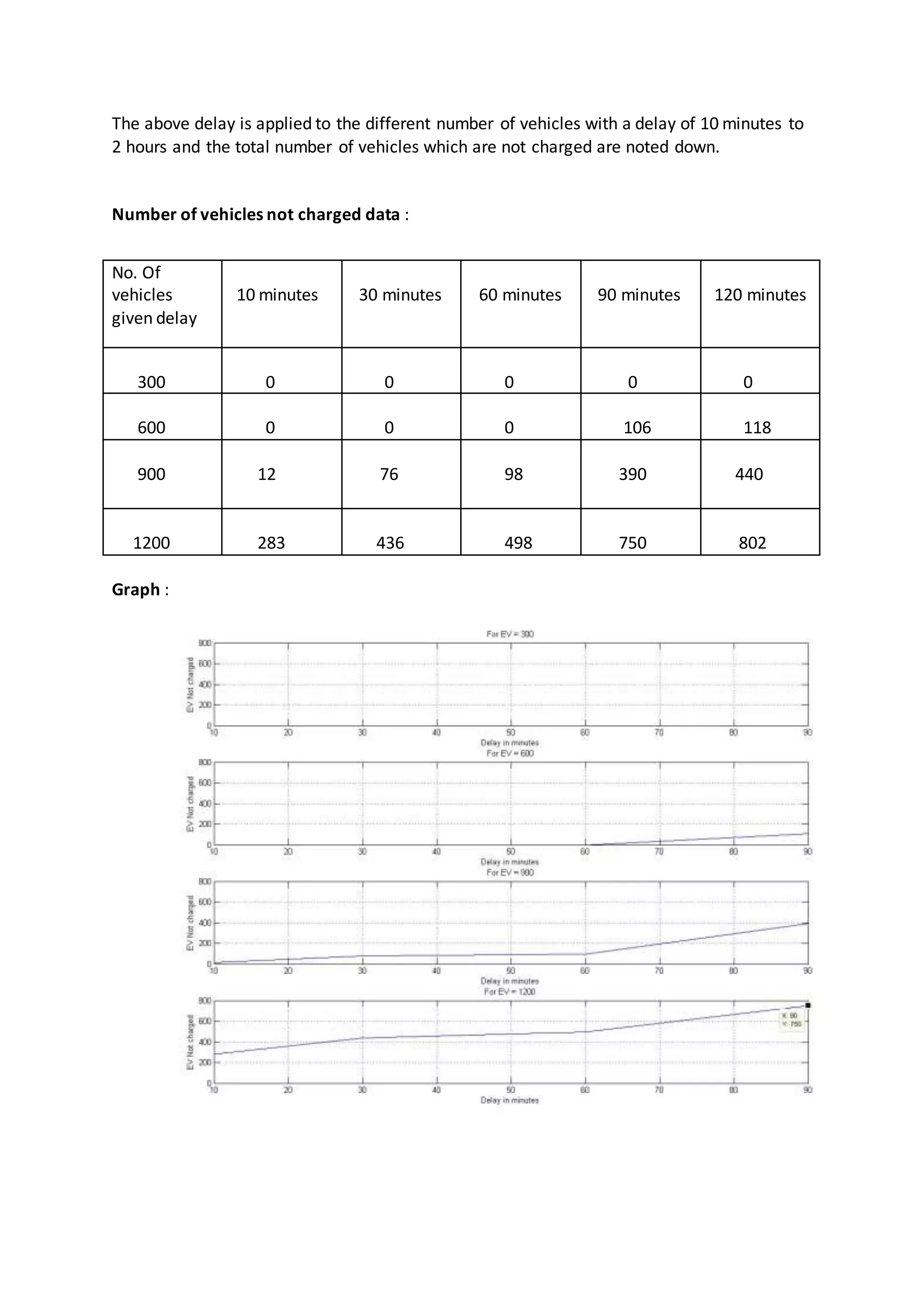
The delay is applied for the two and ten days and the graph is plotted and the number of
vehicles which are not charged are collected.

13. Graphs :
Delay data for 10 days :

14. The above delay is applied to the different number of vehicles with a delay of 10 minutes to
2 hours and the total number of vehicles which are not charged are noted down.
Number of vehicles not charged data :
Graph :
No. Of
vehicles
given delay
10 minutes 30 minutes 60 minutes 90 minutes 120 minutes
300 0 0 0 0 0
600 0 0 0 106 118
900 12 76 98 390 440
1200 283 436 498 750 802

15. CONCLUSION :
The above study dealt with the efficient and cost effective charging of the Electric Vehicle.
From the simulation results it is concluded that the model is very effective for the delay up
to 900 vehicles. It is also concluded that the number of vehicles which are not charged rises
significantly after 1 hour delay. The range of vehicles being from 0 % to 37 % of the total
capacity. But, if the delay is provided for further vehicles, that percentage stars ranging from
24 % to 67 % .