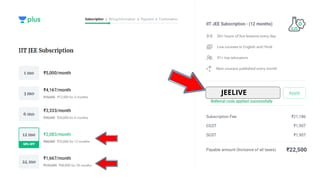
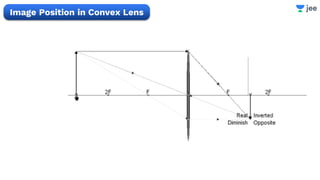
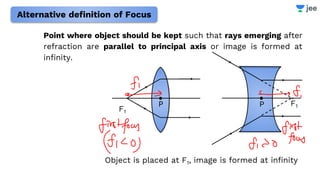
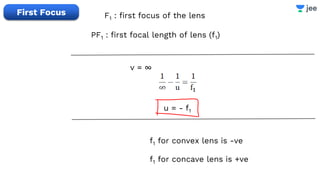
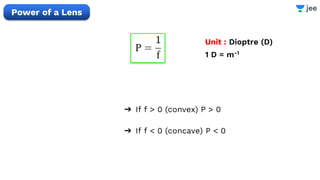
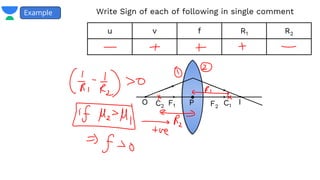
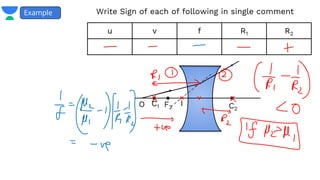
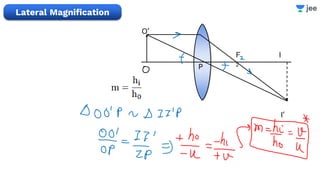
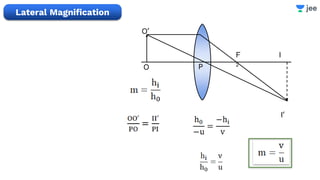
- The document discusses key concepts in ray optics and lens formula including different types of lenses, focal length, lens maker's formula, and image formation using lenses. - It provides examples of problems calculating focal length, image position and size, and power of lenses using the lens formula and definitions of focal length. - The document is a lecture on lens formula and ray optics by an experienced physics educator, providing an overview of core concepts and examples to help students learn.

1. Lens Formula Ray Optics:
Lenses
Lecture - 1

2. Jayant Nagda
Physics Educator
unacademy.com/@JayantNagda
B.Tech, IIT Bombay
IIT-JEE AIR - 161
9+ Years of Teaching Experience at
3 Coaching Institutes (multiple under 15 AIRs)
In top 1% INPhO

3. unacademy.com/plus
Live & Recorded Lectures
Personalized Interaction
Quizzes & Test Series
Dedicated Doubt Sessions

4. JEELIVE

5. PLUS Courses

6. Step 1 Step 2
INSTALL

7. Step 3 Step 4

8. Step 6
JEELIVE
Step 5

9. Lens
Converging (or) Convex Lens
Diverging (or) Concave Lens

10. Image Position in Convex Lens

11. Image Position in Convex Lens

12. Image Position in Concave Lens

13. Lens A lens is a homogenous transparent medium
(such as glass) bounded by two curved surfaces
or one curved and one plane surface.
R2 R1
C1
C2 P

14. Lens Types of Lens
BiConvex or Convex lens Biconcave or Concave
lens
Converging Lens Diverging Lens
EquiConvex if R1 = R2 EquiConcave if R1 = R2

15. Plano-Concave lens Concavo-Convex lens
Plano-Convex lens
Types of Lens

16. R2 R1
C1
C2 P
C1, C2 : Centre of curvature of 1st & 2nd surface
R1, R2 : Radius of curvature of 1st & 2nd surface
Principal axis : line joining C1 & C2
Centre of lens P also known as Optical centre
Lens Terms

17. O P
μ1 μ1
μ2
C1 C2
Refraction at 1st surface

18. O I
P
μ1 μ1
μ2
C1 C2
Refraction at 1st surface
Refraction at 2nd surface
Adding 1 & 2
1
2

19. If object is kept at ∞, its image is formed at f
If u ➝ ∞ , v = f
Lens Maker’s formula
Lens Maker’s Formula
(Definition of Focus)

20. Write Sign of each of following in single comment
Example
O I
P
F1 C1
F2
C2
u v f R1 R2

21. Example
O I
C1 F2 C2
u v f R1 R2
Write Sign of each of following in single comment

22. Find the focal length of lens
Example
10 cm
10 cm
1.5
Numerical Answer Type Question [ +4 , 0]

23. Find the focal length of lens
Example
1.5
10 cm
10 cm
Numerical Answer Type Question [ +4 , 0]

24. Find the focal length of lens
Example
μ = 2
20 cm
μ = 1
Numerical Answer Type Question [ +4 , 0]
20 cm

25. Lens formula
1. Same medium on both side of lens μ1 , lens medium of μ2
2. Thin lens, thickness is negligible as compared to object distance.
3. Light rays are Paraxial
Lens Formula
To be applied keeping in mind:

26. Focus of Lens
Point where parallel incident rays will intersect after refraction.
If object is kept at infinity its image will be at focus.
Convex Lens
(or)
Converging Lens
Concave Lens
(or)
Diverging Lens
F2
P
F2

27. F2 : second focus of lens
PF2 : second focal length (f2)
As u = ∞ then
⇒ v = f
Second Focus
Second focal length f2 is +ve for convex lens
-ve for concave lens

28. By lens Maker’s formula
For convex lens R1 > 0 & R2 < 0 So,
and as long as μ2 > μ1 , f will also be +ve
For concave lens R1 < 0 & R2 > 0 so, f is -ve
Second focal length f2 is +ve for convex lens
-ve for concave lens
Second Focus

29. Alternative definition of Focus
Point where object should be kept such that rays emerging after
refraction are parallel to principal axis or image is formed at
infinity.
P F1
P
Object is placed at F1, image is formed at infinity
F1

30. F1 : first focus of the lens
PF1 : first focal length of lens (f1)
v = ∞
u = - f1
f1 for convex lens is -ve
f1 for concave lens is +ve
First Focus

31. Example
Concave lens of focal length 20 cm has object placed 12 cm
from it. Determine position of image.
A. 12.5 cm B. -9.5 cm D. 11 cm
C. -7.5 cm
MCQ type Question [ +4 , -1]

32. Lateral Magnification
P
O’
F
2
I
I’

33. Lateral Magnification
P
O
O’
F
2
I
I’

34. Example
Convex lens of focal length 15 cm has object kept at 45 cm
from it. If height of Object is 15cm determine, position and
height of Image.
Numerical Answer Type Question [ +4 , 0]

35. Example
A. 25 m/s B. 15 m/s D. 5 m/s
C. 45 m/s
f = 30 cm
20 cm
5 m/s
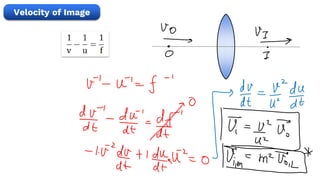
Find velocity of image of Object O shown
MCQ type Question [ +4 , -1]

36. Velocity of Image

37. Power of a Lens
Unit : Dioptre (D)
1 D = m-1
➔ If f > 0 (convex) P > 0
➔ If f < 0 (concave) P < 0

38. Example Find power, if f = 50 cm
A. + 1 D B. - 1 D C. + 2D D. + 3D

39. Daily Practice Problems

40. Find f
Example
60 cm 15 cm
1.5
A. 20 cm B. 18 cm D. 24 cm
C. 12 cm
MCQ type Question [ +4 , -1]

41. Example
f = 15 cm
45 cm
O
A. 22.5, +2.5 B. 23.5, +1.5 D. 20.5, +1.5
C. 22.5, -2.5
Determine position & height of image when Object is
5cm high kept as shown:
MCQ type Question [ +4 , -1]

42. Example
f = 12 cm
32 cm
Find position of object for which Image is formed 32 cm from
lens
A. 22.5 B. 17.5
D. 20
C. 19.2
MCQ type Question [ +4 , -1]

43. Example
Concave lens of focal length 20cm has object of height 2 cm
at 10 cm from it. Determine position and height of Image
formed?
Ans:
u = -10 cm,
h0 = 2 cm,
f = -20 cm,
v = -20/3 cm,
hi = +4/3cm
Numerical Answer Type Question [ +4 , 0]

44. Example
Find the position where convex lens of focal length 9cm
must be placed so that the image of both Objects is
formed at same place
O1 O2
24 cm
9 cm
18 cm from O1
Numerical Answer Type Question [ +4 , 0]

45. Convex lens made of glass (1.5) of focal length 50 cm is
immersed in water μ = 4/3. What is its focal length in water?
Example Numerical Answer Type Question [ +4 , 0]
Ans: 100 cm

46. Convince yourself that focal length derived by lens maker’s
formula is second focal length using sign of R1 & R2
Example

47. Which of the following statements is correct?
Example
A. When a lens is dipped in water, magnitude of its focal length
increases.
B. When a lens is dipped in water, magnitude of its focal length
decreases.
C. When a spherical mirror is dipped in water, magnitude of its
focal length increases.
D. None of these
Ans : A

48. An object is placed at a distance m times the focal length of
a divergent lens. The size of the image is shorter than that
of the object by
Example
A. m times B. (m + 1) times
C. (m –1) times D. m2 times
Ans : B

49. A thin lens is made with a material having refractive index
μ = 1.5. Both the sides are convex. It is dipped in water (μ =
1.33). It will behave like
Example
A. a convergent lens B. a divergent lens
C. a rectangular slab D. a prism
Ans : A

50. A double convex lens made of material of refractive index 1.5 and
having a focal length of 10 cm is immersed in a liquid of refractive
index 3.0. The lens will behave as
Example
A. Converging lens of focal length 10 cm
B. diverging lens of focal length 10 cm
C. converging lens of focal length 10/3 cm
D. converging lens of focal length 30 cm.
Ans : B

51. A converging lens of focal length f is placed at a distance 0.3 m
from an object to produce an image on a screen 0.9 m from the
lens. With the object and the screen in the same positions, an
image of the object could also be produced on the screen by
placing a converging lens of focal length
Example
A. f at a distance 0.1 m from the screen
B. f at a distance 0.3 m from the screen
C. 3 f at a distance 0.3 m from the screen
D. 3 f at a distance 0.1 m from the screen
Ans : B

52. A convex lens focuses a distant object 40 cm from it on a
screen placed 10 cm away from it. A glass plate (μ = 1.5) and
of thickness 3 cm is inserted between the lens an the
screen. Where the object should be placed so that its image
is again focused on the screen ?
Example
Ans : B
A. 62 cm B. 72 cm
C. 52 cm D. 42 cm

53. A convex lens of focal length 15 cm is placed coaxially in
front of a convex mirror. The lens is 5 cm from the apex of
the mirror. When an object is placed on the axis at a
distance of 20 cm from the lens, it is found that the image
coincides with the object. Calculate the radius of curvature
of the mirror.
Example
A. 45 cm B. 85 cm
C. 65 cm D. 55 cm
Ans : D

54. A convex lens makes a real image 4 cm long on a screen.
When the lens is shifted to a new position without
disturbing the object or the screen, we again get real image
on the screen which is 9 cm long. The length of the object
must be
Example
A. 2.25 cm B. 36 cm
C. 6 cm D. 6.5 cm
Ans : C

57. tinyurl.com/jeelivechat
Telegram
APP