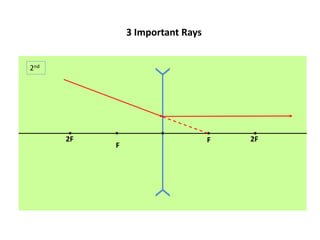
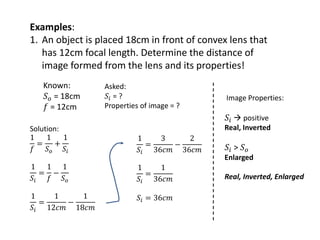
The document discusses concepts related to lenses including: 1) Convex and concave lenses form real or virtual images depending on whether the light rays converge or diverge after passing through the lens. 2) Important lens formula relates the focal length, object distance, and image distance. 3) Properties of images formed by convex and concave lenses such as magnification, orientation, and size are determined using the lens formula and relationships between object and image distances.

1. Converging and Diverging

2. Convex Lens

3. 3 Important Rays
1st
2F 2F
F
F

4. 3 Important Rays
2nd
2F 2F
F
F

5. 3 Important Rays
3rd
2F 2F
F
F

6. Forming an Image on Convex Lens
2F 2F
F
F
object
image
• The important rays actually do come together to form the image  Real Image
• To see the image, we need to put screen in the location of the image
• Properties of image: Real, Inverted, Diminished

7. Object Convex Lens
Real Image
Screen

8. Forming an Image on Convex Lens
2F 2F
F
F
object
image
• Properties of image: Real, Inverted, Enlarged

9. Forming an Image on Convex Lens
2F 2F
F
F object
image
• The image appears when the important rays don’t come together, but the
extensions do  Virtual Image
• Properties of image: Virtual, upright enlarged
observer

10. Seeing virtual image through convex lens…

11. Concave Lens

12. 1st
2F 2F
F
F
3 Important Rays

13. 2nd
2F 2F
F
F
3 Important Rays

14. 3rd
2F 2F
F
F
3 Important Rays

15. 2F 2F
F
F
Forming an image on concave lens
object image
• Properties of image: Virtual, Upright, Diminished

16. 2F 2F
F
F
Forming an image on concave lens
object image
• Properties of image: Virtual, Upright, Diminished

17. 2F 2F
F
F
Forming an image on concave lens
object
image
• Properties of image: Virtual, Upright, Diminished

18. In concave lens, there is only one type
of image:
Virtual ,Upright, Diminished

19. Formula of Lenses
• In lenses, the distance of the object from its pole is called
the object distance (So).
• The distance of the image from the pole of the lens is
called the image distance (Si).
• The distance of the principal focus from the pole is called
the focal length (f).
There is a relationship between these three quantities given
by the lens formula which is expressed as:
𝟏
𝒇
=
𝟏
𝑺𝟎
+
𝟏
𝑺𝒊

20. 𝟏
𝒇
=
𝟏
𝑺𝟎
+
𝟏
𝑺𝒊
Note that in this formula:
 So must be positive.
 If Si is negative (-), then the image is virtual. If Si is positive (+),
then the image is real.
 In convex lens, the focal length value is positive (f = +)
 In concave lens, the focal length value is negative (f = -)
 The focal length is half of radius of curvature (R), which value
(f = R/2)

21. Examples:
1. An object is placed 18cm in front of convex lens that
has 12cm focal length. Determine the distance of
image formed from the lens and its properties!
Known:
𝑆𝑜 = 18cm
𝑓 = 12cm
Solution:
1
𝑓
=
1
𝑆𝑜
+
1
𝑆𝑖
1
𝑆𝑖
=
1
𝑓
−
1
𝑆𝑜
1
𝑆𝑖
=
1
12𝑐𝑚
−
1
18𝑐𝑚
1
𝑆𝑖
=
3
36𝑐𝑚
−
2
36𝑐𝑚
1
𝑆𝑖
=
1
36𝑐𝑚
𝑆𝑖 = 36𝑐𝑚
Asked:
𝑆𝑖 = ?
Properties of image = ?
Image Properties:
𝑆𝑖  positive
Real, Inverted
𝑆𝑖 > 𝑆𝑜
Enlarged
Real, Inverted, Enlarged

22. Examples:
2. An object is placed 24cm in front of concave lens that
has 8cm focal length. Determine the distance of
image formed from the lens and its properties!
Known:
𝑆𝑜 = 24cm
𝑓 = -8cm
Solution:
1
𝑓
=
1
𝑆𝑜
+
1
𝑆𝑖
1
𝑆𝑖
=
1
𝑓
−
1
𝑆𝑜
1
𝑆𝑖
=
1
−8𝑐𝑚
−
1
24𝑐𝑚
1
𝑆𝑖
=
−3
24𝑐𝑚
−
1
24𝑐𝑚
1
𝑆𝑖
=
−4
24𝑐𝑚
𝑆𝑖 = −6𝑐𝑚
Asked:
𝑆𝑖 = ?
Properties of image = ?
Image Properties:
𝑆𝑖  negative
Virtual , Upright
𝑆𝑖 < 𝑆𝑜
Diminished
Virtual, Upright,
Diminished

23. Magnification of Image (M)
• Magnification produced by a lens means the ratio of the height of
the image to the height of the object.
• It is usually represented by the letter M.
• If ho is the height of the object and hi is the height of the image,
then the magnification M produced by lens is given by:
𝑴 =
𝒉𝒊
𝒉𝒐
=
𝒔𝒊
𝒔𝒐

24. 𝑴 =
𝒉𝒊
𝒉𝒐
=
𝒔𝒊
𝒔𝒐
NOTE:
 The value of M, must be positive.
 The height of the object is taken to be positive as the object is
usually placed above the principal axis.
 If M > 1, then the image is magnified
 If M < 1, then the image is diminished
 If M = 1, then the image are the same size as the object.

25. Examples:
1. A candle with 3cm height is placed 6 cm in front of convex lens. If the focal
length of the convex lens is 4cm, determine:
a. The location of image from the lens (𝑆𝑖)
b. The magnification of image (M)
c. The height of the image (ℎ𝑖)
Known:
𝑆𝑜 = 6cm
ℎ𝑜 = 3cm
𝑓 = 4cm
Asked:
𝑆𝑖 = ?
M =?
ℎ𝑖 = ?
Solution:
1
𝑓
=
1
𝑆𝑜
+
1
𝑆𝑖
1
𝑆𝑖
=
1
𝑓
−
1
𝑆𝑜
1
𝑆𝑖
=
1
4𝑐𝑚
−
1
6𝑐𝑚
1
𝑆𝑖
=
3
12𝑐𝑚
−
2
12𝑐𝑚
1
𝑆𝑖
=
1
12𝑐𝑚
𝑺𝒊 = 𝟏𝟐𝒄𝒎
𝑀 =
𝑆𝑖
𝑆𝑜
𝑀 =
12𝑐𝑚
6𝑐𝑚
𝑴 = 𝟐
The image is two times larger
than object
𝑀 =
ℎ𝑖
ℎ𝑜
2 =
ℎ𝑖
3𝑐𝑚
𝒉𝒊 = 𝟔𝒄𝒎

26. Examples:
2. A candle with 6cm height is placed 12cm in front of concave lens. If the focal
length of the concave lens is 4cm, determine:
a. The location of image from the lens (𝑆𝑖)
b. The magnification of image (M)
c. The height of the image (ℎ𝑖)
Known:
𝑆𝑜 = 12cm
ℎ𝑜 = 6cm
𝑓 = -4cm
Asked:
𝑆𝑖 = ?
M =?
ℎ𝑖 = ?
Solution:
1
𝑓
=
1
𝑆𝑜
+
1
𝑆𝑖
1
𝑆𝑖
=
1
𝑓
−
1
𝑆𝑜
1
𝑆𝑖
=
1
−4𝑐𝑚
−
1
12𝑐𝑚
1
𝑆𝑖
=
−3
12𝑐𝑚
−
1
12𝑐𝑚
1
𝑆𝑖
=
−4
12𝑐𝑚
𝑺𝒊 = −𝟑𝒄𝒎
𝑀 =
𝑆𝑖
𝑆𝑜
𝑀 =
−3𝑐𝑚
12𝑐𝑚
𝑴 =
𝟏
𝟒
The image is four times smaller
than object
𝑀 =
ℎ𝑖
ℎ𝑜
1
4
=
ℎ𝑖
6𝑐𝑚
𝒉𝒊 = 𝟏. 𝟓𝒄𝒎

27. Exercise:
1. A 6cm candle is placed 12 cm in front of convex lens. The focal
length of the convex lens is 8cm. Determine:
a) the location of the image formed (𝑆𝑖)
b) the magnification of image (M)
c) the height of the image (ℎ𝑖)
2. A 10 cm light bulb is placed 15cm from a concave lens that has a
focal length of 10 cm. Determine:
a) the location of the image formed (𝑆𝑖)
b) the magnification of image (M)
c) the height of the image (ℎ𝑖)
3. When a candle is placed 24 cm in fornt of convex lens, a real image is
produced and it is only half sized of the object (two times smaller).
What will be the properties of the image if the object is placed 6cm
from the convex lens?

28. Link: https://www.youtube.com/watch?v=T-iy29oEmSI
• When a light ray reaches the boundary between two
transparent materials it may be refracted.
• If it is leaving the more dense medium, this refraction
would be expected to bend the ray away from the normal
as it emerges.
• However, if this would bend the ray at more than 90° from
the normal, the refraction is not possible.
Critical angle and total internal reflection

29. • In this situation, the ray is reflected inside the more dense
medium, following the law of reflection.
• This is called total internal reflection (TIR).
• The angle of incidence when the angle of refraction is 90o,
and the ray changes from just refracting to total internal
reflection, is called the critical angle.
Link: https://www.youtube.com/watch?v=NAaHPRsveJk&t=33s

30. Application of Total Internal Reflection
Link: https://www.youtube.com/watch?v=Lic3gCS_bKo