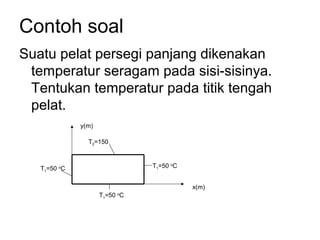
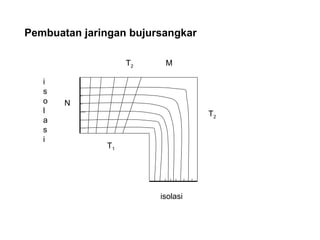
Dokumen ini membahas tentang konduksi panas dalam sistem homogen dan mencakup persamaan umum serta penyelesaian analitik untuk distribusi suhu pada kondisi stabil. Selain itu, dijelaskan metode grafik untuk memvisualisasikan aliran panas dan contoh soal terkait perhitungan temperatur serta faktor bentuk pada situasi nyata seperti pipa penyalur crude-oil. Pemisahan variabel dan metode lain digunakan untuk menyelesaikan persamaan dan menghitung laju aliran panas.

1. KONDUKSI STEDI,
Dimensi Rangkap.
Pertemuan ke 6

2. Persamaan umum konduksi panas
untuk sistem homogen dan 2 D :
 ∂2T ∂2T  1 ∂T
 2 + 2
 ∂x =
 α ∂t
Cartesian’s coordinate
 ∂y 
 ∂ 2T  1 ∂ T  ∂ 2T  1 ∂ T silinder
 2 +
 ∂r  r ∂r + 2 =
 ∂z  α ∂t
   
Dimana ,
α = k / c.ρ

3. Penyelesaian analitik
Distribusi suhu umumnya pada kondisi stedi-
state : 2
∂T 2
∂T
+ 2 =0
∂x 2
∂y
T = f (x,y) = X(x). Y(y)
Sehingga :
1 ∂2 X 1 ∂2Y = λ2
− =
X ∂ 2
x Y ∂ 2
y

4. Dengan pemisahan variabel :
d2X d 2Y
+ λ2 X = 0 −λY =0
2
dx 2 dy 2
X = A cos λx + B sin λx
−λy λy
Y = Ce + De
Solusi umum, diselesaikan dari boundary conditions :
− λy λy
T = ( A cos λx + B sin λx)(Ce + De )

5. Contoh soal
Suatu pelat persegi panjang dikenakan
temperatur seragam pada sisi-sisinya.
Tentukan temperatur pada titik tengah
pelat.
y(m)
T2=150
T1=50 oC T1=50 oC
x(m)
T1=50 C
o

6. 2. Metode Grafik
• Membuat jaringan isoterm
• Aliran panas tegak lurus dengan garis
isoterm.
• Garis isoterm dan garis aliran panas
berbentuk bujursangkar. Penggambaran
dengan tangan dan coba-coba. Makin
dekat dengan bentuk bujursangkar makin
baik.

7. Pembuatan jaringan bujursangkar
T2 M
i
s
o N
l T2
a
s
i
T1
isolasi

8. Laju Aliran Panas (Hk. Fourier)
Laju aliran panas
∆T
∆q = −k (∆l.1) = −k .∆T
∆l
T2 −T1
∆T =
N
m= M
M
q = ∑ ∆ qm = k (T2 − T1 )
m=1 N

9. FAKTOR BENTUK
Persamaan aliran panas berdasarkan metode grafik
dapat dinyatakan dalam :
q =kS .∆T
S = faktor bentuk , lihat tabel 3.1 Frank Kreith
atau tabel 4.1 Frank P. Incropera.

12. Contoh soal :
Suatu pipa panjang penyalur crude-oil ditanam
dalam tanah sedalam 1.5 m. Diameter luar
pipa 0.5 m. Jika temperatur crude-oil rata-rata
120 0C. Dan tempertur permukaan tanah 00C.
Tentukan :
a. Faktor bentuk
b. Jumlah kalor yang keluar crude-oil persatuan
panjang jika k tanah = 0.05 W/m.K