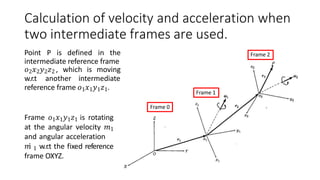
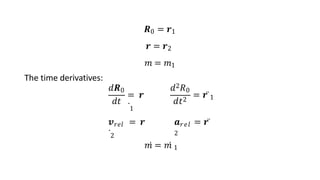
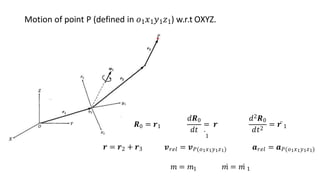
The document discusses the calculation of velocity and acceleration using two intermediate reference frames and provides case studies involving angular motions and corresponding transformations. It explores the dynamics of a bird on a rotating mobile structure and a robot manipulating a workpiece, detailing the velocities and accelerations involved at various points. The analysis is framed in terms of intermediate reference frames, detailing the motion relative to fixed and intermediate frames.

1. Generalizations of kinematic
expressions

2. Calculation of velocity and acceleration when
two intermediate frames are used.
Point P is defined in the
intermediate reference frame
𝑜2𝑥2𝑦2𝑧2 , which is moving
w.r.t another intermediate
reference frame 𝑜1𝑥1𝑦1𝑧1.
Frame 𝑜1𝑥1𝑦1𝑧1 is rotating
at the angular velocity 𝑚1
and angular acceleration
𝑚
˙ 1 w.r.t the fixed reference
frame OXYZ.
Frame 0
Frame 2
Frame 1

3. Case – 1
The angular motions of 𝑜2𝑥2𝑦2𝑧2, 𝑚2 and 𝑚˙2, are defined w.r.t frame
OXYZ.
Case – 2
The angular motions of 𝑜2𝑥2𝑦2𝑧2, 𝑚2 and 𝑚˙2, are defined w.r.t frame
𝑜1𝑥1𝑦1𝑧1.

4. Case 1:
The angular motions of 𝑜2𝑥2𝑦2𝑧2, 𝑚2 and 𝑚˙2, are defined w.r.t frame
OXYZ.
Question:
Find the motion of P w.r.t OXYZ.
Solution:
Find the motion of 𝑜2 w.r.t OXYZ and then the motion of P w.r.t OXYZ.

5. Motion of 𝑜2 (defined in 𝑜1𝑥1𝑦1𝑧1) w.r.t OXYZ.
𝑑
𝑡
𝑟𝑒
𝑙
Velocity of P: 𝒗 = 𝑑𝑹0
+ 𝒗 + 𝑚 × 𝒓
𝑑𝑡2
2
Acceleration of P: 𝒂 = 𝑑 𝑹0
+ 𝒂𝑟𝑒
𝑙
+ 2𝑚 × 𝒗𝑟𝑒
𝑙
+ 𝑚˙× 𝒓 + 𝑚 × 𝑚 × 𝒓

6. 𝑹0 = 𝒓1
𝒓 = 𝒓2
𝑚 = 𝑚1
The time derivatives:
𝑑𝑹0
𝑑𝑡
= 𝒓
˙1
𝑑2𝑅0
𝑑𝑡2
= 𝒓¨1
𝒗𝑟𝑒𝑙 = 𝒓
˙2
𝒂𝑟𝑒𝑙 = 𝒓¨
2
𝑚
˙ = 𝑚
˙ 1

7. 𝒗𝑜2(𝑂𝑋𝑌𝑍)
𝑑𝑡 𝑟𝑒
𝑙
𝑑𝑹0
= + 𝒗 + 𝑚 × 𝒓
= 𝒓˙1 + 𝒓˙2 + 𝑚1 ×
𝒓2
𝒂𝑜2 𝑂𝑋𝑌𝑍 =
𝑑2𝑹0
𝑑𝑡2
+ 𝒂𝑟𝑒𝑙 + 2𝑚 × 𝒗𝑟𝑒𝑙 + 𝑚˙× 𝒓 + 𝑚 × 𝑚 × 𝒓
= 𝒓¨1 + 𝒓¨2 + 2𝑚1 × 𝒓˙2 + 𝑚˙1 × 𝒓2 + 𝑚1 × 𝑚1
× 𝒓2
Velocity and acceleration of point 𝑜2 w.r.t OXYZ.

8. Motion of P (defined in 𝑜2𝑥2𝑦2𝑧2) w.r.t OXYZ.
𝑹0 = 𝒓1 + 𝒓2
𝑑𝑹0
= 𝒗
𝑑𝑡 𝑜2(𝑂𝑋𝑌𝑍)
𝑑2𝑹0
𝑑𝑡2
= 𝒂𝑜2(𝑂𝑋𝑌𝑍)
𝒓 = 𝒓3 𝒗𝑟𝑒𝑙 = 𝒓
˙3
𝒂𝑟𝑒𝑙 = 𝒓¨
3
𝑚 = 𝑚2 𝑚
˙ = 𝑚
˙ 2

9. 𝒗𝑃(𝑂𝑋𝑌𝑍
)
𝑑𝑡 𝑟𝑒
𝑙
𝑑𝑹0
= + 𝒗 + 𝑚 × 𝒓
= 𝒗𝑜2(𝑂𝑋𝑌𝑍) + 𝒓˙3 + 𝑚2 × 𝒓3
= 𝒓˙1 + 𝒓˙2 + 𝒓˙3 + 𝑚1 × 𝒓2 + 𝑚2 ×
𝒓
3
Velocity of point P w.r.t OXYZ.

10. 𝒂𝑃 𝑂𝑋𝑌𝑍 =
𝑑2𝑹0
𝑑𝑡2
+ 𝒂𝑟𝑒𝑙 + 2𝑚 × 𝒗𝑟𝑒𝑙 + 𝑚˙× 𝒓 + 𝑚 × 𝑚 × 𝒓
= 𝒂𝑜2(𝑂𝑋𝑌𝑍) + 𝒓¨3 + 2𝑚2 × 𝒓˙3 + 𝑚˙2 × 𝒓3 + 𝑚2 × 𝑚2 × 𝒓3
= 𝒓¨1 + 𝒓¨2 + 𝒓¨3 + 2𝑚1 × 𝒓˙2 + 2𝑚2 × 𝒓˙3 + 𝑚
˙ 1 × 𝒓2 + 𝑚
˙ 2 ×
𝒓
3+
𝑚1 × 𝑚1 × 𝒓2 + 𝑚2 × 𝑚2 × 𝒓3
Acceleration of point P w.r.t OXYZ.

11. Case – 2
The angular motions of 𝑜2𝑥2𝑦2𝑧2, 𝜔2 and 𝜔˙ 2, are defined w.r
.t frame
𝑜1𝑥1𝑦1𝑧1.
Question:
Find the motion of P w.r.t OXYZ.
Solution:
Find the motion of P w.r.t 𝑜1𝑥1𝑦1𝑧1 and then the motion of P w.r.t
OXYZ.

12. Motion of point P (defined in 𝑜2𝑥2𝑦2𝑧2) w.r.t 𝑜1𝑥1𝑦1𝑧1.
𝑹0 = 𝒓2
𝑑𝑹0
𝑑𝑡
= 𝒓
˙2
𝑑2𝑹0
𝑑𝑡2
= 𝒓¨2
𝒓 = 𝒓3 𝒗𝑟𝑒𝑙 = 𝒓˙
3
𝒂𝑟𝑒𝑙 = 𝒓¨
3
𝑚 = 𝑚2 𝑚
˙ = 𝑚
˙ 2
𝒗𝑃(𝑜1𝑥1𝑦1𝑧1) = 𝒓˙2 + 𝒓˙3 + 𝑚2 ×
𝒓3
𝒂𝑃(𝑜1𝑥1𝑦1𝑧1) = 𝒓¨2 + 𝒓¨3 + 2𝑚2 × 𝒓˙3 + 𝑚˙2 × 𝒓3 + 𝑚2 × (𝑚2 × 𝒓
3
)

13. Motion of point P (defined in 𝑜1𝑥1𝑦1𝑧1) w.r.t OXYZ.
𝑹0 = 𝒓1
𝑑𝑹0
𝑑𝑡
= 𝒓
˙1
𝑑2𝑹0
𝑑𝑡2
= 𝒓¨1
𝒓 = 𝒓2 + 𝒓3 𝒗𝑟𝑒𝑙 = 𝒗𝑃(𝑜1𝑥1𝑦1𝑧1)
𝑚 = 𝑚1 𝑚
˙ = 𝑚
˙ 1
𝒂𝑟𝑒𝑙 = 𝒂𝑃(𝑜1𝑥1𝑦1𝑧1)

14. 𝒗𝑃(𝑂𝑋𝑌𝑍) = 𝒓˙1 + 𝒗𝑃(𝑜1𝑥1𝑦1𝑧1) + 𝑚1 ×
= 𝒓˙1 + 𝒓˙2 + 𝒓˙3 + 𝑚1 × 𝒓2 +
𝒓2 + 𝒓3
𝑚1 + 𝑚2 × 𝒓3
𝒓2 + 𝒓3 + 𝑚1
𝒂𝑃(𝑂𝑋𝑌𝑍)
= 𝒓¨1 + 𝒂𝑃(𝑜1𝑥1𝑦1𝑧1) + 2𝑚1 × 𝒗𝑃(𝑜1𝑥1𝑦1𝑧1) + 𝑚
˙
1
× 𝑚1 × 𝒓2 + 𝒓3
= 𝒓¨1 + 𝒓¨2 + 𝒓¨3 + 2𝑚1 × 𝒓˙2 + 2 𝑚1 + 𝑚2 × 𝒓3̇ +
𝑚
˙ 1 × 𝒓2
+ 𝑚˙1 + 𝑚˙2 × 𝒓3 + 𝑚2 × 𝑚2 × 𝒓3 + 2𝑚1 × (𝑚2 × 𝒓3) + 𝑚1
× 𝑚1 × 𝒓𝟐 + 𝒓3

15. Bird on mobile.
An artistic mobile structure is modeled as sketched in Figure 1(a), consists of
a large + and four smaller Y’s, one each attached to a tip of the +. The + is
horizontal at all times and rotates at a constant angular velocity 𝜔1 (w.r.t
ground) about an axis through its center. Also, each four Y’s remains at all
times in a vertical plane and rotates at a constant angular velocity 𝜔2 (w.r.t
its + tip) about an axis through its center. At the instant shown, a bird of
mass 𝑚 is on a leg of one of the Y’s, which is oriented as indicated in Figure
1(b). Relative to the Y, the bird is running with a velocity 𝑣0 and an
acceleration 𝑎0, at the instant shown. At the same instant, a gust of wind
exerts a force 𝐹𝑤 on the bird in the X direction.
Find the velocity and acceleration of the bird, which may be modeled as a
point, at the instant shown.

16. Figure 1(a): Mobile structure Figure 1(b): Detail of Y and bird.
Figure 1: Sketch of artistic mobile structure with bird running along
horizontal leg of Y.

17. 1. Motion of bird (defined in 𝑜2𝑥2𝑦2𝑧2) w.r.t 𝑜1𝑥1𝑦1𝑧1.
2. Motion of bird (defined in 𝑜1𝑥1𝑦1𝑧1) w.r.t OXYZ.

18. Robot manipulating work piece.
A robot named JT is rolling w.r.t the shop floor at a constant speed of
0.5 m/s and carrying a work piece 1 m long, as sketched in Figure 2.
each of the links of the robot arm is 0.75 m long, and the second link
has an end gripper that holds the work piece which ,ay be considered
as rigid. At the instant shown, the link AB is rotating a 𝜔1 (1 rev/3 s),
and link BD is rotating at 𝜔2 (1 rev/2 s) and 𝜔˙2 (0.5 rad/s2), all w.r.t the
shop floor.
At the instant shown, find the velocity and acceleration of the center of
the work piece, labeled point C, as sketched in Figure 2.

19. Figure 2: JT manipulating work piece.

20. 1. Using the frame 𝐴𝑥1𝑦1𝑧1 as an intermediate frame, find the motion
of point B w.r.t the fixed reference frame 𝑂𝑋𝑌𝑍.
2. Using the frame 𝐵𝑥2𝑦2𝑧2 as an intermediate frame, find the motion
of point C w.r.t the fixed reference frame 𝑂𝑋𝑌𝑍.