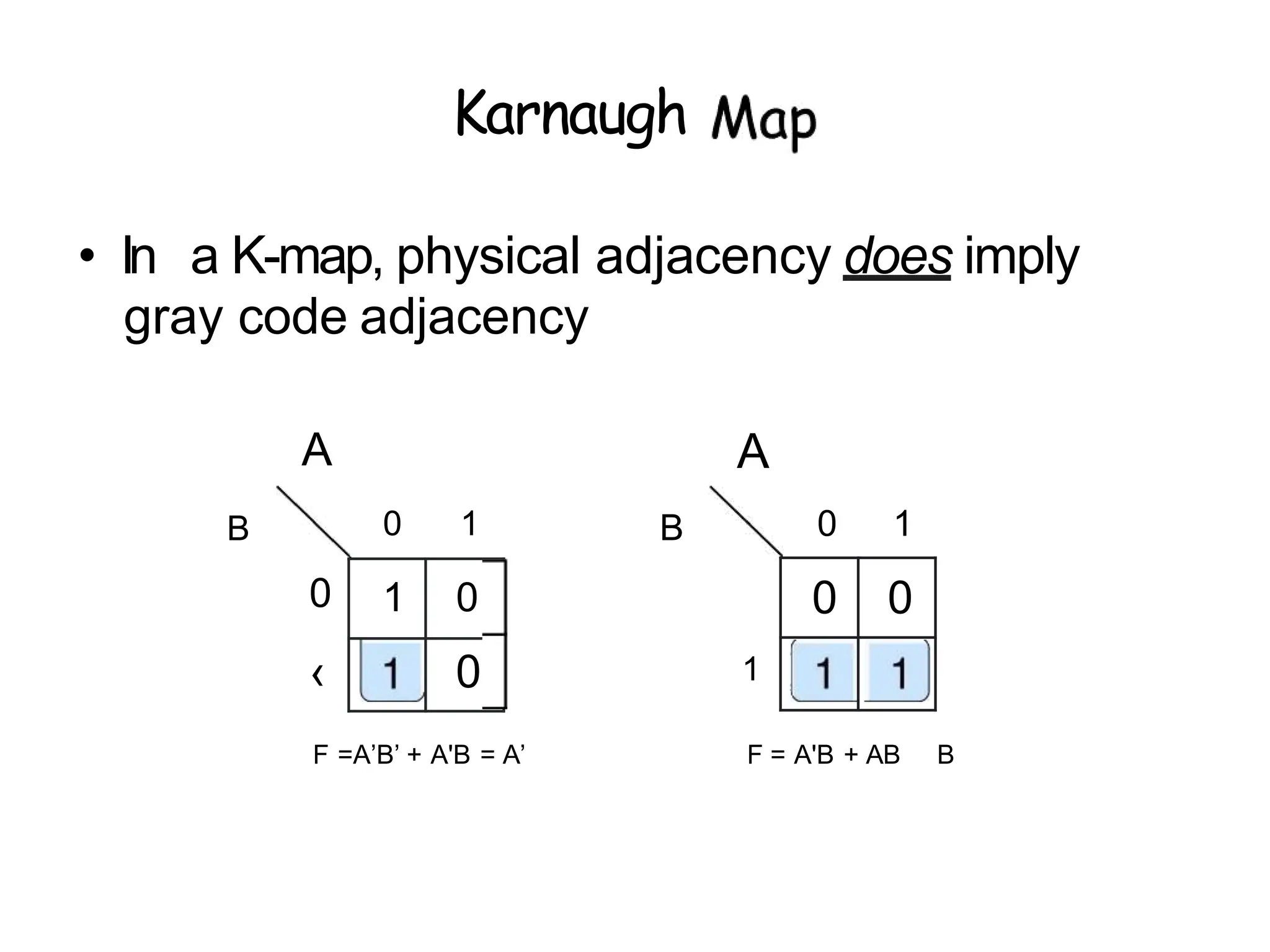
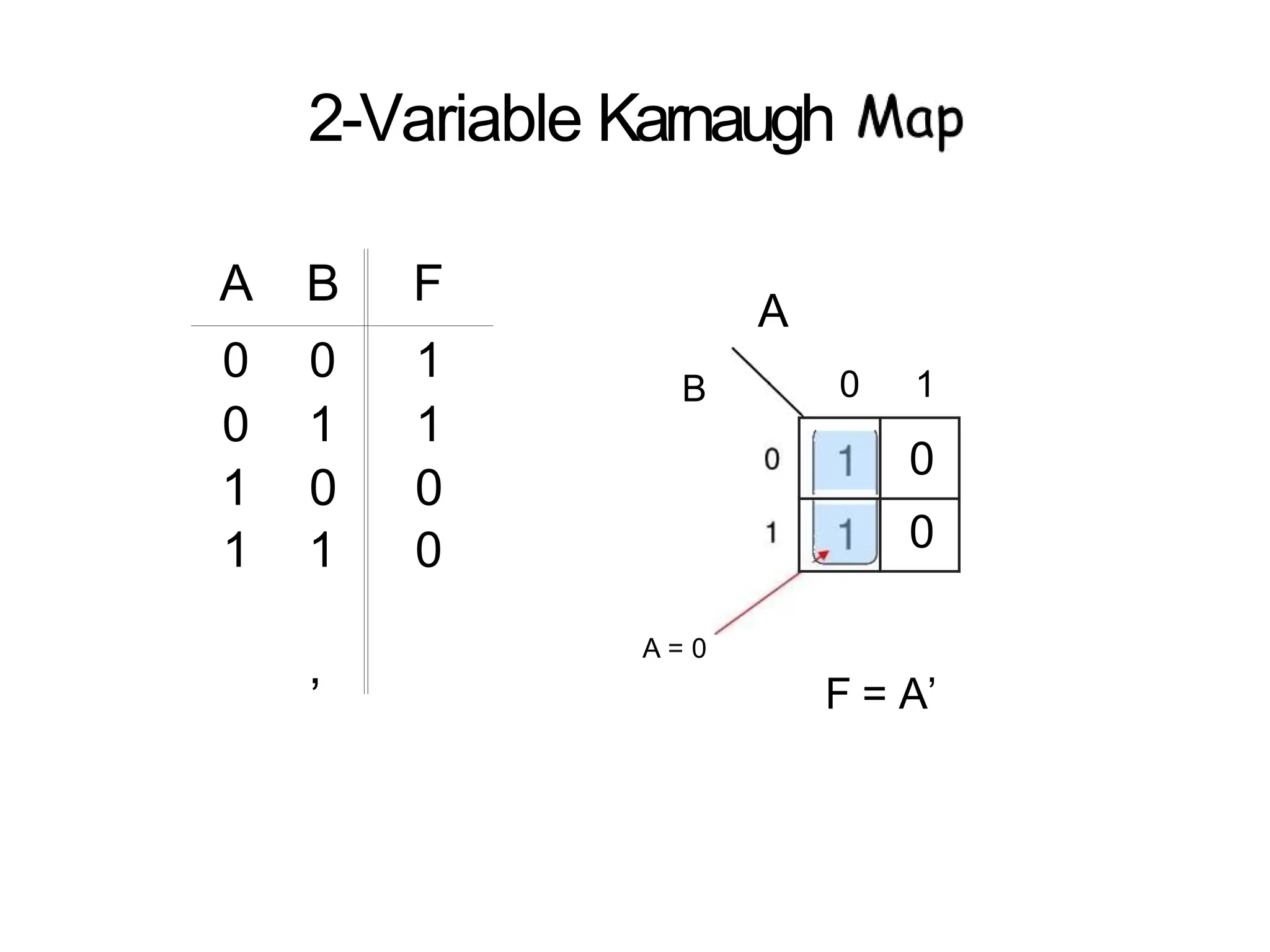
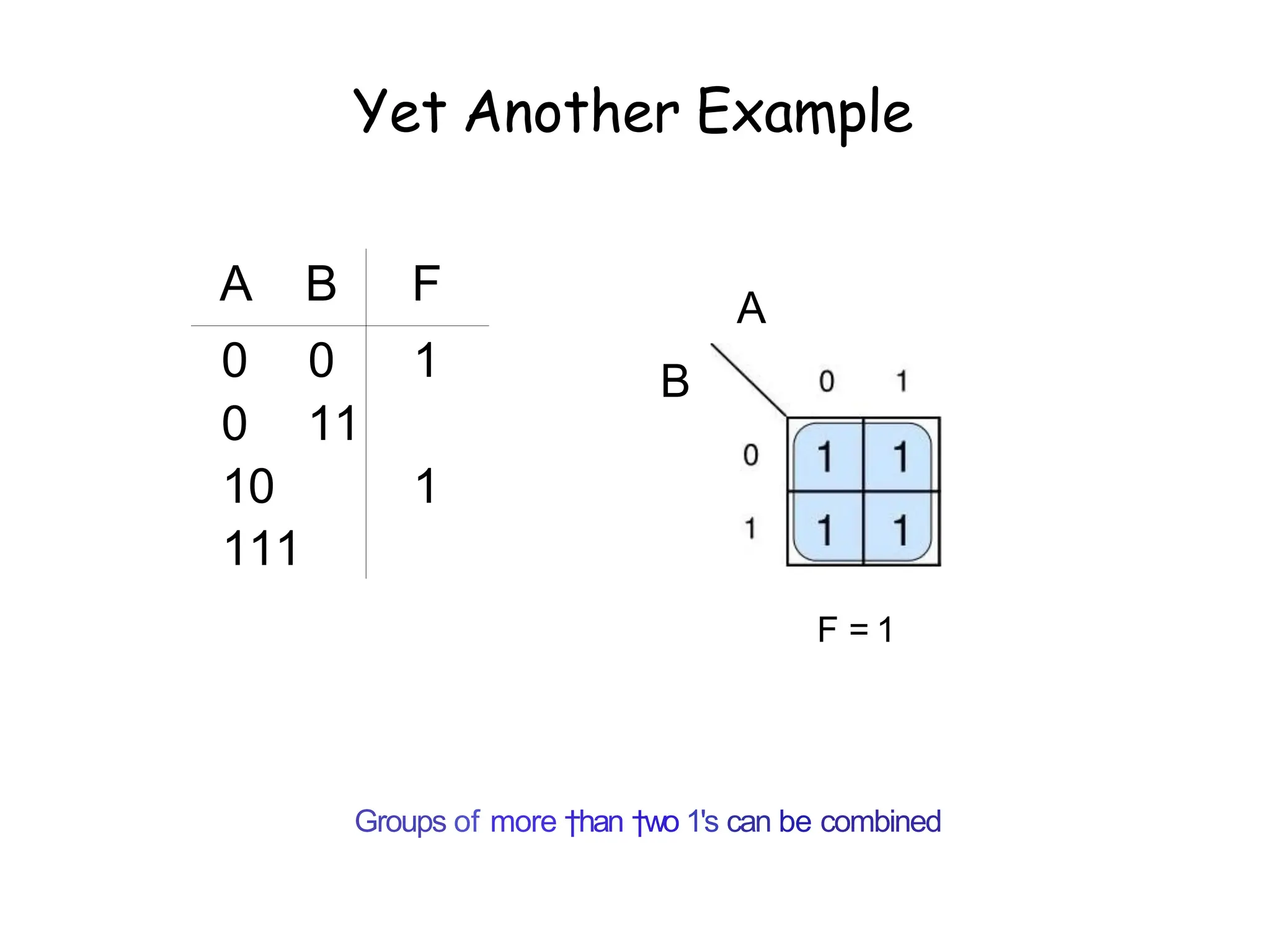
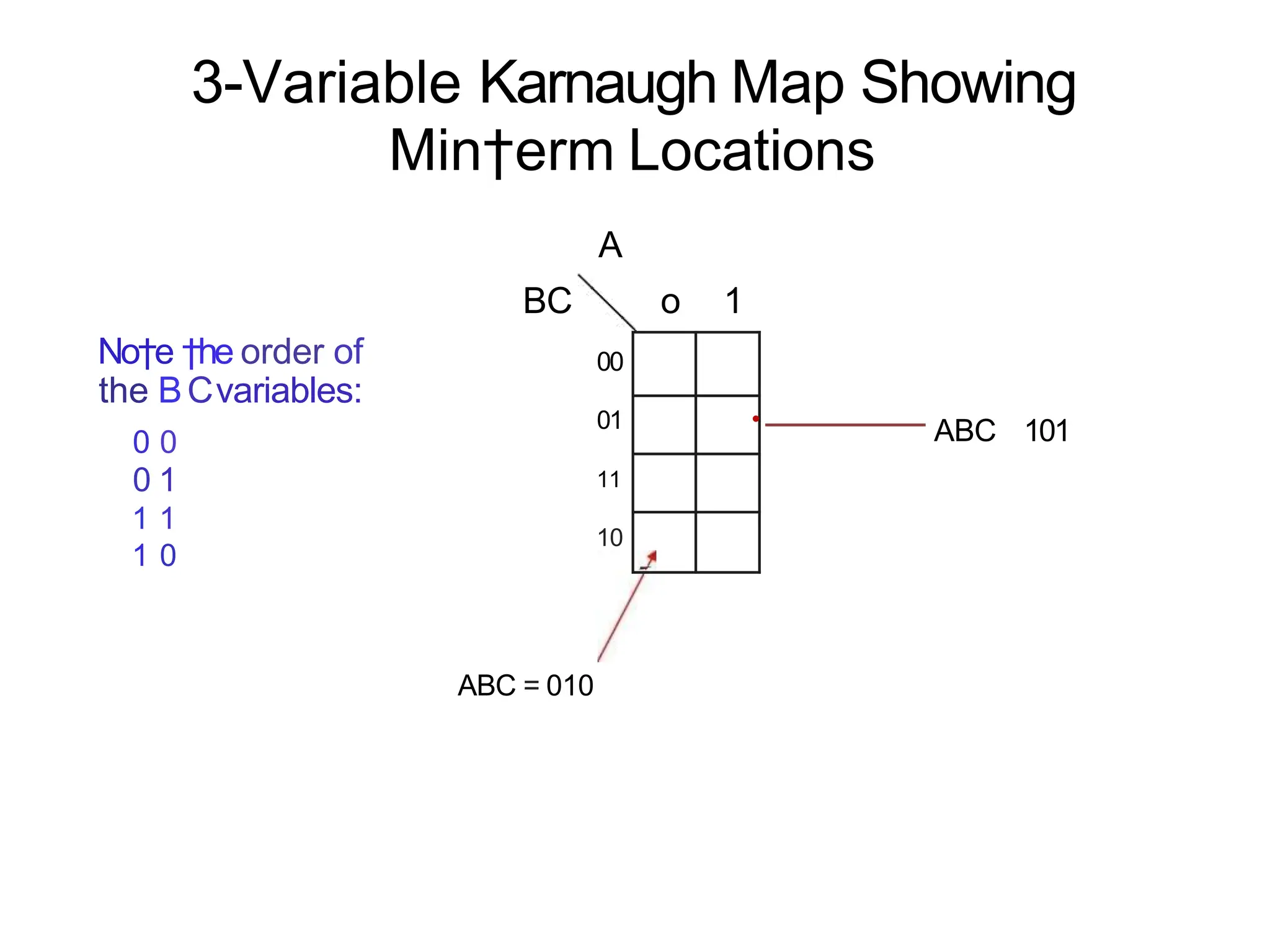
Karnaugh maps offer a systematic method for minimizing logic functions through graphical representation, simplifying the process compared to Boolean minimization. The document explains the adjacency in Gray code and how it applies to Karnaugh maps, emphasizing that physical adjacency in the map indicates Gray code adjacency. Various examples illustrate the application of Karnaugh maps for simplification of multi-variable logic functions.

1. Karnaugh

2. What are Karnaugh Maps?
A simpler way †o handle mos† (bu† no†
all) jobs of mani ula†in logic functions.

3. Karcaugh Advantages
• Minimization can be done more sys†ema†ically
• Much simpler †o find minimum solutions
• Easier †o see wha† is happening (graphical)
Almost always used instead
of boolean minimization.

4. 2-bi† Gray
Code
00
01
11
10
Gray Codes
• Gray code is a binary value encoding in which
adjacen† values only differ by one bi†

5. F = A’
F=B
Key idea:
Gray code adjacency allows use of
simplification theorems
A B
0 0
O 0
Truth Table Adjacencies
These are adjacent in a9naycode sense -
†hey differ by 1bi†
We can apply XY + XY’ = X
A'B’ + A'B = A’(B'+B) A’(1) = A
Some idea:
A'B + AB = B
Problem:
Physical adjacency in †ruth †abIe does
not indicate gray code adjacency

6. 2-Variable Karnaugh
A-0, B—0
A-0, B-1
A=1, B=0
A-1, B-1
A differen† way †o draw a †ru†h †abIe: by folding i†

7. A
0 1
0 1 0
‹ 0
0 0
Karnaugh
• In a K-map, physical adjacency does imply
gray code adjacency
A
B
F =A’B’ + A'B = A’
B 0 1
1
F = A'B + AB B

8. A B F
0 0 1
0 1 1
1 0 0
1 1 0
2-Variable Karnaugh

9. A B F
0 0 1
0 1 1
1 0 0
1 1
,
0
2-Variable Karnaugh
A
B 0 1
0

10. A B F
0 0 1
0 1 1
1 0 0
1 1
,
0
2-Variable Karnaugh
A
0 1
1
1

11. A B F
0 0 1
0 1 1
1 0 0
1 1
,
0
- 0
*0
2-Variable Karnaugh
A
B 0 1

12. A B F
0 0 1
0 1 1
1 0 0
1 1
,
0
2-Variable Karnaugh
A
B 0 1
1 0
1 0
0
1
F = A'B’ + A'B = A’

13. A B F
0 0 1
0 1 1
1 0 0
1 1
,
0
0
0
2-Variable Karnaugh
A
B 0 1
A = 0
F = A’

14. A B F
0 0 0
0 1 1
1 0 1
1 1 1
Another Example
A
B 0 1
0 1
1
0
1
F = A'B + AB’ + AB
(A'B + AB) + (AB’ + AB)
= A+ B
1

15. A B F
0 0 0
0 1 1
1 0 1
1 1 1
Another Example
B = 1
F = A + B
A
A = 1

16. A B F
0 0 1
0 11
10 1
111
Yet Another Example
A
B
F = 1
Groups of more †han †wo 1's can be combined

17. •
3-Variable Karnaugh Map Showing
Min†erm Locations
A
BC o 1
No†e †he order of
the BCvariables:
0 0
0 1
1 1
1 0
ABC = 010
00
01
11
10
ABC 101