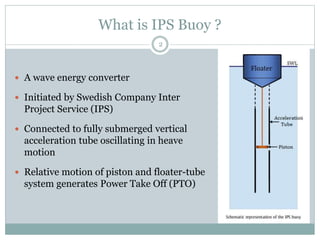
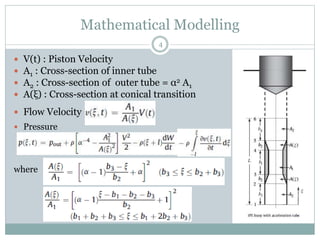
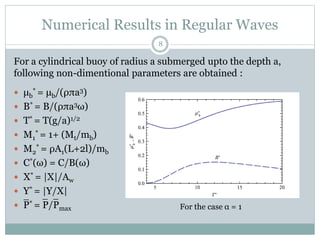
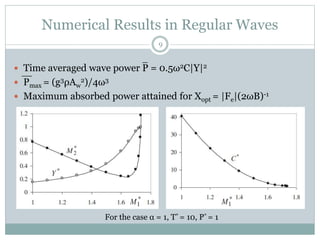
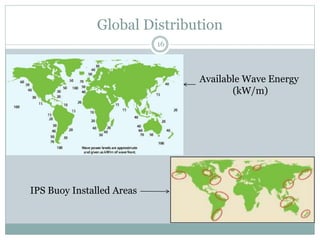
This document describes the hydrodynamic analysis of the IPS Buoy wave energy converter including the effect of non-uniform acceleration tube cross-section. The IPS Buoy system uses the relative motion between a submerged vertical acceleration tube and a piston inside the tube to generate power as they oscillate in heave motion due to incoming waves. The analysis involves developing mathematical models of the system and its components under assumptions like one-dimensional flow inside the tube. Numerical results are presented for the power absorbed and other parameters in regular and irregular wave conditions.

1. HY D R O D Y N A M I C S OF TH E IPS BU O Y WA V E EN E R G Y CO N V E R T E R
IN C L U D I N G TH E EF F E C T OF NO N -UN I F O R M AC C E L E R A T I O N TU B E
CR O S S SE C T I O N
A N T Ó N I O F . O . F A L C Ã O
J O S É J . C Â N D I D O
P A U L O A . P . J U S T I N O
J O Ã O C . C . H E N R I Q U E S
IPS Buoy
Abhishek Mondal
IIT Kharagpur
IDMEC, Instituto Superior Técnico, Technical University of Lisbon, 1049-001 Lisbon, Portugal
Laboratório Nacional de Energia e Geologia, Estrada Paço do Lumiar, 1649-038 Lisbon, Portugal
1

2. What is IPS Buoy ?
 A wave energy converter
 Initiated by Swedish Company Inter
Project Service (IPS)
 Connected to fully submerged vertical
acceleration tube oscillating in heave
motion
 Relative motion of piston and floater-tube
system generates Power Take Off (PTO)
2

3. Assumptions
The buoy-tube-piston system is mathematically modelled using the
following assumptions :
 Buoy-tube system has heave motion only
 The tube is sufficiently below the water surface; thus the
excitation & radiation force become negligible.
 Negligible interaction between the wave fields at tube ends
 Flow inside the tube is one dimensional
 Piston has negligible length and mass
3

4. Mathematical Modelling
 V(t) : Piston Velocity
 A1 : Cross-section of inner tube
 A2 : Cross-section of outer tube = α2 A1
 A(ξ) : Cross-section at conical transition
 Flow Velocity
 Pressure
where
4

5. Hydrodynamic Analysis in Regular Waves
 Force on piston:
fp(t)= -Mxx - Myy+Ky+Cy

 Power absorbed by PTO
P = fp(t)y
 Wave excitation force
fe(t) = AwΓ(ω)eiωt
 Force on the tube
ft(t) = -mxx - myy
• x(t): floater-tube position
• y(t): position of piston
• K : spring stiffness
• C : PTO damping coeff.
• Aw: linear wave amplitude
• ω: wave frequency
• Mb: buoy mass (mb) +
added mass (μb)
• Mt: tube mass (mt) +
added mass (μt)
• Γ(ω): excitation force coeff.
• β : half-angle
• l : added length
5

6. Hydrodynamic Analysis in Regular Waves
6
Where
Mx = ρA1(L+2l)
My = ρA1(b1+α-2(b3+b4+2l)+2b2α-1)
mx = ρA1[0.667b2(α2+α-2) + (α2 -1)(b3+b4+2l)]
my = ρA1[2b2(1 - α-1) + (1 – α-2)
 Equation of motion :
 {x(t), y(t), fe(t)} = {X, Y, Fe}eiωt
(Mb+Mt)x + Bx + ρgSx = fe(t) + ft(t) + fp(t)

7. Hydrodynamic Analysis in Regular Waves
7
Solving governing equation of motion of the system under the
influence of linear sinusoidal wave field :
-ω2(Mb+Mt+mx+Mx)X + iωBX + ρgSX - ω2(my+My)Y = Fe --> (1)
-ω2MxX - ω2MyY + (K+iωC)Y = 0 --> (2)
Linear algebraic equations (1) & (2) is further solved to find
X & Y and thus x(t) and y(t) are obtained

8. Numerical Results in Regular Waves
For a cylindrical buoy of radius a submerged upto the depth a,
following non-dimentional parameters are obtained :
 μb
* = μb/(ρπa3)
 B* = B/(ρπa3ω)
 T* = T(g/a)1/2
 M1
* = 1+ (Mt/mb)
 M2
* = ρA1(L+2l)/mb
 C*(ω) = C/B(ω)
 X* = |X|/Aw
 Y* = |Y/X|
 P* = P/Pmax
8
For the case α = 1
_ _ _

9. Numerical Results in Regular Waves
 Time averaged wave power P = 0.5ω2C|Y|2
 Pmax = (g3ρAw
2)/4ω3
 Maximum absorbed power attained for Xopt = |Fe|(2ωB)-1
9
For the case α = 1, T* = 10, P* = 1
_
__

10. T* = 12 T* = 14
10
Numerical Results in Regular Waves
α = 1

11. Comparison : α=1 & α=1.25
11
α =1
(black dots)
α =1.25
(white dots)
L*=L/a
b1
*= b1/a
=0.533
β =30o
T*=10
P*=1

12. Comparison : T*=10 & T*=12
12
T*=10
(white)
T*=12
(black)
b1
*= (b1/a) = 0.2
β =30o
P*=1
α = 4
_

13. Numerical Analysis in Irregular Waves
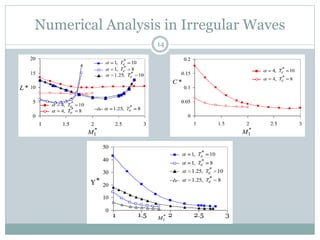
 Pierson-Moskowitz spectral distribution :
S(ω) = 526Hs
2 Te
-4 ω-5 exp(-1054 Te
-4 ω-4 )
[ Hs : Significant wave height ; Te: Energy period ]
 Time averaged power in irregular wave :
Pirr(Hs , Te) = ∫ Preg(ω) S(ω) dω
Pirr,max = 149.5 Hs
2 Te
3
 Non-dimensionalized parameters :
Te
* = Te (g/a)1/2 ; Pirr
* = Pirr/Pirr,max ; D2
* = D2/a
13
0
__
__
__
S(ω) = 526Hs
2 Te
-4 ω-5 exp(-1054 Te
-4 ω-4 )

14. Numerical Analysis in Irregular Waves
14

15. Key Benefits of IPS Buoy
15
 Renewable energy source
 Produces electricity for desalination
plants and remote areas
 Cluster of buoys act as wave breaker
 Easily expandable by adding more units
 Easy installation and maintenance
 Low production cost/kWh
 50-100 MW annual power generation
 Measures weather parameters and
forecast

16. Global Distribution
16
Available Wave Energy
(kW/m)
IPS Buoy Installed Areas

17. References
17
 Falcão AF de O. Wave energy utilization: a review of the technologies. Renew
Sust Energy Rev 2010; 14:899-918.
 Masuda Y. Wave-activated generator. Int. colloq. exposition oceans, Bordeaux,
France; 1971.
 Noren SA. Apparatus for recovering the kinetic energy of sea waves. US Patent
No. 4,773,221; 1988 [original Swedish Patent No. 8104407; 1981].
 Salter SH, Lin CP. Wide tank efficiency measurements on a model of the sloped
IPS buoy. In: Proc. 3rd European wave energy conf., Patras, Greece; 1998. p.
200-6.
 Evans DV. The oscillating water column wave-energy device. J Inst Math Appl
1978;22:423-33.
 Munson BR, Young DF, Okiishi TH. Fundamentals of fluid mechanics. 2nd ed.
New York: Wiley; 1994
 Falnes J. Optimum control of oscillation of wave-energy converters. Int J
Offshore Polar Eng 2002;12:147-55.

18. FOR
YOUR
ATTENTION
18
THANKS