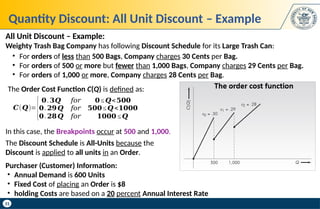
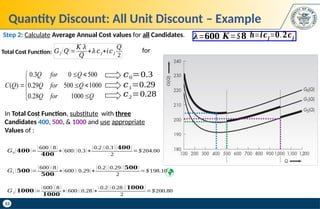
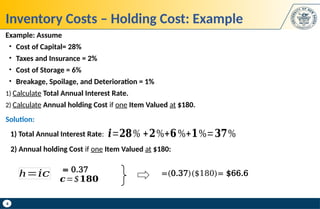
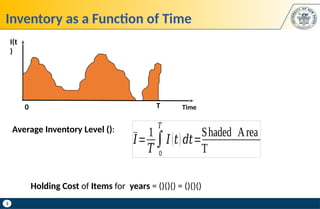
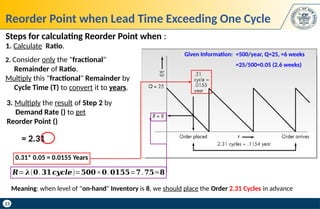
The document discusses key concepts in supply chain management, focusing on inventory management, including carrying costs, ordering costs, shortage costs, and the Economic Order Quantity (EOQ) model. It elaborates on the components of inventory costs, methods to calculate them, and the assumptions and formulas related to the EOQ model. Additionally, the document provides examples to illustrate the calculations associated with holding costs, ordering costs, and reorder points.














![26
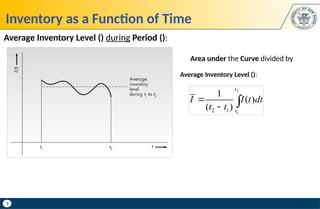
Sensitivity of Cost to Order Quantity Q: Tells us if we order Q instead of Q*, how much it
will affect Annual Cost (i.e., how much more it costs).
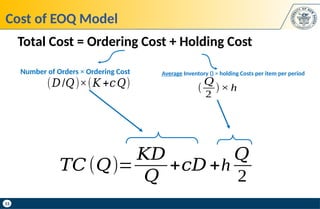
𝑇𝐶(𝑄)
𝑇𝐶(𝑄∗
)
=¿
𝐾 𝜆
𝑄
+
h𝑄
2
√2 𝐾 𝜆h
¿
1
2𝑄√2𝐾 𝜆
h
+
𝑄
2 √ h
2𝐾 𝜆
=
𝑄
∗
2𝑄
+
𝑄
2𝑄
∗
=
1
2[𝑄
∗
𝑄
+
𝑄
𝑄
∗ ]
Sensitivity of EOQ Model to Order Quantity Q
𝑇𝐶(𝑄)
𝑇𝐶(𝑄
∗
)
=
1
2 [𝑄
∗
𝑄
+
𝑄
𝑄
∗ ]
If we order Q: 𝑇𝐶(𝑄)=
𝐾 𝜆
𝑄
+
h𝑄
2
If we order Q*: 𝑇𝐶(𝑄∗
)=√2𝐾 𝜆h](https://image.slidesharecdn.com/inventorymanagementil-250203195907-c1ee7eea/85/Inventory-Management-Il-NETWORK-DESIGN-pptx-26-320.jpg)
![27
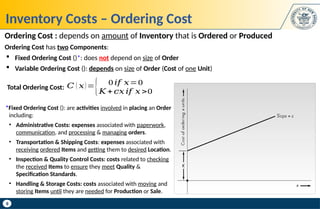
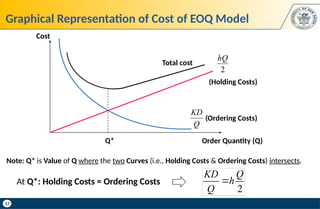
Example: Given an actual size of as twice the size of , how much it will affect
Annual Cost (how much more does it cost)?
Actual size of is twice the size of : 𝑸=𝟐𝑸∗
Interpretation:
The Error made in calculating Annual Cost (i.e., holding and Ordering Costs) as
a result of ordering wrong Value is: 0.25 * 100 = 25%
Meaning: If we order twice as the size of , Annual Cost increases by 25%
Sensitivity of EOQ Model to Order Quantity Q – Example
Solution:
¿
1
2 [1
2
+
2
1 ]
¿
1
2
[2.5]=𝟏.𝟐𝟓
1
2 [ 𝑄
∗
2𝑄
∗
+
2𝑄
∗
𝑄
∗ ]
¿ ¿
𝑸=𝟐𝑸∗
𝑇𝐶(𝑄)
𝑇𝐶(𝑄
∗
)
=
1
2 [𝑄
∗
𝑄
+
𝑄
𝑄
∗ ]](https://image.slidesharecdn.com/inventorymanagementil-250203195907-c1ee7eea/85/Inventory-Management-Il-NETWORK-DESIGN-pptx-27-320.jpg)
![28
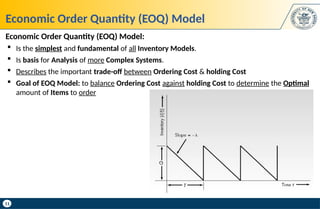
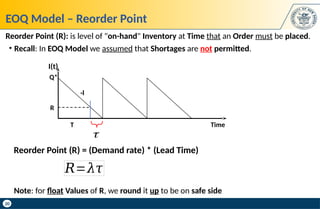
Sensitivity of Cost to Cycle Time T: Tells us how much different values of Time Cycles T (Order
Interval) will affect Annual Cost (i.e., how much more it costs).
Sensitivity of EOQ Model to Time Cycle T (Order Interval)
Annual Cost under 𝑇
Annual Cost under 𝑇
∗
=
𝑇𝐶(𝑇)
𝑇𝐶(𝑇
∗
)
=
1
2 [𝑇
∗
𝑇
+
𝑇
𝑇
∗ ]
𝑻 =
𝑸
𝝀
If we order Q: 𝑸=𝝀𝑻
𝑻
∗
=
𝑸∗
𝝀
If we order Q*: 𝑸∗
=𝝀𝑻∗
𝑇𝐶(𝑇 )
𝑇𝐶(𝑇
∗
)
=
1
2 [𝜆𝑇
∗
𝜆𝑇
+
𝜆𝑇
𝜆𝑇
∗ ]=
1
2 [𝑇
∗
𝑇
+
𝑇
𝑇
∗ ]
𝑇𝐶(𝑄)
𝑇𝐶(𝑄
∗
)
=
1
2 [𝑄
∗
𝑄
+
𝑄
𝑄
∗ ]
Sensitivity of EOQ Model to Order Quantity Q:
Sensitivity of EOQ Model to Time Cycle T:](https://image.slidesharecdn.com/inventorymanagementil-250203195907-c1ee7eea/85/Inventory-Management-Il-NETWORK-DESIGN-pptx-28-320.jpg)
![29
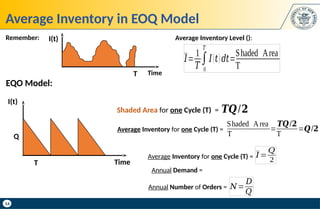
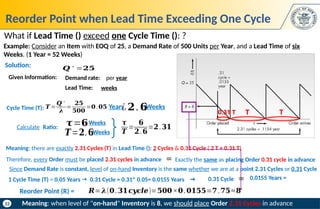
Example: Consider following information
Annual Cost under 𝑇
Annual Cost under 𝑇∗
=
𝑇𝐶(𝑇)
𝑇𝐶(𝑇∗
)
=
1
2 [𝑇
∗
𝑇
+
𝑇
𝑇∗ ]=
1
2 [0.154
0.169
+
0.169
0.154 ]=1.004
Annual Cost under 𝑇=$5916×1.004=$5939.664≈$5940
Now, suppose we have to round Time Cycle T to 8 Weeks. How much it will affect Annual Cost?
𝝀=𝟏𝟎𝟎𝟎
𝑸∗
=𝟏𝟔𝟗
𝑲=$𝟓𝟎𝟎
𝒉=𝟑𝟓
Sensitivity of EOQ Model to Time Cycle T (Order Interval) – Example
𝑻∗
=
𝑸∗
𝝀
=
𝟏𝟔𝟗
𝟏𝟎𝟎𝟎
=𝟎.𝟏𝟔𝟗𝒀𝒆𝒂𝒓𝒔=𝟖.𝟕𝟖𝟖𝑾𝒆𝒆𝒌𝒔
Optimal Time Cycle:
s
Solution:
$5940−$5916=$𝟐𝟒
Annual Cost increases by:
Annual Cost under
Interpretation: if we round Time Cycle T to 8 Weeks, Annual Cost increases by 0.4%](https://image.slidesharecdn.com/inventorymanagementil-250203195907-c1ee7eea/85/Inventory-Management-Il-NETWORK-DESIGN-pptx-29-320.jpg)