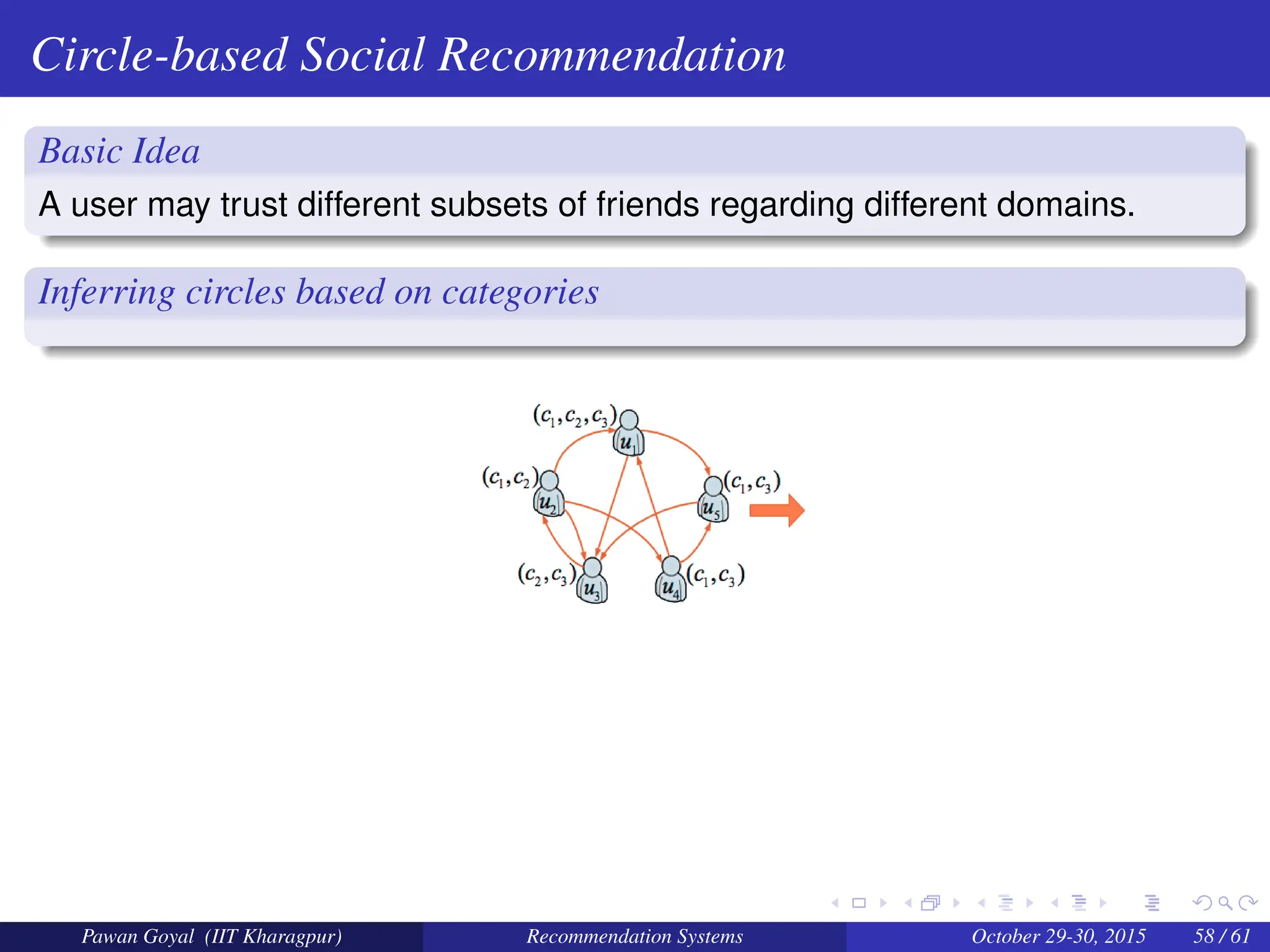
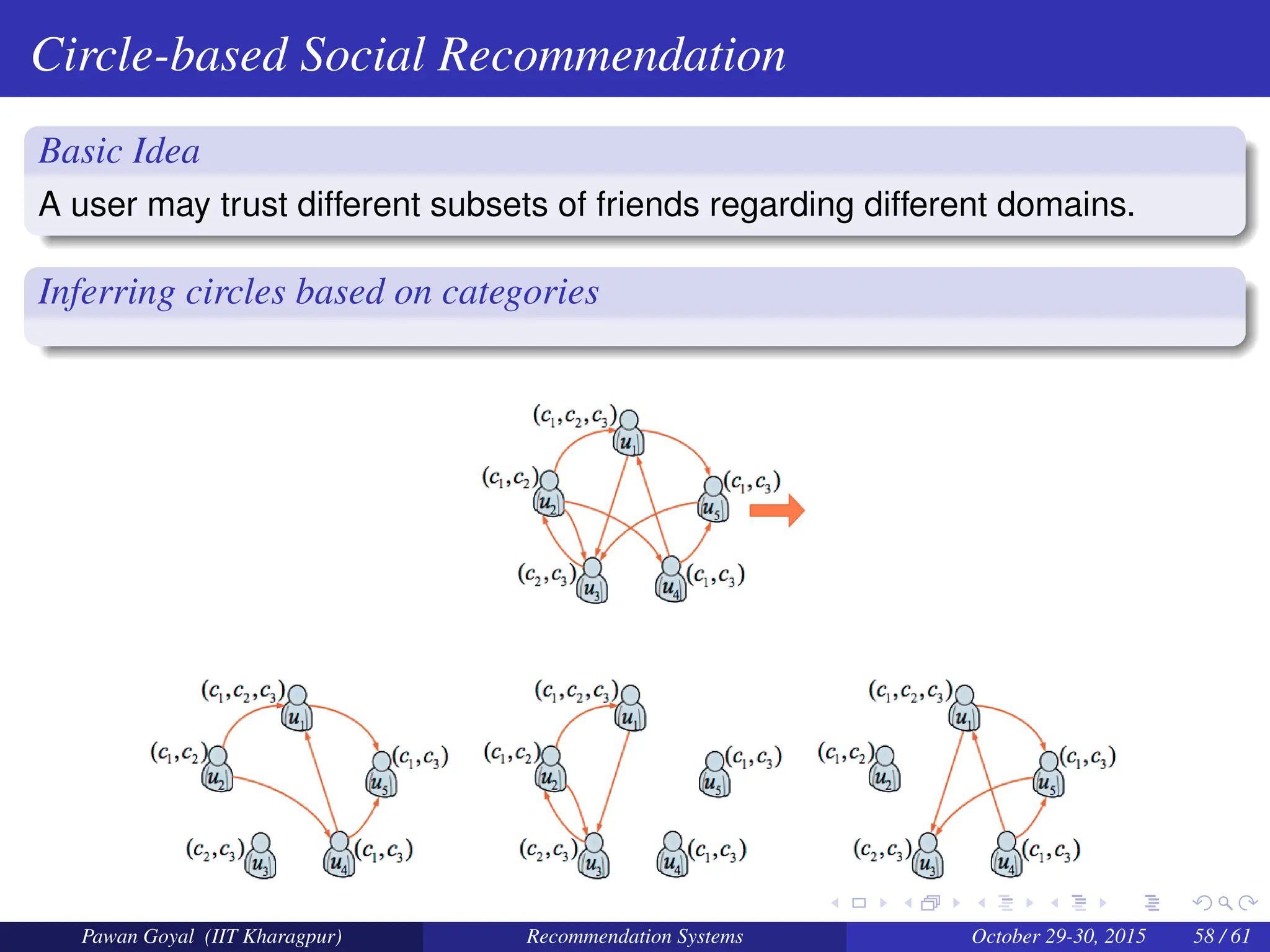
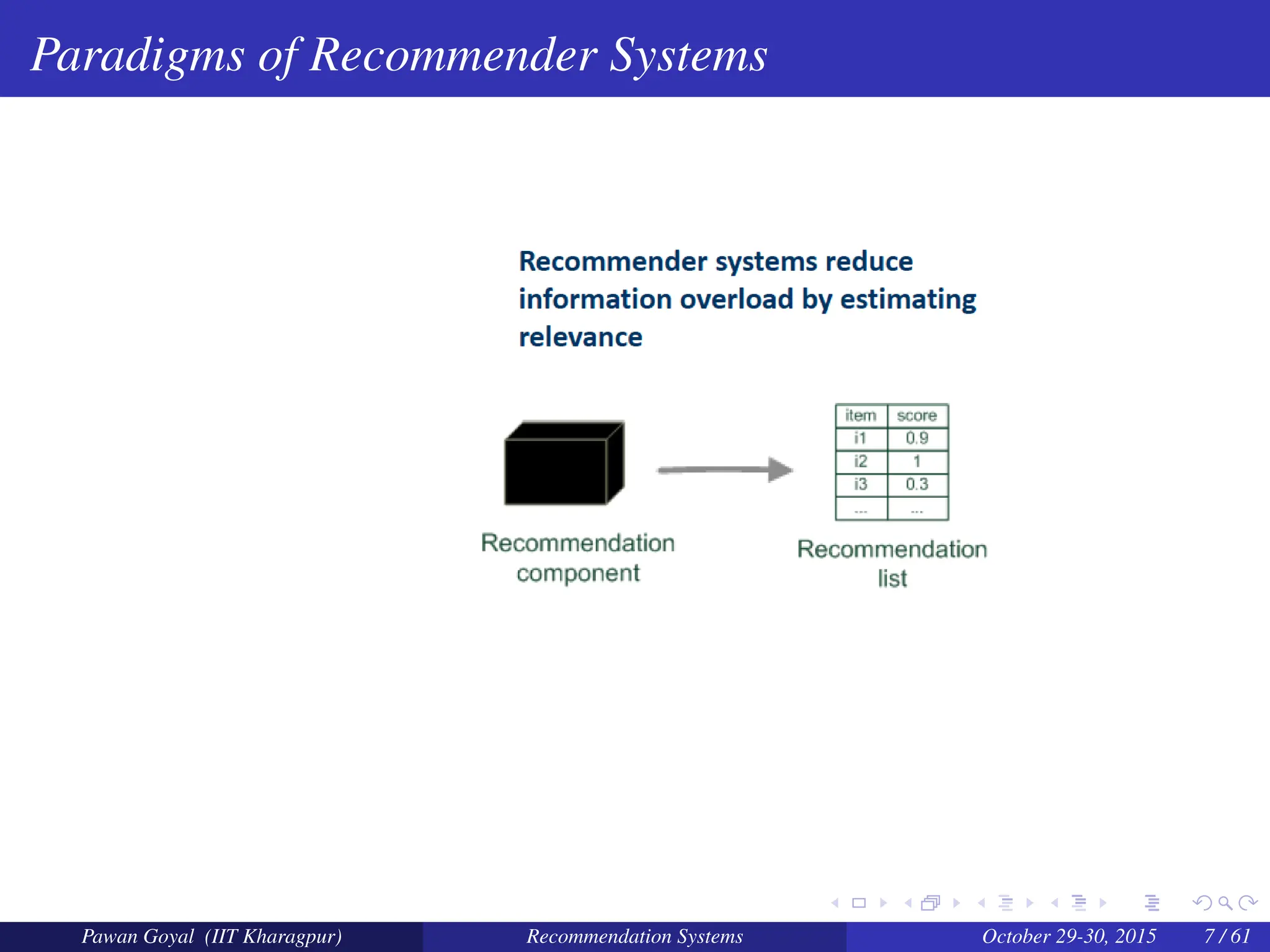
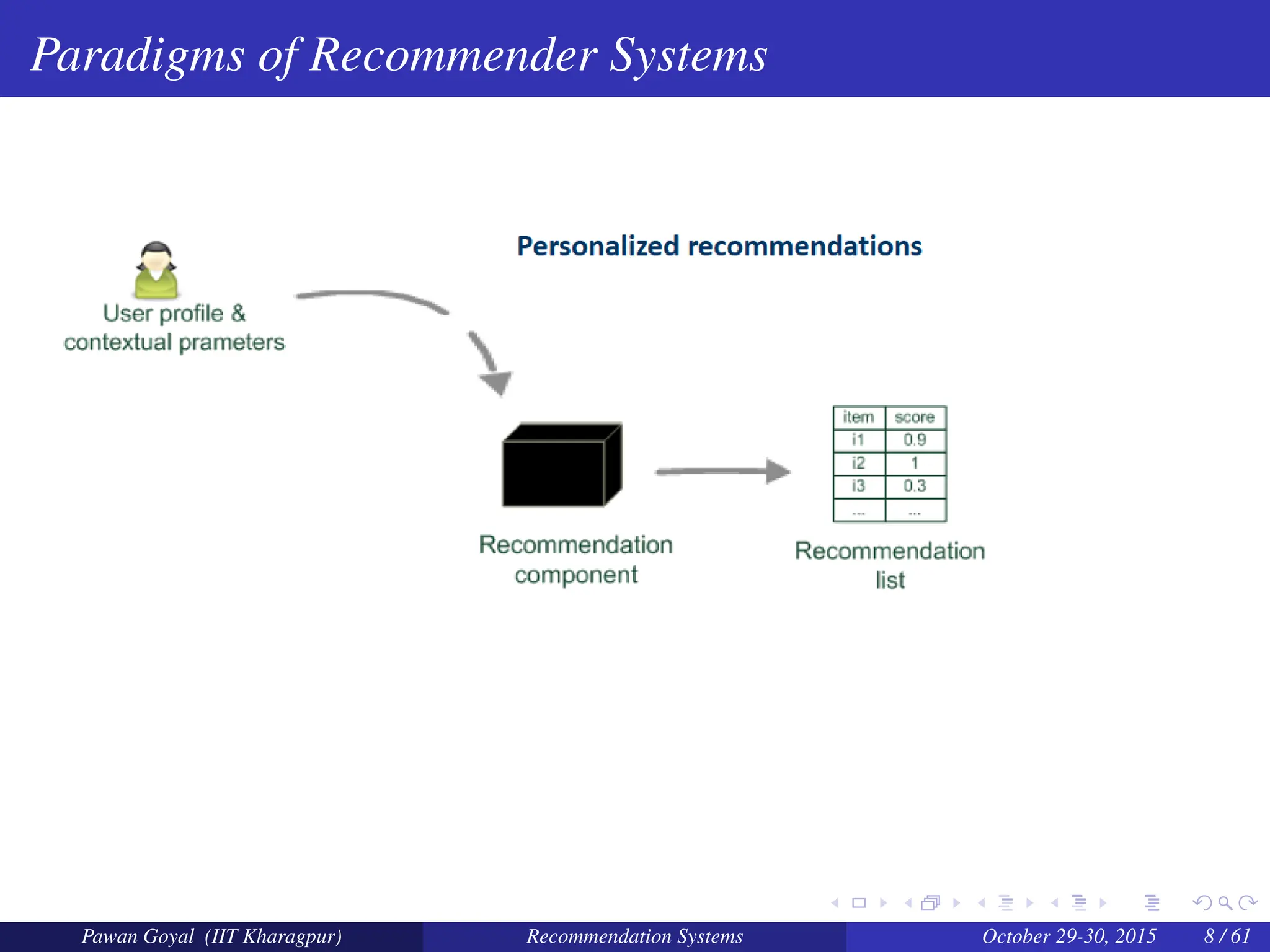
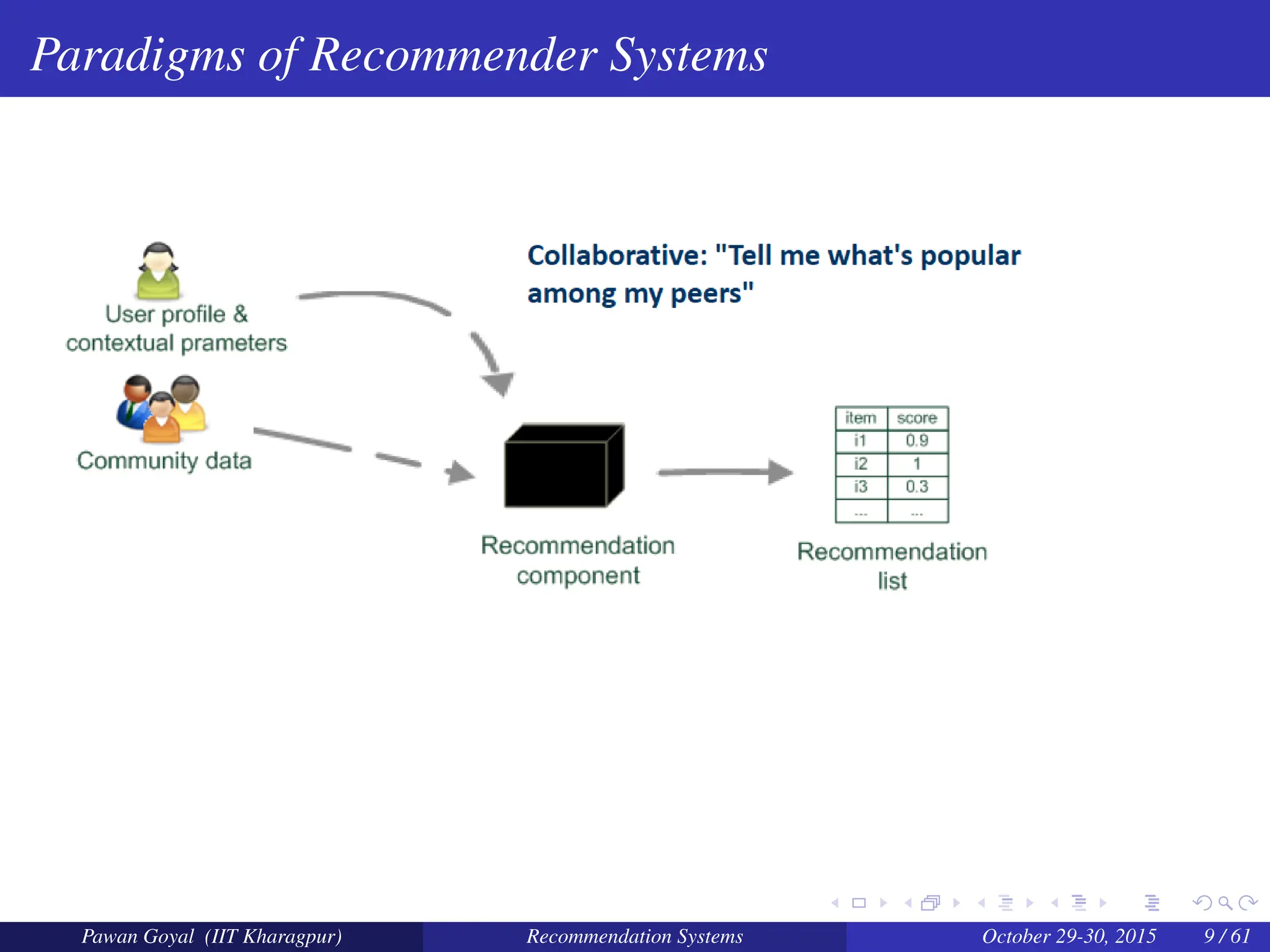
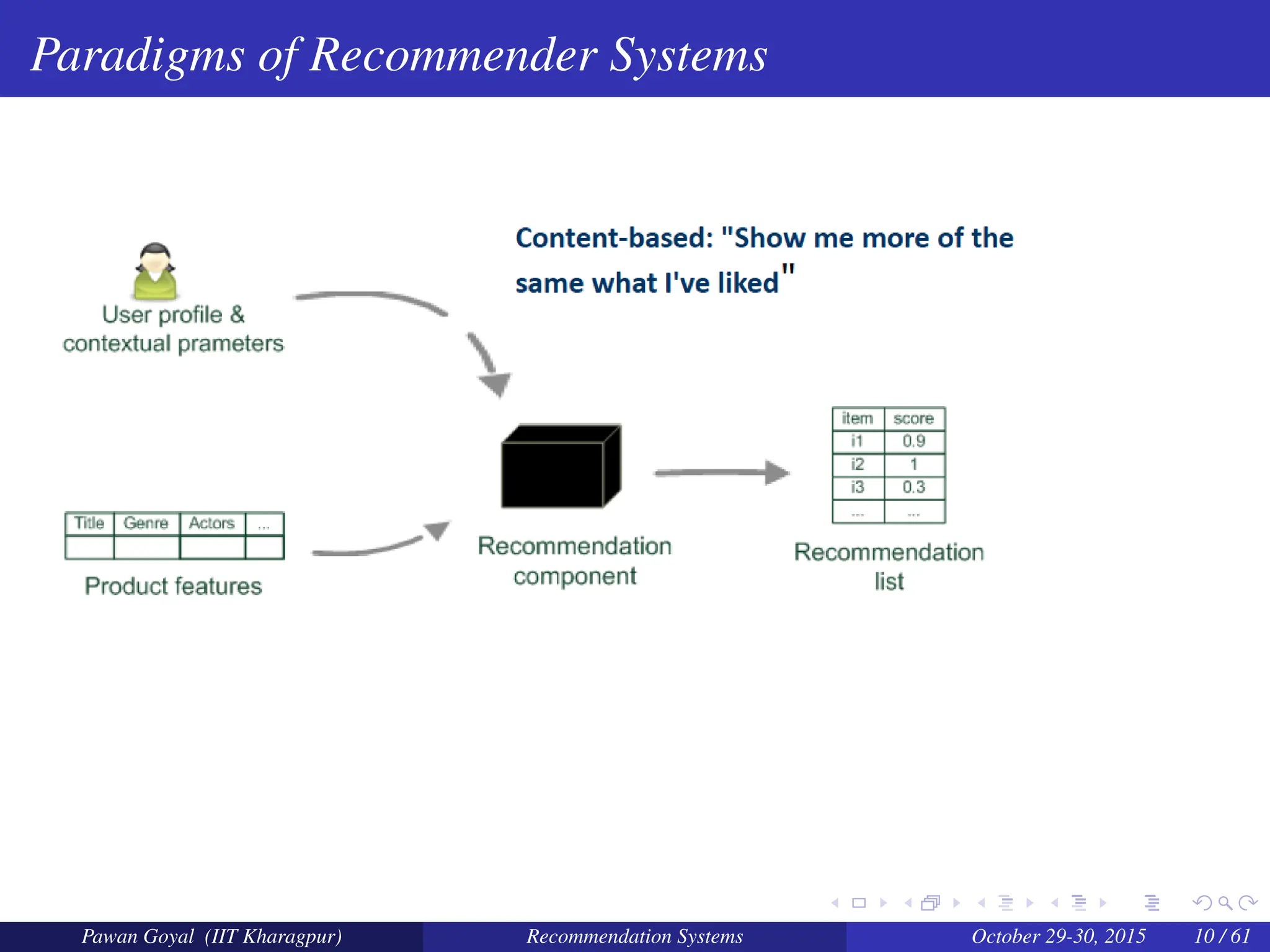
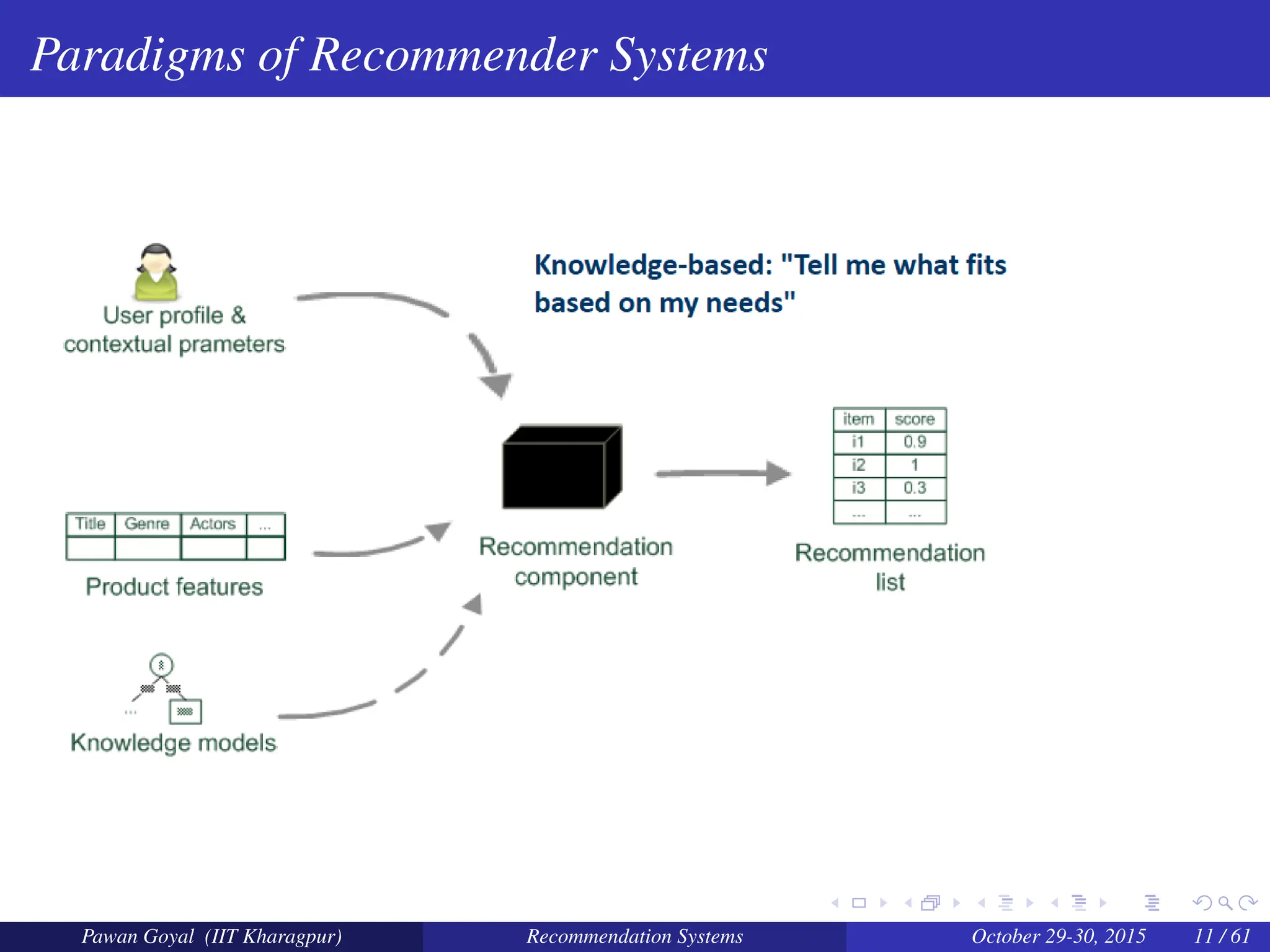
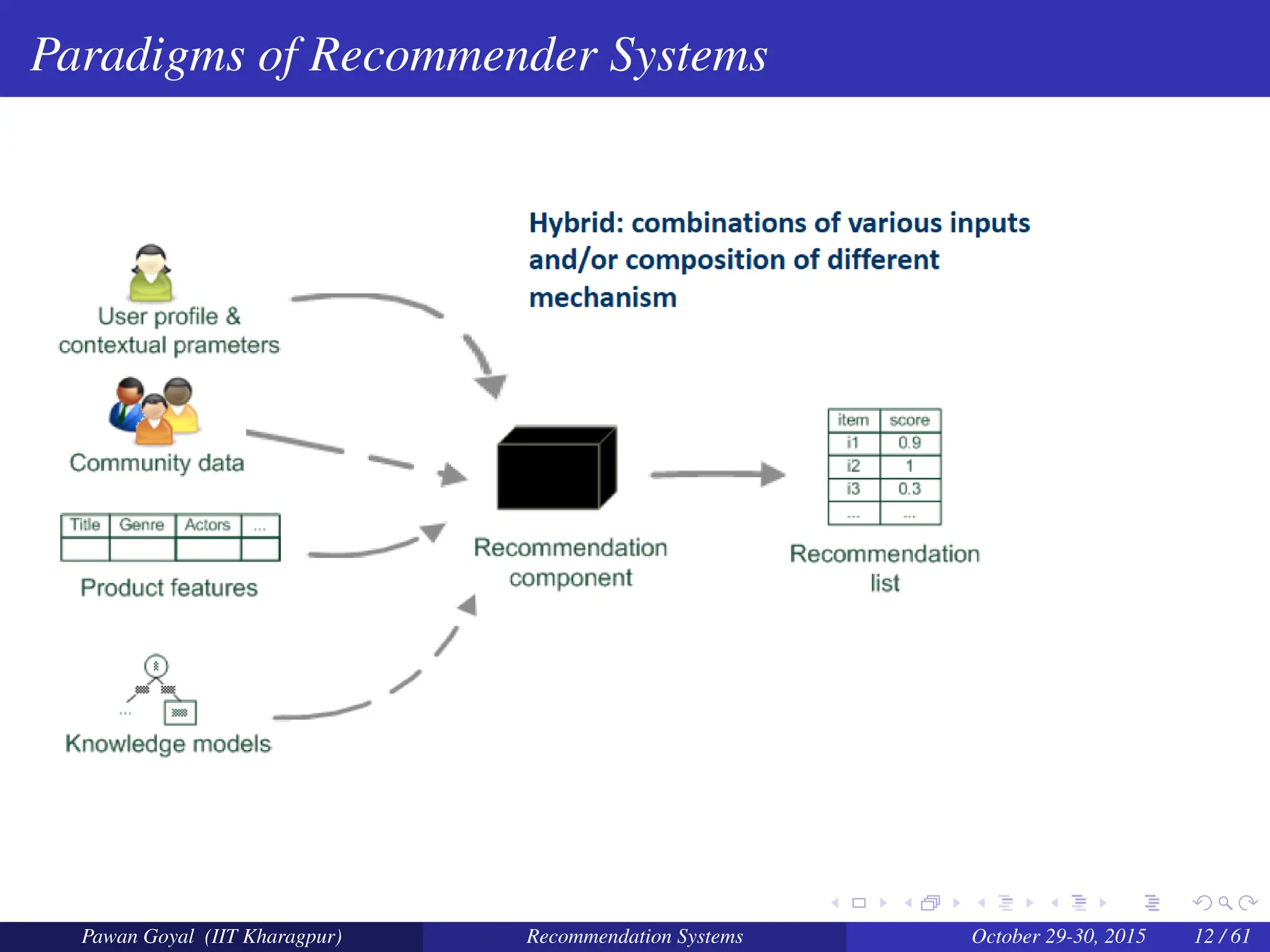
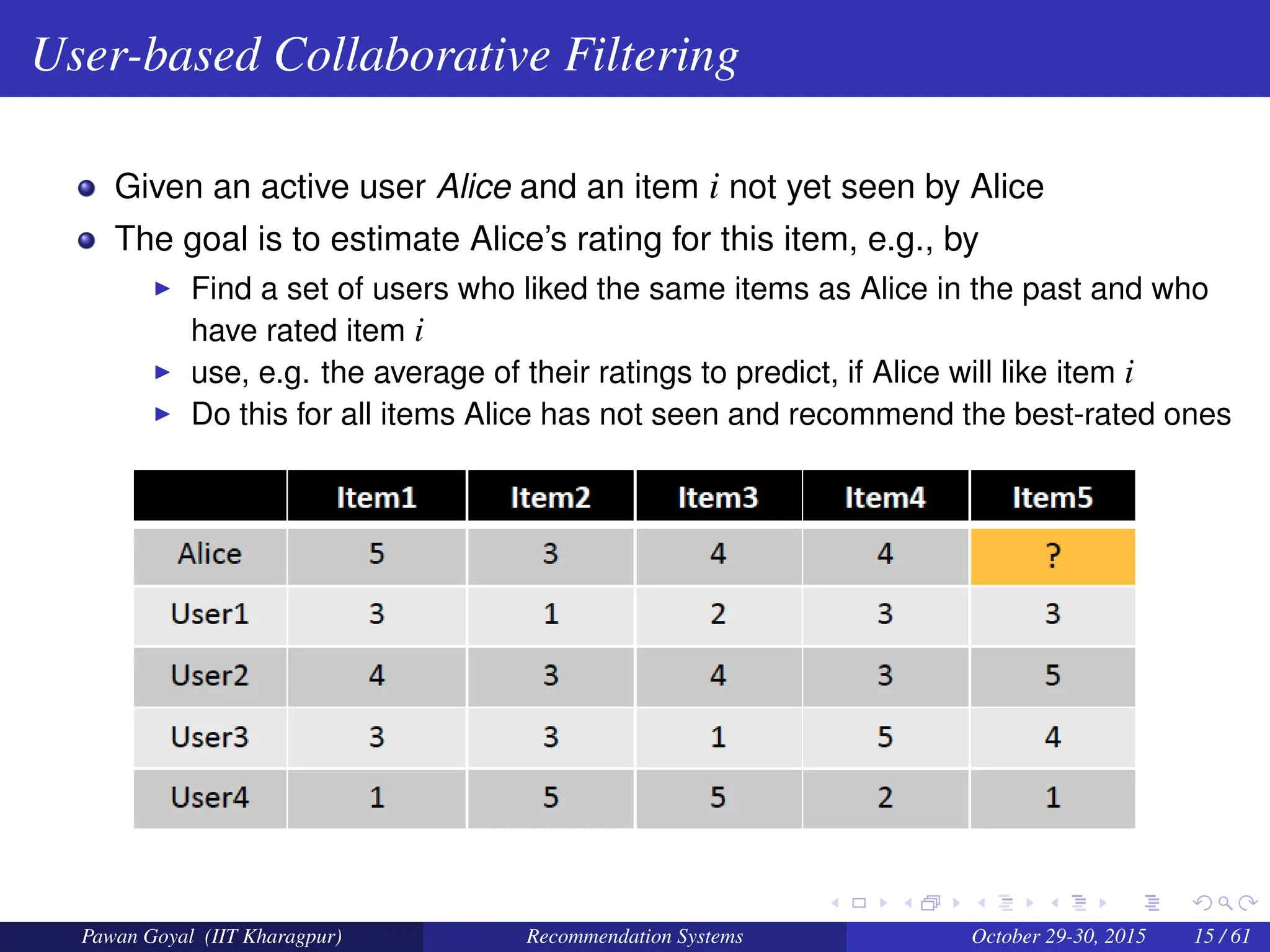
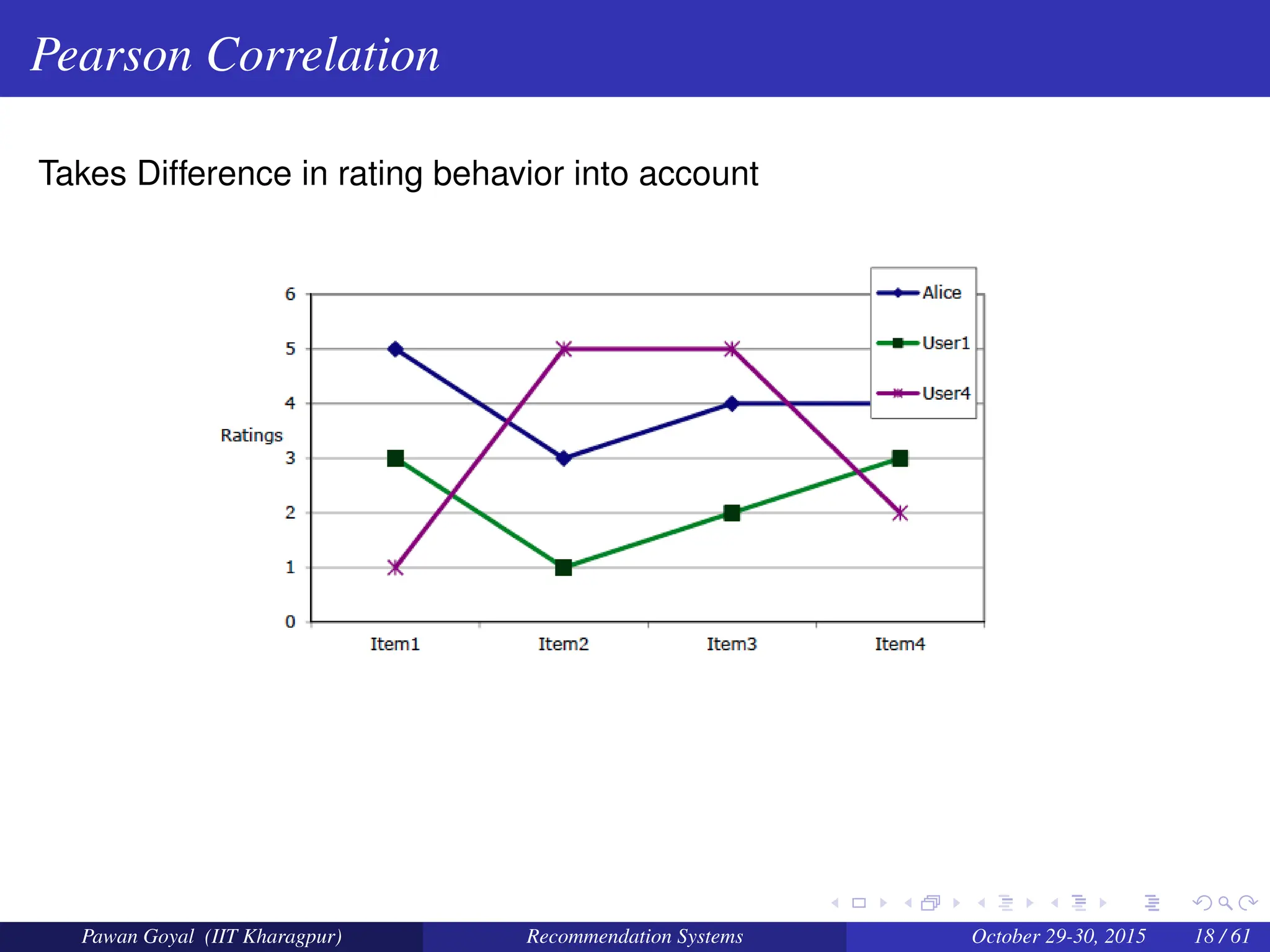
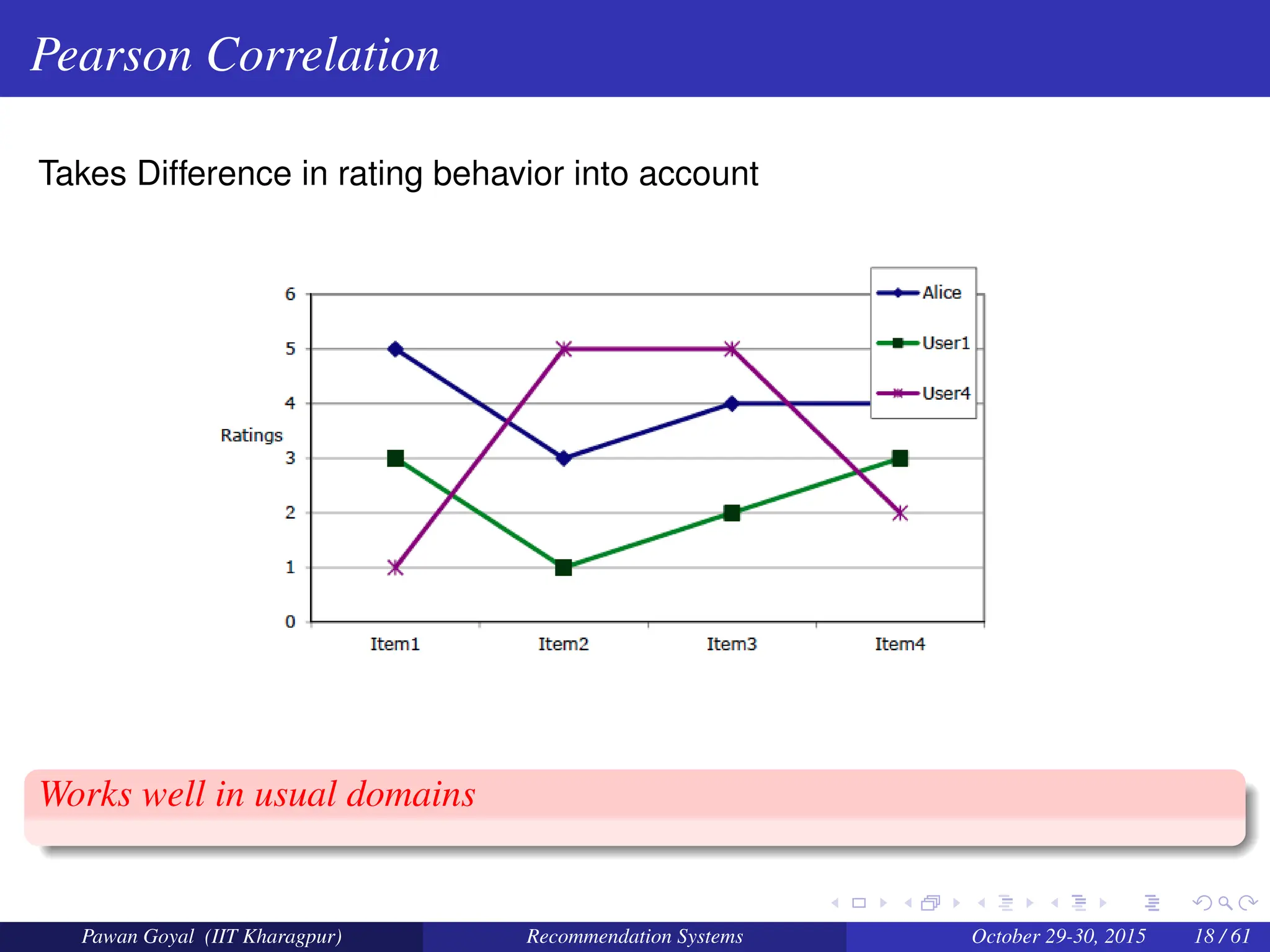
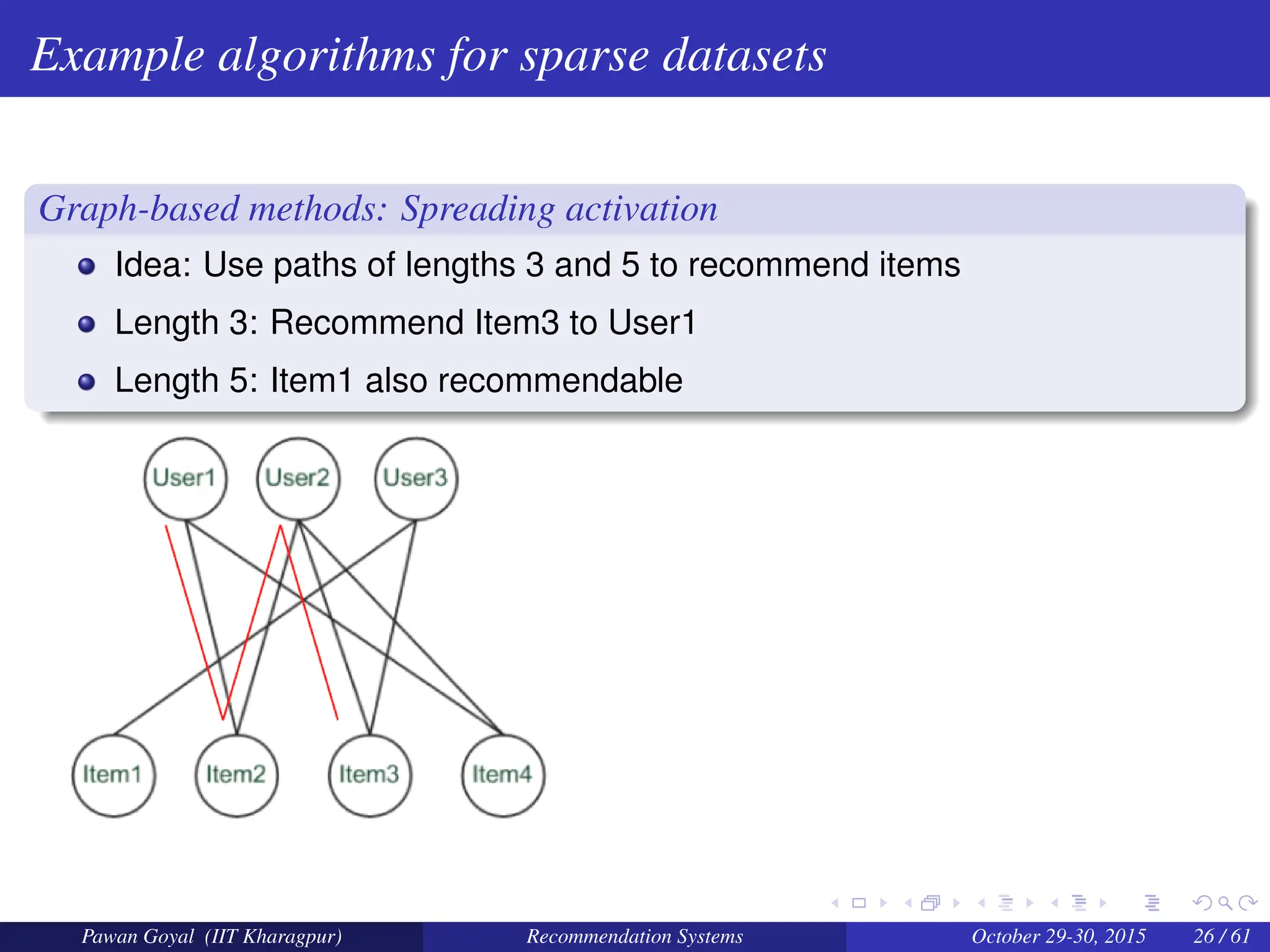
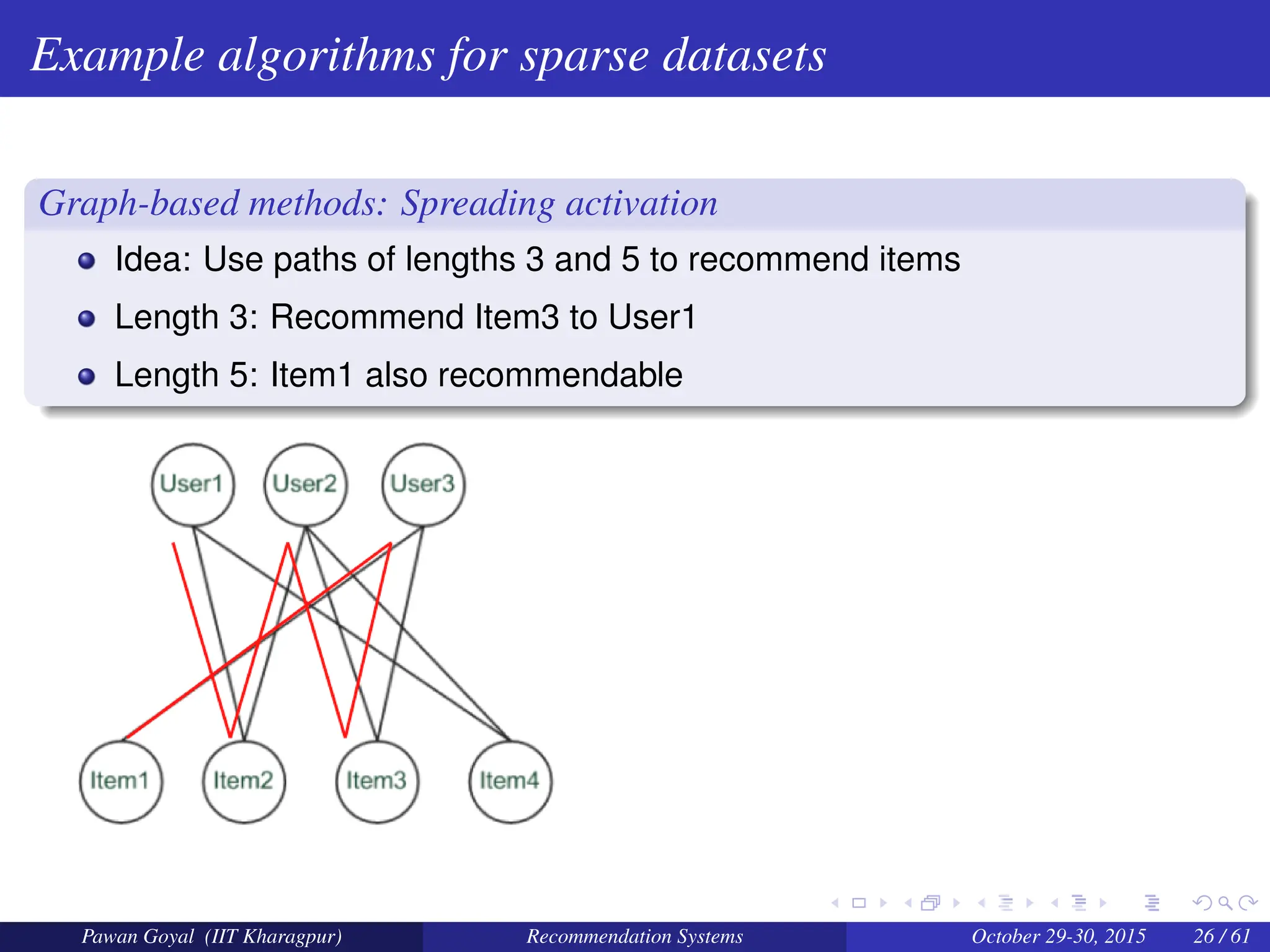
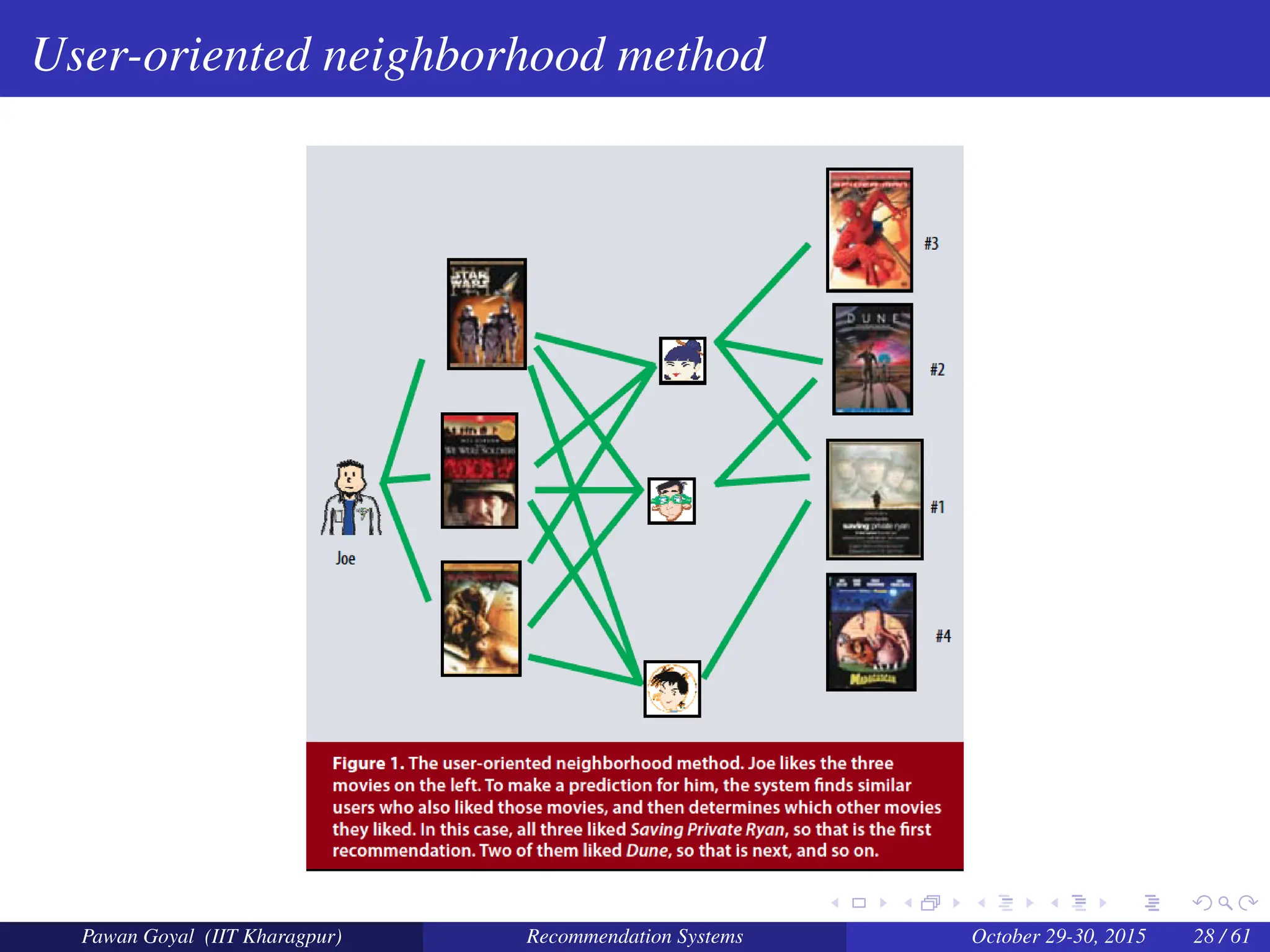
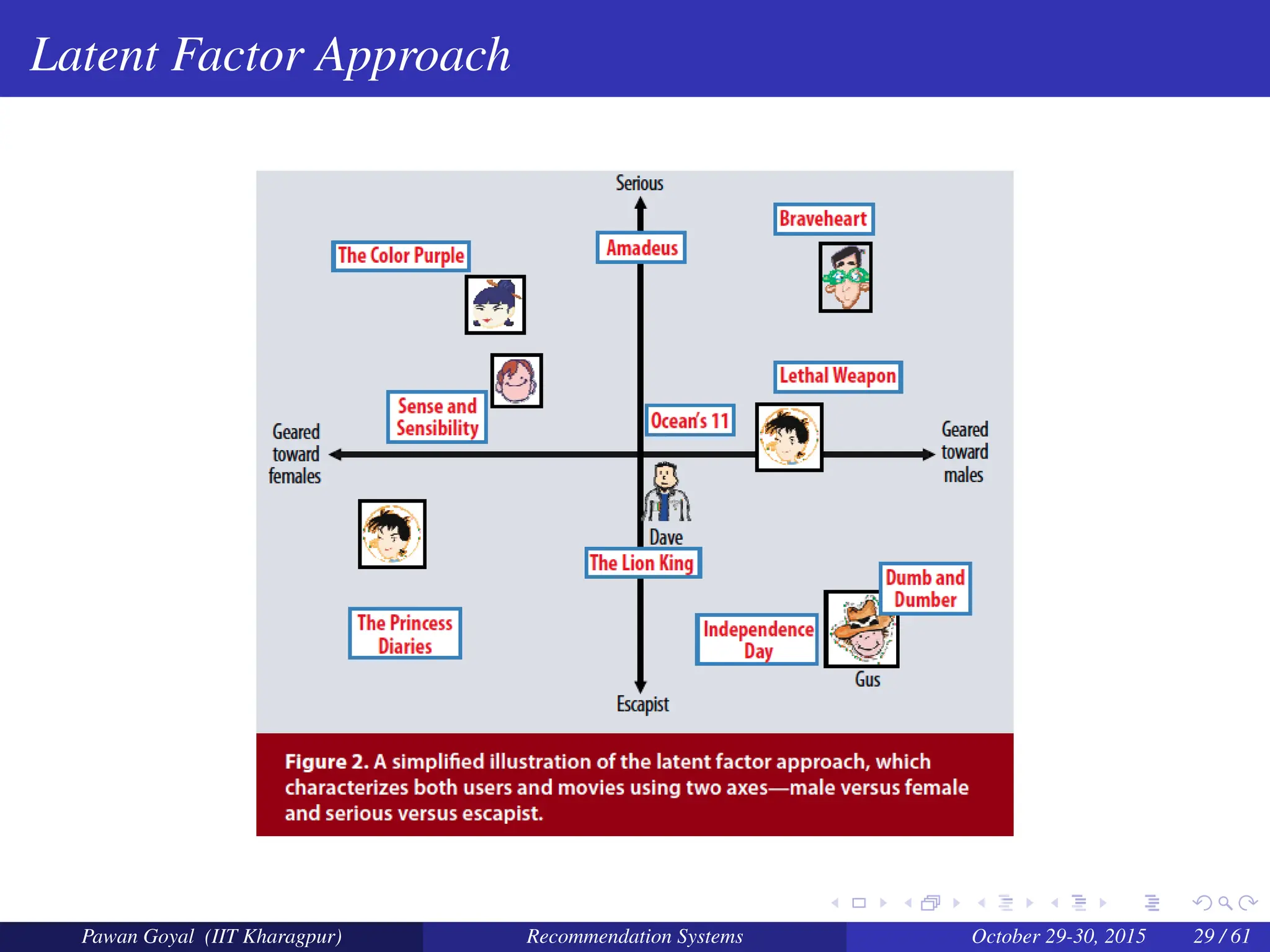
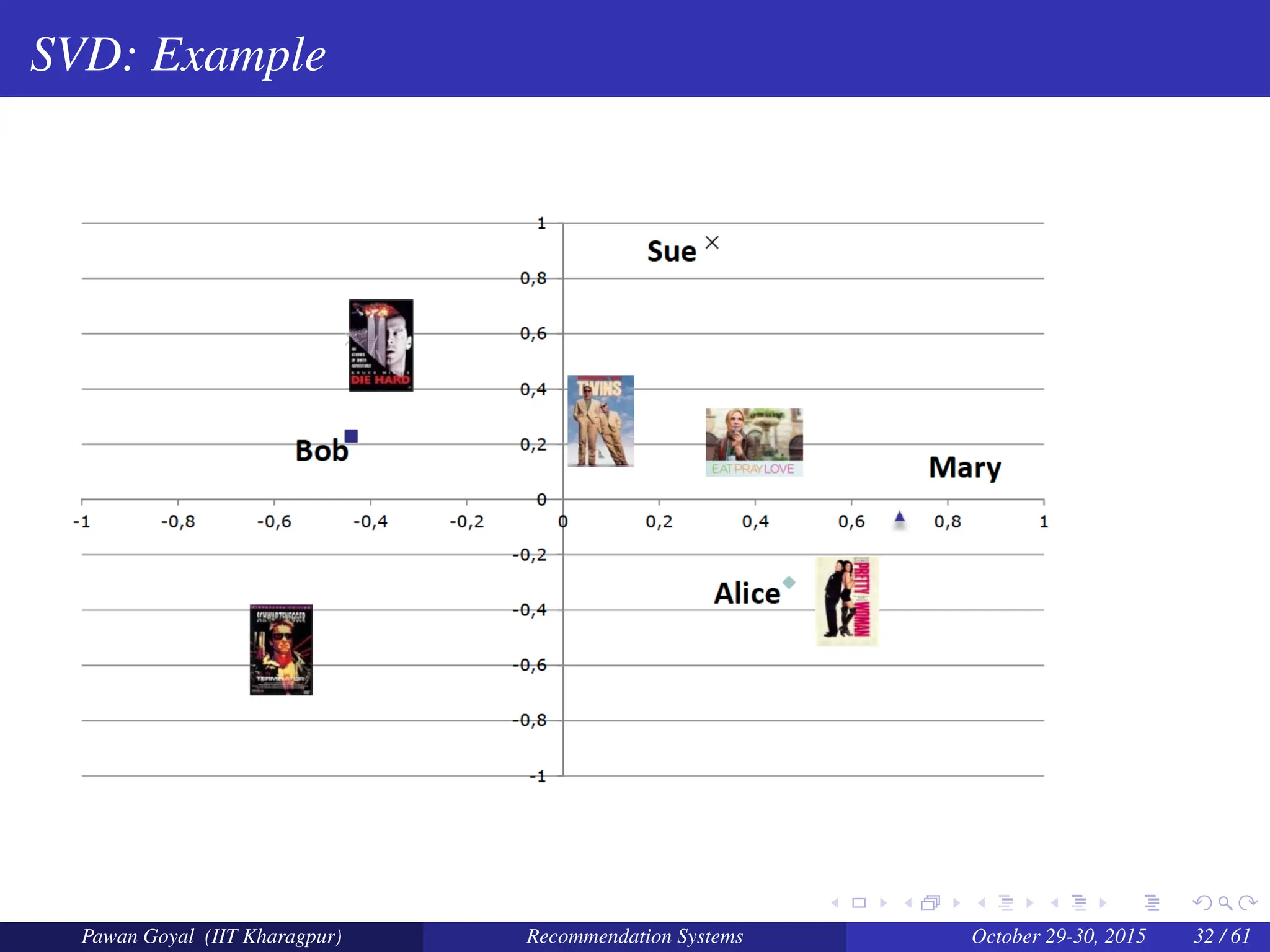
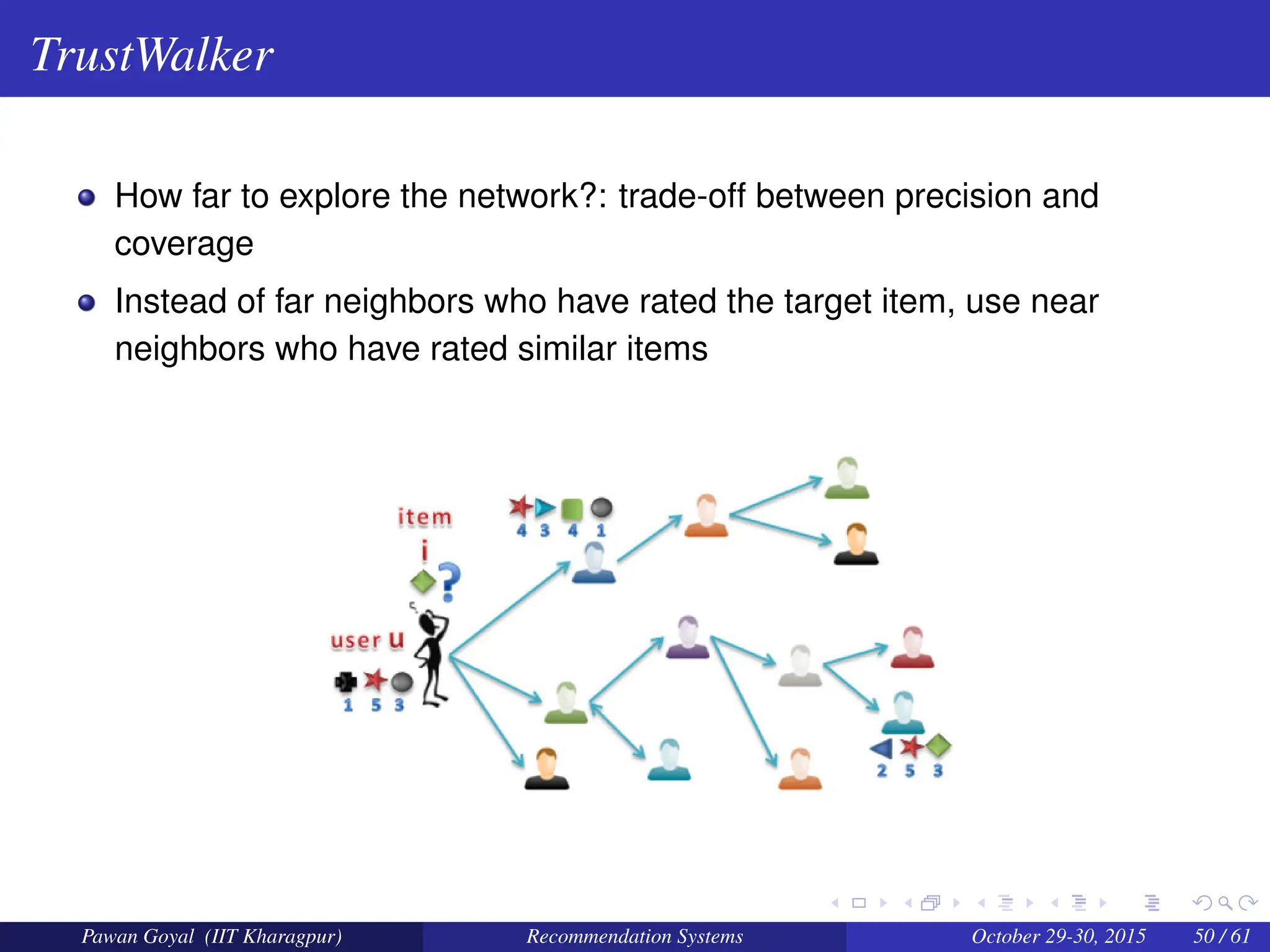
The document, presented by Pawan Goyal from IIT Kharagpur, discusses recommendation systems and their significance in the social web, emphasizing their value for both customers and providers. It outlines various approaches to creating recommendation systems, such as collaborative filtering and matrix factorization, along with their challenges like data sparsity and cold start problems. Real-world examples illustrate the effectiveness of recommendation systems in driving sales and customer engagement in platforms like Amazon and Netflix.





















































![Modeling Implicit Feedback
Boolean Implicit Feedback
N(u): set of items for which user u expressed an implicit preference
Let item i be associated with xi ∈ Rf [xi is different from qi]
The user can be characterized by the vector ∑
i∈N(u)
xi
Normalizing the sum:
∑
i∈N(u)
xi
√
|N(u)|
Pawan Goyal (IIT Kharagpur) Recommendation Systems October 29-30, 2015 42 / 61](https://image.slidesharecdn.com/recsys-250128093346-d6b8bd28/75/Introduction-to-recomender-systems-new-content-70-2048.jpg)

![Modeling Demographics
Consider boolean attributes where user u corresponds to a set of
attributes A(u)
These attributes can describe gender, age group, Zip code, income level
etc.
Let a feature vector ya ∈ Rf correspond to each attribute to describe a
user through this set as: ∑
a∈A(u)
ya
Integrating enhanced user representation in the matrix factorization model:
ˆ
rui = µ+bi +bu +qi
T
[pu +|N(u)|−0.5
∑
i∈N(u)
xi + ∑
a∈A(u)
ya]
Pawan Goyal (IIT Kharagpur) Recommendation Systems October 29-30, 2015 43 / 61](https://image.slidesharecdn.com/recsys-250128093346-d6b8bd28/75/Introduction-to-recomender-systems-new-content-72-2048.jpg)









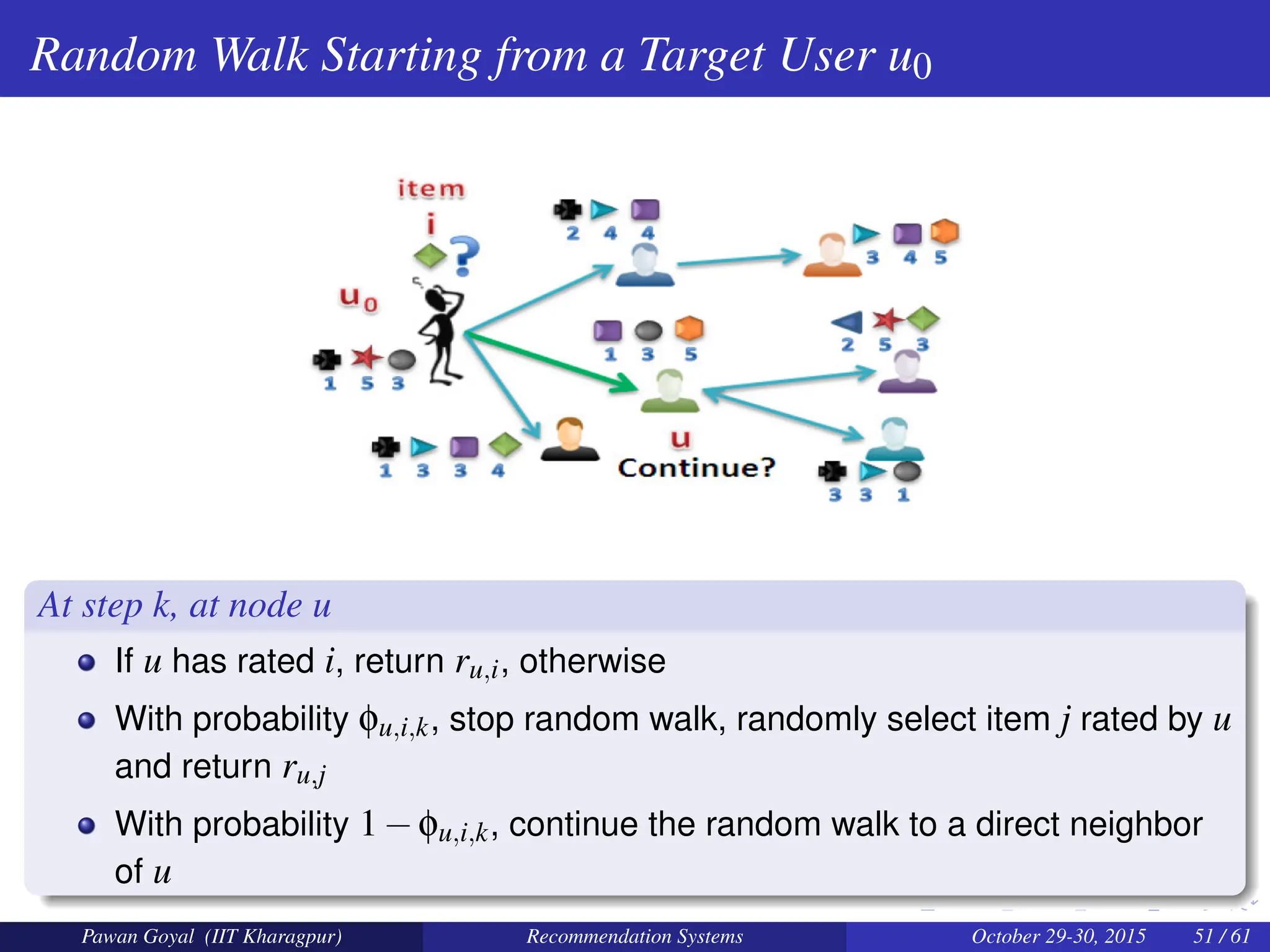










![Social Matrix Factorization
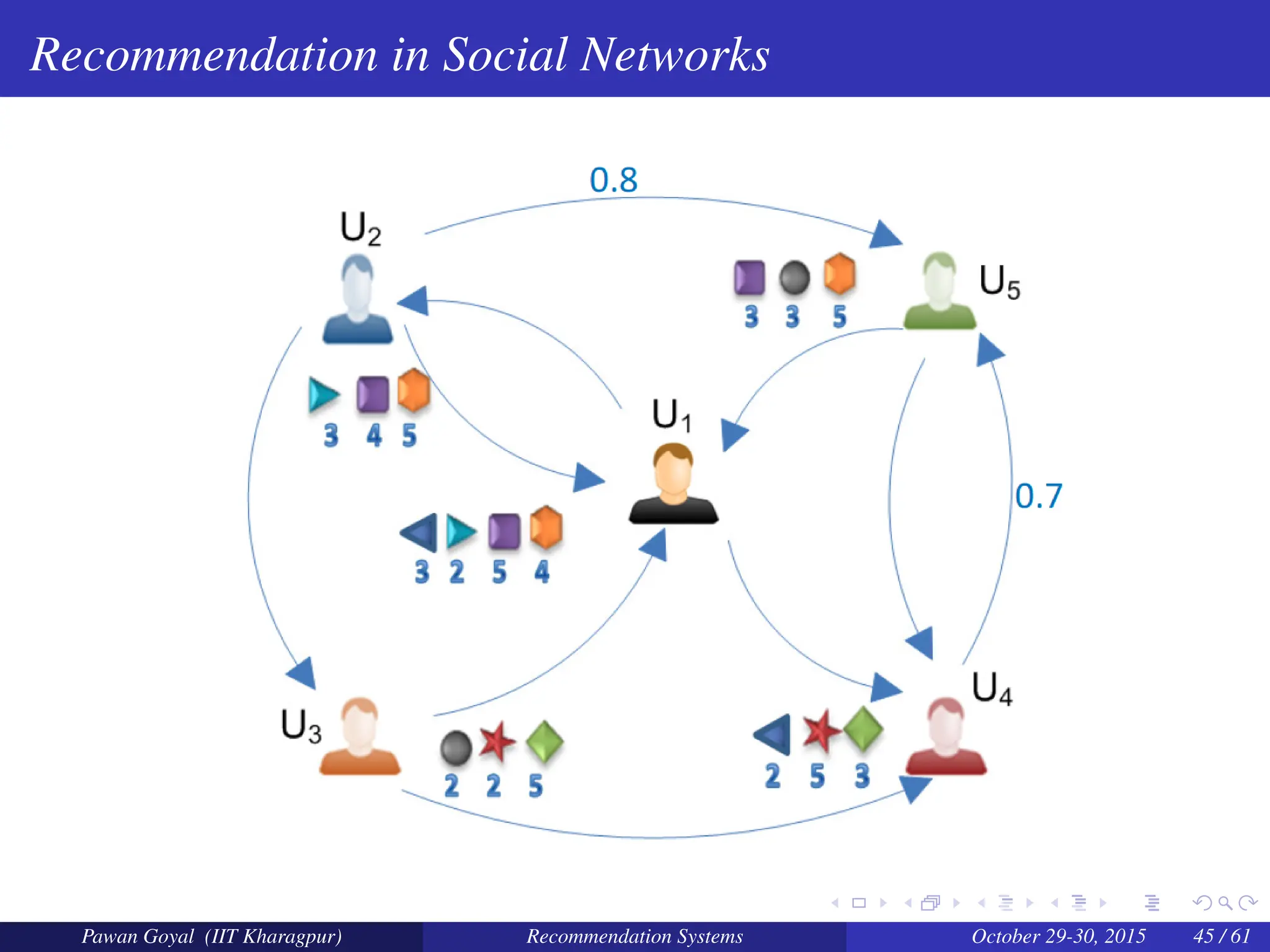
Basic Idea
Neighbors in the social network may have similar interests.
Incorporating social factors
Let the social network information be represented by a matrix S ∈ Ru0×u0 , where
u0 is the number of users.
Su,v ∈ (0,1] denotes the directed and weighted social relationship of user u with
user v
Each of the rows of the social matrix S is normalized to 1, resulting in the new
matrix S∗, such that ∑v S∗
u,v = 1 for each user u
Pawan Goyal (IIT Kharagpur) Recommendation Systems October 29-30, 2015 57 / 61](https://image.slidesharecdn.com/recsys-250128093346-d6b8bd28/75/Introduction-to-recomender-systems-new-content-95-2048.jpg)
![Social Matrix Factorization
Basic Idea
Neighbors in the social network may have similar interests.
Incorporating social factors
Let the social network information be represented by a matrix S ∈ Ru0×u0 , where
u0 is the number of users.
Su,v ∈ (0,1] denotes the directed and weighted social relationship of user u with
user v
Each of the rows of the social matrix S is normalized to 1, resulting in the new
matrix S∗, such that ∑v S∗
u,v = 1 for each user u
Modified objective function
minp∗,q∗ ∑
(u,i)∈K
(rui − ˆ
rui)2
+β ∑
all u
((qu −∑
v
S∗
u,vqv)(qu −∑
v
S∗
u,vqv)T
)
+λ(||qi||2
+||pu||2
)
Pawan Goyal (IIT Kharagpur) Recommendation Systems October 29-30, 2015 57 / 61](https://image.slidesharecdn.com/recsys-250128093346-d6b8bd28/75/Introduction-to-recomender-systems-new-content-96-2048.jpg)