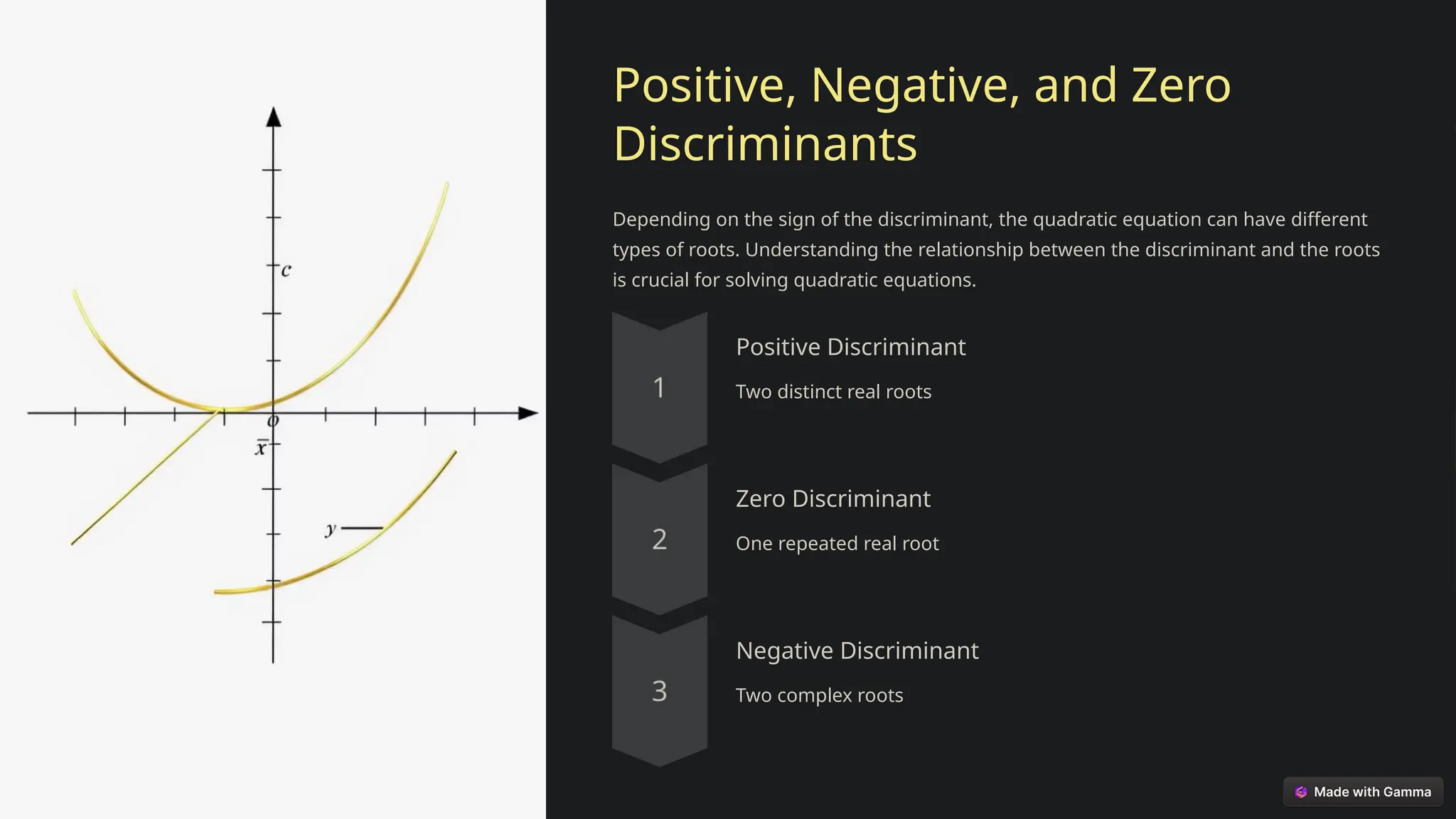
The document introduces quadratic equations, which are polynomial equations of degree 2, characterized by parabolic graphs and important in fields like physics, engineering, and economics. It explains the standard form of a quadratic equation, the discriminant, and its role in determining the nature and number of roots. The discriminant's value indicates whether roots are real or complex, distinct or repeated, and it has applications in stability analysis, trajectory prediction, and economic modeling.

1. Introduction to
Quadratic Equations
Quadratic equations are polynomial equations with a highest degree of
2. They are characterized by their parabolic graphs and play a significant
role in various fields, including physics, engineering, and economics.
by EMILY BAUTISTA

2. The Standard Form of a Quadratic Equation
The standard form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. The coefficients a, b,
and c determine the shape and position of the parabola that represents the equation.
Coefficient a
Determines the direction of the
parabola.
Coefficient b
Influences the slope and position of
the parabola.
Coefficient c
Represents the y-intercept of the
parabola.

3. The Discriminant of a
Quadratic Equation
The discriminant is a part of the quadratic formula that helps determine
the nature of the roots of a quadratic equation. It is represented by the
expression b² - 4ac.
1 Nature of Roots
The discriminant reveals
whether the quadratic
equation has real or
complex roots, and
whether these roots are
distinct or repeated.
2 Number of Solutions
The discriminant also
indicates the number of
solutions that the equation
possesses, which can be
two, one, or zero.

4. Calculating the Discriminant
To calculate the discriminant, simply substitute the values of a, b, and c
from the quadratic equation into the formula b² - 4ac. The result will be
a numerical value that can be interpreted to understand the nature of
the roots.
Equation: ax² + bx + c = 0
Discriminant: b² - 4ac

5. Interpreting the Discriminant
The discriminant provides valuable information about the roots of a quadratic equation. By analyzing the sign of the
discriminant, you can determine the nature and number of solutions.
Positive Discriminant
The equation has two distinct real
roots. The parabola intersects the x-
axis at two distinct points.
Negative Discriminant
The equation has two complex roots.
The parabola does not intersect the x-
axis.
Zero Discriminant
The equation has one repeated real
root. The parabola touches the x-axis
at one point.

6. Positive, Negative, and Zero
Discriminants
Depending on the sign of the discriminant, the quadratic equation can have different
types of roots. Understanding the relationship between the discriminant and the roots
is crucial for solving quadratic equations.
Positive Discriminant
Two distinct real roots
Zero Discriminant
One repeated real root
Negative Discriminant
Two complex roots

7. Applications of the
Discriminant
The discriminant has various applications in diverse fields. It can be used to
determine the feasibility of a solution, to analyze the stability of a system, and to
predict the behavior of physical phenomena.
Engineering
Analyzing the stability of structures
and systems.
Physics
Predicting the trajectory of projectiles
and the motion of objects.
Economics
Determining the equilibrium points in
economic models.
Finance
Analyzing the profitability of
investments.

8. Conclusion
The discriminant is a powerful tool for understanding the nature of
roots of quadratic equations. It provides valuable information that can
be applied in various fields, making it an essential concept in
mathematics.