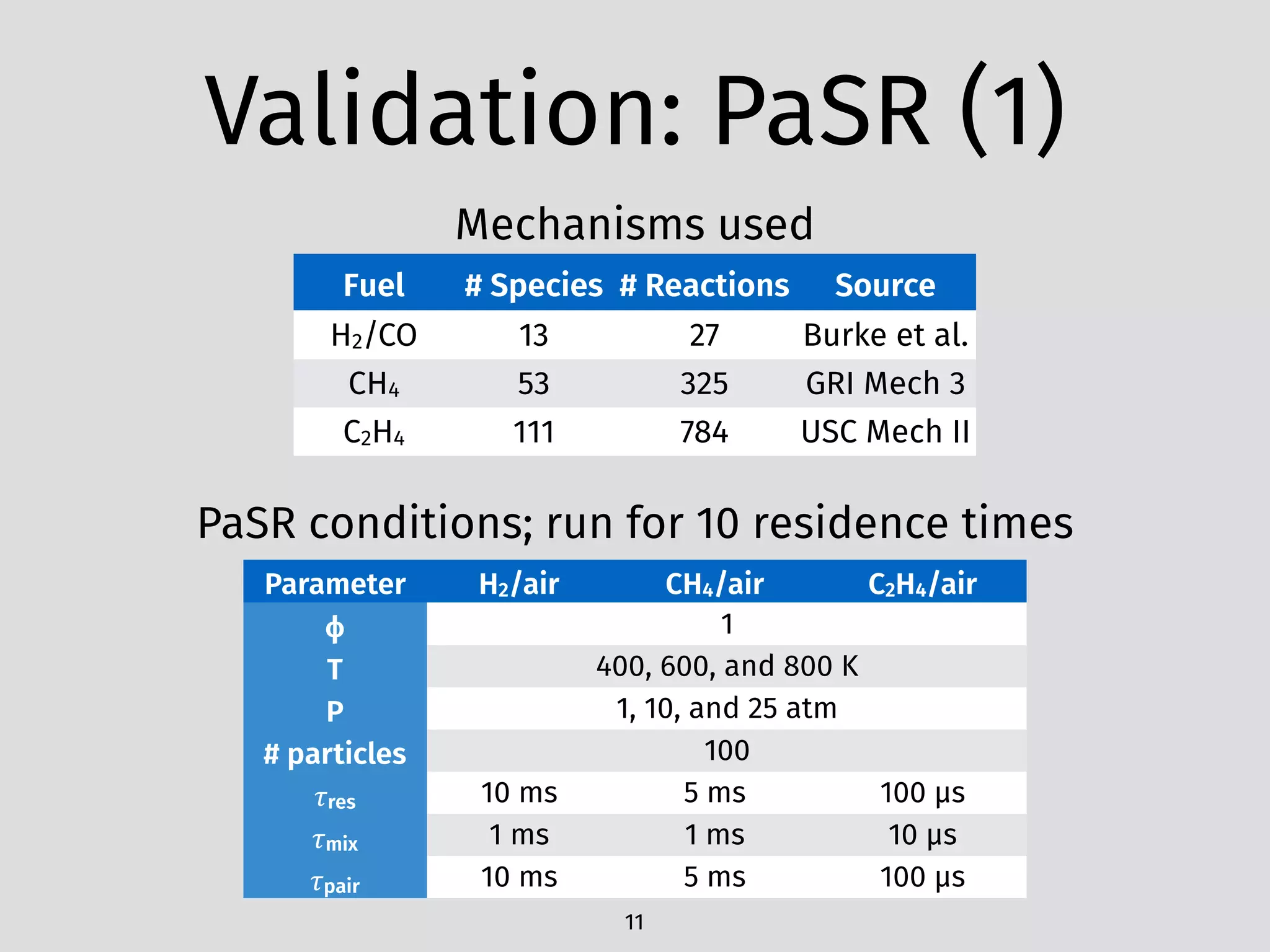
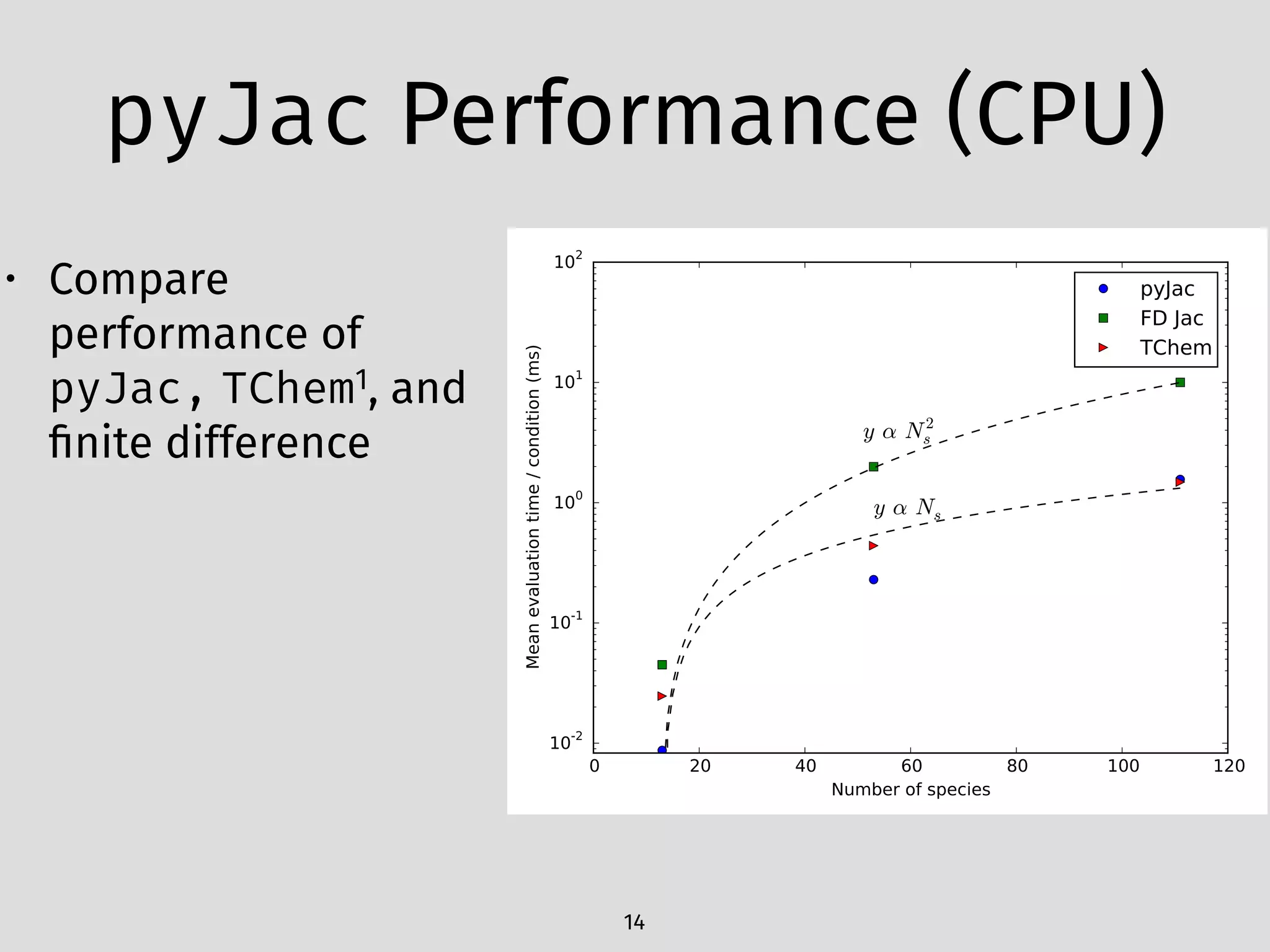
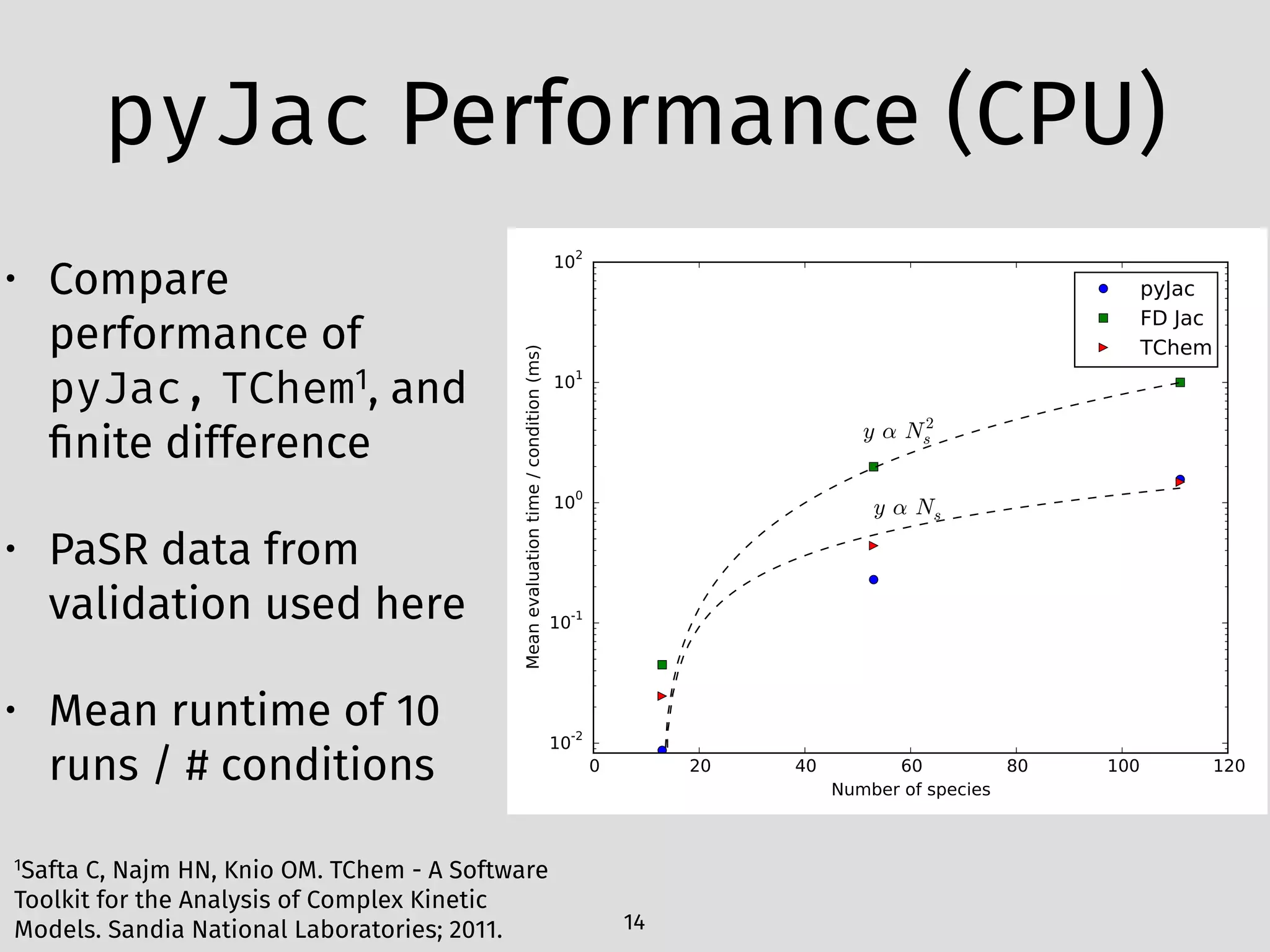
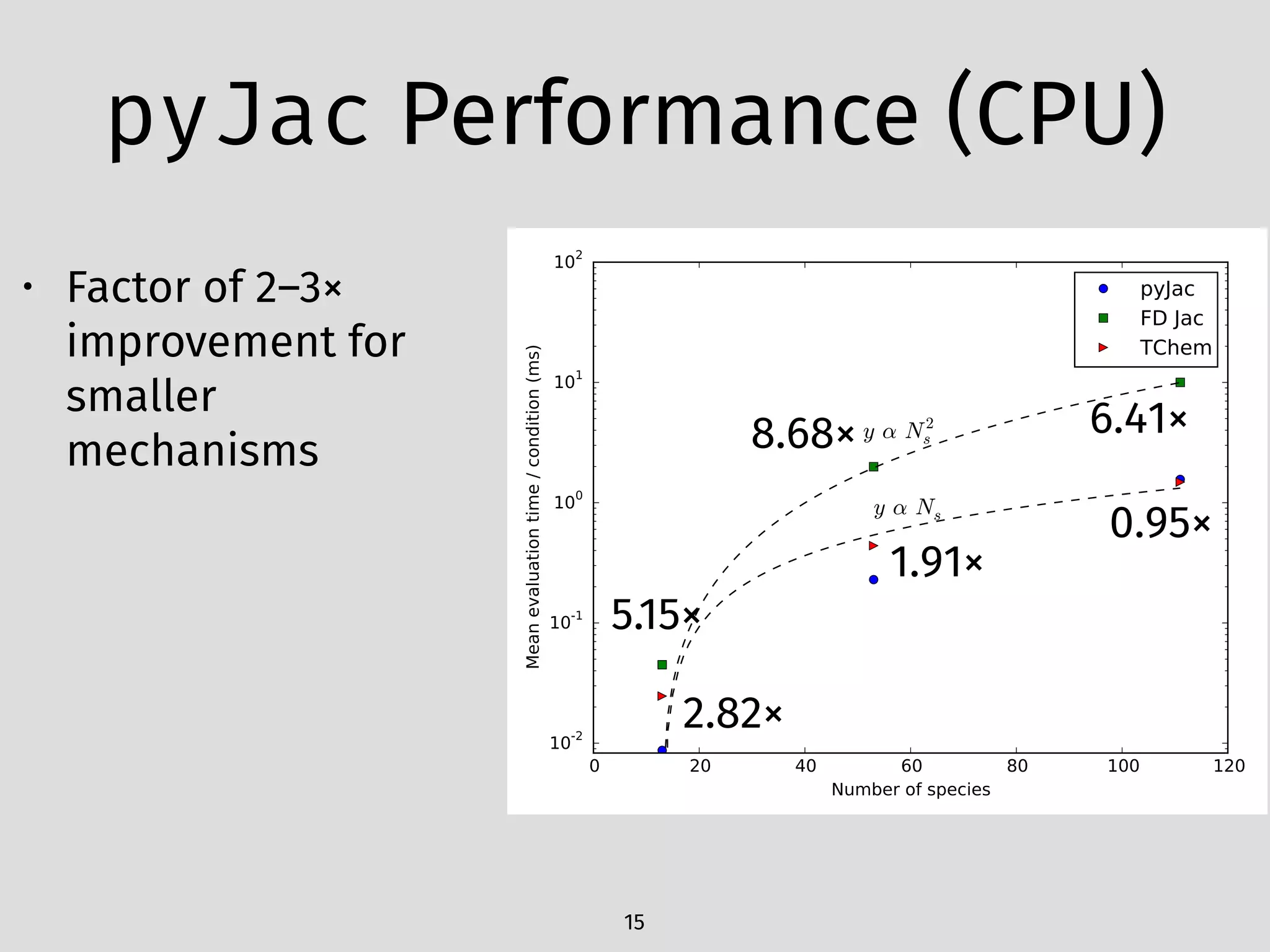
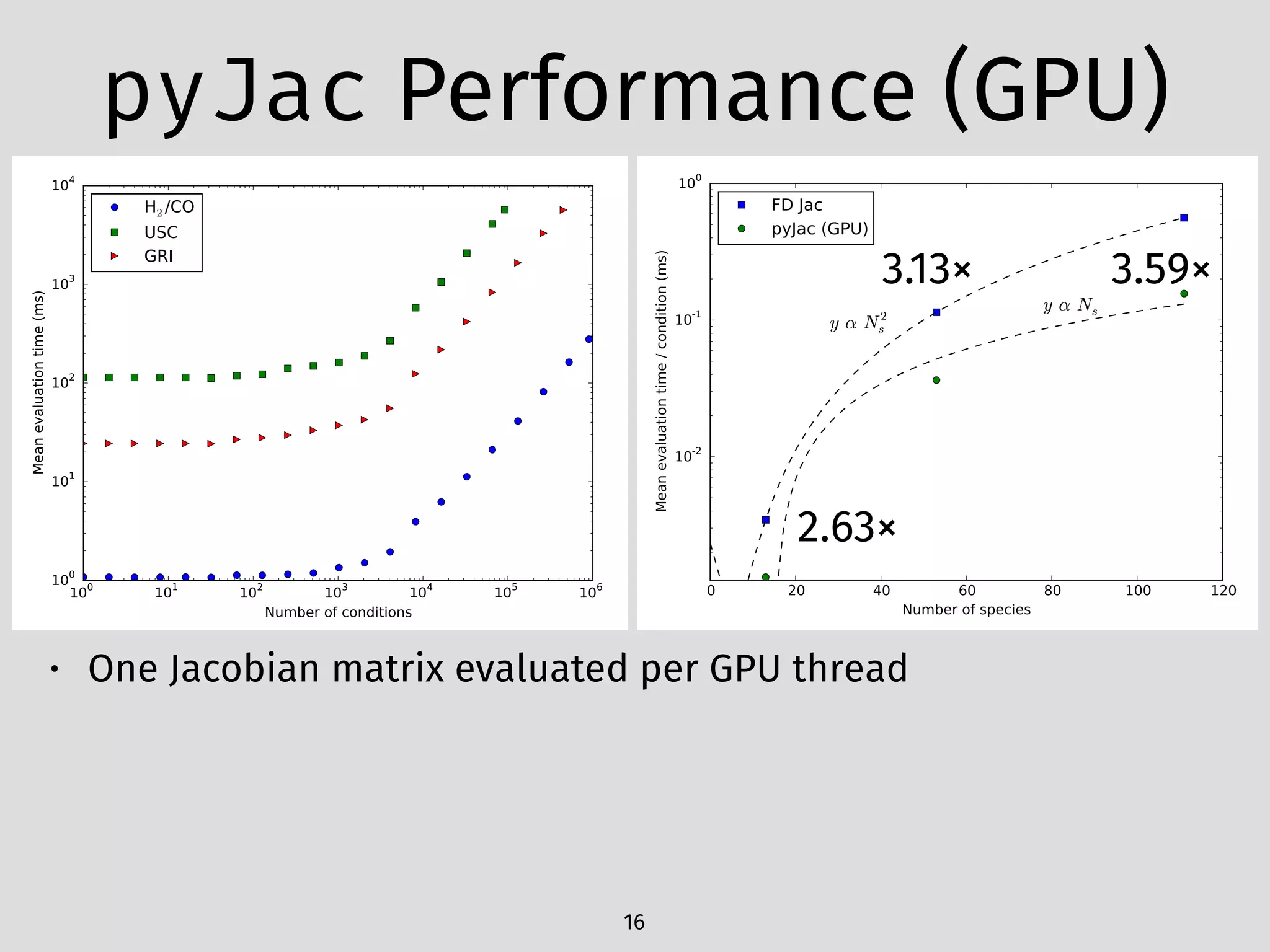
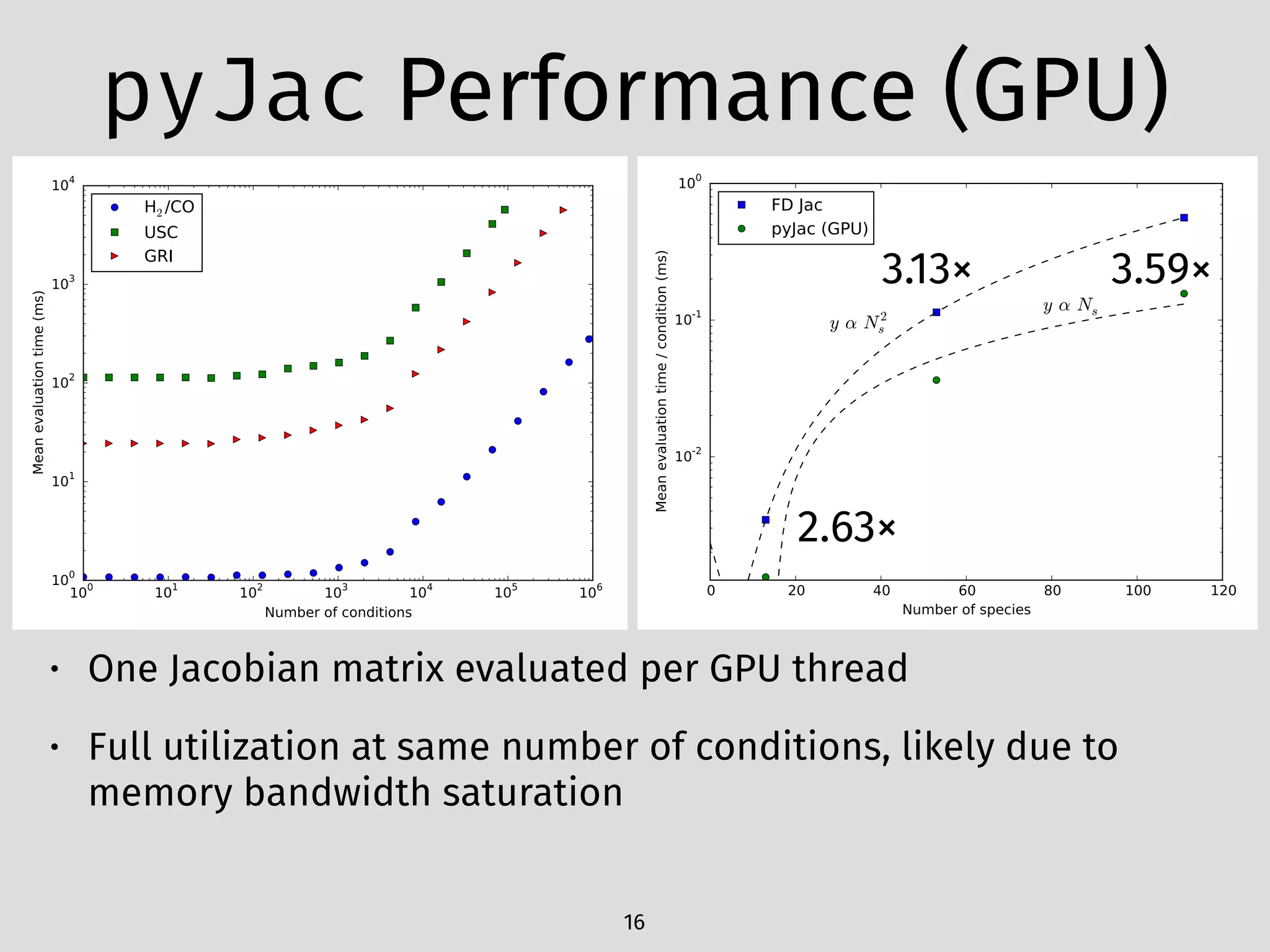
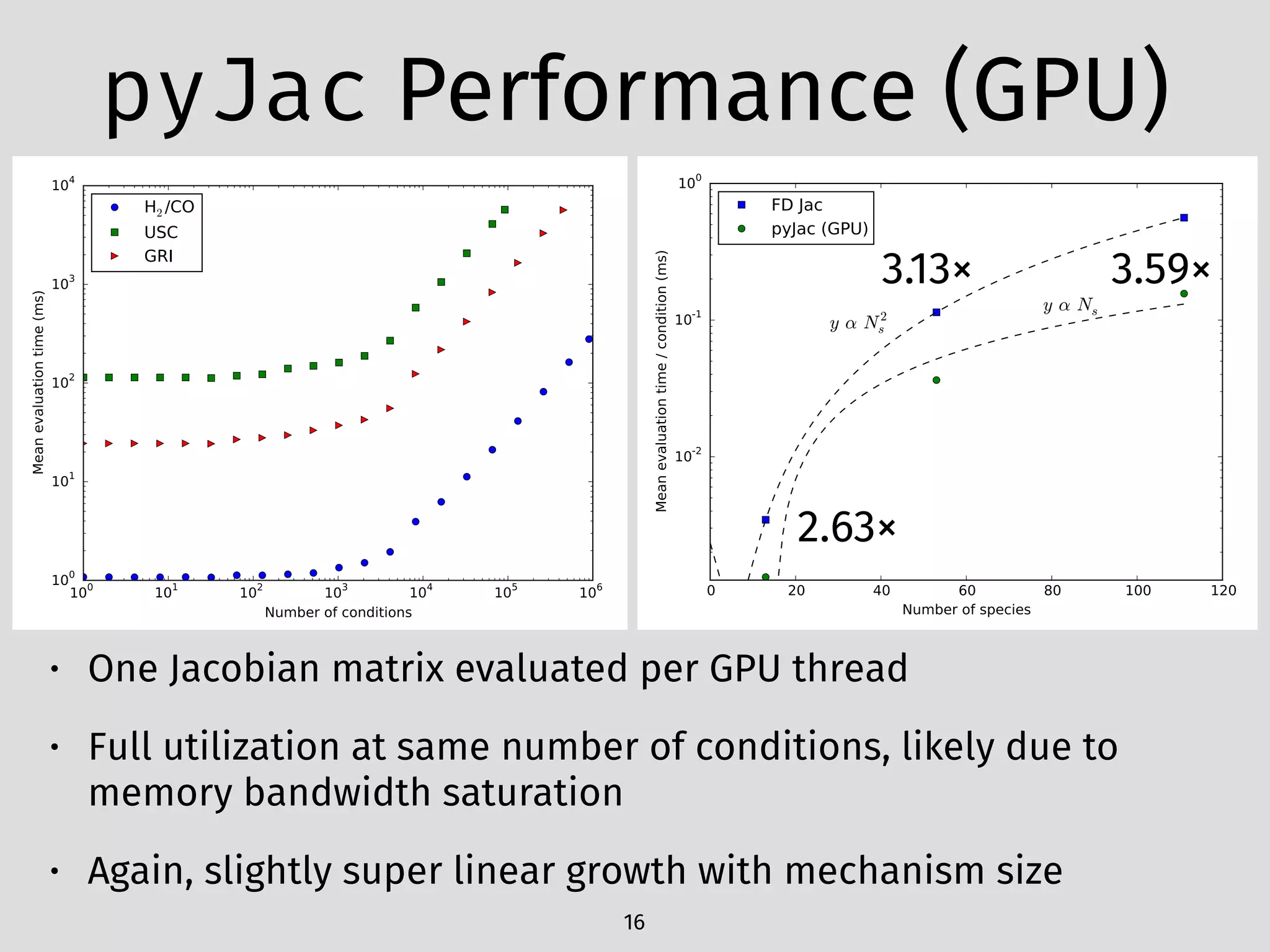
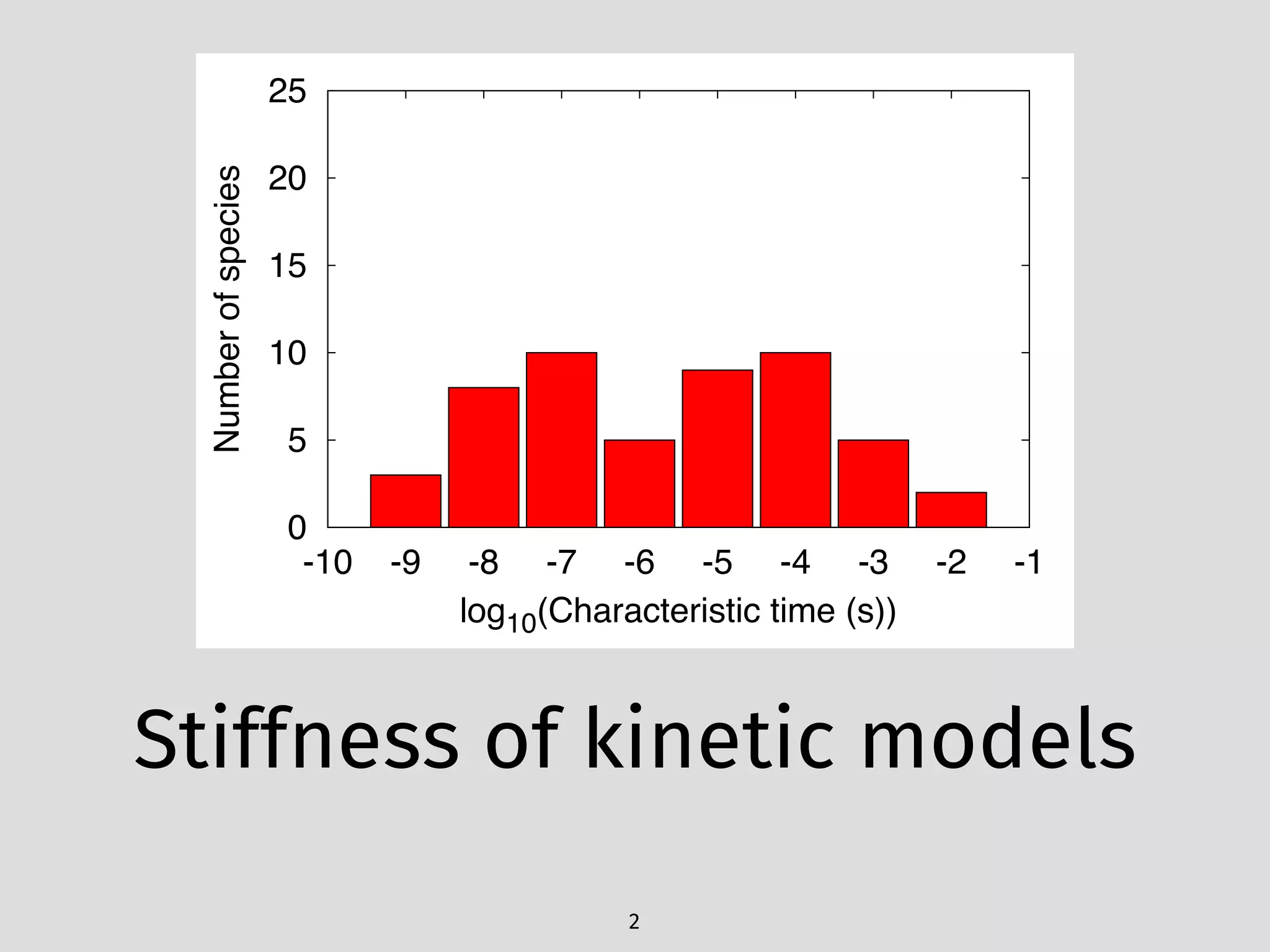
The document details an initial investigation of PyJac, an analytical Jacobian generator designed to streamline chemical kinetics integration, which is often hindered by stiffness in kinetic models. PyJac generates source code for both CPU and GPU architectures and is compatible with major chemical modeling platforms like Chemkin and Cantera. The validation results indicate that PyJac provides a significant improvement in computational efficiency over traditional methods in evaluating Jacobians for chemical reaction systems.

1. Initial investigation of pyJac:
an analytical Jacobian
generator for chemical kinetics
Kyle Niemeyer
Oregon State University
Nicholas Curtis, Chih-Jen Sung
University of Connecticut
Fall 2015 Meeting of WSSCI
5 October 2015
Funding: NSF awards 1535065 & 1534688

2. 0
5
10
15
20
25
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
Numberofspecies
log10(Characteristic time (s))
Stiffness of kinetic models
2

3. 0
5
10
15
20
25
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
Numberofspecies
log10(Characteristic time (s))
Stiffness of kinetic models
Characteristic creation times of methane oxidation
2

4. Motivation
3

5. Motivation
• Stiffness
3

6. Motivation
• Stiffness
3
implicit integration algorithms

7. Motivation
• Stiffness
• Require Jacobian matrix—repeatedly evaluated
and factorized
3
implicit integration algorithms

8. Motivation
• Stiffness
• Require Jacobian matrix—repeatedly evaluated
and factorized
• Jacobian typically obtained via finite differences
3
implicit integration algorithms

9. Motivation
• Stiffness
• Require Jacobian matrix—repeatedly evaluated
and factorized
• Jacobian typically obtained via finite differences
• Scales with (Nspecies)2
3
implicit integration algorithms

10. NumberofReactions
10
100
1000
10000
100000
Number of Species
10 100 1000 10000
before 2005
since 2005
Size of kinetic models
4

11. NumberofReactions
10
100
1000
10000
100000
Number of Species
10 100 1000 10000
before 2005
since 2005
Size of kinetic models
Hydrocarbon oxidation kinetic models poses challenges
even for 0D simulations.
4

12. NumberofReactions
10
100
1000
10000
100000
Number of Species
10 100 1000 10000
before 2005
since 2005
Size of kinetic models
Hydrocarbon oxidation kinetic models poses challenges
even for 0D simulations.
4
Transportation fuels

13. NumberofReactions
10
100
1000
10000
100000
Number of Species
10 100 1000 10000
before 2005
since 2005
Size of kinetic models
Hydrocarbon oxidation kinetic models poses challenges
even for 0D simulations.
4
2-methylalkanes

14. Motivation
5
implicit integration algorithms• Stiffness
• Require Jacobian matrix—repeatedly evaluated
and factorized
• Jacobian typically obtained via finite differences
• Scales with (Nspecies)2

15. Motivation
• Also accuracy issues for CSP, CEMA
5
implicit integration algorithms• Stiffness
• Require Jacobian matrix—repeatedly evaluated
and factorized
• Jacobian typically obtained via finite differences
• Scales with (Nspecies)2

16. Introducing pyJac
6

17. Introducing pyJac
• Accelerate chemical kinetic integration by
providing source code to evaluate chemical kinetic
Jacobian matrices analytically
6

18. Introducing pyJac
• Accelerate chemical kinetic integration by
providing source code to evaluate chemical kinetic
Jacobian matrices analytically
• pyJac capable of generating source code for CPU
and GPU architectures
6

19. Introducing pyJac
• Accelerate chemical kinetic integration by
providing source code to evaluate chemical kinetic
Jacobian matrices analytically
• pyJac capable of generating source code for CPU
and GPU architectures
• Compatible with both CHEMKIN- and Cantera-
format mechanisms
6

20. … What is a Jacobian, again?
7

21. … What is a Jacobian, again?
• Chemical kinetics governing ODE system*:
7

22. … What is a Jacobian, again?
• Chemical kinetics governing ODE system*:
7
f =
2
6
6
6
4
˙T
˙Y1
...
˙YN
3
7
7
7
5
=
2
6
6
6
4
f0 (T, ⇢, Y1, Y2, . . . , YN )
f1 (T, ⇢, Y1, Y2, . . . , YN )
...
fN (T, ⇢, Y1, Y2, . . . , YN )
3
7
7
7
5
*Constant p assumption

23. … What is a Jacobian, again?
• Chemical kinetics governing ODE system*:
• Jacobian matrix:
7
f =
2
6
6
6
4
˙T
˙Y1
...
˙YN
3
7
7
7
5
=
2
6
6
6
4
f0 (T, ⇢, Y1, Y2, . . . , YN )
f1 (T, ⇢, Y1, Y2, . . . , YN )
...
fN (T, ⇢, Y1, Y2, . . . , YN )
3
7
7
7
5
J =
df
dy
=
2
6
6
6
6
4
@ ˙T
@y
@ ˙Y1
@y
...
@ ˙YN
@y
3
7
7
7
7
5
=
2
6
6
6
6
4
@ ˙T
@T
@ ˙T
@Y1
· · · @ ˙T
@YN
@ ˙Y1
@T
@ ˙Y1
@Y1
· · · @ ˙Y1
@YN
...
...
...
...
@ ˙YN
@T
@ ˙YN
@Y1
· · · @ ˙YN
@YN
3
7
7
7
7
5
*Constant p assumption

24. Analytical Jacobian
Following a lot of math…
8
Jk+1,1 =
Wk
⇢
✓
@ ˙!k
@T
+
˙!k
T
◆
=
Wk
⇢
NreacX
i=1
⌫ki

@ci
@T
(Rf,i Rr,i) + ci
✓
@Ri
@T
+
Rf,i Rr,i
T
◆
Jk+1,j+1 =
Wk
⇢
✓
@ ˙!k
@Yj
+ ˙!k
W
Wj
◆
=
Wk
⇢
"
˙!k
W
Wj
+
NreasX
i=1
⌫ki
✓
@ci
@Yj
(Rf,i Rr,i)
+ ci
Nsp
X
l=1
⌫0
li
W
Wj
Rf,i + ljkf,i
⇢
Wl
[Xl]⌫0
li 1
Nsp
Y
n=1
n6=l
[Xn]⌫0
ni
!
Nsp
X
l=1
⌫00
li
W
Wj
Rr,i + ljkr,i
⇢
Wl
[Xl]⌫00
li 1
Nsp
Y
n=1
n6=l
[Xn]⌫00
ni
!!!#

25. Analytical Jacobian (2)
…
9
J1,1 =
Nsp
X
k=1
✓
1
cp
@hk
@T
hk
c2
p
@cp
@T
◆
Wk ˙!k
⇢
+
hk
cp
@
@T
✓
Wk ˙!k
⇢
◆
=
1
cp
Nsp
X
k=1
✓
cp,k
hk
cp
@cp
@T
◆
Wk ˙!k
⇢
+ hkJk+1,1
J1,j+1 =
Nsp
X
k=1

hk
c2
p
@cp
@Yj
Wk ˙!k
⇢
+
hk
cp
@
@Yj
✓
Wk ˙!k
⇢
◆
=
1
cp
0
@ cp,j
⇢cp
Nsp
X
k=1
hkWk ˙!k +
Nsp
X
k=1
hkJk+1,j+1
1
A
(see paper for details)

26. Optimized Evaluation
10

27. Optimized Evaluation
• General idea:
10

28. Optimized Evaluation
• General idea:
• Large portions of Jacobian entries constant for a single
reaction
10

29. Optimized Evaluation
• General idea:
• Large portions of Jacobian entries constant for a single
reaction
• Compute this portion once, and update as needed for
all species pairs
10

30. Optimized Evaluation
• General idea:
• Large portions of Jacobian entries constant for a single
reaction
• Compute this portion once, and update as needed for
all species pairs
• Potential increase in computational efficiency
10

31. Optimized Evaluation
• General idea:
• Large portions of Jacobian entries constant for a single
reaction
• Compute this portion once, and update as needed for
all species pairs
• Potential increase in computational efficiency
• Most expensive calculation can be performed once per
reaction
10

32. Optimized Evaluation
• General idea:
• Large portions of Jacobian entries constant for a single
reaction
• Compute this portion once, and update as needed for
all species pairs
• Potential increase in computational efficiency
• Most expensive calculation can be performed once per
reaction
• Species pairs updates relatively simple in comparison
10

33. Validation: PaSR (1)
11

34. Validation: PaSR (1)
11
Fuel # Species # Reactions Source
H2/CO 13 27 Burke et al.
CH4 53 325 GRI Mech 3
C2H4 111 784 USC Mech II
Mechanisms used

35. Validation: PaSR (1)
11
Parameter H2/air CH4/air C2H4/air
ϕ 1
T 400, 600, and 800 K
P 1, 10, and 25 atm
# particles 100
𝜏res 10 ms 5 ms 100 μs
𝜏mix 1 ms 1 ms 10 μs
𝜏pair 10 ms 5 ms 100 μs
PaSR conditions; run for 10 residence times
Fuel # Species # Reactions Source
H2/CO 13 27 Burke et al.
CH4 53 325 GRI Mech 3
C2H4 111 784 USC Mech II
Mechanisms used

36. Validation: PaSR (2)
12

37. Validation: PaSR (2)
• First ensured species concentrations, reaction rates, species
production rates, and derivative term matched Cantera output.
12

38. Validation: PaSR (2)
• First ensured species concentrations, reaction rates, species
production rates, and derivative term matched Cantera output.
• Jacobian validation:
12

39. Validation: PaSR (2)
• First ensured species concentrations, reaction rates, species
production rates, and derivative term matched Cantera output.
• Jacobian validation:
• Due to negative densities in some cases from finite
difference, Cantera not possible
12

40. Validation: PaSR (2)
• First ensured species concentrations, reaction rates, species
production rates, and derivative term matched Cantera output.
• Jacobian validation:
• Due to negative densities in some cases from finite
difference, Cantera not possible
• In addition, step size issues led to large errors even with
high-order finite differences
12

41. Validation: PaSR (2)
• First ensured species concentrations, reaction rates, species
production rates, and derivative term matched Cantera output.
• Jacobian validation:
• Due to negative densities in some cases from finite
difference, Cantera not possible
• In addition, step size issues led to large errors even with
high-order finite differences
• Therefore: used numdifftools* for accurate finite
difference Jacobian based on pyJac derivative output
12

42. Validation: PaSR (2)
• First ensured species concentrations, reaction rates, species
production rates, and derivative term matched Cantera output.
• Jacobian validation:
• Due to negative densities in some cases from finite
difference, Cantera not possible
• In addition, step size issues led to large errors even with
high-order finite differences
• Therefore: used numdifftools* for accurate finite
difference Jacobian based on pyJac derivative output
12
*uses multiple-term Richard extrapolation of
central differences (order 4–10)

43. Validation: PaSR (3)
13
Mechanism Sample size Mean Error Max Error
H2/CO 900,900 2.4×10-6 % 0.87%
CH4 450,900 3.4×10-3 % 0.26%
C2H4 91,800 2.2×10-5 % 3.4×10-3 %

44. Validation: PaSR (3)
• “Error”: 2-norm of relative difference with FD
13
Mechanism Sample size Mean Error Max Error
H2/CO 900,900 2.4×10-6 % 0.87%
CH4 450,900 3.4×10-3 % 0.26%
C2H4 91,800 2.2×10-5 % 3.4×10-3 %

45. Validation: PaSR (3)
• “Error”: 2-norm of relative difference with FD
• Discrepancies between analytical (CPU and GPU) and
FD Jacobian matrices small
13
Mechanism Sample size Mean Error Max Error
H2/CO 900,900 2.4×10-6 % 0.87%
CH4 450,900 3.4×10-3 % 0.26%
C2H4 91,800 2.2×10-5 % 3.4×10-3 %

46. Validation: PaSR (3)
• “Error”: 2-norm of relative difference with FD
• Discrepancies between analytical (CPU and GPU) and
FD Jacobian matrices small
• Maximum error less than 1% for all cases considered.
13
Mechanism Sample size Mean Error Max Error
H2/CO 900,900 2.4×10-6 % 0.87%
CH4 450,900 3.4×10-3 % 0.26%
C2H4 91,800 2.2×10-5 % 3.4×10-3 %

47. pyJac Performance (CPU)
14

48. pyJac Performance (CPU)
• Compare
performance of
pyJac, TChem1, and
finite difference
14

49. pyJac Performance (CPU)
• Compare
performance of
pyJac, TChem1, and
finite difference
14
1Safta C, Najm HN, Knio OM. TChem - A Software
Toolkit for the Analysis of Complex Kinetic
Models. Sandia National Laboratories; 2011.

50. pyJac Performance (CPU)
• Compare
performance of
pyJac, TChem1, and
finite difference
• PaSR data from
validation used here
14
1Safta C, Najm HN, Knio OM. TChem - A Software
Toolkit for the Analysis of Complex Kinetic
Models. Sandia National Laboratories; 2011.

51. pyJac Performance (CPU)
• Compare
performance of
pyJac, TChem1, and
finite difference
• PaSR data from
validation used here
• Mean runtime of 10
runs / # conditions
14
1Safta C, Najm HN, Knio OM. TChem - A Software
Toolkit for the Analysis of Complex Kinetic
Models. Sandia National Laboratories; 2011.

52. pyJac Performance (CPU)
15
0.95×
1.91×
2.82×
5.15×
8.68× 6.41×

53. pyJac Performance (CPU)
15
• Factor of 2–3×
improvement for
smaller
mechanisms
0.95×
1.91×
2.82×
5.15×
8.68× 6.41×

54. pyJac Performance (CPU)
15
• Factor of 2–3×
improvement for
smaller
mechanisms
• Similar/worse
performance for
largest?
0.95×
1.91×
2.82×
5.15×
8.68× 6.41×

55. pyJac Performance (CPU)
15
• Factor of 2–3×
improvement for
smaller
mechanisms
• Similar/worse
performance for
largest?
• Slight superlinear
scaling for both
0.95×
1.91×
2.82×
5.15×
8.68× 6.41×

56. pyJac Performance (GPU)
16
2.63×
3.13× 3.59×

57. pyJac Performance (GPU)
• One Jacobian matrix evaluated per GPU thread
16
2.63×
3.13× 3.59×

58. pyJac Performance (GPU)
• One Jacobian matrix evaluated per GPU thread
• Full utilization at same number of conditions, likely due to
memory bandwidth saturation
16
2.63×
3.13× 3.59×

59. pyJac Performance (GPU)
• One Jacobian matrix evaluated per GPU thread
• Full utilization at same number of conditions, likely due to
memory bandwidth saturation
• Again, slightly super linear growth with mechanism size
16
2.63×
3.13× 3.59×

60. Future Work
17

61. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
17

62. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
• Cache optimization: Reorder species/reactions to
improve cache hit rates
17

63. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
• Cache optimization: Reorder species/reactions to
improve cache hit rates
• Shared memory usage for GPU pyJac acceleration
17

64. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
• Cache optimization: Reorder species/reactions to
improve cache hit rates
• Shared memory usage for GPU pyJac acceleration
• Eventual code goals:
17

65. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
• Cache optimization: Reorder species/reactions to
improve cache hit rates
• Shared memory usage for GPU pyJac acceleration
• Eventual code goals:
• Sparse matrix formats
17

66. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
• Cache optimization: Reorder species/reactions to
improve cache hit rates
• Shared memory usage for GPU pyJac acceleration
• Eventual code goals:
• Sparse matrix formats
• Support for constant volume
17

67. Future Work
• Why do pyJac and TChem perform similarly for the
larger mechanism? Explore using larger mechanisms
• Cache optimization: Reorder species/reactions to
improve cache hit rates
• Shared memory usage for GPU pyJac acceleration
• Eventual code goals:
• Sparse matrix formats
• Support for constant volume
• Code generation in Fortran and Matlab
17

68. Conclusions
18

69. Conclusions
• Developed analytical, exact Jacobian generator
that supports both CPU and GPU platforms (and
all modern reaction rate formulations
18

70. Conclusions
• Developed analytical, exact Jacobian generator
that supports both CPU and GPU platforms (and
all modern reaction rate formulations
• pyJac v0.9-beta available today:
https://github.com/kyleniemeyer/pyJac
18

71. Thank you! Questions?
19

72. Thank you! Questions?
19
?

73. Thank you! Questions?
19
?Looking for graduate students!

74. Backup Slides
20

75. PaSR
• Cantera-based PaSR implementation; premixed combustion
with fresh fuel/air mixture & pilot streams
• Pairwise mixing, reaction fractional steps, inflow/outflow
events
21

76. Richardson Extrapolation
• A simple forward first order derivative approximation:
• Rewritten as:
• Now let
• Finally, combining these:
• Combined with use of high-order derivatives, this approach
allows use of larger step sizes.
22
f0
(x) =
f(x + h) f(x)
h
+
h
2
f00
(x) +
h2
3!
f000
(x) . . .
f0
(x) = Lh +
h
2
f00
(x) +
h2
3!
f000
(x) . . .
f0
(x) = Lh/2 +
h
4
f00
(x) +
h2
4 · 3!
f000
(x) . . .
f0
(x) = 2 ⇥ (2) (1) = 2Lh/2 Lh + O(h2
) + . . .