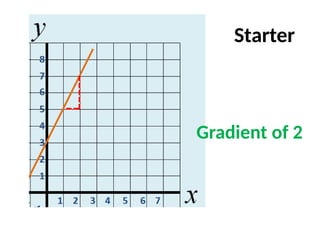
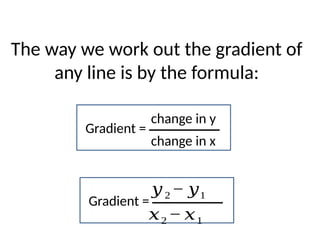
The document outlines the objectives and activities related to understanding the equations of lines, particularly focusing on lines that are perpendicular to given lines and passing through specified points. It provides examples of finding the equations of perpendicular lines and explains the concept of gradient as a measure of line steepness. Additionally, it includes exercises intended for practice and homework.

1. Chapter 15.6
Points and Lines

2. Gradient of 2
Starter

3. Objective
• Find the equation of the line
perpendicular and passing through
the point.
• Find the gradient of a line

4. Objective 1

5. Saturday
31 August
2024
Objective 2:Find the equation of graphs parallel or
perpendicular to others and passing through a specific
point.
Find the equation of the line perpendicular to y = - x – 2 and
passing through the point (2, 9).
What is the gradient
of the line given…?
y = - x – 2
= -
y = 3x + c
To find the value of c,
substitute your pair of
coordinates into the
equation…
sub (2, 9)

y = 3x + c
9 = 3(2) +
c
9 = 6 + c
3 = c
So, the equation is … y = 3x + 3.
…remember
the negative
reciprocal…!

6. Saturday
31 Augus
t 2024
Perpendicular Lines.
Equations of Perpendicular Lines:
Find the equation of the line perpendicular to y = 2x + 4 and
passing through the point (3, 7).
What is the gradient
of the line given…?
y = 2x + 4
= 2
y = x + c
To find the value of c, substitute
your pair of coordinates into the
equation…
sub (3, 7)

7 = (3) + c
7 = + c
= c
So, the equation is … y = x +.
…remember the
negative
reciprocal…!
= c

7. Saturday
31 Augus
t 2024
Activity 1: Perpendicular Lines.
1) Find the equation of the line which is perpendicular
to y = x + 1 and passes through (5, 21).
2) Find the equation of the line which is perpendicular
to 10y + 5x = 3 and passes through (-7, -1).
3) Find the equation of the line which is perpendicular
to 2x = 8 – y and passes through (16, 47).
4) Find the equation of the line which is perpendicular
to 6 + 8y = 3x and passes through (12, -37).

8. Objective 2

9. What is gradient?
Gradient is the measure of how steep a
line is. The bigger the gradient, the
steeper the line.
Introduction: Gradient of Straight Line

10. The way we work out the gradient of
any line is by the formula:
change in y
change in x
Gradient =
𝑦2− 𝑦1
Gradient =
𝑥2 − 𝑥1

11. Find the gradient of the line through each
pair of points
• A) ( 4,0) and (6,6)
• B) (0,3) and (8,7)

12. Activity 2

13. Homework
• Page no. 273 Exercise 15F Q1. Choose any 3
sub-questions.