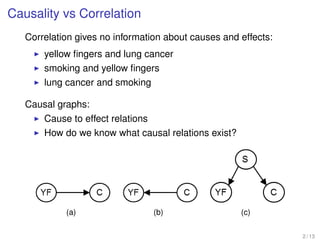
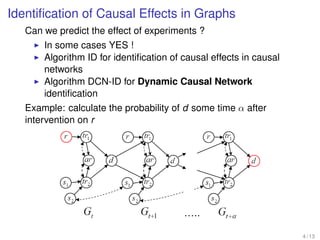
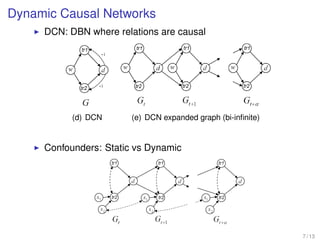
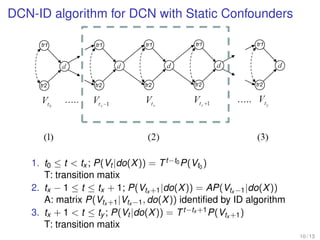
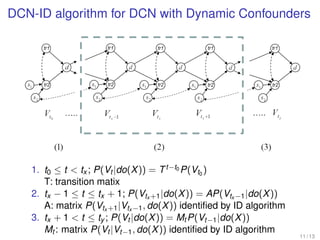
The document discusses algorithms for identifying causal effects in dynamic causal networks (DCNs). It presents the DCN-ID algorithm, which can identify causal effects in DCNs with either static or dynamic confounders. For DCNs with static confounders, the algorithm shows that the network recovers time-invariant behavior after an intervention. However, for DCNs with dynamic confounders, the algorithm reveals that the network does not necessarily recover time-invariant behavior after intervention. The algorithm provides a complete method for identifying causal effects in DCNs regardless of whether confounders are static or dynamic.

1. Identifiability in Dynamic Causal Networks
Gilles Blondel, Marta Arias, Ricard Gavaldà
Universitat Politècnica de Catalunya, Barcelona
4th Graph-TA, Barcelona, March 2016
Contact: gblondel@cs.upc.edu
1 / 13

2. Causality vs Correlation
Correlation gives no information about causes and effects:
yellow fingers and lung cancer
smoking and yellow fingers
lung cancer and smoking
Causal graphs:
Cause to effect relations
How do we know what causal relations exist?
(a) (b) (c)
2 / 13

3. Causal Graphs and Interventions
How to scientifically establish causal links and graphs?
Example - World Heatlh Organisation: "Processed meat
causes cancer"
Result based on experiments (animals, cell based
research); not on observation alone
Domain Experiments:
Intervention: force a variable X and measure the effects
All observed and hidden causes of X are disabled
Confounder: hidden variable, having an effect on several
observed variables
Experiments allow us to disable confounders
3 / 13

4. Identification of Causal Effects in Graphs
Can we predict the effect of experiments ?
In some cases YES !
Algorithm ID for identification of causal effects in causal
networks
Algorithm DCN-ID for Dynamic Causal Network
identification
Example: calculate the probability of d some time α after
intervention on r
4 / 13

5. Causality and Causal Graphs
Causality:
Statistics and machine learning: statistical correlation
Causality: cause to effect relationships
Statistical correlation is only a hint towards causal relations
Causes may be more interesting than correlations (causes
of cancer more interesting than correlation to cancer)
Causal Graphs:
Bayesian networks
Used to describe causal relationships
Edges represent causality
Directed Acyclic Graphs (DAG)
Application: predict the effect of interventions
5 / 13

6. Judea Pearl’s do-calculus
Judea Pearl - Causality: models, reasoning and inference
Intervention: force a variable and evaluate the effect
We experiment on the domain by controlling variable X
Expressed as do(X), like in P(Y/do(X))
Observed causes of X are disabled
Unobserved (confounding) causes of X are disabled
P(Y/do(X)) is different from P(Y/X)
The three rules of do-calculus:
1. P(Y|Z, W, do(X)) = P(Y|W, do(X)) if (Y ⊥ Z|X, W)GX
2. P(Y|W, do(X), do(Z)) = P(Y|Z, W, do(X)) if
(Y ⊥ Z|X, W)GXZ
3. P(Y|W, do(X), do(Z)) = P(Y|W, do(X)) if
(Y ⊥ Z|X, W)GXZ(W)
6 / 13

7. Dynamic Causal Networks
DCN: DBN where relations are causal
(d) DCN (e) DCN expanded graph (bi-infinite)
Confounders: Static vs Dynamic
7 / 13

8. Causal Graph Identification
Identification of causal effects: Computing the probability
distribution P(Y|do(X)) from the observed probability
distributions in the graph
Not all graphs are identifiable, depending on confounders
ID algorithm (Shiptser / Pearl)
Inputs: causal graph G, variable sets X and Y, and a
probability distribution P over the observed variables in G
Output: an expression for P(Y|do(X)) without any do()
terms, or fail
8 / 13

9. DCN analysis with do calculus
How to apply do-calculus to DCN:
Exploit time slice d-separation by careful conditioning
Heavy dependence on static vs dynamic confounders
Some examples:
Future observations: observing travel delay today makes
observing future traffic irrelevant to yesterday’s traffic
Future actions: traffic control next week has no causal
effect on traffic flow this week
Past actions: observing traffic flow in two days caused by
traffic control mechanisms tomorrow, and conditioned on
the traffic delay today. Any traffic controls applied before
today are irrelevant.
9 / 13

10. DCN-ID algorithm for DCN with Static Confounders
1. t0 ≤ t < tx ; P(Vt |do(X)) = Tt−t0 P(Vt0
)
T: transition matix
2. tx − 1 ≤ t ≤ tx + 1; P(Vtx +1|do(X)) = AP(Vtx −1|do(X))
A: matrix P(Vtx +1|Vtx −1, do(X)) identified by ID algorithm
3. tx + 1 < t ≤ ty ; P(Vt |do(X)) = Tt−tx +1P(Vtx +1)
T: transition matix
10 / 13

11. DCN-ID algorithm for DCN with Dynamic Confounders
1. t0 ≤ t < tx ; P(Vt |do(X)) = Tt−t0 P(Vt0
)
T: transition matix
2. tx − 1 ≤ t ≤ tx + 1; P(Vtx +1|do(X)) = AP(Vtx −1|do(X))
A: matrix P(Vtx +1|Vtx −1, do(X)) identified by ID algorithm
3. tx + 1 < t ≤ ty ; P(Vt |do(X)) = Mt P(Vt−1|do(X))
Mt : matrix P(Vt |Vt−1, do(X)) identified by ID algorithm
11 / 13

12. Conclusions
We have developed a sound a complete algorithm for
identification of Dynamic Causal Networks
DCN-ID algorithm valid for DCNs with static, dynamic
confounders
DCNs do not need to be time-invariant
However our algorithm reveals some properties of
time-invariant DCNs:
1) DCNs with static confounders recover time invariant
behaviour after intervention
2) DCNs with dynamic confounders do not recover
time-invariant behaviour after the intervention
12 / 13

13. Identifiability in Dynamic Causal Networks
Gilles Blondel, Marta Arias, Ricard Gavaldà
Universitat Politècnica de Catalunya, Barcelona
4th Graph-TA, Barcelona, March 2016
Contact: gblondel@cs.upc.edu
13 / 13