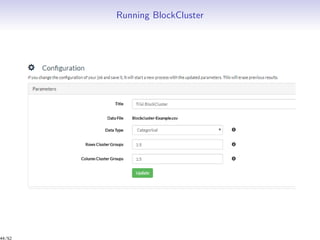
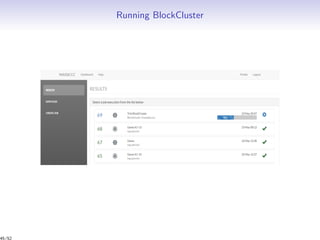
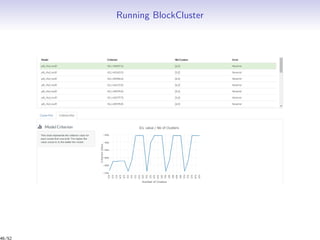
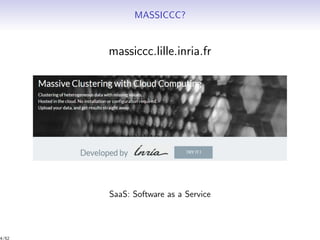
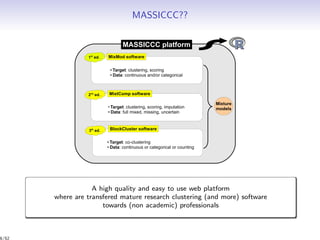
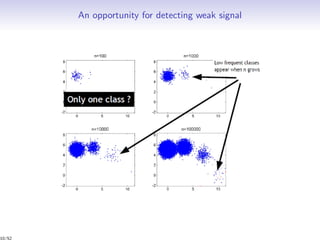
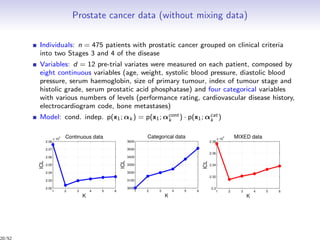
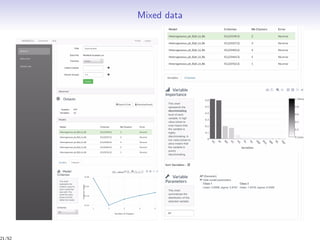
Massiccc is a software as a service (SaaS) platform designed for clustering and co-clustering of mixed data, catering to professionals and applications across various sectors such as predictive maintenance and health data mining. It offers advanced clustering techniques for dealing with complex datasets that include continuous, categorical, and missing data through various software modules like mixmod and mixtcomp. The platform aims to provide a user-friendly interface for analyzing large and intricate data sets while ensuring high-quality clustering results.

1. 1/52

2. MASSICCC: A SaaS Platform for
Clustering and Co-Clustering of Mixed Data
https://massiccc.lille.inria.fr/
F. Laporte
with B. Auder, C. Biernacki, G. Celeux, J. Demont, F. Langrognet, V. Kubicki, C. Poli, J. Renault, S. Iovleff
May 29th 2019, TechTalk, Paris
2/52

3. Outline
1 Introduction
2 Model-based clustering
3 Mixmod in MASSICCC
4 MixtComp in MASSICCC
5 BlockCluster in MASSICCC
6 Conclusion
3/52

4. MASSICCC?
massiccc.lille.inria.fr
SaaS: Software as a Service
4/52

5. MASSICCC: Examples of Applications
Market sales
Cities’ similarities
Predictive maintenance
Health
Data mining
Large dataset
Complex dataset
5/52

6. MASSICCC??
A high quality and easy to use web platform
where are transfered mature research clustering (and more) software
towards (non academic) professionals
6/52

7. Here is the computer you need!
7/52

8. Clustering?
Detect hidden structures in data sets
−1 −0.5 0 0.5 1 1.5 2 2.5
−1.5
−1
−0.5
0
0.5
1
1.5
1st MCA axis
2ndMCAaxis
−1 −0.5 0 0.5 1 1.5 2 2.5
−1.5
−1
−0.5
0
0.5
1
1.5
1st MCA axis
2ndMCAaxis
Low income
Average income
High income
8/52

9. Large data sets1
1
S. Alelyani, J. Tang and H. Liu (2013). Feature Selection for Clustering: A Review. Data Clustering:
Algorithms and Applications, 29
9/52

10. An opportunity for detecting weak signal
10/52

11. Todays features: full mixed/missing
11/52

12. Notations
Data: n individuals: x = {x1, . . . , xn} = {xO , xM } in a space X of dimension d
Observed individuals xO
Missing individuals xM
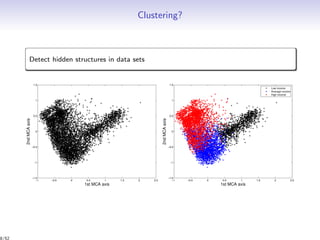
Aim: estimation of the partition z and the number of clusters K
Partition in K clusters G1, . . . , GK : z = (z1, . . . , zn), zi = (zi1, . . . , ziK )
xi ∈ Gk ⇔ zih = I{h=k}
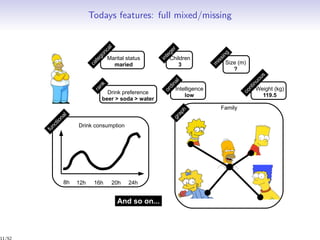
Mixed, missing, uncertain
Individuals x Partition z ⇔ Group
? 0.5 red 5 ? ? ? ⇔ ???
0.3 0.1 green 3 ? ? ? ⇔ ???
0.3 0.6 {red,green} 3 ? ? ? ⇔ ???
0.9 [0.25 0.45] red ? ? ? ? ⇔ ???
↓ ↓ ↓ ↓
continuous continuous categorical integer
12/52

13. Outline
1 Introduction
2 Model-based clustering
3 Mixmod in MASSICCC
4 MixtComp in MASSICCC
5 BlockCluster in MASSICCC
6 Conclusion
13/52

14. Parametric mixture model
Parametric assumption:
pk (x1) = p(x1; αk )
thus
p(x1) = p(x1; θ) =
K
k=1
πk p(x1; αk )
Mixture parameter:
θ = (π, α) with α = (α1, . . . , αK )
Model: it includes both the family p(·; αk ) and the number of groups K
m = {p(x1; θ) : θ ∈ Θ}
The number of free continuous parameters is given by
ν = dim(Θ)
Clustering becomes a well-posed problem. . .
14/52

15. The clustering process in mixtures
1 Estimation of θ by ˆθ
2 Estimation of the conditional probability that xi ∈ Gk
tik (ˆθ) = p(Zik = 1|Xi = xi ; ˆθ) =
ˆπk p(xi ; ˆαk )
p(xi ; ˆθ)
3 Estimation of zi by maximum a posteriori (MAP)
ˆzik = I{k=arg maxh=1,...,K tih( ˆθ)}
4 Model selection: BIC, ICL, . . .
15/52

16. Outline
1 Introduction
2 Model-based clustering
3 Mixmod in MASSICCC
4 MixtComp in MASSICCC
5 BlockCluster in MASSICCC
6 Conclusion
16/52

17. Possible datasets
Continuous data
14 models on correlation matrix between variables (models’ selection)
Categorical data
Conditional independence
Mixed data
Conditional independence inter-type
Conditional independence intra-type (symmetry between types)
Distributions
Continuous: Gaussian
Categorical: Multinomial
17/52

18. Estimation of θ
Maximize the complete-likelihood over (θ, z)
c (θ; x, z) =
n
i=1
K
k=1
zik ln {πk p(xi ; αk )} CEM
Maximize the observe-likelihood on θ
(θ; x) =
n
i=1
ln p(xi ; θ) EM
18/52

19. Principle of EM and CEM
Initialization: θ0
Iteration noq:
Step E: estimate probabilities tq
= {tik (θq
)}
Step C: classify by setting tq
= MAP({tik (θq
)})
Step M: maximize θq+1
= arg maxθ c (θ; x, tq
)
Stopping rule: iteration number or criterion stability
Properties
⊕: simplicity, monotony, low memory requirement
: local maxima (depends on θ0), linear convergence (EM)
19/52

20. Prostate cancer data (without mixing data)
Individuals: n = 475 patients with prostatic cancer grouped on clinical criteria
into two Stages 3 and 4 of the disease
Variables: d = 12 pre-trial variates were measured on each patient, composed by
eight continuous variables (age, weight, systolic blood pressure, diastolic blood
pressure, serum haemoglobin, size of primary tumour, index of tumour stage and
histolic grade, serum prostatic acid phosphatase) and four categorical variables
with various numbers of levels (performance rating, cardiovascular disease history,
electrocardiogram code, bone metastases)
Model: cond. indep. p(x1; αk ) = p(x1; αcont
k ) · p(x1; αcat
k )
20/52

21. Mixed data
21/52

22. Why should I use mixmod?
Avdantage(s)
Compare a lot of different models (continuous data)
Analyse mixed data
Disadvantage(s)
Do not handle missing data
Only continuous or categorical data
22/52

23. Outline
1 Introduction
2 Model-based clustering
3 Mixmod in MASSICCC
4 MixtComp in MASSICCC
5 BlockCluster in MASSICCC
6 Conclusion
23/52

24. Full mixed data: conditional independence everywhere2
The aim is to combine continuous, categorical, integer data, ordinal, ranking and
functional data
x1 = (xcont
1 , xcat
1 , xint
1 , . . .)
The proposed solution is to mixed all types by inter-type conditional independence
p(x1; αk ) = p(xcont
1 ; αcont
k ) × p(xcat
1 ; αcat
k ) × p(xint
1 ; αint
k ) × . . .
In addition, for symmetry between types, intra-type conditional independence
Only need to define the univariate pdf for each variable type!
Continuous: Gaussian
Categorical: multinomial
Integer: Poisson
. . .
2
MixtComp software on the MASSICCC platform: https://massiccc.lille.inria.fr/
24/52

25. Missing data: MAR assumption and estimation
Assumption on the missingness mecanism
Missing At Randon (MAR): the probability that a variable is missing does not
depend on its own value given the observed variables.
Observed log-likelihood. . .
(θ; xO
) =
n
i=1
log
K
k=1
πk p(xO
i ; αk ) =
n
i=1
log






K
k=1
πk
xM
i
p(xO
i , xM
i ; αk)dxM
i
MAR assumption






25/52

26. SEM algorithm3
A SEM algorithm to estimate θ by maximizing the observed-data log-likelihood
Initialisation: θ(0)
Iteration nb q:
E-step: compute conditional probabilities p(xM
, z|x0
; θ(q)
)
S-step: draw (xM(q)
, z(q)
) from p(xM
, z|x0
; θ(q)
)
M-step: maximize θ(q+1)
= arg maxθ ln p(xO
, xM(q)
, z(q)
; θ)
Stopping rule: iteration number
Properties: simpler than EM and interesting properties!
Avoid possibly difficult E-step in an EM
Classical M steps
Avoids local maxima
The mean of the sequence (θ(q)) approximates ˆθ
The variance of the sequence (θ(q)) gives confidence intervals
3
MixtComp software on the MASSICCC platform: https://massiccc.lille.inria.fr/
26/52

27. Prostate cancer data (with missing data)4
Individuals: 506 patients with prostatic cancer grouped on clinical criteria into
two Stages 3 and 4 of the disease
Variables: d = 12 pre-trial variates were measured on each patient, composed by
eight continuous variables (age, weight, systolic blood pressure, diastolic blood
pressure, serum haemoglobin, size of primary tumour, index of tumour stage and
histolic grade, serum prostatic acid phosphatase) and four categorical variables
with various numbers of levels (performance rating, cardiovascular disease history,
electrocardiogram code, bone metastases)
Some missing data: 62 missing values (≈ 1%)
We forget the classes (Stages of the desease) for performing clustering
Questions
How many clusters?
Which partition?
4
Byar DP, Green SB (1980): Bulletin Cancer, Paris 67:477-488
27/52

28. Data upload without preprocessing
28/52

29. Run clustering analysis
29/52

30. Several quick result overviews. . . without post-processing
30/52

31. Variable significance on global partition
+ similarity between variables
31/52

32. Variable “SG” difference between clusters
32/52

33. Variable “BM” difference between clusters
33/52

34. Companies and MixtComp
Modal (Rougegorge)
Inriatech (Alstom, ArcelorMittal, D´ecathlon, ...)
DiagRAMS technologies (predictive maintenance)
34/52

35. Why should I use MixtComp?
Avdantage(s)
Analyse different kinds of data
Handle missing and partially missing data
Disadvantage(s)
Do not use correlation structure (even with continuous data)
35/52

36. Outline
1 Introduction
2 Model-based clustering
3 Mixmod in MASSICCC
4 MixtComp in MASSICCC
5 BlockCluster in MASSICCC
6 Conclusion
36/52

37. High-dimensional (HD) data5
5
S. Alelyani, J. Tang and H. Liu (2013). Feature Selection for Clustering: A Review. Data Clustering:
Algorithms and Applications, 29
37/52

38. From clustering to co-clustering
[Govaert, 2011]
38/52

39. Notations
zi : the cluster of the row i
wj : the cluster of the column j
(zi , wj ): the block of the element xij (row i, column j)
z = (z1, . . . , zn): partition of individuals in K custers of rows
w = (w1, . . . , wd ): partition of variables in L clusters of columns
(z, w): bi-partition of the whole data set x
Both space partitions are respectively denoted by Z and W
Restriction
All variables are of the same kind (research in progress for overcoming that. . . )
39/52

40. MLE estimation: EM algorithm
Observed log-likelihood: (θ; x) = log p(x; θ)
Complete log-likelihood:
c (θ; x, z, w) = log p(x, z, w; θ)
=
i,k
zik log πk +
k,l
wjl log ρl +
i,j,k,l
zik wjl log p(xj
i ; αkl )
E-step of EM (iteration q):
Q(θ, θ(q)
) = E[ c (θ; x, z, w)|x; θ(q)
]
=
i,k
p(zi = k|x; θ(q)
)
t
(q)
ik
ln πk +
j,l
p(wi = l|x; θ(q)
)
s
(q)
jl
ln ρl
+
i,j,k,l
p(zi = k, wj = l|x; θ(q)
)
e
(q)
ijkl
ln p(xij ; αkl )
M-step of EM (iteration q): classical. For instance, for the Bernoulli case, it gives
π
(q+1)
k = i t
(q)
ik
n
, ρ
(q+1)
l =
j s
(q)
jl
d
, α
(q+1)
kl =
i,j e
(q)
ijkl xij
i,j e
(q)
ijkl
40/52

41. MLE: intractable E step
e
(q)
ijkl is usually intractable. . .
Consequence of dependency between xij s (link between rows and columns)
Involve KnLd calculus (number of possible blocks)
Example: if n = d = 20 and K = L = 2 then 1012 blocks
Example (cont’d): 33 years with a computer calculating 100,000 blocks/second
Alternatives to EM
Variational EM (numerical approx.): conditional independence assumption
p(z, w|x; θ) ≈ p(z|x; θ)p(w|x; θ)
SEM-Gibbs (stochastic approx.): replace E-step by a S-step approx. by Gibbs
z|x, w; θ and w|x, z; θ
41/52

42. Document clustering (1/2)
Mixture of 1033 medical summaries and 1398 aeronautics summaries
Lines: 2431 documents
Columns: present words (except stop), thus 9275 unique words
Data matrix: cross counting document×words
Poisson model
42/52

43. Document clustering (2/2)
Results with 2×2 blocs
Medline Cranfield
Medline 1033 0
Cranfield 0 1398
43/52

44. Running BlockCluster
44/52

45. Running BlockCluster
45/52

46. Running BlockCluster
46/52

47. Running BlockCluster
47/52

48. Why should I use BlockCluster?
Advantage(s)
Co-clustering (HD data)
Disadvantage(s)
Analyse one kind of data at a time
48/52

49. Outline
1 Introduction
2 Model-based clustering
3 Mixmod in MASSICCC
4 MixtComp in MASSICCC
5 BlockCluster in MASSICCC
6 Conclusion
49/52

50. Current work
mixmod
Missing Not At Random data (using logit distribution) =⇒ missing values
impact the probability of missingness
Patnership between CMAP/INRIA/Traumabase
Work with C. Biernacki, G. Celeux, J. Josse and Y. Stroppa
MixtComp
Publish an R package on CRAN
With you?
New kind of data
Complex missingness
2D clusters’ plot
50/52

51. Use probabilistic modelling as a mathematical guideline
Use the MASSICCC platform for user-friendly implementation
User-friendly interpretation
”One for all” of clustering
Low computer requirement needed
Free software
https://massiccc.lille.inria.fr/
Also check R packages (https://cran.r-project.org/)
Rmixmod: https://cran.r-project.org/web/packages/Rmixmod/index.html
blockcluster: https://cran.r-project.org/web/packages/blockcluster/index.html
51/52

52. MERCI
!
52/52