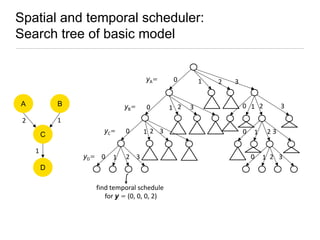
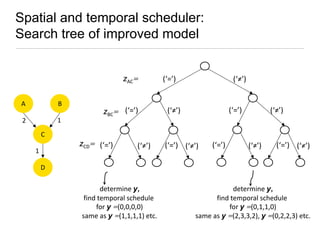
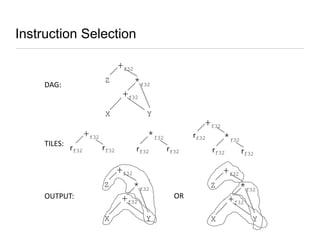
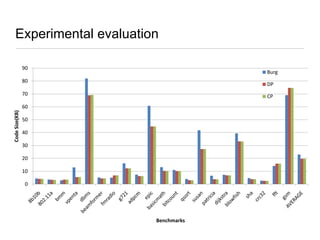
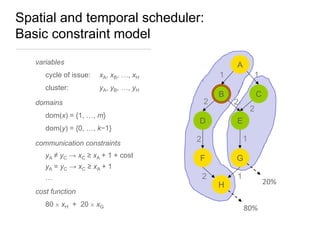
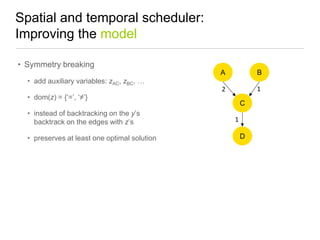
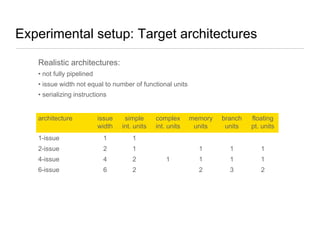
Constraint programming techniques were applied to compiler optimization problems like instruction selection, instruction scheduling, and register allocation. The techniques were able to find optimal solutions to some problems that were previously only solved heuristically. Constraint models were improved over time by adding implied constraints, dominance constraints, and preprocessing. Solvers were improved through techniques like restarts, portfolios, and machine learning of heuristics. The approach led to identifying and solving interesting subproblems with general applicability, like improved consistency algorithms for global constraints.

1. Constraint Programming in Compiler
Optimization: Lessons Learned
Peter van Beek
University of Waterloo

2. Acknowledgements
• Joint work with:
• Funding:
Omer Beg
NSERC
Alejandro López-Ortiz
IBM Canada
Abid Malik
Jim McInnes
Wayne Oldford
Claude-Guy Quimper
John Tromp
Kent Wilken
Huayue Wu

3. Application-driven research
• Idea:
• pick an application—a real-world problem—where, if you solve it, there would be a
significant impact
• Along the way, if all goes well, you will also:
• identify and fill gaps in theory
• identify and solve interesting sub-problems whose solutions will have general
applicability

4. Optimization problems in compilers
• Instruction selection
• Instruction scheduling
• basic-block scheduling
• super-block scheduling
• loop scheduling: tiling, unrolling, fusion
• Memory hierarchy optimizations
• Register allocation

5. Optimization problems in compilers
• Instruction selection
• Instruction scheduling
• basic-block scheduling
• super-block scheduling
• loop scheduling: tiling, unrolling, fusion
• Memory hierarchy optimizations
• Register allocation

6. Production compilers
“At the outset, note that basic-block scheduling is an NP-hard
problem, even with a very simple formulation of the
problem, so we must seek an effective heuristic, rather than an
exact approach.”
Steven Muchnick,
Advanced Compiler Design
& Implementation, 1997

7. Outline
• Introduction
• computer architecture
• superblock scheduling
• Constraint programming approach
• temporal scheduler
• spatial and temporal scheduler
• Experiments
• experimental setup
• experimental results
• Lessons learned

8. Computer architecture:
Performing instructions in parallel
• Multiple-issue
• multiple functional units;
e.g., ALUs, FPUs, load/store units, branch
units
• multiple instructions can be issued (begin
execution) each clock cycle
• issue width: max number of instructions that
can be issued each clock cycle
• on most architectures issue width less than
number of functional units

9. Computer architecture:
Performing instructions in parallel
• Pipelining
• overlap execution of instructions on a single
functional unit
• latency of an instruction
number of cycles before result is available
• execution time of an instruction
number of cycles before next instruction
can be issued on same functional unit
• serializing instruction
instruction that requires exclusive use of
entire processor in cycle in which it is issued
Analogy: vehicle assembly line

10. Superblock instruction scheduling
• Instruction scheduling
• assignment of a clock cycle to each instruction
• needed to take advantage of complex features of
architecture
• sometimes necessary for correctness (VLIW)
• Basic block
• straight-line sequence of code with single entry, single exit
• Superblock
• collection of basic blocks with a unique entrance but multiple exits
• Given a target architecture, find schedule with minimum expected
completion time

11. Example superblock
A:1
1
dependency DAG
• nodes
1
C:1
B:3
5
5
• one for each instruction
• labeled with execution time
D:1
2
• nodes F and G are branch
instructions, labeled with
probability the exit is taken
0
0
2
F:1
• arcs
• represent precedence
E:1
0
40%
G:1
• labeled with latencies
60%

12. Example superblock
A:1
1
optimal cost schedule for
2-issue processor
cycle
C:1
B:3
5
5
ALU FPU
1
2
D:1
A
B
E:1
2
3
4
5
1
0
2
F:1
C
0
6
7
8
E
0
D
9
G:1
F
10
40%
G
60%

13. Computer architecture:
General purpose architectures
processor
f
register file
i
b
m

14. Computer architecture:
Clustered architectures
cluster 1
cluster 2
f1
i1
b1
f2
m1
i2
b2
m2
c1
c2
register
file
register
file
cluster
interconnect
c0
c3
register
file
register
file
f0
cluster 0
i0
b0
m0
f3
i3
b3
m3
cluster 3

15. Computer architecture:
Clustered architectures
• Current: digital signal processing
• multimedia, audio processing, image processing
• wireless, ADSL modems, …
• Future trend: general purpose multi-core processors
• large numbers of cores
• fast inter-processor communication

16. Spatial and temporal scheduling
A
1
2
1
B
C
2
D
cycle
2
E
1
2
F
G
2
1
20%
H
1
2
3
4
5
6
7
8
9
10
c0
cycle
A
B
C
D
E
F
G
H
cost = 9.8
80%
1
2
3
4
5
6
7
8
9
10
c0
c1
A
B
C
D
E
F
G
H
cost = 7.6

17. Spatial and temporal scheduling
A
1
2
1
B
C
2
D
cycle
2
E
1
2
F
G
2
1
20%
H
1
2
3
4
5
6
7
8
9
10
c0
c1
A
B
C
D
E
F
G
H
cost = 7.6
80%

18. Approaches
• Superblock instruction scheduling is NP-complete
• Heuristic approaches in all commercial and open-source research compilers
• greedy list scheduling algorithm coupled with a priority heuristic
• Here: Optimal approach
• useful when longer compile times are tolerable
• e.g., compiling for software libraries, digital signal processing, embedded
applications, final production build

19. Outline
• Introduction
• computer architecture
• superblock scheduling
• Constraint programming approach
• temporal scheduler
• spatial and temporal scheduler
• Experiments
• experimental setup
• experimental results
• Lessons learned

20. Temporal scheduler:
Basic constraint model
A
1
variables
1
C
B
A, B, C, D, E, F, G
5
5
domains
{1, …, m}
D
constraints
E
2
B
A + 1, C
D
B + 5, …, G
0
0
A + 1,
F
2
F
gcc(A, B, C, F, G, nALU)
gcc(D, E, nFPU)
gcc(A, …, G, issuewidth)
0
40%
G
cost function
40 F + 60 G
60%

21. Temporal scheduler
Basic constraint model (con‟t)
non-fully pipelined instructions
• introduce auxiliary variables
PB,1
PB,2
• introduce additional constraints
B + 1 = PB,1
B + 2 = PB,2
gcc(A, B, PB,1, PB,2 C, F, G, nALU)
serializing instructions
• similar technique
B:3

22. Temporal scheduler:
Improving the model
• Add constraints to increase constraint propagation (e.g., Smith 2006)
• implied constraints: do not change set of solutions
• dominance constraints: preserve an optimal solution
• Here:
• many constraints added to constraint model in extensive preprocessing stage
that occurs once
• extensive preprocessing effort pays off as model is solved many times

23. Temporal scheduler:
Improving the solver
• From optimization to satisfaction
• find bounds on cost function
• enumerate solutions to cost function (knapsack constraint; Trick 2001)
• step through in increasing order of cost
• Improved bounds consistency algorithm for gcc constraints
• Use portfolio to improve performance (Gomes et al. 1997)
• increasing levels of constraint propagation
• Impact-based variable ordering (Refalo 2004)
• Structure-based decomposition technique (Freuder 1994)

24. Spatial and temporal scheduler:
Basic constraint model
variables
A
cycle of issue:
xA, xB, …, xH
cluster:
yA, yB, …, yH
1
2
domains
dom(x) = {1, …, m}
dom(y) = {0, …, k−1}
communication constraints
yA ≠ yC → xC ≥ xA + 1 + cost
B
C
2
D
2
E
1
2
…
G
1
20%
H
cost function
xH + 20
F
2
yA = yC → xC ≥ xA + 1
80
1
xG
80%

25. Spatial and temporal scheduler:
Improving the model
• Symmetry breaking
A
• add auxiliary variables: zAC, zBC, …
• dom(z) = {„=‟, „≠‟}
• instead of backtracking on the y‟s
backtrack on the edges with z‟s
• preserves at least one optimal solution
B
2
1
C
1
D

26. Spatial and temporal scheduler:
Improving the solver
• Preprocess DAG to find instructions which must be on same cluster
• preserve an optimal solution
• Variable ordering
• assign z variables first, in breadth-first order of DAG
• determine assignment for corresponding y variables
• determine cost of temporal schedule for these assignments

27. Outline
• Introduction
• computer architecture
• superblock scheduling
• Constraint programming approach
• temporal scheduler
• spatial and temporal scheduler
• Experiments
• experimental setup
• experimental results
• Lessons learned

28. Experimental setup: Instances
• All 154,651 superblocks from SPEC 2000 integer and floating pt. benchmarks
• standard benchmark suite
• consists of software packages chosen to be representative of types of
programming languages and applications
• superblocks generated by IBM‟s Tobey compiler when compiling the software
packages
• compilations done using Tobey‟s highest level of optimization

29. Experimental setup: Target architectures
Realistic architectures:
• not fully pipelined
• issue width not equal to number of functional units
• serializing instructions
architecture
issue
width
simple
int. units
1-issue
1
1
2-issue
2
1
4-issue
4
2
6-issue
6
2
complex
int. units
branch
units
floating
pt. units
1
1
memory
units
1
1
1
1
1
2
3
2

30. Experimental results: Temporal scheduler
Total time (hh:mm:ss) to schedule all superblocks and percentage
solved to optimality, for various time limits for solving each instance
1 sec.
architecture
time
10 sec.
%
time
1 min.
%
7:15:46 99.38
time
10 min.
%
10:22:36 99.96
time
%
1-issue
1:30:20 97.34
15:08:44 99.98
2-issue
3:57:13 91.83 30:53:83 93.90 108:50:01 97.18 665:31:00 97.70
4-issue
2:17:44 95.47 17:09:48 96.60
61:29:31 98.43 343:04:46 98.87
6-issue
3:04:18 93.59 25:03:44 94.76
87:04:34 97.78 511:19:14 98.29

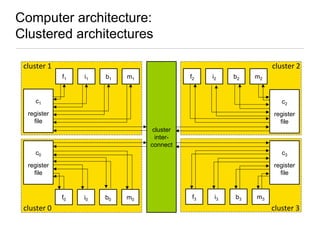
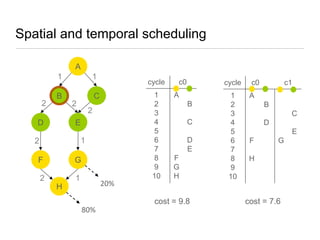
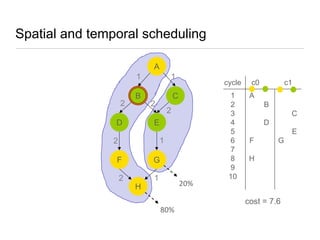
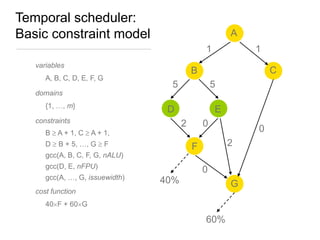
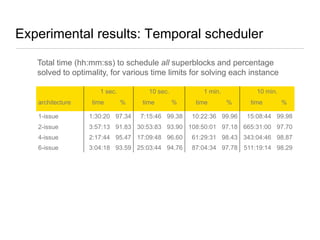
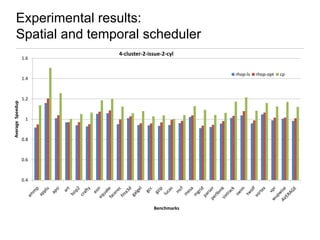
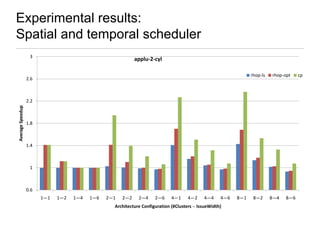
31. Spatial and temporal scheduler:
Some related work
• Bottom Up Greedy (BUG) [Ellis. MIT Press „86]
• greedy heuristic algorithm
• localized clustering decisions
• Hierarchical Partitioning (RHOP) [Chu et al. PLDI „03]
• coarsening and refinement heuristic
• weights of nodes and edges updated as algorithm progresses

32. Experimental results:
Spatial and temporal scheduler
1.6
4-cluster-2-issue-2-cyl
rhop-ls
Average Speedup
1.4
1.2
1
0.8
0.6
0.4
Benchmarks
rhop-opt
cp

33. Experimental results:
Spatial and temporal scheduler
3
applu-2-cyl
rhop-ls
2.6
rhop-opt
Average Speedup
2.2
1.8
1.4
1
0.6
1―1
1―2
1―4
1―6
2―1
2―2
2―4
2―6
4―1
4―2
4―4
4―6
Architecture Configuration (#Clusters – IssueWidth)
8―1
8―2
8―4
8―6
cp

34. Outline
• Introduction
• computer architecture
• superblock scheduling
• Constraint programming approach
• temporal scheduler
• spatial and temporal scheduler
• Experiments
• experimental setup
• experimental results
• Lessons learned

35. Lessons learned (I)
• Pick problem carefully
• is a new solution needed?
• what is the likelihood of success?
• Existing heuristics may not leave any room for improvement
• examples: basic block scheduling, instruction selection

36. Lessons learned (II)
• Be prepared for adversity
• significant overhead
• learning domain of application
• significant implementation
• significant engineering
• different research cultures
• researchers are tribal
• different standards of reviewing (number & contentiousness)
• different standards of evaluation, formalization, assumptions

37. Lessons learned (III)
• Rewards
• can be attractive to students
• can lead to identifying and solving interesting sub-problems whose solutions have
general applicability
• bounds consistency for alldifferent and gcc global constraints
• restarts and portfolios
• machine learning of heuristics

38. Optimization problems in compilers
• Instruction selection
• Instruction scheduling
• basic-block scheduling
• super-block scheduling
• loop scheduling: tiling, unrolling, fusion
• Memory hierarchy optimizations
• Register allocation

39. Selected publications
• Applications
A. M. Malik, M. Chase, T. Russell, and P. van Beek. An application of constraint programming to superblock
instruction scheduling. CP-2008.
M. Beg and P. van Beek. A constraint programming approach for integrated spatial and temporal scheduling for
clustered architectures. ACM TECS, To appear.
• Global constraints
C.-G. Quimper, P. van Beek, A. Lopez-Ortiz, A. Golynski, and S. Bashir Sadjad. An efficient bounds consistency
algorithm for the global cardinality constraint. CP-2003.
A. Lopez-Ortiz, C.-G. Quimper, J. Tromp, and P. van Beek. A fast and simple algorithm for bounds consistency of
the alldifferent constraint. IJCAI-2003.
• Portfolios and restarts
H. Wu and P. van Beek. On portfolios for backtracking search in the presence of deadlines. ICTAI-2007.
H. Wu and P. van Beek. On universal restart strategies for backtracking search. CP-2007.
• Heuristics and machine learning
T. Russell, A. M. Malik, M. Chase, and P. van Beek. Learning heuristics for the superblock instruction scheduling
problem. IEEE TKDE, 2009.
M. Chase, A. M. Malik, T. Russell, R. W. Oldford, and P. van Beek. A computational study of heuristic and exact
techniques for superblock instruction scheduling. J. of Scheduling, 2012.

40. Next project:
Smart water infrastructure / water analytics

41. Spatial and temporal scheduler:
Search tree of basic model
yA=
A
B
2
0
1
2
3
1
yB=
yC=
C
1
yD=
0
1
0
0
12 3
2 3
D
find temporal schedule
for y = (0, 0, 0, 2)
1 2
3
0 1 2
0
1
0
3
23
1 2 3

42. Spatial and temporal scheduler:
Search tree of improved model
zAC=
A
B
2
1
C
1
zBC= (‘=’)
zCD= (‘=’)
(‘≠’)
(‘=’)
(‘≠’)
(‘=’)
(‘≠’)
(‘=’) (‘≠’)
(‘=’)
(‘≠’)
(‘≠’)
(‘=’) (‘≠’)
D
determine y,
find temporal schedule
for y =(0,0,0,0)
same as y =(1,1,1,1) etc.
determine y,
find temporal schedule
for y =(0,1,1,0)
same as y =(2,3,3,2), y =(0,2,2,3) etc.

43. Instruction Selection
+f32
*f32
Z
DAG:
+f32
Y
X
+f32
TILES:
rf32
+f32
*f32
rf32
rf32
*f32
rf32
rf32
rf32
+f32
Z
OUTPUT:
+f32
*f32
Z
OR
+f32
X
rf32
Y
*f32
+f32
X
Y

44. Instruction Selection
• Given
• an expression DAG G
• a set of tiles representing machine instructions
• Find a mapping of tiles to nodes in G of minimal cost (size) that covers G
• Complexity:
• polynomial for trees
• NP-hard for DAGs

45. Experimental evaluation
90
Burg
80
DP
70
CP
Code Size(KB)
60
50
40
30
20
10
0
Benchmarks