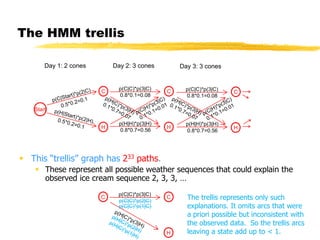
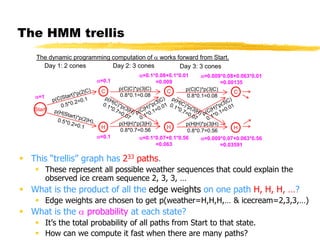
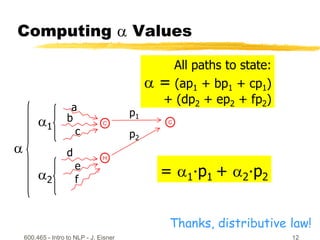
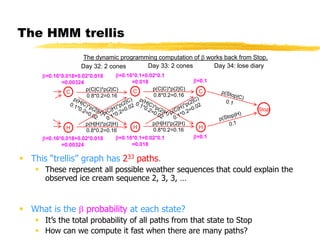
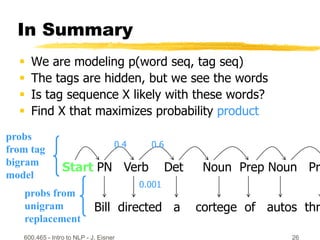
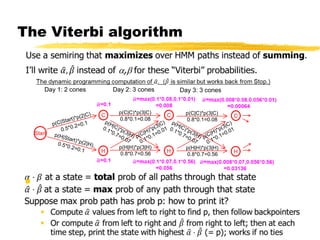
This document discusses hidden Markov models and the forward-backward algorithm. It introduces marginalization and conditionalization concepts using sales data examples. It then explains how these concepts apply to a weather prediction example modeled as a hidden Markov model. The document discusses computing alpha and beta values using the forward-backward algorithm to find the most likely hidden state sequence. It also discusses how hidden Markov models can be used for part-of-speech tagging of text.