This document provides an overview of logical approaches to analyzing the security of distributed systems. It discusses cryptographic protocols, web services, and modeling tools. The document is divided into three sections. The first section describes cryptographic protocols and web services. The second section discusses tools for modeling these systems using first-order logic. The third section presents symbolic models for cryptographic protocols and a proposed model for analyzing web services security.









![10 CHAPTER 1. INTRODUCTION
have been performed, the logical consequence problem is decidable. This re-
sult is based on a refinement of resolution based on an ordering in which every
atom without variables is greater than only a bounded number of other atoms.
This presentation is followed by its (unpublished) extension to well-founded
orderings I have obtained with Mounira Kourjieh when solving cryptographic
protocol analysis problems.
Modelling. Now that the reader is equipped with a “survival toolkit” in first-
order logic I present the formal models on which the analysis is performed.
Chapter 6 includes an article written in collaboration with M. Rusinowitch on
the compilation of standard cryptographic protocol specifications into active
frames. These are a simplified formal model of protocol participants in which
only the global effects, not the individual operations, of the participant are taken
into account. Also in this chapter I introduce symbolic derivations in which all
operations must be atomic. In contrast with active frames, which have an in-
tuitive semantics, and with process calculi, that rely on standard programming
constructions, symbolic derivations are designed to ease the reasoning on pro-
tocol participants and on the intruder, at the cost of a difficulty to relate this
model of computation to standard constructions.
In contrast with cryptographic protocols in which entities usually terminate
their participation to the protocol after a few execution steps, Web Services
may exhibit a rich behavior. Trust negotiation in particular usually ends once a
fixpoint is reached. Thus in order to take into account the access control part of
the Web Service specifications we need to consider a framework in which loops
are allowed. In collaboration with Philippe Balbiani and Marwa ElHouri I have
proposed one such framework in [21, 22], from which Chapter 7 is extracted.
Results obtained. The last part of this document presents the decidability
or combination results I have obtained since I obtained my Ph.D. In a first
chapter I present a synthesis of several results obtained around the decidability
of the insecurity problem of cryptographic protocols when only a finite number of
message exchanges by honest agents are allowed. Instead of focusing on each of
the settings considered, I have tried to how these different results are connected
one with another. In doing so I have assumed that the reader is already familiar
with the proofs and techniques employed in the articles [61, 67, 62].
Then in Chapter 9 I present the results obtained while I was invited in the
Cassis project at INRIA Nancy Grand Est. I have worked there in collaboration
with M. Rusinowitch, M. Turuani, and with two Ph.D. students, Mohammed
Anis Mekki and Tigran Avanesov. We have worked on the application of the
techniques developped primarily for cryptographic protocol analysis to solve ba-
sic orchestration problems, which are both special reachability problems. With
M.A. Mekki the study was focused on building a complete tool that takes in its
input a description of the available services in an Alice&Bob-like notation and
a description of the goal of the orchestration, and produces a deployment-ready
validated orchestrator service. At the time of writing, that service is deployed](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-10-320.jpg)
![1.3. DOCUMENT OUTLINE 11
as a tomcat servlet, but all the cryptography is implemented within the body
of the SOAP messages. With T. Avanesov we have considered a multi-intruder
extension of the standard cryptographic protocol analysis setting. When per-
forming security analysis, this setting permits us to model situations in which
several intruders are willing to collaborate one with another, but cannot com-
municate directly, and thus have to pass the information they want to exchange
through honest agents. When composing Web Services, we look at a distributed
orchestration problem: several partners are willing to collaborate, but they do
not wish to share all the information they have. The problem then is to decide
whether the participants’ security policies are flexible enough to allow them
to collectively implement the goal service. Generally speaking, this problem
is strictly more difficult than standard orchestration (or cryptographic protocol
analysis) given that in addition to a decision procedure for the case of Dolev-Yao
like message manipulations, we have obtained an undecidability result when the
equational theory that defines the operations is subterm and convergent.
Finally in Chapter 10 I present some work on the equivalence of symbolic
derivations. The problem is to determine whether an intruder can observe dif-
ferences in the execution of two different protocols. A preliminary result ob-
tained in collaboration with M. Rusinowitch was published in [75]. In that
paper we have provided a more succinct proof of the decidability of this prob-
lem for subterm convergent equational theories, a result originally obtained by
M. Baudet [27]. In this chapter I present a criterion that actually permits one
to reduce this equivalence problem to the reachability analysis performed when
considered the usual trace properties. I believe that the reduction can easily be
implemented in reachability analysis tools such as CL-AtSe or OFMC, and thus
may be of practical interest.
Epilogue. This document ends with a last chapter on the future research di-
rections stemming from the results obtained so far. A one-sentence summary
would be more of the same, but differently. While I plan to continue the work
around reachability analysis problems, I also plan to explore further the side-
ways, namely:
• to work on the potential applications to safety analysis;
• to explore further the relation between reachability analysis and first-order
automated reasoning techniques;
• to obtain a comprehensive framework for service composition that also
takes into account trust negotiation, and as a consequence to relate more
formally the models for protocols and Web Services presented in this doc-
ument;
• to extend the modularity results obtained to address the modular verifi-
cation of aspect-based programs.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-11-320.jpg)




![16 CHAPTER 2. CRYPTOGRAPHIC PROTOCOLS
The most common types are:
Secret key cryptosystems: this type of cryptography has been the only type
of cryptography until the 1970s. It relies on a secret piece of information,
called a secret key, known only within a small group. Every member of
this group can both cipher and decipher messages with the key, while
agents outside of it can neither cipher nor decipher the encoded message.
Instances of secret key cryptosystems are the Enigma [214], DES [165],
3DES [169], and the current AES [170]. Given a message M , and a secret
key sk(k) we denote:
encs (M, sk(k)):the encryption of M with the key sk(k)
decs (M, sk(k)):the decryption of M with the key sk(k)
Public key cryptosystems: the first (tentative) publication [158] on public
key cryptography was met with skepticism, as in the words of a reviewer:
“Experience shows that it is extremely dangerous to transmit key
information in the clear.” 1
The first accepted paper on the topic was the presentation by Diffie and
Hellman [104] of a clever usage of exponentiation in modular arithmetic.
The result of their analysis was the possibility to compute a couple of
keys (pk(k), sk(k)) such that the messages encrypted with the key pk(k)
can be decrypted only with the key sk(k), and such that sk(k) cannot
feasibly be computed from pk(k). Thus the key pk(k) can be published
as a phone number would be, and any participant can send information
only to the agent knowing the key sk(k), given that only that agent can
decrypt, i.e. understand. Examples of public-key cryptosystems include
RSA [186, 31, 179, 180], ElGamal [116]. Given a message M , a public key
pk(k) and a secret key sk(k) we denote:
encp (M, pk(k)) the encryption of M with the key pk(k)
decp (M, sk(k)) the decryption of M with the key sk(k)
Signature cryptosystems: the asymmetry of public key cryptosystems can
also be employed to authenticate the creator of a message. The sender
signs the message he wants to send with a secret key sk(k). Anybody
knowing the public key pk(k) can then verify that the signature was com-
posed with the key sk(k), and thus originates from the possessor of that
key. Given a message M , a public key pk(k) and a secret key sk(k) we
denote:
sign(M, sk(k)) the signature of M with the key sk(k)
verif (M , M, pk(k)) the check that M is the signature of M with
the inverse of the key pk(k)
1 http://www.merkle.com/1974/](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-16-320.jpg)
![2.1. CRYPTOGRAPHIC PROTOCOLS 17
Other functions are employed to construct messages such as the concatena-
tion M1 , M2 of two messages. We also consider the modeling of mathematics
functions such that the bitwise exclusive-or or the modular exponentiation, and
will add the corresponding symbols as necessary.
2.1.2 RFCs
Cryptographic protocols are published and endorsed by various governmental
or private organizations. These organizations can be formed to support one spe-
cific (set of) protocols, such as the “Liberty Alliance”, or have a more general
interest in one domain, such as the “Oasis Open consortium” or the “World
Wide Web Consortium”, for respectively the transmission and representation
of information in the XML format or the Web. The Internet Engineering Task
Force (IETF) is particularly important as an organization focusing on the basic
protocols employed in the computer-to-computer communications, and on the
interoperability of their implementations. Transport Layer Security [102, 103]
(TLS) is specified by a Request for Comments (RFC) document, as are some
protocol proposals in early stages, such as RFC 2945 that describes the SRP
Authentication and Key Exchange System. In the latter case implementation
issues are not discussed, but the principle of the protocol is presented. Often
such documents contain a finite state automaton describing the different states
in which a program implementing the protocol can be as well as the possible
actions in each state, and/or the intended sequence of messages between par-
ticipants in the protocol, as in Figure 2.1.
Client Host
U =<username> →
← s =<salt from passwd file>
Upon identifying himself to the host, the client will receive the
salt stored on the host under his username.
a =random()
A = g a %N →
v =<stored password verifier>
b =random()
← B = (v + g b )%N
p =<raw password>
x = SHA(s|SHA(U |” : ”|p))
S = (B − g x )(a+u∗x) %N S = (A ∗ v u )b %N
K =SHA Interleave(S) K =SHA Interleave(S)
Figure 2.1: Annotated message sequence chart extracted from the RFC 2945
(SRP Authentication and Key Exchange System)](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-17-320.jpg)
![18 CHAPTER 2. CRYPTOGRAPHIC PROTOCOLS
2.1.3 Narrations
Though in the Avispa and Avantssar we have worked on the definition of more
complex protocol specification languages, the specification of a protocol by a
single sequence of messages as in [98, 148, 126, 162] is sufficient for most cryp-
tographic protocols even though the internal computations of the agents is not
specified. In its simplest form, a narration is a sequence of message exchanges
followed by the initial knowledge each participant must have to engage in the
protocol (Needham-Schroeder Public Key protocol, [166]):
A→B:encp ( A, Na , KB )
B→A:encp ( Na , Nb , KA )
A→B:encp (Nb , KB )
where
−1
A knows A, B, KA , KB , KA
−1
B knows A, B, KA , KB , KB
The names A and B in this sequence do not refer to any particular individual
but to roles in the narration: common names instead of A and B are Client,
Server, Initiator,. . . Actual participants in an instance (also called session) of
the protocol play each one of the roles defined by the message exchange.
We note that the messages Na and Nb are not in the knowledge of A nor
of B. These are nonces, i.e. random values created at the beginning of each
instance of the protocol.
Personal work:
We present in Chapter 6 how these narrations can be given an operational
semantics. The languages we have developed in the course of the Avispa
and Avantssar projects did not need such developments given that the
modeler of a protocol in HSPSL [64] or ASLan V.2 has to specify also
the internal actions of the roles. Though it is often tedious to write such
specifications, the language aims at a greater accuracy of the protocol
model. We note that latest works such as [163] step back on this choice
and return to simpler models.
2.1.4 Security Properties
Generally speaking [83] one can distinguish two kinds of properties for programs
such as protocols:
• Properties that are defined by a set of possible executions of the protocol;
• Hyper-properties that are defined by the set of the sets of possible execu-
tions of the protocol.
Our work principally focuses on the properties of protocols such as:
• Secrecy, i.e. determining whether one of the messages exchanged can be
constructed by an attacker;](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-18-320.jpg)
![2.1. CRYPTOGRAPHIC PROTOCOLS 19
• Authentication, i.e. determining whether the principals accept only the
messages originating from the participants listed in the narration.
Example 1. The simplified [147] version of the Needham-Schroeder Public Key
protocol (NSPK) [166] exhibits vulnerabilities to both secrecy and authentica-
tion. Whereas at the end of their respective execution A and B shall be assured
to have engaged in a conversation one with another and that the nonces Na and
Nb are kept secret, Lowe [147] found the following attack:
A → I :encp ( A, Na , KI )
I(A)→ B :encp ( A, Na , KB )
B →I(A):encp ( Na , Nb , KA )
I → A :encp ( Na , Nb , KA )
A → I :encp (Nb , KI )
I(A)→ B :encp (Nb , KB )
In this attack A starts a legitimate instance of the protocol with an intruder, i.e.
a dishonest agent I. This intruder then masquerades as A—the corresponding
events are denoted I(A)—and initiates a session with B. B responds as if he
were talking to A, and ends successfully his part of the protocol. However, in
the course of his protocol instance B has accepted messages issued by I instead
of A, hence an authenticity failure. Furthermore, the nonces Na and Nb , which
are believed by B to be a common secret shared with A, are actually known by
I, hence a secrecy breach.
Personal work:
Until recently I have worked only on the security analysis of properties
such as secrecy and authentication. However in a debuting series of work
I also consider the problem of the security analysis w.r.t. the equivalence
of protocols. This notion is employed to reason about anonymity, e-voting
protocols, abstraction of a perfect primitive by a concrete one, and so on.
Chapter 10 includes these results, which are related to the refutation of
cryptographic protocols.
2.1.5 Formal methods
We have worked on the formal analysis of cryptographic protocols. This means
that given a specification such as a narration we built a logical model of the
protocol and its environment consisting in three parts describing respectively:
• the possible actions of agents behaving as prescribed by the roles in the
protocol;
• the possible actions of an attacker in the setting considered;
• the property we want to verify.
The parallel execution of roles and of the intruder is interpreted by a conjunc-
tion. Two types of logical analysis can then be performed:](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-19-320.jpg)
![20 CHAPTER 2. CRYPTOGRAPHIC PROTOCOLS
Validation: one proves that the property is logically implied by the specifica-
tions of the protocol and of the intruder;
Refutation: one constrains the logical specifications e.g. by imposing an ini-
tial state, bounds the number of possible instances of the protocol,. . . and
proves that under these restrictions the property is not logically implied
by the specifications of the protocol and of the intruder.
When failing in refuting a protocol, we can only conclude that under the con-
straints imposed there is no attack. Of course this does not mean that there is
no attack when weaker constraints, or none, are imposed. Let us review some
of the constraints routinely imposed:
Isolation: no protocol is executed concurrently with the one under scrutiny.
While unrealistic, this assumption, or some weaker version of it, is needed
given that for any protocol P one can construct a protocol P’ [132] such
that, when P’ is executed concurrently with P the attacker can discover
a secret message exchanged in P. While this result is theoretical as the
second protocol has to be constructed from the first one, such attacks also
often occur in practice [91].
In [50, 19] the isolation assumption is weakened into assuming, in some
form or another, that no other protocol executed concurrently uses the
same cryptographic data. Concerning symbolic analysis of protocols, one
can find in [163] similar assumptions employed to obtain the soundness
of the composition of transport protocols. Other similar conditions for
the sequential or parallel composability can also be found in [10, 88] and
others that can be traced back to the non-unifiability condition initially
introduced for the decidability of secrecy in [185].
Soundness: the properties of cryptographic primitives are usually [119, 115,
184] expressed by games in which an intruder, modeled by a probabilistic
Turing machine, cannot in a reasonable amount of time have a significant
gain over a toss of coin. For instance in IND-CPA games the intruder is
given a public key. He then chooses two messages m0 and m1 , and is then
presented with the encryption of either m0 or m1 . He wins the game if he
can choose m0 and m1 such that he has strictly2 more than 50% chances
of guessing the right answer.
While there are some attempts [23, 24] to directly interpret the construc-
tions on messages in terms of probability distributions, the usual lifting
of these properties into a symbolic world is problematic given that they
express what the intruder cannot do, whereas the symbolic analysis rests
on the description of what the intruder can do. We present how the trans-
lation from the concrete cryptographic setting to the symbolic world can
be justified in Subsection 2.2.2.
2 The actual condition is actually even more restrictive, and depends on the length of the
key](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-20-320.jpg)
![2.2. VALIDATION OF CRYPTOGRAPHIC PROTOCOLS 21
Bounds on the instances of the protocol: though in practice the number
of distinct agents that can engage in an unbounded number of sessions of a
cryptographic protocol is a priori unbounded, it has been proved [85] that
if there is a secrecy (resp. authentication) failure in an arbitrary (w.r.t. the
number of sessions and the agents participating in each session) instance
of the protocol then there is a secrecy (resp. authentication) failure with
the same number of sessions but only 1 (resp. 2) distinct honest agents,
in addition to the intruder, instantiating the roles of the protocol.
Furthermore Stoller [200, 201] remarked that essentially all “standard”
protocols either had a flaw found when examining a couple of sessions
or were safe. While this cannot be argued for cryptographic protocols in
general [160] this remark lead to the refutation-based methods in which
one only tries to find an attack involving a couple of distinct instances
of the protocol. We present more in details in Section 2.3 the history of
refutation with a bounded number of instances of the protocol.
2.2 Validation of Cryptographic Protocols
2.2.1 Validation in a symbolic model
Validation of cryptographic protocols is usually performed under the assumption
that the protocol is executed in isolation, this assumption being justified by the
work on the soundness w.r.t. the concrete cryptographic setting described in
Section 2.2.2. Under this isolation hypothesis, validation of a protocol amounts
to proving that for any number of parallel instances of the protocol, each instance
provides the guarantees claimed by the protocol. This problem is usually treated
by translating the descriptions of the intruder and of the honest agents into sets
of (usually Horn) clauses, and by reducing the problem of the existence of an
attack to a satisfiability problem.
This approach is successful in practice, see for example the ProVerif tool
by B. Blanchet [38], and some decision procedures were also obtained. The
satisfiability of sets of clauses in which each clause either has at most one variable
or one function symbol is decidable [84], a NEXPTIME bound is given in [194,
195]. This problem is DEXPTIME-complete if all the clauses are furthermore
Horn clauses. The class of sets of clauses was later extended to take into account
blind copy [90] while preserving decidability.
It was also extended to take into account the properties of an exclusive
or [196]. While in this article it is also proven that adding an abelian group ad-
dition operation leads to undecidability, it was implemented in ProVerif in [137],
and the decidability of some particular case, including some group protocols,
was proven.
2.2.2 Soundness w.r.t. a concrete model
Validation of a cryptographic protocol is done w.r.t. a given attacker model.
However there is no assurance that the modeled attacker is as strong as an at-
tacker who can take advantage of the precise arithmetic relations between the](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-21-320.jpg)
![22 CHAPTER 2. CRYPTOGRAPHIC PROTOCOLS
messages, the keys, and so on. For example the Pollard ρ method [182] is based
on the computation of collisions (different products having the same result) in
a finite group and speeds-up significantly the factorization of some integers. We
thus have a discrepancy between the symbolic analysis of cryptographic primi-
tives, which is conducted independently from the actual values of the messages
exchanged and the keys, and the analysis in the concrete setting in which the
attacker has access to the actual values of the messages and the keys, with
this additional information opening the possibility of additional attacks on a
protocol.
There has been a lot of work trying to relate concrete settings to symbolic
ones, starting with [177]. As demonstrated by e.g. [50] finding a good setting is a
difficult and error-prone task. However more recent works such as [19, 138, 139]
have provided sound and usable definitions and cryptographic settings. If one
agrees on the restriction on the usage of cryptographic protocols and of keys
imposed by these settings there exists a cryptographic library that hides the
concrete values of the keys by imposing the use of pointers instead of real data
and such that every useful manipulation on message can be performed by calls
to this library.
2.3 Refutation of Cryptographic Protocols
2.3.1 Advantages over validation
Validation of cryptographic protocols is undecidable even in the simplest settings
in which perfect cryptography is employed, the protocol is executed in isolation
from other protocols, and either only a finite number of distinct values are
exchanged or some typing systems ensures that the complexity of the messages
is bounded. Furthermore the soundness of a validation procedure is hard to
establish: though one can prove that in a given symbolic model there is no
attack on a protocol, this result does not necessarily translate into the validation
of a concrete version of the protocol as was described in 2.2.2.
However, when trying to refute a protocol, the translation to the concrete
level is simpler as it suffices to prove that any action performed by the attacker
in the symbolic model can be translated into an action of an attacker in the
concrete model. Also the restrictions imposed on the protocols to ensure the
decidability of their validation are usually too strong for real-life case studies.
These reasons motivated the refutation of cryptographic protocols under
constraints: instead of trying to prove that a protocol is valid one tries to dis-
cover an attack when additional constraints on the protocol are imposed. In
accordance with the observations by Stoller [200, 201] the most common con-
straint consists in: a) bounding the number of messages the honest participants
can receive; and b) forcing the participant either to accept a message or aborts
his execution of the protocol. These assumptions can be translated in terms
of processes by imposing that the honest participants are modeled by processes
without loop and in which the “else” branch of the conditional is always an](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-22-320.jpg)
![2.3. REFUTATION OF CRYPTOGRAPHIC PROTOCOLS 23
abort. Usually one further imposes that the tests in the conditional must be
(conjunctions of) positive equality tests. Another common restriction consists
in bounding the complexity of the terms representing the messages.
Under these assumptions it is possible to devise decision procedures for the
refutation of cryptographic protocols w.r.t. a model of the attacker. When
conducting such an analysis one first has to provide the reader with a message
and deduction model, and then only can one present a decision procedure w.r.t.
these models. In more details we have:
Message model: Messages are modeled by first-order terms, i.e. finite recur-
sive structures defined by the applications of some functions on terms and
by constants. The first task in protocol refutation consists in defining the
properties of these functions. For instance one should model that a bitwise
exclusive-or operation ⊕ is commutative, i.e. for every messages x and y
the equality x ⊕ y = y ⊕ x holds;
Deduction model: Then one has to model how the attacker can use messages
at his disposal to create new ones. This is usually done by assuming
that the intruder can apply (a subset of) the symbols employed to define
the messages to construct new messages. For example an asymmetric
encryption algorithm can be employed by the intruder to construct new
messages, but the sk( ), pk( ) symbols, employed to denote the public and
private keys, cannot be employed by the intruder to construct new keys;
Decision procedure: Finally one searches a decision procedure applicable to
all finite message exchanges where the messages are as defined in the first
point when attacked by an intruder having the deduction power as defined
in the second point.
Since we attempt to refute protocols the soundness of the message and de-
duction models is more important than their completeness. Forgetting some
possible equalities or deductions may lead to inconclusive analysis (stating that
no attack is found under the current hypotheses), but having unsound equal-
ities or deductions could lead to false positives, i.e. a valid protocol could be
declared as flawed.
2.3.2 Personal Work on the Refutation of Cryptographic
Protocols
During my PhD I have worked on the refutation of cryptographic protocols
when the number of messages exchanged among the honest agents is bounded.
In collaboration with Laurent Vigneron, I first extended Amadio and Lugiez’s
decision procedure [8] to take into account the case of non-atomic secret keys
and implemented it in daTac [78]. Then we have presented an abstraction of
the parallel sessions of a cryptographic protocol [77, 79] in which it is possible
to validate strong authentication, in contrast with other existing abstractions
(e.g. [41]) in which replay attacks cannot be detected. This abstraction is based](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-23-320.jpg)
![24 CHAPTER 2. CRYPTOGRAPHIC PROTOCOLS
on a saturation of the protocol rules modeled as clauses, and on the extension of
the intruder’s deduction capacities with these so-called “oracle” rules, instead
of simply checking the property in the saturated set of rules. Then, and before
I finished my PhD, I have worked with R. K¨sters, M. Rusinowitch, and M. Tu-
u
ruani on the extension of the complexity result obtained in the case of perfect
cryptography [190, 144] to the cases in which an exclusive-or [68, 61], an expo-
nential for Diffie-Hellman [69, 62], commutative asymmetric encryption [60, 62],
or oracle rules [63] were added to the standard set of intruder deduction rules.
I finally presented a lazy constraint solving procedure [56] that extends the one
in [78] to protocols in which an exclusive-or symbol appears. This procedure
was implemented in CL-AtSe [208] by M. Turuani and M. T¨ngerthal with some
u
further optimization on the exclusive-or unification algorithm [207].
This serie of results was however non-satisfactory given that there was no
result on the decidability of refutation when e.g. both an exponential and an
exclusive-or appear in the protocol. In collaboration with M. Rusinowitch we
have considered the problem of the combination of decision procedures for refu-
tation, and presented a solution [70, 76] that reduces the refutation of protocols
expressed over the union of two disjoint sets of operators and with ordering re-
strictions to problems of refutation in individual signatures with the same kind
of ordering constraints. We later extended this result to well-moded but non-
disjoint union of signatures in [71, 72]. In [11] the authors build upon the first
combination result to obtain a similar one on the combination of static equiv-
alence decision procedures, while [157, 136] obtain similar conditions for the
combination on non-disjoint signatures, and [47] extends it to take into account
some specific properties of homomorphisms. Finally let me mention that the
well-moded constraint is rather general and intuitive, given that it was defined
to model the properties of exponential w.r.t. the abelian group of its exponents,
but was also employed in [97] to model the relationship between access control
and deductions on messages in PKCS#11.
When Mounira Kourjieh began her PhD under my supervision, we started
to work on a novel research direction. As explained above, the traditional
research on the relation between concrete and symbolic models of cryptographic
primitives is based on the establishment of a set of assumptions on the use of
these primitives and on the management of the keys, and in proving that under
these assumptions one can build a complete symbolic model such that, if there
is no flaw on the symbolic level then there is no flaw on the concrete level. We
remark that:
• the approach may be too restrictive for real-life protocols, as it requires
e.g. that the keys are created and managed by a trusted entity—the
cryptographic library;
• the soundness of validation in the symbolic model is hard to establish
given that one has to account for all the possible actions of the attackers.
This is in contrast with the soundness of refutation for which one only has
to prove that the actions described in the symbolic setting are feasible in
the concrete setting.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-24-320.jpg)
![2.3. REFUTATION OF CRYPTOGRAPHIC PROTOCOLS 25
For these two reasons we have tried to model the weaknesses of the cryptographic
primitives when no assumption is made on the keys creation and management:
instead of restricting the concrete level to make it fit a symbolic model we
have instead augmented the symbolic model to take into account the known
attacks on the concrete primitives. We have achieved decidability results for
signatures in the multi-user setting [58] and the decidability3 of the refutation
for hash functions for which it is feasible to compute collisions [57]. This work
is presented in more details in Chapter 8.
3 Under the assumption that the combination result of [71] on deduction systems also holds
on extended deduction systems.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-25-320.jpg)

![Chapter 3
Web Services
As a continuation of my work on cryptographic protocols I have
begun research on Web Services when I arrived in Toulouse
in 2004. While at first they were simply viewed as crypto-
graphic protocols exchanging XML messages, this very active
area turned out to be the source of a variety of research prob-
lems related to the modeling of the access control policy and
of the workflow of Business Processes. Also of interest is the
emerging development of modular methods for the validation of
Web Services. We introduce in this chapter Web Services with
a short historical introduction, followed by a description of the
aspects of concern to my research. I conclude it with a summary
of my research on this topic.
3.1 Web Services
3.1.1 Basic services
1
The usual characterization of Web Service defines a Web Service as an appli-
cation that communicates with remote clients using the HTTP [114] transport
protocol. The principle of having applications executed on a server computer
and used by remote clients is not an original one, as was already present in Sun’s
mid-90’s motto “Network is the computer”. However the first implementations
were impractical, for several reasons:
• Sun’s proposal was to code all the applications in Java to ensure inter-
operability.
• The Corba2 framework aimed at the independence from Java, but suffered
from the choice of a binary encoding of data (which implies the difficulty
1 This historical discussion is based, among other sources, on http://www.ibm.com/
developerworks/webservices/library/ws-arc3/.
2 Common Object Request Broker Architecture.
27](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-27-320.jpg)
![28 CHAPTER 3. WEB SERVICES
for different vendors to provide interoperable solutions) and of a dedicated
transport protocol called IIOP [159] that imposes constraints on the pro-
grammer and limits interoperability to platforms understanding it;
These limitations have not prevented both Java and Corba to be successful
in a closed environment, but were too strong for the overall adoption of these
solutions for client/server communications.
Given the workforce needed to specify, standardize, and implement inter-
operatively a protocol on a variety of platform, a natural choice for the transport
protocol was to rely on an off-the-shelf widely implemented protocol. HTTP
stood out among other possibilities because a) it is an open protocol, and
b) client interfaces are already provided by existing Web browsers, and c) these
Web browsers also already support scripting languages, and d) its traffic is in
most cases not blocked by firewalls. Furthermore, when employed in combina-
tion with the TLS [102, 103] protocol it provides the basic security guarantees
of server authentication and confidentiality. One usually differentiate between
SOAP and REST Web Services. The former are based on SOAP, an application-
level transport protocol that relies on post/get HTTP verbs. In addition to
these verbs the REST Web Services also use the update/delete ones, but do
not need the extra abstraction provided by the SOAP protocol.
Another characterization of Web Services (starting from WSDL 2.0 [187]) is
the description of an available service in the Web Service Description Language.
This is a language in which the individual functionalities, called operations, are
advertised together with a description of their in- and output messages, as well
as a description of how one can connect to the service. An important point
is that for Web Services described in WSDL, HTTP is not the only possible
transport protocol. Originally WSDL [81] was designed to describe Web Services
communicating using the SOAP [120] protocol, an application-level protocol
originally running on top of HTTP. Bindings of SOAP to other protocols such
as JMS or smtp have since been defined, and with WSDL 2.0 the application-
level transport protocol is not necessarily SOAP anymore.
Example 2. The Amazon S33 (Simple Storage Service) provides users with a
storage space as well as with operations enabling the user to set an access control
policy to her files and add, view, remove files from the store. It is available both
in the REST style and in the SOAP style.
Model. In the rest of this document we consider an abstraction of Web Ser-
vices in which the exact transport protocol employed is irrelevant, assuming
that one could describe more precisely the messages whenever one wants to
consider the exact binding employed. As a result, a Web Service is akin to a
role specification in which request/response pairs of messages are defined, but
without necessarily constraints on the order in which the requests are received.
3 API description available at url http://docs.amazonwebservices.com/AmazonS3/latest/
API/.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-28-320.jpg)
![3.1. WEB SERVICES 29
3.1.2 Software as a Service
WSDL defines which functionalities a service offers as well as how one com-
municates with the service. However, since their inception, Web services have
gradually turned from remotely accessible libraries to full-fledged applications.
The general idea is to transform existing applications, or create new ones, by
writing independent software components and by establishing communication
sequences between these components. The goal is to:
• ease the deployment of new applications and the development of new com-
ponents;
• ease the changes in an application by containing each one in a single
component;
• rely on the fact that each component is remotely accessible to gain flexi-
bility on the hardware infrastructure, i.e. the actual computers running
the components, for example by relying on a Web server to dispatch a
request to the computer on which the application is deployed.
The separation into atomic components necessitates a way to glue these com-
ponents into applications. This glue is called a business process, and is written
in a language in which, besides the usual assignments, conditionals, and loops
constructs, there exists basic constructs to invoke a remote service. Some of
these languages are scripting languages such as python or Ruby, but we have
chosen to focus on BPEL [128] Business Process Execution Language because
of its natural integration in the WSDL description of a service: services in-
voked are referenced using their WSDL description, and the process itself can
be advertised by publishing a WSDL description of it.
A current trend is also to employ Web Services to outsource the computers in
which a corporation’s applications are executed. I.e. the services are not hosted
on a computer belonging to the corporation but on computers provided by a
third party, who in returns perceives some payment according to the resources
used by the applications. A merit of this cloud computing approach is the
low initial cost of deployment of services as well as the reduced uncertainty
on the running cost/customer ratio, a crucial benefit in nowadays economic
environment.
Model. When analyzing the security of a Web Service, we simply model Busi-
ness Processes with an ordering on the possible input and output messages. But
when considering the access control policy of services we introduce a process de-
scription language which is a simplified version of BPEL, see Chapter 7.
3.1.3 Security Policies
In general terms, a policy controls the possible invocation of the operations of
a service, such as its Quality of Service, or its business logic. In a framework
such as JBOSS, even the business process can be encoded as a policy over the](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-29-320.jpg)
![30 CHAPTER 3. WEB SERVICES
acceptable requests. Instead of analyzing policies in general, we focus on two
types of security-related policies:
• the message-level security policy, which expresses how the data transmit-
ted to and from the service has to be cryptographically secured;
• the access control policy, which is expressed at the level of the application
and expresses when an invocation is legitimate.
Message Protection
There are two main ways to secure the communications of a service with its
partners: a) to impose that the transport protocol must be secured, and b) to
impose the usage of cryptographic primitives to protect the sensitive parts of
the transmitted messages.
Given that there exists secure transport protocols such as TLS, one could
wonder why one would need to further protect the messages. The main moti-
vation for this extra protection is the fact that the protection provided by TLS
is a point-to-point one, whereas complex service interactions depend upon end-
to-end security. A simple example would be the payment of an item purchased
on Internet. One does not necessarily trust the e-commerce web site enough to
send it one’s credit card information, even though they have to be transmitted
to the bank to complete the transaction. Thus the client has to send to the
e-commerce web site her credit card information cryptographically protected in
such a way that: a) this web site will be able to employ the protected data to
complete the transaction with the bank, but also b) this web site will not be
able to derive the credit information from the data. Other applications include
digital contract signing, electronics bidding, etc.
Model. Cryptographically protected messages are simply cryptographic pro-
tocol messages. When analyzing access control policies, which rely on the pay-
load of messages rather than on the cryptography employed to secure the mes-
sages, we partially abstract the message layer by simply assuming that the
payload is either signed, encrypted, or both, or none, by a user and that the
transport protocol is either secured or not. See Chapter 7.
Authentication–Assertion–Authorization
Access control consists in determining whether a given entity has the right,
under the actual known circumstances, to perform a given action on a protected
object. Access control rules emit opinions on whether the access should be
granted or denied, and an access control policy gathers these opinions and uses
a policy combination algorithm to grant or deny the access to the resource. A
rule is said to be applicable on a request if it emits a grant or deny opinion.
In the most simple form rules are totally ordered, and the opinion of the first
applicable rule is the resulting opinion of the set of rules, but other combinations
algorithms can be found e.g. in [173].](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-30-320.jpg)
![3.1. WEB SERVICES 31
Expressibility. Just as Object Oriented programming simplifies the manage-
ment of objects by organizing them in a hierarchy, a lot of research on access
control is focused on the simplest ways to write rules that are both sound w.r.t.
desired policies and easily writable and understandable. In this line we note
the RBAC (Role Based Access Control ) framework proposed by Ferraiolo and
Kuhn [113] that organizes individuals according to the administrative role they
have (doctor, visitor, etc.) together with a role hierarchy that defines the inher-
itance of permissions of junior role r to a senior role r . Access control decisions
are based uniquely on the role played by the requester, on the action, and on
the object in the request. OrBAC [129] refines this model by introducing a hi-
erarchy of contexts in which a request has to be analyzed as well as a hierarchy
on objects. These models often yield very simple policies but at the expense of
expressibility. For example in pure RBAC it is not possible to express that the
same individual, regardless of her role, shall not perform two different actions in
the same execution context (this is called dynamic separation of duty). On the
other side of the spectrum, ABAC (Attribute-Based Access Control ) provides
no hierarchy, and the decision is based solely on the values of a set of attributes
extracted from the request and from the environment. This implies that every
aspect that can influence an access control decision has to be modeled by a
valued attribute, and thus that this type of access control system, while being
able to express any kind of policy, is hard to deploy and manage. Its versa-
tility nonetheless made it the system of choice for Web Service access control
systems such as XACML [173], especially in the currently developed XACML
3.0 version, with its WS profile [9].
Layered model of Access Control. A layered model has emerged over the
years from the industry best practices as well as from the availability of dedicated
systems. Access control in distributed systems is now viewed as consisting in
three interacting components:
Authentication: the first phase is implemented in applications such as Shib-
boleth and consists in the authentication of users. I.e., a user has to
authenticate to one such server using e.g. his login and password or a
more complex authentication protocol, and once the authentication con-
straints imposed on the server are satisfied (e.g. the user has provided a
valid certificate authenticating his signature verification key and has re-
sponded successfully to a challenge-response protocol) the server issues
a token that can be employed by the user to prove his identity to other
services. Alternatively, in the case of SAML Single Sign-On, the server
will authenticate the user to other services.
Assertions: once the user is identified he can negotiate with security services to
obtain assertions that qualify him. For example a user can use his identity
to activate a role and thereby obtain a role membership credential. This
credential can then be employed to gain new ones expressing permissions
associated with this role.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-31-320.jpg)
![32 CHAPTER 3. WEB SERVICES
Authorization: Finally, when trying to execute an action on a resource, the
user decorates his request with the necessary credentials, and an autho-
rization decision is taken based on the value and origin of the provided
attributes.
Model. Given that we are less interested in a user-friendly access control
system than in the analysis of the access control policy of a set of Web Services
we have adopted a formal model of attribute-based access control. We have
abstracted away the authentication phase by using secure channels providing
authentication, and are left with the modeling of the assertion collection part
and of the authorization part of access control. We present in Chapter 7 a
comprehensive model of a distributed access control system for Web Services
where the rules are furthermore modeled as Horn clauses.
3.2 Results achieved in the domain of Web Ser-
vices
I have collaborated with Marwa El Houri, a PhD student I supervised, and
Philippe Balbiani on the definition of a formal model for the analysis of Web
Services [110]. Our final proposal consists in modeling each component in a
Web Service infrastructure by a communicating entity, i.e. an agent that has:
• a store that permits to model a memory, a database, the history of the
service, etc.;
• a trust negotiation policy that indicates which credentials the entity is
ready to share with which other entities on which kind of channel;
• A workflow which consists in a set of tasks. Tasks are recursively defined,
and an authorization rule controls each invocation of a task.
Given the part of an infrastructure (a database system, a human agent, a trust
negotiation engine or a Business Process Engine) modeled by an entity some of
the above parts may be empty.
This model permits us to seamlessly encode Role Based Access Control with
(dynamic) separation or binding of duties constraints as well as advanced fea-
tures such as all surveyed kinds of delegation [110]. We have also enriched it
with cryptographic primitives and secure channels to enable the validation of a
given set of entities w.r.t. untrusted users [110].
In collaboration with Mohammed Anis Mekki—a PhD student I co-supervise
with M. Rusinowitch—and M. Rusinowitch we have considered the choreogra-
phy problem for a set of services. This problem consists in building, given a
finite set of available services, an orchestrator that communicates with these
services to achieve a given goal. I detail this work in Chapter 9. Also presented
in that chapter is the work in collaboration with Tigran Avanesov, M. Rusi-
nowitch and Mathieu Turuani on the choreography problem for services which](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-32-320.jpg)




![Chapter 4
Fundamentals of
First-Order Logic
We introduce in this chapter the formalism and notions that will
be employed in the rest of this document. This chapter is aimed
at presenting first-order logic with an emphasis on resolution,
and should be read as a basis for a course on first-order logic ori-
ented towards resolution and its applications. This focus means
that significant though unrelated notions are lacking. The in-
terested reader can find in particular complements on sequent
calculus and semantic tableaux in [94].
This chapter ends with the definition of equational theories, a
more advanced concept that we need to analyze cryptographic
protocols. In particular we extend the unification notions intro-
duced together with resolution to unification modulo an equa-
tional theory. We also prove a few important facts on equational
unification.
4.1 Facts, sentences, and truth
4.1.1 Reasoning on facts
Consider the following sentences:
• It is summer or the temperature is cold;
• It is not summer or the weather is rainy.
We rely on the excluded-middle law 1 which states that a fact can only be true or
false. As a consequence we can reason on the possible truth value of the fact “It
1 In Scottish courts the result of a criminal prosecution can be either proven (meaning
guilty), not proven, or not guilty. In this case we can have at the same time that the result
of the prosecution is not “proven” and is not “not proven”. Beyond the anecdote logic with
no excluded-middle law (intuitionistic logic, linear logic, . . . ) have been employed fruitfully
37](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-37-320.jpg)
![38 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
is summer”. If it is true then the fact “It is not summer” must be false. Since
the second sentence is true one can deduce that the weather is rainy. But it may
also be the case that the fact “It is summer” is false. Since the first sentence is
true we must then have that the temperature is cold. As a conclusion of these
two sentences, either the temperature is cold or the weather is rainy.
Generally speaking, if A, B1 , . . . , Bn , C1 , . . . , Ck are facts, and the sentences:
• A or B1 or . . . or Bn ;
• not(A) or C1 or . . . or Ck .
are true, then if A is true, not(A) must be false, and thus C1 or . . . or Ck is
true since the second sentence is. Symmetrically if A is false we must have B1
or . . . or Bn because the first sentence is true. This reasoning is sound since if
the assumptions are true then the conclusion must be true.
This reasoning can also be conducted if there is no alternative in one of the
sentences. Assume the following two sentences are true:
• It is day or it is night;
• It is not day.
One ought to conclude that it is night. Another special case is when there is no
alternative in both sentences. For instance assume the following two sentences
are true:
• It is day;
• It is not day.
By following the general scheme given above we deduce that a sentence with
no facts must be true. But the common sense also tells us that the assumption
that both sentences are true does not hold: a fact and its negation cannot be
both true. We reconcile these two conclusions by imposing that a sentence
with no facts must always be false, and rely on the soundness of our deduction
mechanism to deduce (by contrapositive reasoning) that if the conclusion is
false then one of the premises must be false. In this case, i.e. when in a set of
sentences at least one must be false whatever truth value is chosen on the facts,
we say that this set is inconsistent.
The case-based reasoning on sentences illustrated above is called resolution.
It was introduced by Robinson [3] as a reasoning mechanism for the whole of
first-order logic, in which one can e.g. axiomatize Zermelo-Fraenkel set theory.
Outline of this chapter. We begin this chapter with a section on orders,
and review some definitions and properties. Then we define in Section 4.3 the
language employed to describe sentences. We give a semantics to first-order
to reason about the existence of a proof of a theorem, a proof of the negation of a theorem,
and the absence of proof for both a theorem and its negation.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-38-320.jpg)





![44 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
• a (β, α)-atom is a (β, α)-formula;
• if f1 , f2 are (β, α)-formulas then f1 ∨ f2 and f1 ∧ f2 are (β, α)-formulas;
• if f is a (β, α)-formula then ¬f is a (β, α)-formula.
Example 5. Continuing the examples 3 and 4 a formula is an expression like:
¬(inf(abs(minus(x, x )), λ)) ∨ inf(abs(minus(f (x), f (x ))), ε)
Given a formula ϕ where the atoms a1 , . . . , an occur we denote Var(ϕ) (resp.
Const(ϕ)) the set ∪n Var(ai ) (resp. ∪n Const(ai )).
i=1 i=1
4.3.5 Quantifiers
The definition of (β, α)-formulas is still ambiguous. When one writes a(x) ∨ b(x)
it is not clear one means that for some value c of x it is true that a(c) ∨ b(c),
or one means that whatever the value c of x is it is true that a(c) ∨ b(c). In
order to precise the meaning of the variables in the formulas one introduces
existential (for some value of) and universal (for all values of) quantifiers denoted
respectively ∃ and ∀. Formally,
• A (β, α)-formula is a (β, α)-quantified formula with an empty set of quan-
tified variable;
• If ϕ is a (β, α)-quantified formula with a set of quantified variables Q
and x ∈ Var(ϕ) Q then ∃xϕ is a (β, α)-quantified formula with a set of
quantified variables Q ∪ {x};
• If ϕ is a (β, α)-quantified formula with a set of quantified variables Q
and x ∈ Var(ϕ) Q then ∀xϕ is a (β, α)-quantified formula with a set of
quantified variables Q ∪ {x}.
A (β, α)-quantified formula in which every variable is quantified is called a
(β, α)-sentence. Note that in the traditional presentation of sentences in first-
order logic the quantifiers may be interleaved with the logical connectives. The
price of the added complexity (in terms of defining the semantics, the quantified
variables, the handling of variable names clash, etc.) is however paid for nothing:
any (β, α)-sentence in the standard setting is logically equivalent to a formula in
the simpler language described above. An equivalent formula can be effectively
computed by algorithms that rewrite sentences in prenex normal form (see [146,
151, 94], for example).
Example 6. We complete the formula in the preceding example by quantifying
the variables occurring in two different ways, thereby obtaining two different
sentences:
∀x∀ε∃λ∀x , ¬(inf(abs(minus(x, x )), λ)) ∨ inf(abs(minus(f (x), f (x ))), ε)
∀ε∃λ∀x∀x , ¬(inf(abs(minus(x, x )), λ)) ∨ inf(abs(minus(f (x), f (x ))), ε)](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-44-320.jpg)
![4.4. SEMANTICS OF FIRST-ORDER LOGIC 45
The educated reader should by now have noticed that we have given the usual
definitions of continuity and uniform continuity in a normed space. We leave as
an exercise the determination of an arrangement of quantifiers expressing that
the function f is a) bounded, or b) constant.
4.4 Semantics of First-Order Logic
4.4.1 Interpretation
Giving a semantics to a logic means defining when a formula is true. Since the
meaning of quantifiers and logical connectives is fixed, it suffices to define when
an atom is true. This is achieved by interpreting the symbols occurring in a
formula.
Definition 3. (Interpretation) Let α (resp. β) be a functional (resp. relational)
signature, and X be a set of variables. A (α, β)-interpretation I is defined by2 :
• A non-empty set DI , called the domain of the interpretation;
β(p)
• For each predicate symbol p in the domain of β a function I(p) : DI →
{ , ⊥};
α(f )
• For each function symbol f in the domain of α a function I(f ) : DI →
DI .
Given an interpretation I of domain DI a valuation v is a mapping from the
set of variables to elements in DI . Valuations are extended homomorphically
on terms, atoms, and formulas as expected.
The truth value of a sentence ϕ in an interpretation I of domain DI is
denoted [[ϕ]]I is determined as follows:
• If ϕ = ∃xψ(x) then [[ϕ]]I = if, and only if, there exists a valuation v of
domain x such that [[v(ψ(x))]]I = ;
• If ϕ = ∀xψ(x) then [[ϕ]]I = if, and only if, for all c ∈ DI we have
[[vc (ψ(x))]]I = with vc is the valuation mapping x to c;
• If ϕ = ϕ1 ∧ ϕ2 then [[ϕ]]I is if, and only if, [[ϕ1 ]]I = and [[ϕ2 ]]I = ;
• If ϕ = ϕ1 ∨ ϕ2 then [[ϕ]]I = if, and only if, [[ϕ1 ]]I = or [[ϕ2 ]]I = ;
• If ϕ = ¬ϕ1 then [[ϕ]]I = if, and only if, [[ϕ1 ]]I = ⊥;
• If ϕ = p(t1 , . . . , tn ) then [[ϕ]]I = I(p)(I(t1 ), . . . , I(tn ));
2 We note that the interpretation of a variable is not defined. While usually interpretations
are extended over variables with valuations—functions mapping variables in the formula to
elements in the domain of the interpretation—we have chosen to instantiate in the formulas the
variables by the elements of the domain. Given that this interleaving is not defined formally,
this instantiation should be thought of as syntactic sugar.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-45-320.jpg)
![46 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
• Given a valuation v we have [[x]]I = v(x) if x is a variable. Otherwise we
must have t = f (t1 , . . . , tn ), and we define [[t]]I = I(f )([[t1 ]]I , . . . , [[tn ]]I ).
Note that since all the variables in a sentence are bound by a quantifier and
all quantifiers appear first every variable in the formula is in the domain of a
valuation when evaluating an atom. An interpretation that makes a sentence
true is called a model of this sentence.
Definition 4. (Model) Let ϕ be a first-order sentence and I be an interpretation
with [[ϕ]]I = . We say that I is a model of ϕ, and denote I |= ϕ.
Given two formulas ϕ and ψ we also denote ϕ |= ψ the fact that for every
model I of ϕ we have I |= ψ.
Example 7. For instance, consider the following exercise:
Prove that the function f : I → I defined by f : x →
R R
x2 is continuous.
As it was already noted the first formula of Example 6 is the definition of
continuity if one considers the interpretation I:
• with a domain I
R;
• I(inf) =<, the usual order on I
R;
• I(abs) = x → |x|, the function that associates to an element of I its
R
absolute value;
• I(minus) = (x, y) → x − y, the usual subtraction in I
R.
This interpretation is not complete as it lacks the interpretation of the function
symbol f . This last part is contained in the statement of the exercise, with
I(f ) = x → x2 .
4.4.2 Satisfiability, validity
It is clear that the truth of a formula depends on the chosen interpretation. For
instance the first (resp. second) formula of Example 6 is true in the interpre-
tation I of Example 7 if, and only if, f is interpreted by a continuous (resp.
uniformly continuous) function. The goal of automated reasoning techniques
for first-order logic is to decide, given a sentence ϕ, whether:
• there exists at least one interpretation in which ϕ is true;
• or if for all interpretations ϕ is true.
In the former case we say the sentence is satisfiable, and in the latter case that
it is valid.
Definition 5. (Satisfiability, validity) A sentence ϕ is](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-46-320.jpg)
![4.5. FOUNDATIONS OF RESOLUTION 47
• satisfiable if there exists one interpretation in which ϕ is true;
• valid if it is true in any interpretation.
Example 8. The definition of continuity is certainly satisfiable since it is true
in every interpretation I in which I(f ) is a continuous function, but is not valid
since it will be false if one interprets f with a non-continuous function.
For the sake of completeness we also say that a sentence is unsatisfiable if
it is not satisfiable—i.e. is false in every interpretation—, and falsifiable if it is
not valid—i.e. is false in some interpretation.
Logical equivalence. Let us now define the notion of logical equivalence that
we have employed in Section 4.3.5 when stating that every first-order sentence
in which the quantifiers are scattered in the formula, such as ∀x((∃yp(x, y)) ∨
(∀zp(y, z))) is logically equivalent to a sentence in which all the quantifiers ap-
pear in sequence at the beginning of the formula, e.g. ∀x∃y∀z(p(x, y) ∨ p(y, z)).
Definition 6. (Logical equivalence) Two first-order logic sentences ϕ and ψ
are logically equivalent if, and only if, for every interpretation I we have:
[[ϕ]]I = [[ψ]]I
4.5 Foundations of Resolution
The logical equivalence between two first-order sentences means that they have
exactly the same set of models. However as long as one is concerned with sat-
isfiability or validity (by considering the negation of the formula), the relevant
notion is the one of having or not a model. A second equivalence between
first-order sentences, called equisatisfiability, reflects this importance. Two for-
mulas ϕ and ψ are equisatisfiable when ϕ is satisfiable if, and only if, ψ is
satisfiable. This equivalence relation is very coarse since it defines only two
equivalence classes. It is however very useful when considering algorithms that
have to decide whether a given formula is satisfiable. Indeed, this notion al-
lows such algorithms to transform sentences into non-logically equivalent one as
long as the transformations performed change a sentence into an equisatisfiable
one. In particular skolemization first brick of automated reasoning techniques
in first-order logic—transforms any first-order sentence into an equisatisfiable
first-order sentence with no existential quantification. We then prove that when
considering their satisfiability it suffices to interpret these sets of universally
quantified clauses in Herbrand’s interpretations, i.e. interpretations that equal-
ize the functions in the domain with the function symbols in the formula. Then
we prove that to prove the unsatisfiability of a finite set of clauses it suffices to
prove the unsatisfiability of a finite set of instances of these clauses.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-47-320.jpg)

![4.5. FOUNDATIONS OF RESOLUTION 49
domain D as I, equal to I on the symbols in the domains of the signatures α
and β, and such that I (f ) = f I . By construction I is a model of ϕ .
⇐ Let I be a model of ϕ , and let f I = I (f ). By definition every
occurrence of f in ϕ is in the term f (x1 , . . . , xn ). Thus there exists in D an
element b = f (a1 , . . . , an ) such that in ϕ(a1 , . . . , an , b) evaluates to in I .
Thus I’ is an interpretation that satisfies ϕ.
The skolemization lemma can be iterated on a sentence to remove every
existential quantifier from the left to the right. Since each iteration transforms
a sentence into an equisatisfiable one we obtain the following theorem.
Theorem 4.1. (Skolem, [198]) Every first-order sentence ϕ is equivalent with
respect to satisfiability to a universally quantified sentence.
Since the variables in a universally quantified sentence are all bound by
the same quantifier we will often, in the rest of this document and when this
introduces no ambiguity, write sentences without the quantifiers.
4.5.2 Clauses
The logical connectives we have employed to relate the atoms one with another
in a formula share some properties known as de Morgan laws. Among these we
note especially the following ones:
Laws that move the negation down:
¬ ∧ ¬ ∨
∨ ≡ ¬ ¬ ∧ ≡ ¬ ¬
a b a b a b a b
Laws that move the disjunction down:
∨ ∧ ∨ ∧
a ∧ ≡ ∨ ∨ ∧ a ≡ ∨ ∨
b c a b a c b c b a c a
It is clear that using these laws and the fact that ¬¬x ≡ x it is possible to:
• First push the negation downward so that a formula is written as disjunc-
tions and conjunctions of atoms or negation of atoms. We call literals the
formulas that are either atoms or the negation of an atom;
• Then push the disjunction downward, resulting in a formula which is a
conjunction of disjunctions of literals.
In order to complete our transformation of sentences we need another lemma
that permits us to push quantifications downwards.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-49-320.jpg)
![50 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
Lemma 4.3. The formulas ∀x(ϕ(x) ∧ ψ(x)) and (∀xϕ(x)) ∧ (∀xψ(x)) are logi-
cally equivalent.
Proof. We prove only that every model of ∀x(ϕ(x)∧ψ(x)) is a model of (∀xϕ(x))∧
(∀xψ(x)), the converse being similar.
Let I be a model of ∀x(ϕ(x) ∧ ψ(x)) with a domain D = ∅. By definition for
all a ∈ D we have [[ϕ(a) ∧ ψ(a)]]I = , and thus by definition of the evaluation
of ∧, for all a ∈ D we have [[ϕ(a)]]I = and [[ψ(a)]]I = . Thus,
• For every a ∈ D we have [[ψ(a)]]I = , and thus I |= ∀xψ(x);
• For every a ∈ D we have [[ϕ(a)]]I = , and thus I |= ∀xϕ(x);
Thus by definition of the evaluation of the ∧ connective we have I |= (∀xψ(x))∧
(∀xϕ(x)).
We are now ready to sum up the transformations applied. First, we define
a clause as a universally quantified disjunction of literals, i.e. a formula of the
type:
∀x1 , . . . , ∀xn , l1 ∨ . . . ∨ lk
were each literal li is either an atom p(t1 , . . . , tm ) or its negation ¬p(t1 , . . . , tm ).
Defining a first-order theory as a conjunction of clauses, the transformations
described in this section imply the following theorem. Given that a theory is
always a conjunction of clauses it is also viewed as a finite set of clauses.
Theorem 4.2. Every first-order sentence can be effectively transformed into an
equisatisfiable first-order theory.
4.5.3 Herbrand’s theorem
We have seen that there are two distinct levels to first-order logic: a) the lan-
guage level in which formulas are defined; and b) the interpretation level in
which the symbols of a formula are interpreted as functions on a non-empty
domain. In order to avoid heavy notations we have already mixed both levels
when proving the correctness of skolemization, noting that it is possible to avoid
this interleaving of notations by completing the interpretation with an explicit
function that maps every variable to an element of the domain. The question
then arises as to whether one could go further and equate the symbols of the
language with those of the interpretation, or if a strict separation should be
kept.
To answer this question we first introduce a special domain, called the Her-
brand’s domain of a theory T , constructed as follows.
The functional signature of a first-order theory T is denoted αT and is a
function mapping every function symbol appearing in T to its arity. Addition-
ally, if no constant (i.e. symbols of arity 0) occurs in a formula of T we extend
αT on a symbol a not occurring in T with α(a) = 0.
This construction permits one to define the Herbrand’s domain HT of a
theory T as the set of terms T (α). In particular we note that this domain is](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-50-320.jpg)
![4.5. FOUNDATIONS OF RESOLUTION 51
never empty, and is finite if, and only if, every function symbol occurring in T
is of arity 0.
Example 10. Assume:
T = ∀x∀ε∀x ¬(|x − x | < g(x, ε)) ∨ |f (x) − f (x )| < ε
Since T does not contain any constant its functional signature is the function
α:
α = {a → 0, | | → 1, f → 1, − → 2, g → 2}
The Herbrand’s domain HT is the set of terms:
a, |a|, f (a), a − a, g(a, a), ||a||, f (|a|), . . .
One easily sees that the Herbrand’s domain of a first-order theory is denumer-
able, the proof being left as an exercise to the reader.
Given a relational signature βT describing the arity of the predicate symbols
occurring in the clauses of T and the Herbrand’s domain HT we define the
Herbrand’s universe to be the set of atoms p(t1 , . . . , tn ) where β(p) = n and
t1 , . . . , tn ∈ HT . A term in HT or an atom in UT is said to be ground.
Definition 7. (Herbrand’s interpretation) A Herbrand’s interpretation of a
first-order theory T is an interpretation I in which the domain is the Herbrand’s
domain HT of T and such that, for every function symbol f occurring in T we
n
have I(f ) = (t1 , . . . , tn ) ∈ HT → f (t1 , . . . , tn ) ∈ HT .
Thus in a Herbrand’s interpretation the terms are both syntax and semantics
as they occur in the domain and in the formula. We note that since every
interpretation of T must interpret the function symbols occurring in T , the
Herbrand’s domain can be viewed as the set of all the expressions definable
in all interpretations of T . Accordingly given an interpretation I there exists
an embedding ΘI of the Herbrand’s universe into the set of distinct atoms in
I. Sinnce ΘI is a mapping the preimages of the atoms of the interpretation
are disjoints. Thus the truth value of an atom in the interpretation I can be
mapped to the truth value of the atoms in a Herbrand’s interpretation which are
in its preimage. For these reasons Herbrand’s universes are called the Canonical
models of first-order logic.
Given a clause C = ∀x1 . . . ∀xn l1 ∨ . . . ∨ lk of T a ground instance of C is a
clause l1 σ ∨ . . . ∨ lk σ where σ is a substitution mapping the variables x1 , . . . , xn
to ground terms t1 , . . . , tn of the Herbrand’s domain. We let T HT be the set of
all ground instances of all clauses in T .
Lemma 4.4. (Lemma 1.6.1 in [146]) A theory T is satisfiable if, and only if,
T HT is satisfied by a Herbrand’s interpretation.
Proof. ⇒ First let us prove that if T is satisfiable then T HT is satisfied by
a Herbrand’s interpretation. Let I be a model of T of domain D = ∅. If a](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-51-320.jpg)
![52 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
constant a was added to the function symbols occurring in T , fix some c ∈ D
and set I(a) = c. Since I(f ) is defined for every function symbol occurring in
T , by structural induction on the terms, it is trivial that I can be extended
as a mapping from Θ : HT → D. We build a Herbrand’s model U of T HT as
follows:
for each predicate symbol p of arity n and for every ground terms
t1 , . . . , tn ∈ HT let
U(p(t1 , . . . , tn )) = I(p)(Θ(t1 ), . . . , Θ(tn ))
By contradiction assume that U is not a model of T HT . By definition there
exists a clause C = ∀x1 . . . ∀xn l1 ∨ . . . ∨ lk of T and a ground substitution σ
mapping the variables x1 , . . . , xn to ground terms t1 , . . . , tn of the Herbrand’s
domain such that:
U(l1 σ ∨ . . . ∨ lk σ) = ⊥
Reordering the literals if necessary let us fix the notations with atoms a1 , . . . , ak , bk +1 , . . . , bk
such that:
ai If i ≤ k
li σ =
¬bi If i > k
We have U(a1 ) = . . . = U(ak ) = ⊥ and U(bk +1 ) = . . . = U(bk ) = . By
construction every atom ai , bi has an image by Θ. By definition of U we have:
I(Θ(ai )) = ⊥
I(Θ(bi )) =
and thus I(l1 σ ∨ . . . ∨ lk σ) = ⊥. There is an instance of a clause of T which is
not evaluated to true by I, which contradicts the fact that I is an interpretation
of T . Thus U is a Herbrand’s model of T HT .
⇐ Trivial, since assume the existence of an interpretation in which all
instances of all clauses in T are satisfied.
Lemma 4.4 reduces the general problem of the (un)satisfiability of a first-
order theory to the particular case of the existence of a Herbrand’s model.
The cost to pay for this reduction is that we are now looking for a model of an
infinite set of ground clauses. We now follow Quine [183] to prove that it actually
suffices to consider finite sets of ground instances to derive the (un)satisfiability
of this infinite set of ground clauses. The proof relies depends on the notion of
condemnation.
Definition 8. (Condemnation) Let S be a finite set of ground clauses where
the atoms ξ1 , . . . , ξk occur and I be a truth-value assignment I(ξ1 ), . . . , I(ξl )
with l ≤ k. We say that I condemns S if I cannot be extended to a truth-value
assignment I’ on ξ1 , . . . , ξk satisfying S.
We note that when k = l the truth-value assignment condemns the finite set
of ground clauses if, and only if, it does not satisfy this set. Actually we can
relate condemnation with satisfiability even more tightly.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-52-320.jpg)
![4.5. FOUNDATIONS OF RESOLUTION 53
Lemma 4.5. Let S be a finite set of ground clauses. If S is unsatisfiable then
every truth-value assignment condemns S. Conversely, if there exists a set of
atoms Ξ such that every truth-value assignment on Ξ condemns S then S is
unsatisfiable.
Proof. ⇒ Let S be a finite set of clauses and assume there exists a finite
truth-value assignment I that does not condemn S. Then by definition I can
be extended into a truth assignment that satisfies S.
⇐ Assume that there exists a set of atoms Ξ such that every truth-value
assignment on Ξ condemns S. Then in particular every extension on the atoms
on S of truth-value assignment on Ξ does not satisfy S, and thus no truth-value
assignment on the atoms of S satisfies S. Hence S is unsatisfiable.
Herbrand’s Theorem, at least the version we give here and whose proof
follows [183] relates the unsatisfiability of a theory to the unsatisfiability of
finite sets of ground instances of its clauses in the Herbrand’s domain.
Theorem 4.3. (Herbrand) A first-order theory T is unsatisfiable if, and only if,
there exists a finite subset of T HT not satisfied by any Herbrand’s interpretation.
Proof. ⇐ If there is a finite unsatisfiable subset of T HT then by definition
T HT is unsatisfiable, and thus by the contrapositive of the direct direction of
Lemma 4.4 the theory T is unsatisfiable.
⇒ By the contrapositive of the converse direction of Lemma 4.4 we have
T unsatisfiable implies T HT unsatisfiable by a Herbrand’s interpretation. Let
ξ1 , ξ2 , . . . be an enumeration of the ground atoms in the Herbrand’s universe of
T , and let us consider the interpretation I that maps the sequence of atoms
ξ1 , ξ2 , . . . to the truth value t1 , t2 , . . . such that:
ti = iff the truth value assignment t1 , . . . , ti−1 , does not
condemn any finite subset of clause instances.
Since T HT is unsatisfiable there exists at least one instance C of a clause of
T which is not satisfied by the truth-value assignment we have just defined. Let
ξj be the atom in C that is enumerated last. By maximality the truth value of all
atoms occurring in C is determined by t1 , . . . , tj . Since C is not satisfied by the
truth assignment t1 , . . . it is not satisfied by the truth assignment t1 , . . . , tj . A
fortiori we note that t1 , . . . , tj condemns a finite subset {C} of clause instances.
This yields the existence of a finite j such that t1 , . . . , tj condemns a finite subset
of clause instances.
Let h be a minimal integer such that t1 , . . . , th condemns a finite subset of
clause instances. For that h we must have th = ⊥ by the choice of the sequence
of truth values. So:
(i) t1 , . . . , th−1 , ⊥ condemns a finite subset ω of clause instances;
(ii) Since we have not chosen th = by definition of the sequence we also have
that t1 , . . . , th−1 , condemns a finite subset ω of clause instances.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-53-320.jpg)
![54 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
This implies that if h > 1 the truth-value assignment t1 , . . . , th−1 condemns
the finite subset of clause instances ω ∪ ω , which contradicts the minimality of
h. Thus we must have h = 1. But then the points (i) and (ii) above imply
that regardless of whether one chooses t1 = or t1 = ⊥ the finite set of clause
instances ω ∪ ω is condemned by t1 . Since there is no truth-value assignment
that satisfies ω ∪ ω this is a finite unsatisfiable subset of T HT .
The direct part of the proof actually proves an important property of first-
order logic known as compacity, in which the interpretation is not restricted to
be a Herbrand’s interpretation.
Theorem 4.4. (Compactness theorem) A set of clauses is unsatisfiable if, and
only if, there exists a finite and unsatisfiable set of clause instances.
4.5.4 Concluding remarks
The theorem we have attributed to Herbrand is quite different from the original
statement by Herbrand who considered the provability of a first-order theory.
The standard proof for our statement of Herbrand’s theorem is based on the
finiteness of proofs, and thus relies on the notion of provability. Formally, if S
is a set of formulas, S A denotes the existence of a proof (which is a finite list
of formulas) of the formula A from S in a predicate calculus whose language
includes the symbols of S ∪ A. A set S of formulas is inconsistent if there exists
a formula A such that S A ∧ ¬A. If S is not inconsistent it is consistent. The
consistency—a syntactic notion given that one is interested in the manipulation
of formulas—is related to satisfiability by the following theorem.
Theorem 4.5. (G¨del Completeness Theorem) A first-order theory T is con-
o
sistent if, and only if, it is satisfiable.
This theorem implies the existence of a finite proof of A ∧ ¬A for an unsat-
isfiable theory T . The formulas in this proof provide an example of a finite set
of unsatisfiable instances of the clauses in T when T is unsatisfiable, and thus
the compactness theorem 4.4. This theorem is then employed to directly obtain
a finite unsatisfiable subset of clause instances from T HT .
Instead of this usual proof we have prefered to present the approach of
Quine [183] which is purely model-theoretic and based on an enumeration of the
set of atoms in a Herbrand’s interpretation. In particular we believe that his
proof of the compactness Lemma is an excellent introduction to resolution as well
as to the ordering refinements of resolution. We note that this model-theoretic
approach was also followed in the second chapter of [146] in a presentation
based on semantic trees. That presentation opened the way to the semantic trees
approach that eventually lead to completeness results of ordered paramodulation
and superposition [189]. We refrain from going further down that road to focus
on our own results even though some are based on these ordering refinements.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-54-320.jpg)
![4.6. RESOLUTION 55
4.6 Resolution
While knowing that a first-order sentence is valid certainly seems important, it
is much more obscure as to why would anyone be interested in sentences that
are always false. The main rational of this interest is that the negation of an
always-true sentence is an always-false sentence. Thus to prove that a sentence
is valid it suffices to prove that its negation is unsatisfiable.
The resolution method was defined by Robinson [3] to turn the mathemat-
ical proof of the existence of a finite unsatisfiable set of ground clauses into a
procedure that searches for a finite witness sets. In this section we first present a
generic procedure that recognizes unsatisfiable theories in Subsection 4.6.1, and
discuss its shortcomings. Then we present ground resolution in Subsection 4.6.2
as a procedure that turns Quine’s proof of Herbrand’s Theorem into an effec-
tive method. The abstraction from ground instances relies on unification, and
more precisely on the existence of most general unifiers, which are defined in
Subsection 4.6.3. These most general unifiers are employed in Subsection 4.6.4
to simulate ground resolution on finite sets of ground instances by resolution.
4.6.1 Recognizing unsatisfiable theories
Assume that a first-order theory T is unsatisfiable. Then by Theorem 4.4 there
exists a finite unsatisfiable set of ground instances of clauses in T which is
unsatisfiable. This provides a procedure that recognizes the unsatisfiable first-
order theories, described in Algorithm 4.1. This algorithm is effective in the
Algorithm 4.1: Naive algorithm recognizing whether T is unsatisfiable
for all finite sets of ground instances S of clauses in T do
if S is unsatisfiable then
return theory unsatisfiable
end if
end for
sense that:
• it is possible to enumerate all the terms in the Herbrand’s domain of the
theory T , for example by first enumerating all the terms with one symbol,
then all the terms with 2 symbols, and so on, given that each of these sets
is finite;
• it is thus possible to enumerate all the ground atoms by enumerating
first the ground atoms in which the predicate symbol takes as arguments
the first term, then the two first terms, and so on. Since the number of
predicate symbols is finite each of these sets is finite;
• it is thus possible to enumerate all the ground instances of clauses in T by
considering first all the ground instances that contain only the first atom,](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-55-320.jpg)
![56 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
then all the ground instances that contain the first and the second atom,
and so on. Since each clause contains a finite number of atoms, and since
the number of clauses is finite, each set in this enumeration is finite.
• it is thus possible to enumerate all the finite sets of ground instances of
clauses in T by first enumerating the singleton set containing the first
clause, then the sets contained in the set of the two first clauses, and so
on. Since the number of subsets of a finite set is finite, each of these sets
is finite.
Then checking whether a finite set of ground clauses is unsatisfiable can be done
by looking at all the possible interpretations e.g. by writing a truth table.
Given that this algorithm blindly enumerates all the possible instances of a
first-order theory T , it is clear that it is not adequate for recognizing unsatis-
fiable theories in practice. The resolution principle was introduced by Robin-
son [3] to guess efficiently subsets of clause instances that might be unsatisfiable.
Before presenting resolution in Subsection 4.6.4 we present in Subsection 4.6.2
an alternative approach to truth-tables to check for the unsatisfiability of a finite
set of ground clauses, called ground resolution.
4.6.2 Ground resolution
Let S = {C1 , . . . , Cn } be a finite set of ground clauses. Since S is finite the
set of atoms occurring in S is finite. Informally, the ground resolution principle
consists in reducing the set S to an equisatisfiable finite set of clauses S where
the number of distinct atoms occurring in S is strictly less than the number of
distinct atoms occurring in S. This overall reduction is called the resolution on
ξk of S, and consists in the eager application in order of each of the following
rules (written modulo a permutation of literals):
Ground elimination on ξk : Remove from S all the ground clauses ξk ∨ ¬ξk ∨
C;
Ground factorization of ξk : From a ground clause l ∨l ∨C deduce the clause
l ∨ C where l is the literal ξk or ¬ξk ;
Ground resolution on ξk : From the two ground clauses ξk ∨ C1 and ¬ξk ∨ C2
form the clause C1 ∨ C2 .
Since a clause eliminated by ground elimination on ξk is satisfied whatever the
truth assignment to ξk is, it is clear that a set of clauses S is unsatisfiable if,
and only, S {C = ξk ∨ ¬ξk ∨ C | C ∈ S} is satisfiable.
Lemma 4.6. A truth-value assignment satisfies l ∨ l ∨ C if, and only if, it
satisfies l ∨ C.
Proof. Let I be a truth-value assignment. By definition of the interpretation
of disjunctions, If [[l]]I = then [[l ∨ l ∨ C]]I = [[l ∨ C]]I = . If [[l]]I = ⊥ then
[[l ∨ l ∨ C]]I = [[l ∨ C]]I = [[C]]I .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-56-320.jpg)
![4.6. RESOLUTION 57
Lemma 4.7. For any atom ξ not occurring in C1 nor in C2 , a truth-value
assignment that does not satisfy C1 ∨ C2 condemns {ξ ∨ C1 , ¬ξ ∨ C2 }.
Proof. By contrapositive reasoning. Let I be a truth-value assignment with
[[C1 ∨ξ]]I = [[C2 ∨¬ξ]]I = . Then if [[ξ]]I = we have [[C2 ∨¬ξ]]I = [[C2 ]]I = ,
and thus [[C1 ∨ C2 ]]I = by definition of the interpretation of the disjunction.
Same reasoning if [[ξ]]I = ⊥.
Also, if S is a set of ground clauses on which the ground elimination on ξk
has been performed, then every clause C ∈ S contains only the literal ξk , or
its negation ¬ξk , or none of them. Then, applying ground factorization on ξk
on this set yields a set of clauses in which every clause contains at most one
occurrence of a literal ξk or ¬ξk . Thus and wlog we can assume the set S can
be written as the disjoint union of three sets of clauses S+ , S− , S0 such that:
S+ = {ξk ∨ C | ξk ∨ C ∈ S and the atom ξk does not occurs in C }
S− = {¬ξk ∨ C | ¬ξk ∨ C ∈ S and the atom ξk does not occurs in C }
S0 = S (S+ ∪ S− )
The eager application of the ground resolution on ξk on clauses of S is called
the resolution on ξk of S, is denoted Resgr (ξk , S), and is the set of clauses:
Resgr (ξk , S) = S0 ∪ {C ∨ C | ξk ∨ C ∈ S+ and ¬ξk ∨ C ∈ S− }
With respect to satisfiability, this principle is sound, that is if Resgr (ξk , S) is
unsatisfiable then S is unsatisfiable, and complete, that is if S is unsatisfiable
then Resgr (ξk , S) is unsatisfiable. Let us prove these simple facts.
Lemma 4.8. (Soundness) Assume S is a set of clauses on which ground elim-
ination and factorization on ξk have been eagerly applied. If Resgr (ξk , S) is
unsatisfiable then S is unsatisfiable.
Proof. Assume Resgr (ξk , S) is unsatisfiable, i.e. for each truth-value assignment
I = t1 , . . . , tk−1 to the atoms ξ1 , . . . , ξk−1 there exists a clause CI ∈ Resgr (ξk , S)
which is not satisfied by I. Writing CI as the disjunction of literals l1 ∨ . . . ∨ lm
this means that I interprets each of these li as false. If CI ∈ S0 then we have
found a clause in S which is condemned by I. Otherwise by definition we have
CI = C ∨ C with C1 = ξk ∨ C and C2 = ¬ξk ∨ C in S. It is then clear
that the subset {C1 , C2 } of S is condemned by I. Thus every interpretation
I = t1 , . . . , tk−1 condemns a non-empty set of clauses in S, and thus S is
unsatisfiable by Lemma 4.5.
Lemma 4.9. (Completeness) If S is unsatisfiable then Resgr (ξk , S) is unsatis-
fiable.
Proof. Since S is unsatisfiable every truth-value assignment I = t1 , . . . , tk−1 to
the atoms ξ1 , . . . , ξk−1 condemns S by Lemma 4.5. Thus for every interpretation
I on ξ1 , . . . , ξk−1 the set of subsets of S condemned by I is not empty. Let us
choose a minimal one (for inclusion) UI .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-57-320.jpg)
![58 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
Claim 1. For every I either UI = {C} with C ∈ S0 or UI ⊆ S+ ∪ S− .
Proof of the claim. If UI ∩ S0 = ∅ then this intersection contains a
clause C. Since the atom ξk does not occur in C, this clause is either
satisfied or not satisfied by I. In the first case UI is not minimal since
every extension of I satisfies C. In the second case C is also condemned
by I, and thus the minimality of UI for inclusion implies UI = {C}. ♦
Claim 2. If UI ⊆ S+ ∪ S− then UI ∩ S+ = ∅ and UI ∩ S− = ∅.
Proof of the claim. Assume UI ⊆ S+ ∪ S− and wlog UI ∩ S+ = ∅. If
UI ∩ S− = ∅ then I = t1 , . . . , tk−1 , satisfies UI , thereby contradicting
that UI is condemned by I. ♦
Claim 3. Assume ξk ∨ C ∈ UI ∩ S+ and ¬ξk ∨ C ∈ UI ∩ S− . Then C ∨ C is
not satisfied by I.
Proof of the claim. If I satisfies C (resp. C ) then every extension of
I satisfies ξk ∨ C (resp. ¬ξk ∨ C ). This would contradict the minimality
of UI . Thus I satisfies neither C nor C , and thus I does not satisfy
C ∨C . ♦
It is now clear that S unsatisfiable implies Resgr (ξk , S) unsatisfiable. Indeed
for every interpretation I = t1 , . . . , tk−1 , in the first case of Claim 1 I does not
satisfy a clause in S0 ⊆ Resgr (ξk , S) and in the second case it does not satisfy a
clause in Resgr (ξk , S) S0 by Claim 3. Thus Resgr (ξk , S) is unsatisfiable.
We note that since the clauses are normalized the atom ξk does not occur
in Resgr (ξk , S) for any finite set of ground clauses S. Since only finitely many
atoms occur in S it is clear that applying resolution on a set of ground clauses S
terminates with a set of clauses that does not contain any atom, and therefore
any literal. There are two possibilities for this set:
• the obvious one is that the final set is empty. In this case we note that
every clause in this set is satisfiable, and thus this final set is satisfiable;
• another possibility is that this set contains a clause which is an empty
disjunction of literals. Since a clause is interpreted as true if at least one
of its literal is interpreted as true, this clause is unsatisfiable.
The clause which is an empty disjunction of literals is denoted [ ].
Example 11. (Satisfiable set of clauses) Consider the set S = {a, a ∨ b, a ∨ ¬b}.
We have:
Resgr (b, S) = {a, a ∨ a} = {a, a} = {a}
Resgr (a, S) = ∅
Resgr (a, Resgr (b, S)) = ∅
Since the final set is empty we conclude that S is satisfiable.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-58-320.jpg)
![4.6. RESOLUTION 59
Example 12. (Unsatisfiable set of clauses) Consider the set S = {¬a, a ∨ b, a ∨
¬b}.We have:
Resgr (b, S) = {¬a, a ∨ a} = {¬a, a}
Resgr (a, S) = {¬b, b}
Resgr (a, Resgr (b, S)) = {[ ]}
We summarize the results of this section with the following theorem.
Theorem 4.6. Let S be a finite set of ground clauses over the atoms ξ1 , . . . , ξk .
Then S is unsatisfiable if, and only if, Resgr (ξ1 , . . . Resgr (ξk , S)) contains the
empty clause.
4.6.3 Unification and Most General Unifiers
In the rest of this section we will try to apply the ground resolution and fac-
torization rules before knowing the ground instance of the clauses. This implies
we have to be able to describe the set of equal ground instances of two distinct
atoms, and furthermore to describe this set with one atom. The process of
computing this new atom is called unification. Since the proofs and algorithms
in this subsection apply to atoms as well as to terms, we will consider only the
case of the unification of terms.
Example 13. Consider the two terms t1 = f (x, g(y, a)) and t2 = f (z, v).
Though they are different, we have:
• If σ = {x → b, y → b, z → b, v → g(b, a)} then t1 σ = t2 σ;
• If τ = {x → c, y → b, z → c, v → g(b, a)} then t1 τ = t2 τ ;
• Actually for any term t, for the substitution θt = {x → t, y → b, z →
t, v → g(b, a)} then t1 θt = t2 θt ;
• Even more generally, for any terms t, t , the substitution θt,t = {x →
t, y → t , z → t, v → g(t , a)} we have t1 θt,t = t2 θt,t ;
• Instead of quantifying universally on terms, we can use two variables x1
and x2 , form the substitution σx1 ,x2 = {x → x1 , y → x2 , z → x1 , v →
g(x2 , a)}, and remark that:
– t1 σx1 ,x2 = t2 σx1 ,x2 , and thus σx1 ,x2 makes the terms equal;
– For any substitution τt,t = {x1 → t, x2 → t } we have σx1 ,x2 τt,t =
θt,t .
Example 13 leads us to the definition of several notions. First let us name
the substitutions that equalize two terms.
Definition 9. (Unifier) A substitution σ is a unifier of two terms t, t if tσ = t σ.
Given two terms t, t we denote Σ(t, t ) the set of unifiers of t and t .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-59-320.jpg)

![4.6. RESOLUTION 61
σj+1 = σj θj,j+1 maps a variable to a variable, and thus the number of
variables in the σj for j > i0 is decreasing, and thus becomes constant
after an index j0 . Thus for all j > j0 the substitution θj,j+1 is a one-to-
one correspondence between variables, and therefore for j > j0 all the σj
are equivalent modulo ≡mgt .
Given the second point of Lemma 4.10 we usually say “modulo a renaming
of variables” rather than writing explicitly ≡mgt . Since we have a pre-ordering
on substitutions we can consider the minimal elements in this ordering. Getting
back to Example 13, these minimal elements are like σx1 ,x2 since by definition
of the ordering every unifier can be written as the composition of a minimal
unifier and another substitution.
Definition 11. (Most general unifiers) The set of most general unifiers of t and
t is denoted Σmgu (t, t ) and is the set of minimal elements for mgt of Σ(t, t ).
When defining resolution in [3] Robinson proved the following lemma.
Lemma 4.11. (Unicity of most general unifiers) Given two terms t, t either
Σmgu (t, t ) = ∅ or all elements in it are equal modulo a renaming of variables.
The proof of Lemma 4.11 is constructive in the sense that it results from
the direct computation of a unifier whose instances form the set of all unifiers.
Before presenting this algorithm let us prove a sequence of lemmas that justify
its soundness.
Lemma 4.12. (Extension of equality) Assume t, t have a unifier σ. Then for
all p ∈ Pos(t) ∩ Pos(t ) we have (t)|p σ = (t )|p σ
Proof. The equality tσ = t σ means that every position p ∈ Pos(tσ) we have
(tσ)|p = (t σ)|p . If p ∈ Pos(t) (resp p ∈ Pos(t )) we have t|p σ = (tσ)|p (resp.
t|p σ = (t σ)|p . Hence the equality
A consequence is the following lemma that relates the subterms of t and t .
Lemma 4.13. (No clash) Assume t, t have a unifier σ. Then for all p ∈
Pos(t) ∩ Pos(t ) we have either Symb(t, p) = Symb(t , p) or at least one of
{Symb(t, p), Symb(t , p)} is a variable x.
Proof. For p ∈ Pos(t) ∩ Pos(t ) we have t|p σ = t|p σ. Assume Symb(t, p) is not
a variable, and thus is a function symbol f . By definition the equality of terms
implies the equality of their root symbols, and thus f is the root of t|p σ. Two
cases can occur:
• If Symb(t , p) is a function symbol g, then since the root symbol of t|p σ is
f we must have g = f ;
• Otherwise Symb(t , p) is a variable, and thus t|p is a variable.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-61-320.jpg)
![62 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
Lemma 4.14. (Variable replacement) Assume there exists p ∈ Pos(t) ∩ Pos(t )
such that t|p = x ∈ X and t|p = y ∈ X . Let θ = {x → y}. Then every unifier σ
of t and t is a unifier of tθ and t .
Proof. For every unifier σ we must have by Lemma 4.12 t|p σ = t|p σ, and thus
xσ = yσ.
Lemma 4.15. (Term replacement) Let t and t be two unifiable terms, and
assume there exists p ∈ Pos(t) ∩ Pos(t ) such that t|p = x and t|p is a non-
variable term. Then we have:
• x ∈ Var(t|p );
/
• The substitution θ = {x → t|p } is such that .
– Σ(t, t ) ⊆ Σ(tθ, t θ);
– Every unifier σ ∈ Σ(tθ, t θ) with xσ = xθσ is in Σ(t, t )
Proof. • for every unifier σ of t and t we have xσ = t|p σ. However since t|p
is not a variable, if x ∈ Var(t|p ) then xσ is also a strict subterm of t|p σ,
which is a contradiction.
• For any unifier σ of t and t we must have xσ = t|p σ = (xθ)σ. Given the
definition of θ, for every variable y = x we have yθσ = yσ. Thus for every
variable z we have zσ = zθσ, and therefore every unifier of t and t is a
unifier of tθ and t θ. Conversely, if a unifier σ of tθ and t θ is such that
xσ = xθσ it is clear that it is also a unifier of t and t .
We are now ready to present a unification algorithm of two terms t and
t . The procedure we present is recursive, and certainly not fit for the real
computation of most general unifiers, which can be done in linear time [152].
One easily proves that, invoking the procedure with the identity substitution,
that the variables of Algorithm 4.2:
• At each step the domain of θ is disjoint from Var(t) ∪ Var(t );
• The number of variables in Var(t) ∪ Var(t ) strictly decreases at each
iteration, which ensures the termination of the procedure;
• When Unif(t, t , Id) is invoked, at each subsequent call of Unif(t1 , t2 , θ)
we have Σ(t, t ) = {θσ | σ ∈ Σ(t1 , t2 )};
• Consequently, this procedure always halt, and when it returns a substi-
tution θ on the invocation Unif(t, t , Id) we have tθ = t θ and for every
substitution σ ∈ Σ(t, t ) there exists τ such that θτ = σ.
Thus the returned substitution is smaller for mgt than any substitution
in Σ(t, t ). This proves Lemma 4.11. From now on this substitution will be
denoted, when Σ(t, t ) = ∅, mgu(t, t )](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-62-320.jpg)
![4.6. RESOLUTION 63
Properties of unification
We now state the property of unification that is critical for lifting ground reso-
lution to resolution.
Lemma 4.16. Let t and t be two terms such that Var(t) ∩ Var(t ) = ∅ and
such that there exists two substitutions σ and τ with tσ = t τ . Then t and t
have a most general unifier.
Proof. Consider the set S of couples of terms {t, t } with Var(t) ∩ Var(t ) = ∅
such that there exists σ, τ with tσ = t τ but t and t do not have a mgu.
The lemma states that the set S is empty. Let us prove this emptiness by
contradiction. Assume S = ∅ and consider the ordering on couples (t1 , t1 ) <
(t2 , t2 ) iff t1 is a subterm of t2 and t1 is a subterm of t2 . Since the subterm
ordering is well-founded, this ordering on pairs is well-founded. Thus S = ∅
implies that S has a minimal element (t, t ).
First let us note that neither t nor t can be a variable, for if e.g. t is
a variable, then Var(t) ∩ Var(t ) = ∅ implies that t ∈ Var(t ) and thus the
/
unification of t, t terminates immediately and returns the mgu {t → t } by
Lemma 4.15.
Thus we must have t = ft (t1 , . . . , tn ) and t = ft (t1 , . . . , tm ) for some func-
tion symbols ft , ft of respective arities n and m. Then since tσ = t τ we must
have ft = ft and n = m. Thus if t and t do not have a mgu, there exists
1 ≤ i ≤ b such that ti and ti do not have a mgu. But then the couple (ti , ti ) is
in S, and contradicts the minimality of (t, t ). Thus S must be empty.
4.6.4 Resolution
When considering Algorithm 4.1, ground resolution is of little help, given that it
comes into action only once a finite set of ground instances has been chosen. In
his presentation of Resolution in [3] Robinson comments Herbrand’s Theorem by
saying that to be of effective use one would need a “. . . benevolent and omniscient
demon who could provide us, in reasonable time, with a proof set 4 . . . ”. Resolu-
tion is then presented as one such demon who computes the ground instances
of the clauses in the theory T while applying ground resolution. It is based on
ground resolution but relies on most general unifiers to build incrementally the
instances of the clauses. One difficulty of not knowing the ground instance is
that the normalization phase of ground resolution cannot be conducted deter-
ministically: one does not know whether the instances of two literals in a clause
are equal. Given the importance of normalization for the completeness of reso-
lution, we introduce a factorization rule that non-deterministically guesses the
common instances of literals by trying to unify literals and, when succeeding,
adds the “normalized” clause to the set of clauses. Then we present a resolu-
tion rule, also based on unification and also applied non-deterministically, that
guesses when a ground resolution rule can be applied between two instances of
two clauses. Then we prove that applying non-deterministically these two rules
4a set of atoms with which the clauses are instantiated](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-63-320.jpg)
![64 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
permits one to simulate the operations of labeled resolution. This simulation
implies that the empty clause is reachable by resolution and factorization from
a set of clauses S if, and only if, S is unsatisfiable.
Definition 12. (Factor) Let C = L1 ∨ L2 ∨ C be a clause and assume σ =
mgu(L1 , L2 ). Then (L1 ∨ C)σ is a factor of C.
Definition 13. (Resolvent) Let L1 ∨ C, ¬L2 ∨ C be two clauses of disjoint sets
of variables and assume σ = mgu(L1 , L2 ). Then (C ∨ C )σ is a resolvent of C.
The computation of a factor of a given clause is called factorization, and the
computation of the resolvent of two clauses is called resolution. The application
of the Factorization rule on a set of clauses S consists in:
(i) extracting C from S;
(ii) trying to apply the rule (a) of Figure 4.1 on C;
(iii) When succeeding, adding the factor of C to S.
Similarly, the application of the resolution rule on a set of clauses S consists in:
(i) extracting two clauses C1 and C2 from S;
(ii) renaming the variables of C2 so that the domains of C1 and C2 are disjoints;
(iii) trying to apply the rule (b) of Figure 4.1 on C1 and C2 ;
(iv) When succeeding, adding the resolvent of C1 and C2 to S.
We call resolution the iterated application of the factorization and resolution
rules.
L1 ∨ L2 ∨ C L1 ∨ C ¬L2 ∨ C
σ = mgu(L1 , L2 ) σ = mgu(L1 , L2 )
(L2 ∨ C)σ (C ∨ C )σ
(a) Factorization F ac(L1 , L2 , C) (b) Resolution Res(L1 , L2 , L1 ∨ C, ¬L2 ∨ C )
Figure 4.1: The (a) factorization and (b) resolution rules
Definition 14. (Simulation relation) Let S be a set of clauses and Sg be a set
of ground clauses. We say that S simulates Sg , and denote Sg S, if for every
Cg ∈ Sg there exists C ∈ S and a ground substitution σ such that Cσ = Cg
modulo a reordering of literals.
Assume a set of clauses S is unsatisfiable. Then by Herbrand’s Theorem
there exists a finite set Sg of ground instances of clauses in S which is unsat-
isfiable. We trivially have Sg S. Since Sg is a finite and unsatisfiable set of
ground clauses, Theorem 4.6 implies that a finite sequence of normalization and
ground resolution ends with a set of clauses that contains the empty clause [ ].](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-64-320.jpg)
![4.6. RESOLUTION 65
Lemma 4.17. (Lifting lemma) Let l1 ∨ C1 and ¬l2 ∨ C2 be two clauses with
Var(l1 ∨ C1 ) ∩ Var(¬l2 ∨ C2) = ∅, and σ1 , σ2 be two ground substitutions such
that l1 σ1 = l2 σ2 . Then there exists two substitutions θ and τ such that:
• θ is the most general unifier of l1 and l2 ;
• (C1 ∨ C2 )θτ = C1 σ1 ∨ C2 σ2 .
Proof. The hypothesis implies in particular that Var(l1 ) ∩ Var(l2 ) = ∅. Thus
by Lemma 4.16, θ = mgu(l1 , l2 ) is defined and there exists τ0 such that, for x ∈
Var(l1 ) ∪ Var(l2 ) we have xθτ0 = xσ1 = xσ2 . We extend τ0 into a substitution
τ on variables in (Var(C1 ) ∪ Var(C2 )) (Var(l1 ) ∪ Var(l2 )) by setting xτ = xσ1
(resp. xτ = xσ2 ) if x ∈ Var(C1 ) Var(l1 ) (resp. x ∈ Var(C2 ) Var(l2 )).
Lemma 4.18. Let C = l1 ∨l2 ∨C and assume there exists a ground substitution
σ with l1 σ = l2 σ. Then there exists a most general unifier θ of l1 and l2 , and
l1 σ ∨ Cσ is a ground instance of l1 θ ∨ Cθ.
Proof. Since l1 σ = l2 σ the atoms l1 and l2 are unifiable, and thus θ = mgu(l1 , l2 )
is defined. Since θ is a most general unifier of l1 and l2 and σ is a unifier of
l1 and l2 , there exists a substitution τ such that θτ = σ. Hence l1 σ ∨ Cσ is a
ground instance of l1 θ ∨ Cθ.
Lemma 4.17 states that the ground resolvent of the ground instances of two
clauses with disjoint sets of variables is a ground instance of a resolvent of these
two clauses. Similarly Lemma 4.18 states that the ground factor of a ground
instance of a clause C is a ground instance of a factor of the clause C.
As a consequence for each transformation applied on a set of ground clauses
simulated by S (except the elimination of a trivially satisfiable clause or of the
clauses that contain the resolved atom, but this does not compromise the simu-
lation) there exists a corresponding application of the factorization or resolution
rule on S that preserves the simulation relation. There is only a finite number of
ground factorization and resolution applicable on any given finite set of ground
instances of clauses in S. If the finite set of ground instances is unsatisfiable
then the final simulated set of ground clauses contains [ ] by Theorem 4.6. Since
the clause [ ] can only be simulated by itself modulo a reordering of literals we
have the following theorem.
Theorem 4.7. (Completeness of resolution) Let S be a finite and unsatisfiable
set of clauses. Then there exists a finite sequence of applications of the resolution
and factorization rules that reaches a set of clauses S that contains [ ].
We note that if Sg is a finite and unsatisfiable set of ground instances of S
it is possible to apply a resolution or factorization rule on S that has no ground
counterpart. Also some clauses are eliminated when applying ground resolution.
Thus the set of clauses we obtain from S by applying factorization and resolution
rules typically contains clauses that do not simulate any ground clause obtained
from Sg . Next theorem states that while that may be true, the addition to S of
these “non-simulating” clauses never turns S into an unsatisfiable set of clauses
unless S is unsatisfiable before the application of any rule.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-65-320.jpg)
![66 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
Theorem 4.8. (Soundness of resolution) Let S be a finite set of clauses and
C be either a factor of a clause in S or the resolvent of two clauses in S. If
S ∪ {C} is unsatisfiable then S is unsatisfiable.
Proof. Let S = S∪{C} where C is either a factor of a clause in S or the resolvent
of two clauses in S, and by contrapositive reasoning assume that S is satisfiable.
By Theorem 4.3 there exists an Herbrand’s interpretation I that satisfies every
instance of a clause in S. Assume that I does not satisfy every instance of a
clause in S . By construction of S there exists a ground substitution σ such
that I does not satisfy the clause Cσ.
• If C is a factor of a clause Cf ∈ S then Lemma 4.6 implies that Cf σ is
also not satisfied by I, a contradiction with the assumption that I is a
model of S;
• If C is the resolvent of two clauses ξ1 ∨ C1 , ¬ξ2 ∨ C2 ∈ S obtained by
applying the substitution θ, i.e. C = (C1 ∨ C2 )θ then let τ = θσ. We have
that I does not satisfy any literal in (C1 ∨ C2 )τ whereas it satisfies both
(ξ1 ∨ C1 )τ and (ξ2 ∨ C2 )τ . A case-based analysis on whether I satisfies
ξ1 τ or ¬ξ2 τ yields a contradiction.
We thus have the soundness of the factorization and resolution rules. If
starting from a set S a finite sequence of application of these rules reaches a set
S containing [ ] then S is unsatisfiable. And if S is unsatisfiable one such finite
sequence exists.
Theorem 4.9. Let S be a finite set of clauses. Then S is unsatisfiable if,
and only if, there exists a finite sequence of applications of the resolution and
factorization rules that reaches a set of clauses S that contains [ ].
Note that in Theorems 4.7 and 4.8 we mentioned the existence of a finite
sequence of applications of the rule F ac(L1 , L2 , C) and Res(L1 , L2 , C1 , C2 ), but
never stated that we were sure to apply this sequence. However there is always
a finite number of choices for applying resolution or factorization on each set of
clauses obtained from S. It is thus possible to enumerate all the possible rule
applications starting from S. While this enumeration is in general infinite, it will
reach the empty clause if, and only if, the starting set of clauses is unsatisfiable.
4.7 First-order Logic with Equality
In Herbrand’s theorem, the cornerstone of the reduction of any interpretation
satisfying a theory T to a Herbrand’s interpretation satisfying T is that in
the latter domain, the function symbols are interpreted as one-to-one functions
of disjoint image. For this reason Herbrand’s interpretations fail to capture
natively simple facts such as 1 + 1 = 2: the terms on the two sides of the](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-66-320.jpg)
![4.7. FIRST-ORDER LOGIC WITH EQUALITY 67
equality are syntactically distincts, and thus this atom may be interpreted as
true or false.
It is obvious that for expressiveness reasons, it is important to handle effi-
ciently the equality symbols to be able to reason on algebraic structures. We
review in this section additional clauses that can be added to a theory that
ensures that in any interpretation I satisfying T the equality atoms will be in-
terpreted as they should (e.g. that x = y implies y = x and f (x) = f (y)). Then
we present the special case of equational theories, which are sets of universally
quantified unary positive clauses, and are the core of my work on the refutation
of cryptographic protocols.
4.7.1 Axiomatizing Equality in First-Order Logic
The first approach consists in adding to a first-order theory T that contains
the equality predicate clauses that express its properties. Since equality is a
congruence it must satisfy the follow axioms w.r.t. the function and predicate
symbols defined in an interpretation I:
Reflectivity: ∀x, x = x;
Symmetry: ∀x∀y, x = y ⇒ y = x
Transitivity: ∀x∀y∀z, (x = y ∧ y = z) ⇒ x = z
Congruence on functions: For every function symbol f of arity n, for every
1 ≤ i ≤ n we have
∀x1 . . . ∀xn ∀y, xi = y ⇒
f (x1 , . . . , xi−1 , xi , xi+1 , . . . , xn ) = f (x1 , . . . , xi−1 , y, xi+1 , . . . , xn )
Congruence on atoms: For every predicate symbol p of arity n, for every
1 ≤ i ≤ n we have
∀x1 . . . ∀xn ∀y, (xi = y ∧ p(x1 , . . . , xi−1 , xi , xi+1 , . . . , xn )) ⇒
p(x1 , . . . , xi−1 , y, xi+1 , . . . , xn )
This set of equations is called K and was given by [53]. While it is complete,
the Congruence on atoms clauses can be resolved with any clause. The
ensuing combinatorial explosion makes it an unpractical choice for automated
theorem proving. Since it is practical to reason modulo these equations, given
a first-order theory T we denote I |== T the fact that I |= T ∪ K.
4.7.2 Unification Modulo an Equational Theory
A fruitful research direction is to consider extensions of the resolution rule, such
as paramodulation [216] and its superposition [44, 141] variant, that take into
account the properties of the equality predicate. However in many cases the
clauses that contain the equality predicate contain only one positive literal.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-67-320.jpg)
![68 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
Example 14. In order to model lists one can use one nullary function symbol
“elist”, and one binary function symbol “cons”. The usual list operations “head”
and “tail” can be modeled by the clauses:
∀x∀l, head(cons(x, l)) = x
∀x∀l, tail(cons(x, l)) = l
Definition 15. (Equational theory) An equational theory E is a conjunction
of clauses ∀x1 . . . ∀xn , t = s where t and s are terms with variables among the
x1 , . . . , x n .
Plotkin [181] was the first to notice that when reasoning modulo an equa-
tional theory it suffices to consider the terms in the Herbrand’s domain modulo
the equations. As a consequence the only adaptation needed w.r.t. to our pre-
sentation of first-order logic is to consider unification modulo the equalities in
the equational theory.
Definition 16. (E-unifiers) Let E be an equational theory. We say that two
terms t and s are E-equal, and denote s =E t, if E |== t = s. We say that a
substitution σ is a E-unifier of s and t if E |== tσ = sσ.
We say that two terms that have a E-unifier are E-unifiable. We extend the
notion of unifier to conjunctions of equations as follows.
Definition 17. (Unification systems) Let E be an equational theory. An E-
?
Unification system S is a finite set of equations denoted by {ui = vi }i∈{1,...,n}
with terms ui , vi ∈ T (F, X ). It is satisfied by a substitution σ, and we note
σ |= E S, if for all i ∈ {1, . . . , n} ui σ =E vi σ.
One easily proves that the definition of unifiers in Section 4.6.3 correspond
to the case where the equational theory E is an empty set of clauses. As in
Section 4.6.3 we denote ΣE (t, t ) the set of unifiers of t and t . Also, we say that
a substitution σ is more general than a substitution τ modulo E, and denote
σ E τ if there exists a substitution θ such that for every variable x we have
mgt
xσθ =E xτ .
Example 15. Consider the equational theory E = {f (x, f (y, y)) = x}. Then
the substitution σ = {x → f (y, z)} is more general than the substitution τ =
{z → f (v, v), x → y} since for all variable w we have wσθ =E wθ.
As Example 15 demonstrate we can have two unifiers that instantiate one
another but are not a renaming one of the other, as was the case in Lemma 4.10.
Since the relation between unifiers that are instances one of the other is more
complex than in the case of the empty theory, we introduce the notion of com-
plete set of unifiers.
Definition 18. (Complete set of unifiers) Let E be an equational theory and
t, t be two terms. We say that a subset S of ΣE (t, t ) is a complete set of unifiers
of t and t if, for every substitution σ ∈ ΣE (t, t ) there exists a substitution τ ∈ S
and a substitution θ such that τ θ =E σ.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-68-320.jpg)

![70 CHAPTER 4. FUNDAMENTALS OF FIRST-ORDER LOGIC
Definition 20. Let E be an equational theory and t, t be any two E-unifiable
terms. We say that:
• E is nullary if mguE (t, t ) does not necessarily exist;
• If mguE (t, t ) necessarily exists, we say that:
– E is unary if mguE (t, t ) must be a singleton;
– Otherwise, E is finitary if mguE (t, t ) must be a finite set;
– Otherwise, E is infinitary if mguE (t, t ) can be a infinite set;
Also, unification systems are classified w.r.t. the terms occuring in them.
Let E be an equational theory in which the non-variable symbols occurring in
the equations of E are in a signature F. We say that a unification system S is:
Elementary if the terms occurring in S are in T (F, X ) ;
with constants if the terms occurring in S are built from symbols in S, vari-
ables, and nullary symbols not in F;
General if the terms occurring in S are built from symbols in S, variables, and
arbitrary symbols not in F.
Accordingly we say that a symbol occurring in a term t is free (w.r.t. the
equational theory E defined over the signature F) if it is not a symbol in F. In
the rest of this document and when reasoning modulo an equational theory we
denote C a denumerable set of free constants, i.e. nullary symbols not occurring
in any equation of E.
4.7.3 Some properties of E-unification systems.
There exists few properties that are common to all equational theories. However
some of them are instrumental in our work on the analysis of cryptographic
protocols, and are presented here. In the rest of this section, we assume that
E is an equational theory defined by equations over a signature F, that C is
a denumerable set of constants not occurring in F, and that T (F, X ) and
T (F) denote respectively the sets of terms and of ground terms built over the
signature F ∪ C.
Existence of a convergent rewriting relation
We shall first introduce the notion of ordered rewriting [100]. Let < be a sim-
plification ordering on T (F) 5 assumed to be total on T (F) and such that the
minimum for < is a constant cmin ∈ C. Given a possibly infinite set of equa-
tions O on the signature T (F) we define the ordered rewriting relation →O
by s →O s iff there exists a position p in s, an equation l = r in O and a
substitution τ such that s = s[p ← lτ ], s = s[p ← rτ ], and lτ > rτ .
5 by definition < satisfies for all s, t, u ∈ T (F ) s < t[s] and s < u, t|p = s imply t < t[p ← u]](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-70-320.jpg)
![4.7. FIRST-ORDER LOGIC WITH EQUALITY 71
It has been shown (see [100]) that by applying the unfailing completion
procedure [123] to a set of equations E one can derive a (possibly infinite) set of
equations O such that:
1. the congruence relations =O and =E are equal on T (F).
2. →O is convergent (i.e. terminating and confluent6 ) on T (F).
We shall say that O is an o-completion of H.
The relation →O being convergent on ground terms we define (t)↓O as the
unique normal form of the ground term t for →O . Given a ground substitution
σ we denote by (σ)↓O the substitution with the same support such that for all
variables x ∈ Supp(σ) we have x(σ)↓O = (xσ)↓O . A substitution σ is normal if
σ = (σ)↓O .
Replacement
An important property of E-unification systems, whose proof can be found
in [70], is the following replacement property. Given terms u, v, t, we denote
by tδu,v the parallel replacement of all occurrences of u by v in t. Given a sub-
stitution σ we denote by σδu,v the substitution such that x(σδu,v ) = σ(x)δu,v
for every variable x.
Remark 1. A replacement behaves like a substitution, with the main difference
being that it replaces a term, and not a variable, with another term. The use
of replacement instead of substitutions is mandatory from a technical point of
view: unfailing completion provides one with a convergent rewriting system on
ground terms when they are totally ordered with a simplification ordering. Non-
ground terms are generally speaking never totally ordered by a simplification
ordering, the rationale being that two distinct variables cannot be ordered by a
liftable ordering (proof left to the reader).
Let us first extend the notion of free constant w.r.t. an equational theory E.
Let T be a set of terms. We say that a term t is bound by σ in T whenever there
exists r ∈ T X such that rσ =∅ t. A term t is σ-free in T if it is not bound by
σ in T . We say that t is bound in T if there exists σ such that t is bound by σ
in T . Otherwise we say that t is free in T . Given an equational theory E let us
define :
TE = Sub(r) ∪ Sub(s)
r=s∈E
We say that a term t is bound (resp. free) in E if t is bound (resp. free) in TE .
Given a term t and an equational theory E we call the factors of t, and denote
Factors(t), the set of maximal strict subterms of t which are free in E. First let
us note an important result that has a trivial proof.
6 if two terms t , t are equal modulo =
1 2 O there exists a term t3 reachable from both t1 and
t2 by a sequence of ordered rewriting](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-71-320.jpg)

![4.7. FIRST-ORDER LOGIC WITH EQUALITY 73
Proof. By contradiction let us assume the set Ω of couples (r, s) which are
counterexamples to the lemma is not empty. Since for each (r, s) ∈ Ω we
have r =E s and since E is a congruence, let µ(r, s) be the minimal number of
equations in E to apply to rewrite r into s. Since Ω cannot contain a couple
(r, r) (for which the lemma would be trivially true) the minimum of µ over Ω
is strictly positive. This minimum cannot be greater than or equal to 2 for
otherwise we would have r =1 r =E s—where =1 denotes the equality after
E E
the application of exactly one equation in E—with r = r and r = s, and thus
either rδt,u =E r δt,u or r δt,u =E sδt,u . We thus have both µ(r, r ) < µ(r, s) and
µ(r , s) < µ(r, s). Since at least one of these couples must be in Ω we contradict
the minimality of µ(r, s).
Thus if Ω = ∅ there exists two terms r, s whose factors are in normal form,
a term t free in E, and a term u such that r =1 s but rδt,u =E sδt,u . We have:
E
• We recall that t is a free term in E in normal form. Thus by definition of
factors every occurrence of t in r, s must be a subterm of a factor;
• Let g = d be the equation in E applied at position p in r that yields
the term s. I.e. there exists a substitution σ such that r|p = gσ, and
s = r[p ← dσ]. Since t is a free term in E it is free in Sub(g, d);
• Thus by Lemma 4.21 we have (gσ)δt,u = g(σδt,u and (dσ)δt,u = d(σδt,u .
• Thus the same equation can be applied at the same position between rδt,u
and sδt,u with the substitution σδt,u , and therefore rδt,u ==E sδt,u .
• This contradicts the membership of the couple (r, s) in Ω.
Thus we must have Ω = ∅, which proves the lemma.
When studying terms modulo an equational theory an interesting point to
consider is the conditions under which one can “combine” Lemmas 4.21 and 4.22
to obtain a replacement lemma for solutions of a unification system modulo an
equational. The main difficulty here is that Lemma 4.22 assumes that the
factors are already in normal form. However when one considers an arbitrary
set of equations it is not true, in general, that a bottom-up rewriting strategy is
complete. One way to recover completeness for such a strategy is to use ordered
rewriting with the o-completion of the equational theory. The complete proof
of this lemma can be found in [70, 76].
Lemma 4.23. For any equational theory E, if a E-unification system S is sat-
isfied by a substitution σ, and c is any constant in C away from S, then for any
term t, σδc,t is also a solution of S.
The proof of Lemma 4.23 consists in first analyzing the unfailing comple-
tion algorithm to prove that no free constant occur in the equations of ordered
completion of a theory E, and thus that c free in E implies that c is free in any
o-completion of E. One then considers a sequence of ordered rewriting transi-
tions from a term t to its normal form and prove that rewriting commutes with
the replacement δc,t .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-73-320.jpg)



![Chapter 5
Refinements of Resolution
Refinements of resolution are restrictions on the possible fac-
torization or resolution inferences between clauses, as well as
simplifications on the set of clauses under scrutiny. The first
motive for the introduction of these restrictions was practical as
it accelerated the search of the empty clause (see the discussion
in [95]). It later turned out that in some cases resolution with
refinements starting from a theory T terminates with a set of
clauses T ’ that is not unsatisfiable. These sets are called sat-
urated w.r.t. the refinement adopted, and can be employed to
decide whether the theory T entails a sentence ϕ [112].
The goal of this chapter is to present the refinement proposed
in collaboration with Mounira Kourjieh. To this end we do not
provide an overview of all existing refinements as the one in [18]
but instead to focus on the ones related to our own.
5.1 Ordered Resolution
5.1.1 Liftable orderings
While resolution is much more efficient than the naive algorithm to prove that
a finite set of clauses is unsatisfiable, its degree of non-determinism still makes
it unfit as soon as the theory under scrutiny has more than a few clauses each
with few literals. In Chapter 4 we have proved the following theorem on finite
sets of ground clauses.
Theorem 4.6, p. 59. Let S be a finite set of ground clauses over the atoms
ξ1 , . . . , ξk . Then S is unsatisfiable if, and only if, Resgr (ξ1 , . . . Resgr (ξk , S))
contains the empty clause.
We remark that the atoms ξ1 , . . . , ξk can be chosen in an arbitrary order.
Thus let us assume a is an arbitrary ordering over the atoms in the Herbrand
universe of a theory T .
77](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-77-320.jpg)

![5.1. ORDERED RESOLUTION 79
Post-ordered factorization: If l1 ∨ l2 ∨ C and ξi is the atom occurring in li
for ı ∈ {1, 2}, then if σ = mgu(l1 , l2 ), and if both ξ1 σ and ξ2 σ are maximal
w.r.t. the atoms occurring in Cσ, then l1 σ ∨ Cσ is a post-ordered factor
of l1 ∨ l2 ∨ C;
Post-ordered resolution: If ξ1 ∨ C1 and ¬ξ2 ∨ C2 are two clauses such that
σ = mgu(ξ1 , ξ2 ) and ξ1 σ (resp. ξ2 σ) is maximal w.r.t. the atoms occurring
in C1 σ (resp. C2 σ), then (C1 ∨ C2 )σ is a post-ordered resolvent of ξ1 ∨ C1
and ¬ξ2 ∨ C2 .
We call post-ordered resolution the iterated application of the post-ordered fac-
torization and resolution rules.
We note that whenever a post-ordered factorization or resolution rule can be
applied on one or two clauses, then factorization or resolution can be applied on
the same set of clauses and yields the same resolvent. Thus Theorem 4.8 implies
that if an iterated application of the post-ordered factorization and resolution
rules on a set of clauses S reaches the empty clause [ ], then S is unsatisfiable.
However, since we have restricted the possible applications of factorization and
resolution the completeness part of Theorem 4.8 is not necessarily true. It is
however preserved thanks to Corollary 5.1 and Lemma 5.1.
Theorem 5.1. (Completeness of post-ordered resolution) If S is an unsatisfi-
able set of clauses there exists a finite sequence of application of post-ordered
factorization and resolution starting from S reaching the empty clause [ ].
Proof. By Theorem 4.4 S unsatisfiable implies that there exists an unsatisfiable
finite set Sg of ground instances of clauses in S. By definition of the simula-
tion relation we have Sg S. By Corollary 5.1 there exists a finite sequence
of ground factorization and resolution rules starting from Sg that reaches the
empty clause such that, for each rule application:
ground factorization lg ∨ lg ∨ Cg : let ξg be the atom occurring in lg and ξg
an atom occurring in Cg . We have ξg a ξg ;
ground resolution between ξg ∨ Cg and ¬ξg ∨ Cg : for every atom ξg occur-
ring in Cg or Cg we have ξg a ξg .
Let Sg be a finite ground unsatisfiable set of clauses and S be such that
Sg S . Let us prove that for every application with the above restrictions
of the ground factorization or resolution rule on Sg there exists a post-ordered
factorization or resolution rule applicable on S that preserves the simulation.
Factorization. Assume lg ∨ lg ∨ Cg ∈ Sg , let ξg be the atom occurring in
l, and ξg be an atom occurring in Cg . Since S simulates Sg there exists a
clause l1 ∨ l2 ∨ C ∈ S and a ground substitution σ such that l1 σ = l2 σ = lg and
Cσ = Cg . By Lemma 4.18 there exists θ = mgu(l1 , l2 ) and a ground substitution
τ such that ((l1 ∨ C)θ)τ = lg ∨ Cg . By Lemma 5.1 the atom occurring in l1 θ
is maximal for a w.r.t. the atoms occurring in Cθ. Thus (l1 ∨ C)θ is a post-
ordered factor of a clause in S that simulates lg ∨ Cg .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-79-320.jpg)
![80 CHAPTER 5. REFINEMENTS OF RESOLUTION
Resolution. Assume ξg ∨ C, ¬ξg ∨ C ∈ Sg , and that ξg is maximal w.r.t.
the atoms occurring in C and C . Since Sg S there exists by Lemma 4.17
ξ1 ∨ C1 , ¬ξ2 ∨ C2 ∈ S and two substitutions θ and τ such that:
• ((ξ1 ∨ C1 )θ)τ = ξg ∨ C and ((¬ξ2 ∨ C2 )θ)τ = ¬ξg ∨ C ;
• ξ1 θ = ξ2 θ.
By Lemma 5.1 ξ1 θ is maximal w.r.t. the atoms occurring in C1 θ and C2 θ, and
thus (C1 ∨ C2 )θ is a post-ordered resolvent of ξ1 ∨ C1 and ¬ξ2 ∨ C2 ∈ S that
simulates C ∨ C .
Thus if S is unsatisfiable there exists a finite sequence of post-ordered factor-
ization and resolution rule applications that reaches a set of clauses containing
[ ].
Pre-ordered Resolution
When implementing a resolution theorem prover, it can be costly to test after
each tentative factorization or resolution whether the factored or resolved atom
is maximal. Thus one sometimes prefers to compute the set of maximal atoms
in a clause only once, and to compute the ordered factors and resolvents w.r.t.
the maximal atoms found. This schema corresponds to the two following rules
applicable on a set of clauses S given a liftable ordering a :
Pre-ordered factorization: If l1 ∨ l2 ∨ C and ξi is the atom occurring in li
for ı ∈ {1, 2}, then if σ = mgu(l1 , l2 ), and if both ξ1 and ξ2 are maximal
w.r.t. the atoms occurring in C, then l1 σ ∨ Cσ is a pre-ordered factor of
l1 ∨ l2 ∨ C;
Pre-ordered resolution: If ξ1 ∨ C1 and ¬ξ2 ∨ C2 are two clauses such that
σ = mgu(ξ1 , ξ2 ) and ξ1 (resp. ξ2 ) is maximal w.r.t. the atoms occurring
in C1 (resp. C2 ), then (C1 ∨ C2 )σ is a pre-ordered resolvent of ξ1 ∨ C1 and
¬ξ2 ∨ C2 .
We call pre-ordered resolution the iterated application of the pre-ordered fac-
torization and resolution rules.
We note that every pre-ordered factorization rule application is a factor-
ization rule application, and every pre-ordered resolution rule application is a
resolution rule application. Thus the soundness of resolution implies the sound-
ness of pre-ordered resolution.
Also we note that since the ordering is liftable, every post-ordered factor-
ization rule application is a pre-ordered factorization rule application, and that
every post-ordered resolution rule application is a pre-ordered resolution rule
application. Thus the completeness of post-ordered resolution implies the com-
pleteness of pre-ordered resolution.
Theorem 5.2. (Soundness and completeness of pre-ordered resolution) A set
S of clauses is unsatisfiable if, and only if, there exists a finite sequence of pre-
ordered factorization and resolution rule application starting from S reaching a
set of clauses containing [ ].](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-80-320.jpg)
![5.2. PREVIOUS WORK ON ORDERED SATURATION 81
Conclusion
These completeness theorems have first been proved in [153, 154, 135] using
either the inverse method [153, 154] or semantic trees [135]. Another approach
of note to prove completeness consists in building explicitly a Herbrand inter-
pretation [18]. The argument we have employed is a variation of the one in [135]
but without the machinery of semantic trees. In particular we use an ordering
on the atoms, whereas [153, 154] employs an ordering on the literals. The major
difference with [135] is that we first obtain a finite set of atoms from Herbrand
Theorem and then consider an ordering on this set, whereas Kowalski and Hayes
obtain this set of atoms once an infinite semantic trees is built.
5.2 Previous Work on Ordered Saturation
When a resolvent C between two clauses of S is added to S we obtain an
equisatisfiable set of clauses. Thinking in terms of procedures, we however want
to have more than mere equisatisfiability, i.e. ensure that some sort of progress
happens when the resolvent is added. This notion of progress was formalized by
Bachmair and Ganzinger in [17] by using an ordering on clauses. They remarked
that the resolvent obtained by post-ordered resolution between two clauses was
smaller, for a well-founded ordering on clauses based on the ordering on atoms,
than one of the premises. This remark lead to a criterion that permits one to
remove a clause from a set of clauses when it does not progresses. Later this
result was built upon in [26] by defining a clause C to be redundant in S if it is
entailed by a set of instances of clauses in S which are each smaller than C.
Let a be a atom ordering total on ground terms and compatible with a term
ordering t . Equipped with this definition Basin and Ganzinger have proved
that a set S of clauses saturated by post-ordered resolution w.r.t. a is local
w.r.t. a if S is reductive w.r.t. a and t , i.e. if for each ground instance C
of a clause in S, if A is maximal is maximal in C, then for each atom B in C,
for each term t occurring in B, there exists a term s occurring in A such that
t t s.
As a consequence of this GivanM92 result w.r.t. a total, well-founded atom
ordering compatible with a term ordering t , Basin and Ganzinger proved that
if a set of clauses S is reductive w.r.t. a and t and if, for every ground
atom A there exists only a bounded number of ground atoms smaller
than A, then the ground entailment problems are decidable for S, i.e. the
function:
Sat if S |= C
entailment(S, C) =
Unsat Otherwise
can be computed. The last part of the proof is trivial: by GivanM92 and the
boundedness assumption if S |= C then there exists a refutation of ¬C ∪ S in
which only atoms smaller for a than those occurring in C occur. It then suffices
to form all the ground instances of the clauses in S that satisfy this criterion.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-81-320.jpg)
![82 CHAPTER 5. REFINEMENTS OF RESOLUTION
This construction yields a finite set of ground clauses whose unsatisfiability can
be decided.
Introduction to our contribution. In contrast with this approach, I have
proposed with Mounira Kourjieh an extension to finite sets of clauses of our
work on saturated deduction systems (presented in Chapter 8. We removed the
assumptions that a and t are total on ground atoms and terms1 , and replaced
reductiveness and compatibility by the (admittedly more restrictive) liftability
of the atom ordering and the condition that A a B implies Var(A) ⊆ Var(B).
But more importantly, we removed the boundedness assumption, i.e. we do
not assume that for every ground atom A there exists only a bounded
number of ground atoms smaller than A. Having replaced totality on
ground terms, reductiveness and boundedness2 assumptions by liftability and
variable inclusion, we prove that if a set of clauses is saturated by ordered
resolution w.r.t. a suitable ordering a then its ground entailment problem
is decidable. We present this approach in the rest of this chapter. The short
version of this result was presented at LPAR 16, in Dakar.
5.3 Decidability of ground entailment problems
5.3.1 Motivation
In [26, 25], D. Basin and H. Ganzinger showed that the order saturation of a set
S of Horn clauses w.r.t. a well-founded and liftable ordering is not sufficient to
obtain the decidability of the ground entailment problem for S, as demonstrated
by the following example.
Example 17. (Uwe Waldmann, presented in [26, 25]) Let S be an arbitrary set
of clauses and C be a ground clause. Construct S and C such that S consists
of the set of clauses q() ∨ C such that C ∈ S, and let C = q() ∨ C . Choose
any ordering such that q() is the maximal atom, Thereby implying that every
proof of S |= C is order local. The ground entailment problem problem S |= C
is trivially reducible to S |= C . Since the former is in general undecidable so
is the latter problem. Thus there exists order local sets of Horn clauses whose
ground entailment problem is undecidable.
Let a be an atom ordering. We note that in Example 17 it is possible to
choose the ordering a to be well-founded and liftable. Let us prove that if
one assumes in addition to liftability and well-foundedness of a that A a B
implies Var(A) ⊆ Var(B) then ground entailment problems become decidable.
As usual we assume a functional signature F and a relational signature P,
and denote T (F, X ) the set of terms over F, and T (F) the Herbrand domain
1 As remarked by Basin and Ganzinger in [26], the totality assumption does not lose gen-
erality when the ordering is bounded, as one can then try all the total extensions of the atom
ordering. This construction is however not effective if the boundedness condition is removed.
2 I insist given that a majority of the reviewers of our submissions of this result insist that
it is entailed by the one by Basin and Ganzinger, or that the proof is the same.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-82-320.jpg)
![5.3. DECIDABILITY OF GROUND ENTAILMENT PROBLEMS 83
associated to the signature F. Given a clause C we denote atoms(C) the set of
the atoms occurring in C, called its domain. We extend the notion of domain
to sets of clauses as expected with atoms(S) = ∪C∈S atoms(C). We say that a
clause is a unit clause if it contains only one literal. Given a clause C = l1 ∨. . .∨lk
we denote ¬C the set of unit clauses {¬l1 , . . . , ¬lk }.
Ground entailment problem. We are interested in this section in giving
conditions such that it is possible to decide whether a ground clause C is a
logical consequence of a set of clauses S. Let us now formally define this problem.
Given a set of clauses S, the ground entailment problem for S is the following
decision problem:
Ground EntailmentS (C)
Input: a ground clause C
Output: Sat if and only if S |= C
Example 18. Let us consider the ordering on atoms defined by the closure
by stability of the ordering p(x, t(x, y)) a p(s(x), y), for any term t(x, y) having
variables x and y. One easily sees that this atom ordering is well-founded (and
bounds the length of a chain starting from an atom p(t1 , t2 ) by the size of t1 )
and that A a B implies Var(A) ⊆ Var(B). The quantification over any term
t however implies that an atom may have an infinite number of atoms smaller
than itself.
5.3.2 Locality and Saturation
Our presentation follows the historical development of first the notion of (sub-
term) GivanM92 as introduced by GivanM92 in [118, 118] for sets of Horn
clauses, and then the notion of order GivanM92 as defined by Basin and Ganzinger
in [26, 25].
Subterm GivanM92. GivanM92’s work [118] is based on Horn clauses. The
local entailment of a clause C by a set of clause S, denoted S |=l C, means
that there exists a finite set S g of ground instances of clauses in S such that
S g , ¬C is unsatisfiable and such that every term occurring in a clause in S g is
a subterm of some term occurring in C.
A set of Horn clauses S is subterm local if for every ground Horn clause C,
we have S |= C if and only if S |=l C. It is proved in [118] that if a set S of
Horn clauses is finite and subterm local then its ground entailment problem is
decidable in polynomial time.
Order GivanM92. Basin and Ganzinger [26, 25] generalized GivanM92’s
work by allowing any strict well-founded term ordering t over terms, and full
(not Horn) clauses. Again, a set of clauses S is said to locally entail a ground](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-83-320.jpg)
![84 CHAPTER 5. REFINEMENTS OF RESOLUTION
clause C, which is denoted S |= t C, whenever there exists a finite set S g of
ground instances of clauses in S such that S g , ¬C is unsatisfiable and such that
every term occurring in a clause in S g is smaller for t than a term occurring
in C.
A set of clauses S is order local for the term ordering t whenever for every
ground clause C we have S |= C iff S |= t C.
Given a term ordering t we can have at the same time—as e.g. for lexi-
cographic or recursive path ordering—that t is well-founded and is such that
for some ground term t there exists an infinite set of terms t such that t t t.
We remark that in this case order GivanM92 does not imply the decidability of
ground entailment problems.
However it is often sufficient to consider term orderings of finite complexity.
A term ordering t is said to be of complexity f, g whenever for each clause of
size n (the size of a term is the number of nodes in its dag representation, and
the size of a clause is the sum of sizes of its terms) there exists O(f (n)) terms
that are smaller or equal (under t ) to a term in the clause, and that may be
enumerated in time g(n). It is easy to see that if t is of complexity f, g then
each ground term has finitely many smaller terms that may be enumerated in
finite time [26, 25].
Theorem 5.3. (Basin, Ganzinger [26, 25]) If S is a set of Horn clauses that is
order local with respect to a term ordering t of complexity f, g then the ground
entailment problem for S is decidable.
The work we present can be considered as a weakening of the conditions
under which order GivanM92 implies decidability. On the one hand Basin and
Ganzinger mandate that the atom ordering must be total and well-founded on
ground atoms, compatible with a term ordering of finite complexity, and that
the set of clauses has to be reductive w.r.t. the atom and term orderings.
On the other hand we do not consider the ordering on terms and assume that
the ordering on atoms is well-founded, liftable and is such that A a B implies
Var(A) ⊆ Var(B).
5.3.3 Saturation
As specified above, we consider an atom ordering a which is liftable, well-
founded and such that A a B implies Var(A) ⊆ Var(B).
Rewriting atoms
Definition Rewriting systems are usually defined over terms and are employed
to model equational theories. In contrast with this standard setting, we consider
rewriting systems on atoms to define finitely branching orderings on atoms.
Definition 22. A rewriting system on atoms R based on a is a set of couples
(L, R) where L and R are atoms with R a L. Each couple (L, R) is called a
rewriting rule and is denoted L → R.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-84-320.jpg)



![88 CHAPTER 5. REFINEMENTS OF RESOLUTION
Saturation procedure. The procedure starts from the couple (S, R(S)) and
is iterated until a fixed-point is reached. Each step is a transformation (S1 , R1 ) →
(S2 , R2 ) constructed as follows:
• Let C1 , C2 be two clauses in S1 , and C be the conclusion of an ordered
resolution inference on C1 , C2 where the substitution employed is σ and
the resolved atom is Aσ.
• Three cases are possibles:
Non-maximality: If Aσ is not maximal for a in the atoms of C1 σ, C2 σ
then S2 = S1 and R2 = R1 ∪ R({C1 σ, C2 σ});
Redundancy: If S1 C↓R1 C, then S2 = S1 and R2 = R1 ;
Discovery: Otherwise a new clause useful for establishing local proofs
has been discovered. In this case we set S2 = S1 ∪ {C} and R2 =
R1 ∪ R(C).
A sequence of steps is fair [18] if every possible inference by a priori ordered
resolution is eventually performed.
Definition 27. (Result of the saturation procedure) Given a finite set of clauses
S and an atom ordering a we denote min a (S) a couple (S , R) obtained by
a fair sequence of steps by the saturation procedure in case it terminates.
First let us prove that the procedure actually constructs a saturated set of
clauses.
Proposition 5.1. Let S be a finite set of clauses and a be a liftable, well-
founded atom ordering such that A a B implies Var(A) ⊆ Var(B).
If the saturation procedure terminates on S and min a (S) = (S , R) then S
is R-saturated.
Proof. Assume there exists two clauses C1 , C2 ∈ S and a substitution σ such
that the inference C1 σ, C2 σ C is not R-redundant. In the saturation algo-
rithm it thus falls into one of the non-maximality or discovery cases.
non-maximality: Assume the resolved atom A is not maximal in the atoms of
C1 σ, C2 σ. Then this inference is not an inference by a posteriori ordered
resolution. It is thus R(C1 σ) ∪ R(C2 σ)-redundant. Since it is not redun-
dant we must have R(C1 σ) ∪ R(C2 σ) ⊆ R. This implies that (S , R) is
not a result of the saturation algorithm.
discovery: If (S , R) were a result of the saturation algorithm we would have
had C ∈ S , which would trivially (for any atom rewriting system) have
implied that the inference was redundant in S.
As a consequence every inference between two clauses of (S , R) must be R-
redundant. We leave the conditions on R to the reader. Thus the set S is
R-saturated by Definition 26.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-88-320.jpg)
![5.3. DECIDABILITY OF GROUND ENTAILMENT PROBLEMS 89
5.3.4 Decidability of the ground entailment problem
We consider in this section a R-saturated set of clauses S. In spite of the
differences in definitions we prove that as in [26, 25] saturation implies GivanM92
in our sense. The spirit of the proof is a combination of those in [59, 26, 25].
Proposition 5.2. Let S be a R-saturated set of clauses, and C be a ground
clause. Then S |= C implies S C↓R C
Proof. Assume that S |= C, and let T be the set of unsatisfiable finite sets of
ground instances of S ∪ ¬C. By Herbrand’s Theorem we know that T = ∅. Let
Tmin ⊆ T be a set of finite sets T such that the set atoms(T ) ↓R atoms(C) ↓R
is minimal for the extension on sets of atoms of the ordering a . If this set of
atoms is empty then we are done as each T ∈ Tmin is then an unsatisfiable finite
set of ground instances of S ∪ ¬C in which all atoms are in C ↓R .
Otherwise for any T ∈ Tmin the set of atoms in T is finite and therefore
atoms(T ) ↓R is also finite by Lemma 5.2. Thus we can consider a maximal
element A (the same for all T in Tmin ) in atoms(T ) ↓R C ↓R . Since A is
maximal we also have that A is an atom occurring in T for each T ∈ Tmin .
Claim 4. For any T ∈ Tmin the atom A is maximal in atoms(T ) for the ordering
R.
Proof of the claim. By contradiction if this were not the case there would
exist B ∈ T with A R B. Since A is maximal in T ↓R C ↓R we would
have that B would not be in this set. Since B ∈ atoms(T ) this would
imply B ∈ C ↓R . By definition we would then have A ∈ C ↓R , which
would contradict A ∈ T ↓R C ↓R . ♦
Let T be in Tmin , and let Leaves+ be the set of clauses in T that contain
A
the atom A, and Leaves− be the subset of clauses of T that do not contain A.
A
Let us consider the set Leaves of all possible conclusions of resolution on A
between clauses in Leaves+ . The set of ground clauses Leaves ∪ Leaves− is also
A A
unsatisfiable.
Claim 5. Each clause CA ∈ Leaves+ is an instance with a substitution σ of a
A
clause CA ∈ S that has a maximal atom As for a with As σ = A.
s
Proof of the claim. By definition CA is either an instance of a clause
in S or of a clause in ¬C. Since A is not an atom occurring in C the
latter case is excluded. Thus there exists CA ∈ S, an atom As ∈ CA , and
s s
s s s
a substitution σ such that A σ = A and CA σ = CA . Finally if A is not
s
maximal for a in CA then it is not maximal for R and thus A cannot
be maximal for R in the atoms of CA . This would contradict the fact
that A is maximal for R among the atoms occurring in T . ♦
Thus every resolution on A between clauses in Leaves+ is an instance with
A
substitution σ of an a priori ordered resolution inference between two clauses
C1 and C2 of S. Let C3 ∈ Leaves be its conclusion. Since S is R-saturated](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-89-320.jpg)
![90 CHAPTER 5. REFINEMENTS OF RESOLUTION
each such inference is redundant. We note that A maximal in atoms(T ) for R
and the fact that S is saturated (second point of the ordering condition) for
R imply that A cannot be smaller for R than an atom in C3 . Thus for each
conclusion C3 we can define a set §(C3 ) which is either:
g
• the singleton {C3 } if C3 is an instance of a clause C3 ∈ S;
g
• or a set SC3 of instances of clauses of S whose atoms are in C3 ↓R ∪A ↓−
R
that entails C3
The set of ground clauses S g = Leaves− ∪ C3 ∈Leaves §(C3 ) is unsatisfiable.
A
By construction we have atoms(Sg ) ↓R ⊆ (atoms(T ) {A}) ↓R ∪A ↓− . Since
R
A is maximal in atoms(T ) for R and A is not in C ↓R this implies that
atoms(Sg ) ↓R C ↓R a atoms(T ) ↓R C ↓R . This contradicts the fact that T
is in the set of minimal consequences Tmin .
Theorem 5.4. Let a be a well-founded, liftable atom ordering such that for
any two atoms A and B we have A a B implies Var(A) ⊆ Var(B). Let S be a
set of clauses, and assume that saturation terminates using the atom ordering
a.
Then the ground entailment problems for S are decidable.
Proof. Let (S , R) be the result of the saturation of S with the ordering a .
Since S ⊆ S for every ground clause C we have S |= C implies S |= C.
Conversely since all clauses in in S S are logical consequences of S we have
S |= C implies S |= C. By Proposition 5.3 S |= C is decidable, hence so is the
equivalent problem S |= C.
We have already noted that S C↓R C trivially implies S |= C. As a
consequence of Lemma 5.4 and of Proposition 5.2 we thus have the following
proposition.
Proposition 5.3. If S is a R-saturated set of clauses then the ground entail-
ment problems for S are decidable.
Our final theorem is a self-contained re-formulation of the above proposition
using the initial set of clauses.
Theorem 5.4. Let a be a well-founded, liftable atom ordering such that for
any two atoms A and B we have A a B implies Var(A) ⊆ Var(B). Let S be a
set of clauses, and assume that saturation terminates using the atom ordering
a.
Then the ground entailment problems for S are decidable.
5.3.5 Conclusion and future works
We have presented in this section an extension of a result by Basin and Ganzinger [26,
25]. The relaxation of the hypothesis on the ordering may lead to a further ex-
tension for resolution modulo an equational theory [124, 168, 209]. We believe](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-90-320.jpg)
![5.3. DECIDABILITY OF GROUND ENTAILMENT PROBLEMS 91
the technique employed can be extended to add a reflexivity or transitivity
axiom to an already saturated theory. Also, we thank Chris Lynch [150] for
having pointed to us (by giving a counter-example) that the method cannot be
extended as is to superposition. Finally we believe that a consequence of our
proof is that saturated theories are complete for contextual deduction [43, 167],
which may help in the resolution of [101], though further work is needed to
confirm this conjecture.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-91-320.jpg)



![Chapter 6
Symbolic models for
Cryptographic Protocols
We begin in this chapter the presentation of the core of our
work on the symbolic analysis of cryptographic protocols. We
first associate to each narration a logical model called an active
frame. Though it is not strictly speaking a first-order theory
as are the protocol models in [126], it nonetheless captures the
essential message exchange features of cryptographic protocols.
From these active frames we can derive the constraint systems
routinely employed [8, 161, 55] to model a finite execution of a
protocol. We then present symbolic derivations, a refinement of
active frames.
The compilation process described in this section was published
in [74]. We have included it in this document to have a self-
contained presentation of our work. We then present a more
refined model of the internal computations of a protocol partic-
ipant, the symbolic derivations, which was originally introduced
in [65].
6.1 Introduction
Cryptographic protocols are designed to prescribe message exchanges between
agents in hostile environment in order to guarantee some security properties
such as confidentiality. There are many apparently similar ways to describe a
given security protocol. However one has to be precise when specifying how
a message should be interpreted and processed by an agent since overlooking
subtle details may lead to dramatic flaws. The main issues are the following:
• What parts of a received message should be extracted and checked by an
agent?
95](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-95-320.jpg)
![96CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
• What actions should be performed by an agent to compute an answer?
These questions are often either partially or not at all adressed in common
protocol descriptions such as the protocol narrations 2.1.3, p. 18 such as the
Needham-Schroeder Public Key protocol [166] which is conveniently specified
by the following text:
A→B:encp ( A, Na , KB )
B→A:encp ( Na , Nb , KA )
A→B:encp (Nb , KB )
where
−1
A knows A, B, KA , KB , KA
−1
B knows A, B, KA , KB , KB
Protocol narrations are also a textual representation of Message Sequence Charts
(MSC), which are employed e.g. in RFCs (see Subsection 2.1.2, p. 17). We claim
that all internal computations specified in RFCs, and more generally most such
annotations, can be computed automatically from the protocol narration. Our
goal in this chapter is to give an operational semantics to—or, equivalently, to
compile—protocol narrations so that internal actions (excluding e.g. storing a
value in a special list for a use external to the protocol) are described.
Related works Although many works have been dedicated to verifying cryp-
tographic protocols in various formalisms, only a few have considered the dif-
ferent problem of extracting operational (non ambiguous) role definitions from
protocol descriptions. Operational roles are expressed as multiset rewrite rules
in CAPSL [99], CASRUL [126], or sequential processes of the spi-calculus with
pattern-matching [49]. This extraction is also used for end-point projection
in [156, 155]. A pioneering work in this area is one by Carlsen [51] who has
proposed a translation of protocol narrations into CKT5 [36], a modal logic of
communication, knowledge and time.
Compiling narrations to roles has been extended beyond perfect encryption
primitives to algebraic theories in [55, 162]. An advantage of [162] is that it
supports implicit decryption which may lead to more efficient secrecy decision
procedures. We can note that, although these works admit very similar goals, all
their operational role computations are ad-hoc and lack of a uniform principle.
In particular they essentially re-implemented previously known techniques.
Our work Another motivation of this chapter is the existing amount of work
on the security analysis of cryptographic with various cryptographic primitives.
In these settings one considers operational models of the protocols given with-
out any justification. In particular there is no guarantee that the operational
model considered represents a prudent implementation of the protocol. A first
result of this chapter is the formalization of the notions of implementation and
prudent implementation in the sense that the receiver checks (and correlates)
the reachable parts of the received messages.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-96-320.jpg)
![6.2. ROLE-BASED PROTOCOL SPECIFICATIONS 97
As a consequence of these definitions we can relate the problems of comput-
ing a (prudent) implementation to classic decision problems, namely reachability
and static equivalence problems. In particular we describe how, given a deduc-
tion system, an algorithm solving the reachability problems for this deduction
system can be employed to compute an implementation, and how an algorithm
solving the refinement problem can be employed to compute a prudent imple-
mentation. This paves the way for using tools such as Yapa [29] to automatically
compile cryptographic protocols.
6.2 Role-based Protocol Specifications
First we show how we derive from a narration a plain role-based specification.
Then the specification will be refined in the following Sections.
6.2.1 Specification of messages and basic operations
We consider a slight variation of the basic notions from Chapter 4. We consider
an infinite set of free constants C and an infinite set of variables X . For each
signature F (i.e. a set of function symbols with arities), we denote by T (F)
(resp. T (F, X ) ) the set of terms over F ∪ C (resp. F ∪ C ∪ X ). The former is
called the set of ground terms over F, while the later is simply called the set of
terms over F. Variables are denoted by x, y, terms are denoted by s, t, u, v, and
finite sets of terms are written E, F, . . ., and decorations thereof, respectively.
In a signature F a constant is either a free constant in C or a function
symbol of arity 0 in F.
Deduction systems
Given its importance, let us recall the fundamental assumption underlying the
symbolic protocol analysis:
Fundamental assumption. Our work on the analysis of cryptographic proto-
cols rely on the assumption that all the agents operate on messages via a message
manipulation library.
Thus we have a signature F containing the function symbols employed to denote
the messages. In particular the functions of the library form a subset Fp of F.
Definition 28. (Deduction systems) A deduction system is defined by a triple
(E, F, Fp ) where E is an equational presentation on a signature F and Fp a
subset of public constructors in F.
Example 19. For instance the following deduction system models public key
cryptography:
({decp (encp (x, y), y −1 ) = x},
{decp ( , ), encp ( , ), −1 },
{decp ( , ), encp ( , )})](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-97-320.jpg)
![98CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
The equational theory is reduced here to a single equation that expresses that
one can decrypt a ciphertext when the inverse key is available.
Remark 2. The fact that we model the application of a function by equations
implies that, by transitivity of the equality, all the results f (t1 , . . . , tn ) of a
function f on a given sequence of arguments t1 , . . . , tn are equal. Thus we
can only model deterministic functions. This is not problematic for modelling
non-deterministic cryptographic primitives as it suffices to add an argument
representing the random part of the algorithm. However there are some cases
in which we want to model the ambiguity of a function. For these specific cases
we have introduced extended deduction systems [65, 57], but have chosen to not
present them in depth in this document in order to preserve its uniformity.
These extended deduction systems were introduced in [65] to model the non-
determinism in the handling of some messages by honest participants. The dif-
ference with standard deduction systems is that instead of deducing f (x1 σ, . . . , xn σ)
from any term x1 σ, . . . , xn σ when f is a public symbol, extended deductions
deduce a term (tσ)↓ from the terms (t1 σ)↓, . . . , (tn σ)↓. The only constraint is
that—omitting a technical detail for the sake of the clarity of exposition—we
impose that for every substitution σ every constant occurring in tσ must occur
in at least one of the (ti σ)↓.
Contexts. Let D be a deduction system. A D-context C[x1 , . . . , xn ] is a term
in which all symbols are public and such that its nullary symbols are either
public non-free constants or variables.
6.2.2 Role Specification
We present in this subsection how protocol narrations are transformed into sets
of roles. A role can be viewed as the projection of the protocol on a principal.
The core of a role is a strand which is a standard notion in cryptographic
protocol modeling [111].
A strand is a finite sequence of messages each with label (or polarity) ! or
?. Messages with label ! (resp. ?) are said to be “sent” (resp.“received”). A
strand is positive iff all its labels are !. Given a list of message l = m1 , . . . , mn
we write ?l (resp. !l) as a short-hand for ?m1 , . . . , ?mn , (resp. !m1 , . . . , !mn ).
Definition 29. A role specification is an expression A(l) : νn.(S) where A is a
name, l is a sequence of constants (called the role parameters), n is a sequence
of constants (called the nonces of the role), and S is a strand. Given a role r
we denote by nonces(r) the nonces n of r and strand(r) the strand S of r.
Example 20. For example, the initiator of the NSPK protocol is modeled, at
this point, with the role:
−1
νNa .(?Na , ?A, ?B, ?KA , ?KB , ?KA ,
!msg(B, encp ( A, Na , KB )),
?msg(B, encp ( Na , Nb , KA )),
!msg(B, encp (Nb , KB )))](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-98-320.jpg)

![100CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
!
Definition 30. Let r = νN.( ? Mi )1≤i≤n be a role specification, and let (R1 , . . . , Rk )
be the subsequence of the messages Mi labeled with ?. The input of r is denoted
input(r) and is the positive strand (!R1 , . . . , !Rk ).
In the next section we define a target for the compilation of role specifica-
tions. Then we compute constraints to be satisfied by sent and received mes-
sages. and by adding the constraints to the specification this one gets executable
in the safest way as possible w.r.t. to its initial specification.
6.3 Operational semantics for roles
In Section 6.2 we have defined roles and shown how they can be extracted from
protocol narrations. In this section we define what an implementation of a role
is and in Section 6.4 we will show how to compute such an implementation from
a protocol narration.
Intuitively an operational model for a role has to reflect the possible ma-
nipulations on messages performed by a program implementing the role. These
operations are specified here by a deduction system D = (E, F, S) where the set
of public functions S, a subset of the signature F, is defined by equations in the
equational theory E.
Active frames We introduce now the set of implementations of a role speci-
fication as active frames. An active frame extends the role notion by specifying
how a message to be sent is constructed from already known messages, and how
a received message is checked to ascertain its conformity w.r.t. already known
messages. The notation !vi (resp. ?vi ) refers to a message stored in variable vi
which is sent (resp. received).
Definition 31. Given a deduction system D with equational theory E, a D-
active frame is a sequence (Ti )1≤i≤k where
?
!vi with vi = Ci [v1 , . . . , vi−1 ] (send)
Ti = or
?vi with Si (v1 , . . . , vi ) (receive)
where Ci [v1 , . . . , vi−1 ] denotes a context over variables v1 , . . . , vi−1 and Si (v1 , . . . , vi )
denotes a E-unification system over variables v1 , . . . , vi . Each variable vi occur-
ing with polarity ? is an input variable of the active frame.
Example 21. The following is an active frame denoted φa that can be employed
to model the role A in the NSPK protocol:
(?vNa ?vA , ?vB , ?vKA , ?vKB , ?vK −1 ,
A
?
!vmsg1 with vmsg1 = msg(vB , encp ( vA , vNa , vKB )),
?vr with ∅
?
!vmsg2 with vmsg2 = msg(vB , encp (π2 (decp (vr , vK −1 )), vKB )))
A](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-100-320.jpg)
![6.3. OPERATIONAL SEMANTICS FOR ROLES 101
Compilation is the computation of an active frame from a role specification
such that, when receiving messages as intended by the role specification, the ac-
tive frame emits responses equal modulo the equational theory to the responses
issued in the role specification. More formally, we have the following:
Definition 32. Let D be a deduction system with equational theory E. Let
ϕ = (Ti )1≤i≤k be an active frame, where the Ti ’s are as in Definition 31, and
where the input variables are r1 , . . . , rn . Let s be a positive strand !M1 , . . . , !Mn .
Let σϕ,s be the substitution {ri → Mi } and S be the union of the E-unification
systems in ϕ. The evaluation of ϕ on s is denoted ϕ · s and is the strand
(m1 , . . . , mk ) where:
!Ci [m1 , . . . , mi−1 ] If vi has label ! in Ti
mi =
?vi σϕ,s If vi has label ? in Ti
We say that ϕ accepts s if Sσϕ,s is satisfiable.
To simplify notations, the application of a D-context C[x1 , . . . , xn ] on a
positive strand s = (!t1 , . . . , !tn ) of length n is denoted C · s and is the term
C[t1 , . . . , tn ].
Example 22. Let r be the role specification of role A in NSPK as given in
Example 20 and φA be the active frame of Example 21. Let M be the message
msg(B, encp ( Na , Nb , KA )). We have:
−1
input(r) = (!Na , !A, !B, !KA , !KB , !KA , !M )
and φA · input(r) is the strand:
−1
(?Na , ?A, ?B, ?KA , ?KB , ?KA ,
!msg(B, encp ( A, Na , KB )),
−1
?M, !msg(B, encp (π2 (decp (payload(M ), KA )), KB ))
Modulo the equational theory, this strand is equal to the strand:
−1
(?Na , ?A, ?B, ?KA , ?KB , ?KA ,
!msg(B, encp ( A, Na , KB )), ?M, !msg(B, encp (Nb , KB ))
It is not coincidental that in Example 22 the strands ϕ · input(r) and
strand(r) are equal as it means that within the active frame, the sent mes-
sages are composed from received ones in such a way that when receiving the
messages expected in the protocol narration, the role responds with the mes-
sages intended by the protocol narration. This fact gives us a criterion to define
what an implementations of a role is.
Definition 33. An active frame ϕ is an implementation of a role specification
r if ϕ accepts input(r) and ϕ · input(r) =E strand(r). If a role admits an
implementation we say this role is executable.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-101-320.jpg)
![102CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
Example φa defined above is a possible implementation of the initiator role
in NSPK. However this implementation does not check the conformity of the
messages with the intended patterns, e.g. it neither checks that vr is really an
encryption with the public key vKA of a pair, nor that the first argument of the
encrypted pair has the same value as the nonce vNa . In Section 6.4 we show not
only how to compute an active frame when the role specification is executable,
but also to ensure that all the possible checks are performed.
6.4 Compilation of role specifications
Usually the compilation of a specification is defined by a compilation algorithm.
An originality of this work is that we present the result of the compilation as
the solution to decision problems. This has the advantage of providing for free
a notion of prudent implementation as explained below.
6.4.1 Computation of a first implementation
Let us first present how to compute an implementation of a role specification in
which no check is performed, as given in the preceding example. To build such an
implementation we need to compute for every sent message m a context Cm that
evaluates to m when applied to the previously received ones. This reachability
problem is unsolvable in general. Hence we have to consider systems that admit
a reachability algorithm, formally defined below:
Definition 34. Given a deduction system D with equational theory E, a D-
reachability algorithm AD computes, given a positive strand s of length n and a
term t, a D-context AD (s, t) = C[x1 , . . . , xn ] such that C · s =E t iff there exists
such a context and ⊥ otherwise.
We will show that several interesting theories admit a reachability algorithm.
This algorithm can be employed as an oracle to compute the contexts in sent
messages and therefore to derive an implementation of a role specification r.
We thus have the following theorem.
Theorem 6.1. If there exists a D-reachability algorithm then it can be decided
whether a role specifications r is executable and, if so one can compute an im-
plementation of r.
!
Proof sketch. Let r = ( ? Mi )i∈{1,...,n} be an executable role specification. By
definition there exists an active frame ϕ that implements r, i.e. for each sent
message Mi , there exists a context Ci such that Ci [M1 , . . . , Mi−1 ] is equal to
Mi modulo the equational theory. Thus if there exists a D-reachability algo-
rithm AD , the result AD (M1 , . . . , Mi−1 ), Mi ) cannot be ⊥ by definition. As a
consequence, AD ((M1 , . . . , Mi−1 ), Mi ) is a context Ci [x1 , . . . , xn ]. Thus for all
index i such that Mi is sent we can compute a context Ci that, when applied on
previous messages, yields the message to send. We thus have an implementation
of the role specification.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-102-320.jpg)
![6.4. COMPILATION OF ROLE SPECIFICATIONS 103
6.4.2 Computation of a prudent implementation
We note that having an implementation of a role specification is of little use
w.r.t. the security analysis of a protocol. For example the active frame of
Example 21 is an implementation of the initiator of the NSPK protocol but it
will accept any message from the intruder without aborting.
Any of the algorithms proposed so far for the compilation of cryptographic
protocols would at least require that the role checks that the received message
contains the nonce sent at the first step. We now present an algorithm that
computes this kind of checks for arbitrary deduction system. It formalizes a
check as an equation between contexts over messages received so for, including
the initial knowledge. For example, and reusing the notations of Example 21 it
computes that upon reception of the message the initiator must, among other
tests, check the validity of the equation:
?
π1 (decp (payload(vr ), vK −1 )) = vNa
A
Let us first formalize what an acceptable message is by a refinement relation
on sequences of messages. We will say a strand s refines a strand s if any
observable equality of messages in strand s can be observed in s using the same
tests. To put it formally:
Definition 35. A positive strand s = (!M1 , . . . , !Mn ) refines a positive strand
s = (!M1 , . . . , !Mn ) if, for any pair of contexts (C1 [x1 , . . . , xn ], C2 [x1 , . . . , xn ])
one has C1 · s = C2 · s implies C1 · s = C2 · s.
For instance the strand s = (! encp (encp (a, k ), k), ! encp (a, k ), !k, !k , !a) re-
fines s = (! encp (encp (a, k ), k), ! encp (a, k ), !k, !k , !a) since all equalities that
can be checked on s can be checked on s. We can now define an implementation
φ to be prudent if every equality satisfied by the sequence of messages of the
role specification is satisfied by any sequence of messages accepted by φ.
Definition 36. Let r be a role specification and ϕ be an implementation of r.
We say that ϕ is prudent if any positive strand s accepted by ϕ is a refinement
of input(r).
Most deduction systems considered in the context of cryptographic protocols
analysis have the property that it is possible to compute, given a positive strand,
a finite set of context pairs that summarizes all possible equalities in the sense
of the next definition. Let us first introduce a notation: Given a positive strand
s we let Ps be the set of context pairs (C1 , C2 ) such that C1 · s = C2 · s.
Definition 37. A deduction system D has the finite basis property if for each
f
positive strand s one can compute a finite set Ps of pairs of D-contexts such
that, for each positive strand s :
f
Ps ⊆ Ps iff Ps ⊆ Ps](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-103-320.jpg)
![104CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
Let us now assume that a deduction system D has the finite basis property.
There thus exists an algorithm AD (s) that takes a positive strand s as input,
f
computes a finite set Ps of context pairs (C[x1 , . . . , xn ], C [x1 , . . . , xn ]) and re-
?
turns as a result the E-unification system Ss : {C[x1 , . . . , xn ] = C [x1 , . . . , xn ] | (C, C ) ∈
f
Ps }. For any positive strand s = (!m1 , . . . , !mn ) of length n, let σs be the sub-
stitution {xi → mi }1≤i≤n . By definition of Ss we have that σs |= Ss if and
only if s is a refinement of s. Given the preceding definition of AD (s, t), we
are now ready to present our algorithm for the compilation of role specifications
into active frames.
! !
Algorithm Let r be a role specification with strand(r) = ( ? M1 , . . . , ? Mn )
and let s = (!M1 , . . . , !Mn ). Let us introduce two notations to simplify the
writing of the algorithm, i.e. we write r(i) to denote the i-th labelled message
! i
? Mi in r, and s to denote the prefix (!M1 , . . . , !Mi ) of s. Compute, for 1 ≤ i ≤
n:
?
Ti = !vi with vi = AD (si−1 , Mi ) If r(i) =!Mi
?vi with AD (si ) If r(i) =?Mi
and return the active frame ϕr = (Ti )1≤i≤n . By construction we have the
following theorem.
Theorem 6.2. Let D be a deduction system such that D-ground reachability
is decidable and D has the finite basis property. Then for any executable role
specification r one can compute a prudent implementation ϕ.
6.5 Symbolic derivations
Active frames are sufficient to express the relationships between input and out-
put messages in a role implementation as well as to describe precisely which
messages are acceptable by a prudent implementation. However they do not
describe precisely the internal computations of an implementation. For example
the usage of contexts means that the output is computed only from the mes-
sage received and the initial knowledge, and thus that already computed values
have to be re-computed every time they are employed. Also, active frames do
not provide us with a communication model, i.e. a way to describe the mes-
sages exchanged during an execution of a protocol. We now introduce symbolic
derivations, a structure in which one can express both the communications and
the internal computations at the expense of heavier notations.
6.5.1 Definitions
Symbolic derivations. Given a deduction system (F, P, E), a role applies
public symbols in P to construct a response from its initial knowledge and from
messages received so far. Additionally, it may test equalities between messages
to check the well-formedness of a message. Hence the activity of a role can be
expressed by a fixed symbolic derivation:](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-104-320.jpg)
![6.5. SYMBOLIC DERIVATIONS 105
Definition 38. (Symbolic Derivations) A symbolic derivation for a deduction
system (F, P, E) is a tuple (V, S, K, In, Out) where V is a mapping from a finite
ordered set (Ind, <) to a set of variables Var(V), K is a set of ground terms (the
initial knowledge) In is a subset of Ind, Out is a multiset of elements of Ind
and S is a set of equations.
The set Ind represents internal states of the symbolic derivation. We impose
that any i ∈ Ind denotes a state of one of the following kind:
Deduction state: There exists a public symbol f ∈ P of arity n such that
?
S contains the equations V(i) = f (V(α1 ), . . . , V(αn )) with αj < i for
j ∈ {1, . . . , n} .
?
Re-use state: Otherwise, if there exists j < i with V(j) = V(i);
?
Memory state: Otherwise, if there exists t in K and an equation V(i) = t in
S;
Reception state: Otherwise, we must have i ∈ In;
Additionally, a state i is also an emission state if i ∈ Out.
A symbolic derivation is closed if it has no reception state. A substitution
σ satisfies a closed symbolic derivation if σ |=E S.
Remark 3. We believe that using symbolic derivations instead of more stan-
dard constraint systems permits one to simplify the proofs by having a more
homogeneous framework. There is however one drawback to their usage. While
most of the time it is convenient to have an identification between the order
of deduction of messages and their send/receive order, building in this identifi-
cation too strictly would prevent us from expressing simple problems. Re-use
states are employed to reorder the deduced messages to fit an order of sending
messages which can be different. For example consider an intruder that knows
(after reception) two messages a and b received in that order, and that he has to
send first b, then a. Since the states in a symbolic derivation have to be ordered,
we have to use at least one re-use state (for a) to be able to consider a sending
of a after the sending of b. We note that re-use states that are not employed
in a connection can be safely eliminated without changing the deductions, the
definition of the knowledge nor the tests in the unification system.
Remark 4. Symbolic derivations were originally defined in [65] w.r.t. extended
deduction systems. We refer the interested reader to [65] for the exact definition
in that case.
Example 23. Let us consider the cryptographic protocol for deduction system
DY where FD and PD have been extended by a free public symbol f :
A→B: encp (Na , pk(B))
B→A: encp (f (Na ), pk(A))
where
A knows A, B, pk(B), pk(A), sk(A)
B knows A, B, pk(A), pk(B), sk(B)](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-105-320.jpg)






![112CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
6.5.3 Decision problems
Satisfiability. Though it is expressed using different notations, the problem
of the existence of a secrecy attack on a protocol execution with a finite number
of messages is equivalent, in the setting of this chapter, to the satisfiability
problem below. It has been shown to be NP-complete in [190] for the standard
Dolev-Yao deduction system.
I-Satisfiability
Input: a HSD C
Output: Sat iff C = ∅
A variant of I-satisfiability is its restriction to set of inputs C which are
ground symbolic derivations, and that we call I-ground satisfiability.
I-Ground Satisfiability
Input: a ground HSD C
Output: Sat iff C = ∅
Equivalence. As a special case of a hyperproperty we are interested in the
equivalence of HSDs w.r.t. an active intruder.
Definition 43. Two HSDs Ch and Ch are symbolically equivalent iff Ch = Ch .
Thanks to Lemma 10.3, p. 200 we will see that when the states in the HSDs
are totally ordered this notion is the same as the one of symbolic equivalence
in [54].
I-Symbolic Equivalence
Input: Two honest I-symbolic derivations Ch and Ch
Output: Sat iff Ch = Ch .
Again it is possible to define a ground version of the I-symbolic equivalence
problem when the input consists in two ground symbolic derivations.
I-Symbolic Equivalence
Input: Two honest I-ground symbolic derivations Ch and Ch
Output: Sat iff Ch = Ch .
Remark. Let us remark that it makes sense to compare Ch and Ch only if
there exists a bijection between the in- and output states of these derivations
such that every closed connection between an ASD and Ch can be mapped, using
this bijection, to a closed connection between the same ASD and Ch . In order
to simplify notations we implicitly quantify over all connection functions such
that a composition is closed and satisfiable and consider the same connection
(modulo the bijection) with the two HSDs Ch and Ch .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-112-320.jpg)
![6.5. SYMBOLIC DERIVATIONS 113
6.5.4 Relation with static equivalence
The problem we consider is whether two cryptographic processes, represented by
HSDs in our setting, are observationally equivalent, in the sense that an attacker
cannot built a sequence of interactions that would produce different results when
applied to the two processes. Solving this problem has many applications. For
instance if the two processes only differ by a data value this shows that this data
is confidential. In [5] the observational equivalence problem for an attacker who
does not interact with the honest agents is reduced to the one of the static
equivalence between two sequences of messages.
In the broader setting in which an attacker interacts online with the honest
participants, [89] reduces the observational equivalence to trace equivalence for
a class of processes corresponding to honest symbolic derivations. Their trace
equivalence corresponds to symbolic equivalence in our setting.
Static equivalence.
Contexts. Let us first recall the notion of static equivalence between frames
as introduced in [5]. A frame is a substitution σ of finite support {x1 , . . . , xn }
hiding a finite sequence c of constants, which is denoted νc·σ. A public construc-
tor is a function symbol f of arity k such that, if the intruder knows t1 , . . . , tk
he also knows f (t1 , . . . , tk ). A public context M over the frame νc · σ is a term
whose variables are in the support of σ, whose constants are away from c and
whose other symbols are public constructors. Finally, equality is defined modulo
an equational theory E.
Constants. Without loss of generality, we can assume that all free constants
in a context M are away from those appearing in σ: the rationale for this as-
sumption is that if a free constant c0 is in σ but not in c we can always consider
the public contexts on the frame ν c, c0 · {x0 → c} ∪ σ which are the same—but
for the replacement of c by x0 —as those on the frame νc · σ. This motivates the
splitting of the set of free constants into two sets, C and Cnew , where C desig-
nates those free constants that can be used by honest users, and Cnew those that
can be used by an attacker. We emphasize here that, as in [5], the attacker can
manipulate terms containing constants in C. We have just ensured that these
constants have to be passed explicitely to the attacker through the substitution
σ. When considering symbolic derivations, this translates into imposing that
the knowledge of an ASD must contain only constants in Cnew .
Let us now recast the definition of static equivalence, as stated in [5], ac-
cording to these assumptions.
Definition 44. (Static equivalence) Two frames ϕ = νc · σ and ψ = ν c · τ
that have the same domain are statically equivalent if for any public contexts
M and N whose constants are away from c ∪ c one has M σ =E N σ iff one has
M τ =E N τ .
The definition of contexts corresponds to the notion of derivation in the
following sense: we define I to be the deduction system defined over a signature](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-113-320.jpg)
![114CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
F, modulo an equational theory E, with P equal to the set of public symbols. We
note that, given the possible deductions, the quantification is over all symbolic
derivations that takes in input terms in the frame and constants away from these
frames, and thus in Cnew . Static equivalence states that any couple (M, N ) of
contexts yields the same result in one frame iff it yields the same result in the
other frame. This suggests us to express static equivalence of frames in terms
of sets of solutions of symbolic derivations as follows.
First, to a substitution σ of finite support x1 , . . . , xn we associate the closed
symbolic derivation:
?
Cσ = (V, {V(i) = xi σ}i=1,...,n , Image(σ), ∅, {1, . . . , n})
with V of support {1, . . . , n}. To represent the construction of contexts by the
attacker, we consider symbolic derivations CI = (VI , SI , cI , InvarI , ∅), with
|InI | = n, and cI a finite subset of Cnew . The equality of two contexts M and
N over σ can then be translated as the satisfiability of the following composition
of symbolic derivations:
. . . . . . . . . . . . . . ..
. . . . . . . . . ..
. ........ . .
. . . .. .. M ....N Solution of Cσ
.. ..
. ?
c V (1)
O V (n)O V (iM ) V (iN ) S with: V (iM ) = V (iN )
?
V(1) V(n) {V(i) = xi σ}i∈{1,...,n} Cσ
Clearly, two frames νc·σ and νc·τ are statically equivalent, with the standard
definition, iff for any ASD C , C ◦ Cσ is closed and satisfiable iff C ◦ Cτ is closed
and satisfiable. In our notation this is translated into the equality Cσ = Cτ ,
and the problem of deciding whether two closed frames are in static equivalence
is the same problem as deciding whether two closed symbolic derivations are
symbolically equivalent.
Relation with ground symbolic equivalence. One could have expected to
have a definition of static equivalence in terms of ground symbolic equivalence.
But such a definition would have made the problem more difficult. Indeed, it has
only been shown in [4] that when there exists at least one free function symbol the
decidability of static equivalence implies the decidability of ground satisfiability.
This was actually taken into account in [11] where it is actually proven that
ground symbolic equivalence (in lieu of static equivalence) is modular.
Equational theories and equivalence
The original problem one is interested in is whether two cryptographic processes
are bisimilar for an external observer. In [5] this problem is reduced to the one
of the static equivalence between two sequences of ground messages. However
the cryptographic operations considered were total, which means e.g. that a
decryption applied on a message with a key always returns a message even](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-114-320.jpg)
![6.6. CONCLUSION 115
when the decryption key does not match the encryption key. As a result, the
observer is not aware of whether a cryptographic operation is successful. We
note that under these assumptions the frames:
ϕ = νa, k · {x1 → enc(a, k), x2 → k −1 }
ψ = νa, k , k · {x1 → enc(a, k ), x2 → k −1 }
are equivalent when assuming that an observer has no way to differentiate
a =E dec(x1 , x2 ) · ϕ and dec(enc(a, k ), k −1 ) = dec(x1 , x2 ) · ψ. This is e.g. the
case when no padding nor other security measure permits one to check that the
decryption has succeeded. But when one assumes that the cryptographic prim-
itives abstracted by the enc and dec symbols are such that dec(enc(a, k ), k −1 )
can be detected to be an incorrect decryption result (for example because it does
not have a correct padding), the two frames ϕ and ψ shall be distinguishables.
The choice between the two models shall be made on a per operation basis and
affects both the HSDs and the ASDs:
HSDs: In the second case, it makes sense to assume that there is no “decom-
position” symbol in the honest symbolic derivations considered (assuming
thereby that in a prudent implementation a raised exception would have
stopped the execution), while in the first case this distinction is irrelevant.
ASDs: In the second case, we have to ensure that the traces seen by the in-
truder are equivalent w.r.t. to equational rules applied on the contexts
constructed by the intruder, i.e. we have to ensure that the unification
system is normalized in the same way when composing an ASD with two
HSDs. Remembering that the equational theory models an arbitrary set
of functions with the possibility of recursive calls there is no generic way to
ensure that one can check that the same functions are successfully called.
However there is an important class of equational theories, namely those
for which some complete narrowing strategy terminates, for which one can
“symbolically” compute the possible function calls. This was employed in
the specific case of subterm equational theories in [75]. Technically, one
guessrd a set of narrowing steps on the unification system of an ASD be-
fore composing it with the HSDs. In the first case, one does not guess the
normalization steps before composing, and just relies on the satisfiability
of the unification system.
6.6 Conclusion
We have presented a formal model of cryptographic protocols which is amenable
to security analysis via the resolution of some decision problems. However this
model is defined for protocols described by narrations, which is not always
possible. Examples outside the scope of the translation presented include:
• protocols with loops, in which a sequence of actions can be repeated until
some criterion is satisfied;](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-115-320.jpg)
![116CHAPTER 6. SYMBOLIC MODELS FOR CRYPTOGRAPHIC PROTOCOLS
• protocols that do not fail silently when an unacceptable message is re-
ceived;
• protocols manipulating parameterized messages of unbounded size;
• group protocols, which are parameterized by the (unbounded number of)
members of a group, in which both the data and the actions can be pa-
rameterized;
• protocols in which the participants have access to sets of pieces of data,
e.g.:
– certificate revocation lists;
– databases, encoded by sets of messages;
– sets of nonces already used;
– timestamps;
– ...
This list is not exhaustive but most unabstracted cryptographic protocol already
falls into one or another category. The AVISPA and Avantssar tools can handle
partially some of these extensions, but we note that there is barely any published
article on these extensions except with very strong limitations. For example:
• T. Tr¨derung considered in [206] has proposed an extension to finite pro-
u
tocols in which the knowledge of the intruder is defined by a regular tree
language instead of being just a finite set of terms. It permits one to
partially encode the messages acceptable by Web Services, though the
limitations on the possible manipulations on the messages by the honest
participants are severely limited. An interesting extension of this work
would be to consider the case in which the keys are not atomic;
• R. K¨sters and T. Wilke [140] consider the case in which the honest par-
u
ticipants are modeled by regular transducers, i.e. finite state automata
rewriting the received the received message into a response. They proved
the decidability of the analysis for a class of regular transducers, and the
undecidability for several extensions of this class.
• N. Chridi, M. Turuani, and M. Rusinowitch [80] have considered a set-
ting in which the restrictions on the possible manipulations by the honest
participants are relaxed by using a severe tagging discipline;
• While these two works impose restrictions on the messages, I have con-
sidered in collaboration with D. Lugiez and M. Rusinowitch the case in
which honest participants can test the presence of a piece of data in a
database [66] by using positive subterm contraints. However in contrast
with the two previously mentionned works the setting adopted does not
permit one to express constraints imposing e.g. that a message contains
a sequence of messages of a particular type.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-116-320.jpg)


![Chapter 7
Proposition for WS
Modeling
We present in this chapter a framework in which one can ex-
press the access control policy of a service as well as the tran-
sition rules dealing with both the access control policy on a
workflow and its dynamic evolution. Each service is protected
by a trust negotiation policy that controls the accessibility of
the credentials used in the decision making in other services.
Unlike most of the access control policies which are uniquely
based on roles, we chose an attribute based framework leading
to more flexibility in the characterization of users. The strength
of this framework is its ability to control and check the access
control aspect of the services and its dynamic evolution based
on an exchange of credentials. We provide a unified framework
for reasoning on access control policies, trust negotiation and
workflows.
7.1 Introduction
There is an increasingly widespread acceptance of Service-Oriented Architecture
as a paradigm for integrating software applications within and across organi-
zational boundaries. In this paradigm, independently developed and operated
applications and resources are exposed as (Web) services. These services com-
municate one with another by passing messages over HTTP, SOAP, etc. A
fundamental advantage of this paradigm is the possibility to orchestrate exist-
ing services in order to create new business services adapted to a given task.
Several languages (WS-CDL [131], WSBPEL [128], BPMN [213],. . . ) have been
proposed to describe the workflow of an orchestrating service. These languages
can be given an operational semantics in terms of (extension of) π-calculus [149]
or Petri nets [122].
119](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-119-320.jpg)
![120 CHAPTER 7. PROPOSITION FOR WS MODELING
For business, security and legal reasons, it is necessary to control within a
workflow and on the workflow interface in which contexts an action can be exe-
cuted. This implies that, together with the workflow defining the orchestrating
service one has to provide an application-level security policy describing the
role, separation of duty and other constraints to be enforced in the workflow.
In order to foster agility (i.e. to specify the process so that it can be employed
in a variety of environment) one usually adds a trust negotiation layer so that
principals can get the chance to prove that they are legitimate users of the
service.
Given the skills required to implement these aspects, they are usually sep-
arated into a security token server, an XACML firewall, a Business Process
management system, plus additional ones for aspects abstracted in this paper.
We have chosen to describe services with logical entities that gather all the
aspects pertaining to one application or resource. The main originality of this
work is the interplay between workflow execution and access control which is
permitted by this unified framework. It permits us to express naturally the
constraints that are encountered when dealing with real-life business processes.
Related works. There exists already some works aiming at adding an access
control aspect to workflows. In [35, 175] the access control is specified with
roles that can execute activities, users that have attributes allowing them to
enter roles, and ordering on activities. We believe that RBAC-WS-BPEL lan-
guage is significantly less expressive than our proposal. In particular it does
not provide for dynamic separation of duty constraints, or other complex con-
straints based on the documents exchanged and the environment of execution.
In [133] is proposed a framework in which even messages are interpreted as
mobile processes, and in which processes communicate one with another to ex-
change credentials. The trust negotiation rules and their evaluation is similar
to what we propose, but the workflow description is absent and thus we believe
it to be much harder to express fine access control policies that depend on the
execution so far of a processus. Moreover the overall architecture is completely
different. In [121, 30, 107] the workflow is embedded within the access control
system, i.e. the possible evolutions of a process are embedded in the access
control rules. Another point is that there is no notion of local state, which is
replaced by the proof of reachability of a state . This approach implies that one
does not follow exactly how many times a given task is executed.
In Sect. 7.2 we give an informal description of the model. We present the
access control rules and the workflow in Sect. 7.3. Section 7.4 gives the semantics
of access control rules and Section 7.5 presents the operational semantics of the
workflow.
7.2 The model
Our aim is to develop a language that is capable of managing access control
policies and state evolution in a distributed environment. In this section we](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-120-320.jpg)
![7.2. THE MODEL 121
present the structure of our framework by defining the different constituents of
the model.
7.2.1 Presentation of the car registration process (CRP)
Before giving a formal description of the model, we present a concrete case study
[202] to illustrate the use of this dynamic framework. Mike is a citizen and wants
to register his newly purchased car. To do so he sends a completed registra-
tion form to the car registration office along with all the necessary documents.
The car registration office acts as a portal between the employees that study
the document form and make a decision on one hand, and the central reposi-
tory where the forms are to be stored on the other hand. The car registration
office allows employees to access and store documents in its local repository.
When a request form is studied and a decision is made, the document has to be
stored in the central repository and the citizen has to be notified of the decision
through the car registration office. Employees can access documents in the cen-
tral repository and they can store documents in the central repository only if
they have a certificate form their boss. The Registration office central authority
provides the needed certificates for both the employees and the head of the car
registration office. Employees can access the documents in the local repository,
make comments and store them back in the local repository at all times. Once
a decision is taken, the document shall be stored in the central repository and
the citizen is to be notified.
7.2.2 On the encoding of CRP into our framework
An overall view leads us to define three distinct concepts upon which the model
is built.
An entity is an abstract service formed of a set of access control rules, a set
of negotiation rules, a repository containing certificates and documents and a
workflow that orchestrates the state evolution. In addition, an entity possesses
a set of local identifiers that can be used in any rule within the entity. The
access control policy of the entity is state-based and attribute-based, i.e. the
decisions are taken by examining its local state and provided certificates. In the
above example we can distinguish between four different entities, namely the car
registration office(CRO), the central repository(CR), the Central authority(CA)
and the employee(Empl), each having its own access control policy and set of
permitted actions. For example, the access control policy of (CR) states that an
employee can store a document if a certificate from his/her boss certifies that
he/she can store document in the central repository, whereas in the (CRO) a
certificate stating that the user is an employee is enough to allow the user to
store a document in the local repository.
A local state associates values to the local identifiers and to the workflow
variables. The local state of an entity evolves depending on the actions per-](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-121-320.jpg)



![7.3. SYNTAX 125
and thus a doubly exponential number of terms. Given a set C of constants we
denote H(C) the set of ground terms built over these constants. We note that
this set is at most of doubly exponential size w.r.t. the number of constants.
Messages and certificate messages. Messages are employed to exchange
ground terms between entities. We distinguish two kinds of messages:
• A certificate message CM is a triple cert(C, t1 , t2 ) where C is a ground
certificate and t1 , t2 are ground terms denoting the sender and receiver
respectively;
• A message has the form msg(L, t1 , t2 , τ ) where L is a ground list, and
t1 , t2 are atomic values denoting the sender and receiver respectively, and
τ ∈ Act;
7.3.2 Access control rules
The entity has two sets of rules, one is responsible for the protection of the
certificate exchange and the other manages the permissions for the tasks that
can be executed within the entity. Although both are represented by predicate
logic rules, their purpose and semantics is different. We shall first present the
rules that govern the trust negotiation. We then define the access control rules
that govern the dynamic evolution of the entities. The rule evaluation semantics
will be presented in Sect.7.4.
Trust negotiation.
In a distributed environment entities need to exchange information in order
to validate the decision of another entity via the use of certificates containing
information—which may be sensitive—about the users or resources that act on
its behalf in other entities. We model this exchange via a trust negotiation
mechanism where each entity can set its own trust policy for the disclosure of
certificates to the entities. The trust negotiation is triggered by a request that
usually emanates either during an access control evaluation rule or during a
negotiation session. These rules have the form:
put(C, t) ← body
where put(C, t) allows the disclosure of certificate (i.e. a value of type certificate)
C to an entity t (a value of type atomic) whenever the conditions in the body
of the rule are satisfied.
Access control policy.
When writing a Business Process, one usually differentiates between atomic
actions, tasks [117] which are defined by partial orderings on atomic actions,
and business roles which are entities to which a set of tasks is assigned. We](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-125-320.jpg)




![130 CHAPTER 7. PROPOSITION FOR WS MODELING
Global states. We use multiset rewriting (see [52] for a presentation and for
its relation with π-calculus) to specify global states of the system under analysis.
A state is a couple of:
• A multiset M that represents messages that have been sent and not yet
received. This multiset permits us to consider asynchronous communica-
tions between entities.
• A multiset E of entities that represents the different service instances (with
their multiplicity) at the current point of execution.
We assume that in an initial state, the multiset M of messages is empty. We
present the transition relation on the states in the next two sections. In Sect. 7.4
we present the semantics for trust negotiation, on which we rely in Sect. 7.5 to
define one-step transitions.
7.3.5 Example
We extract from our running example the following workflow:
store(X, Y ) = modif y(status, Y, ⊥); add(Y, DocList)
W =
νU, Doc; recv(Doc, U, store op); store(U, Doc)
In the entity (i, ρi , {DocList → ∅}, W ). The first executable action is νU, Doc
that creates new variables, and results in the local state:
(i, ρi , {DocList → ∅, U → ⊥, Doc → ⊥},
recv(Doc, U, store op); store(U, Doc))
The action recv(Doc, U, store op) is now executable. Assuming a matching
message msg(doc0 , u, i, store op) is waiting to be received, this action can be
executed, and will result in the entity state:
(i, ρi , {DocList → ∅, U → u0 , Doc → doc0 },
store(U, Doc))
This action is then replaced by the definition of store(X, Y ) by substituting X
with U and Y with Doc. This replacement is permitted if P ermit(store doc(u0 , doc0 ))
is derivable from the access control policy, and will result in the entity state:
(i, ρi , {DocList → ∅, U → u0 , Doc → doc0 },
modif y(status, Doc, ⊥); add(Doc, DocList))
In Sect. 7.4 and 7.5 we formalize the transition rules on global states, and
thereby the operational semantics for processes and entities.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-130-320.jpg)
![7.4. SEMANTICS FOR ACCESS CONTROL 131
7.4 Semantics for access control
7.4.1 Application of substitution in an entity
We distinguish between three types of values, namely terms instantiated by
constant values, certificates, documents, sets and lists. We assume that variables
are of one of these types. We define in this substitution the application of a
substitution σ in the context of an entity Ei = (i, ρi , σi , Wi ). Assuming that all
substitutions are well-typed, we define, when applying a substitution σ in ρi :
xσi , x ∈ dom(σi ) and xσi = ⊥
- For a variable x ∈ V [[x]]i =
σ xσ, otherwise.
- For a constant c ∈ C [[c]]i = c
σ
- For self [[self ]]i = i the identity name of an entity E.
σ
[[X.a]]i = v if [[a]]i = att and (att, v) ∈ [[X]]i .
σ σ σ
- For a certificate or document X:
[[X.a]]i = ⊥ if [[a]]i = att and (att, v) ∈ [[X]]i for all v
σ σ σ
- For a task τ ∈ Act, [[τ (v1 , . . . vn )]]i = τ ([[v1 ]]i . . . [[vn ]]i )
σ σ σ
7.4.2 Predicate evaluation
We start by giving meaning to the predicates evaluation in order to define later
rule evaluation for rules of the form h ← body. We use the notation |=i to express
that the predicate evaluation is local to the rules in entity E of identifier i but
takes into account the global exchange of certificates. As such, let α0 be the set
of communicated certificates, and let σ be a ground well-typed substitution.
Recall that M represent the multiset of messages sent but not yet received
and E represent the multiset of entities. The expression S + s represents the
fact that there exists an element s in the multiset S. Subsequently, the notation
S denotes that the element s was omitted from S.
- M, E + (i, ρi , σi , Wi ), α0 , σ |=i
- M, E + (i, ρi , σi , Wi ), α0 , σ |=i get(v, t) if ([[t]]i , [[v]]i , i) ∈ α0 .
σ σ
- M, E+(i, ρi , σi , Wi ), α0 , σ |=i has(v, S) if there exists a set [[S]]i in range(σi )
σ
such that [[v]]i ∈ [[S]]i
σ σ
- M, E + (i, ρi , σi , Wi ), α0 , σ |=i x = y(x = y) if [[x]]i = [[y]]i ([[x]]i = [[y]]i )
σ σ σ σ
7.4.3 Rule evaluation
Trust negotiation.
Trust negotiation is a global mechanism and its result is evaluated in the global
state. A certificate c can be sent by i to the requester r, if in entity Ei =
(i, ρi , σi , Wi )
M, E + (i, ρi , σi , Wi ), α0 |=i put(c, r)](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-131-320.jpg)
![132 CHAPTER 7. PROPOSITION FOR WS MODELING
is true, that is if there exists a rule h ← body in ρi and a ground well-typed
substitution σ such that:
[[h]]i = put(c, r)
σ
M, E + (i, ρi , σi , Wi ), α0 |=i body
A trust negotiation for a certificate (c, i, r) is a success, where i is the sender
and r the receiver, if the certificate is deducible from the previous sequence of
already communicated certificates. Namely, given the current global state and
a possibly empty initial sequence of certificates α0 ,
M, E, α0 |= (c, i, r) iff M, E + (i, ρi , σi , Wi ), α0 |=i put(c, r)
A trust negotiation for a certificate sequence α is a success if for every certificate
message in α we can check that the certificate is deducible from the previous
sequence of already communicated certificates. Namely, given a global state
with a set of already sent messages α0 :
M, E + (i, ρi , σi , Wi ), α0 |= (c, i, r)
M, E, α0 |= (c, i, r) · α iff
M, E + (i, ρi , σi , Wi ), α0 · (c, i, r) |= α
When the sequence of certificates is empty, we set that M, E, α |= λ.
Access control rules.
We now present the access control rules evaluation. We start by the semantics
of the local evaluation, namely given an entity Ei = (i, ρi , σi , Wi ) ∈ E we say
that:
M, E + (i, ρi , σi , Wi ) |=i P ermit(τ (v1 , . . . , vn )
is true if there exists a ground sequence of certificates α and a rule h ← body ∈ ρi
such that
[[h]]i = P ermit(τ (v1 , . . . , vn ))
σ
M, E + (i, ρi , σi , Wi ), α |=i body
M, E |= α
7.5 Workflow operational semantics
We present below the reduction rules for atomic actions that are responsible
for the state evolution of the workflow. We shall first present the notion of
evaluation context, is a context C[−] whose hole is under an iteration, an input
or an output. We shall use this notion to restrict the process substitution
to one given process outside the scope of parallelism. We assume that new
variables can only be created by ν. In what follows we give the semantics for
the transition relations. Recall that the local state of the entity is defined by
the tuple (i, σi , ρ, W ).](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-132-320.jpg)
![7.5. WORKFLOW OPERATIONAL SEMANTICS 133
Variable creation
M, E + (i, σi , ρ, C[νxi , . . . , xl .P ])
↓ {x1 , . . . , xn } ∩ dom(σi ) = ∅
M, E + (i, σi , ρ, C[P ])
⊥, x ∈ {xi , . . . , xl };
with σi = x →
xσi , otherwise.
Task invokation
If there exists a sequence of certificate messages α such that M, E+(i, σi , ρ, W ), α |=i
P ermit([[τ (x1 , . . . xn )]]i )
σ
M, E + (i, σi , ρ, C[τ (x1 , . . . , xn ).P ])
↓ [ (x1 ,...,xn )σ ı]
[τ ]
M, E + (i, σi , ρ, C[pi (x1 , . . . xn ).P ])
where τ (x1 , . . . , xn ) = pi (x1 , . . . xn ) is defined in the workflow and: σi = x →
[[x]]i for x ∈ dom(σi )
σ
Send action
M, E + (i, σi , ρ, C[snd(v1 · . . . · vn , vr , τ ).P ])
↓ snd(v1 ·...·vn ,vr ,τ )σi
M + msg(v1 · . . . · vn , i, vr , τ )σi , E + (i, σi , ρ, C[P ])
Receive action
M + msg(t1 · . . . · tn , s, i, τ ), E + (i, σi , ρ, C[rcv(v1 · . . . , ·vn , vs , τ ).P ])
↓ rcv(t1 ·...·tn ,s,τ )
vi σ = ti , vs σ = s
M, E + (i, nextrcv (σi , σ), ρ, C[P ])
xσ, x ∈ {v1 · . . . , ·vn , vs };
with nextrecv (σi , σ) = x →
xσi , otherwise.
Add action
M, E + (i, σi , ρ, C[add(v, S).P ])
↓ add(vσi ,Sσi )
M, E + (i, σi , ρ, C[P ])
{[[v]]i } ∪ [[S]]i , x = S;
σ σ
with σi = x →
xσi , otherwise.
Remove action
M, E + (i, σi , ρ, C[rmv(v, S).P ])
↓ rmv(vσi ,Sσi )
M, E + (i, σi , ρ, C[P ])
Sσi {vσi }, x = S;
with σi = x →
xσi , otherwise.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-133-320.jpg)
![134 CHAPTER 7. PROPOSITION FOR WS MODELING
Modify action
M, E + (i, σi , ρ, C[mdf y(a, X, v).P ])
↓ mdf y(a,Xσi ,vσi )
Xσi .a = ⊥
M, E + (i, σi , ρ, C[P ])
Xσi ∪ {(a, vσi )}, x = X;
with σi = x →
xσi , otherwise.
Modify action
M, E + (i, σi , ρ, C[mdf y(a, X, v).P ]), σ
↓ mdf y(a,Xσi ,vσi )
(a, t) ∈ Xσi ,
t = vσi
M, E + (i, σi , ρ, C[P ])
Xσi {(a, t)} ∪ {(a, vσi )}, x = X;
with σi = x →
xσi , otherwise.
7.6 Conclusion
We have defined a logical framework to express the dynamic evolution of an
entity by defining a set of access control rules taking into account trust negoti-
ation with other entities in the environment on one hand and a workflow that
describes the state evolution on the other hand. The workflow is capable of
processing the execution of permitted tasks within the entity and the commu-
nication of messages with other entities. The communication is asynchronous,
however the communication of the messages synchronize the execution of the
different workflows by being guards on the execution of tasks. This framework
can be seen as a generic model that mimics the work of a business process.
Each entity represents the flow of a given service and the business process is
represented by the global flow. Future work is in the direction of formalizing
the notion of message communication. We also plan to explore the expressivity
of this framework by examining the notions of delegation, separation of duties,
and other features of access control. Also we find that some complexity analysis
are necessary to study the efficiency of the framework.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-134-320.jpg)


![Chapter 8
Cryptographic Protocols
Refutation
The work on the refutation of cryptographic protocols in the
case of a finite number of messages exchanged by honest partic-
ipants is at the core of my research. I consider in this chapter the
classical part dealing with the refutation of trace-based security
properties.
8.1 Locality
One could argue that all deduction systems for which it was proven that the
satisfiability of a symbolic derivation is decidable have in common that the
deduction system is local, i.e. is such that in the case of ground satisfiability it
suffices to consider the ASDs in which only ground term appearing in the HSD
need to be deduced.
We first define locality using the notations related to symbolic derivations.
Then we present the definition of oracle deduction systems as given in [68]
and later re-used in [69] and other papers. We give a short summary of the
decidability proof in [68], with an emphasis on the common points with [69] and
other works. Finally we discuss the actual importance of this notion.
8.1.1 Locality
The notion of locality was first defined in the first-order logic context by [118],
and later refined for first-order entailment problems by [26, 25]. Before proceed-
ing further let us recall this notion as it was originally introduced by [118] in
the language of symbolic derivations.
Definition 45. (Locality) A deduction system D is local if for every ground
symbolic derivation Ch with Ch = ∅ there exists (C, ϕ) ∈ Ch with Sub(TrCh ◦ϕ C (C)) ⊆
Sub(TrCh ◦ϕ C (Ch )).
137](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-137-320.jpg)
![138 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
We note in the above definition that since Ch is ground there exists a ground
substitution σ such that for every C ∈ Ch we have σ = TrCh ◦ϕ C (Ch ). The
definition thus implies that there exists a finite set of terms T = Sub(σ) such
that Ch = ∅ implies that this set contains an ASD in which every state is
instantiated by a term in T . This approach, i.e. locality w.r.t. a finite set of
terms is employed in [34] to provide new decision results for ground satisfiability
problems. In parallel to that work and in collaboration with M. Kourjieh [134]
I have also considered the notion of locality w.r.t. a well-founded simplification
ordering, and proved that that notion implied the notion of locality as defined
in [34]. Although our notion of locality is subsumed by the one of Bernat and
Comon-Lundh we believe it may be of practical interest given that it is often
simpler to provide a well-founded simplification ordering on ground terms than
to explicitly compute the finite set as in [34].
8.1.2 Oracle Deduction Systems
Let us now present an example usage of the notion of locality by giving the
definition of oracle deduction systems given in [68]. At that time the analysis
of cryptographic protocols was performed in the perfect cryptography model
defined by Dolev and Yao in [106]. However we wanted to extend this model
with additional deductions for two reasons:
• First, and in collaboration with Laurent Vigneron, we had provided earlier
a notion of oracle rules [77, 79] that turn the parallel executions of a
protocol into additional deduction rules for the intruder. We had a doubly-
exponential time complexity of the analysis, but suspected that a singly-
exponential algorithm existed;
• Second, and in the context of the AVISS project, we had started to work
on cryptographic protocols that relied on non-perfect cryptography by
exploiting the properties of the exclusive-or or of the modular exponenti-
ation.
In collaboration with Ralf K¨sters we have searched under which conditions it
u
is possible to extend the deduction system modelling the attacker defined by
Dolev and Yao to account for the oracle rules and the imperfect primitives.
First let us describe the Dolev-Yao deduction system, and then we present the
definition we ended up with.
Dolev-Yao deduction system. The signature FDY contains 3 symbols of
arity 2, namely , , encs ( , ), and decs ( , ) describing respectively the con-
catenation of two messages, the encryption of a message (its first argument) by
a symmetric encryption algorithm where the key is the second message and the
converse operation of decryption. It also contains two projection symbols of
arity 1, namely π1 ( ), π2 ( ).](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-138-320.jpg)
![8.1. LOCALITY 139
All these symbols can be employed by any agent, and we have thus the
following deduction rules:
Concatenation
Encryption
x, y x, y x, y encs (x, y)
p
FD =
x
π1 (x) x, y decs (x, y)
x π2 (x)
The equational theory ED contains the following relations:
Concatenation Encryption
ED = π1 ( x, y ) = x decs (encs (x, y), y) = x
π2 ( x, y ) = y
p
The deduction system DY = (FD , FD , ED ) describes the classical Dolev-Yao
equational model with pairing and symmetric encryption.
Oracle deduction systems. In [68] we have considered the extension of
the Dolev-Yao deduction system DY with another deduction system Dg =
p p p
(Fg , Fg , Eg ) with Fg ∩ FDY = ∅. We say that Dg is a guessing deduction
system if the following condition holds:
For every closed DY symbolic derivation C = (V, S, K, In, Out)
with σ = TrC ()C a substitution in normal form, and for every
?
deduction step i in Ind, with the corresponding equation V(i) =
f (V(i1 ), . . . , V(ik )) in S, we say that i is a:
• regular composition step if V(i)σ = f (V(i1 )σ, . . . , V(ik )σ) (the
equality here is in the empty theory) and f ∈ PD ;
• regular decomposition step if f ∈ PD but V(i)σ = f (V(i1 )σ, . . . , V(ik )σ);
• guess decomposition step if V (i)σ is a strict subterm of one of
the V(ij )σ for 1 ≤ j ≤ k;
• guess composition step if every strict subterm of V (i)σ is a
subterm of one of the V(ij )σ for 1 ≤ j ≤ k.
An index i is a composition (resp. decomposition) step if it is either a regular
composition (resp. regular decomposition) or guess composition (resp. decom-
position step). We finally say that the result of step ij is decomposed at step
?
i ij if V(i) = f (i1 , . . . , ik ) is in S and V(i)σ is a strict subterm of V(ij )σ 1
Let be a well-founded simplification ordering on terms.
Definition 46. (Oracle deduction systems) Let D be the union of DY with a
guessing deduction system Dg . We say that Dg is an oracle deduction system if:
1. D is local;
1 see [68] for the exact definition according to which a, b is not decomposed at step i if
?
V(i) = decs (V(j), V(k)) and σ maps V(j) to encs (a, a, b ) and V(k) to a, b .](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-139-320.jpg)


![142 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
can argue that the second point of the definition of oracle deduction systems is
another locality condition or, more accurately, a saturation condition.
However we believe that such an argumentation is weak because a) the sub-
term relation employed is not the standard one, and b) the deduction system
has been altered.
Changes in the subterm relation. When excluding the prefix oracle rules
of [68] all other examples of oracle deduction systems rely on a re-definition of
the subterm relation. The definition of subterms employed in [68, 69] is based
on the factors w.r.t. the equational theory of Dg . In [68] this equational theory
is the one of the bitwise exclusive-or ⊕ with equations:
x⊕y = y⊕x x ⊕ (y ⊕ z) = (x ⊕ y) ⊕ z
x⊕x = 0 x⊕0 = x
whereas in [69] the equational theory was the union of the one for multiplicative
abelian groups:
x×y = y×x x × (y × z) = (x × y) × z
x × inv(x) = 1 x×1 = x
and a simplified, decidable [130] set of equations modelling the modular expo-
nentiation:
exp(x, 1) = x
exp(exp(x, y), z) = exp(x, y × z)
In both cases the terms whose root symbol belongs to the Dolev-Yao signature
are free w.r.t. the considered equational theory.
Changes in the deduction system. Given that [68] defines a bitwise exclusive-
or operation one would expect its deduction system to contain ⊕ and 0 as public
symbols, and no other. However using this deduction system would not yield
a local deduction system. For example if the attacker must deduce the term
a1 ⊕ an after receiving the terms a1 ⊕ a2 , a2 ⊕ a3 , . . . , an−1 ⊕ an he has to com-
pute all the intermediate sums, none of which are subterms of either a1 ⊕ an
nor of any of the ai ⊕ ai+1 for 1 ≤ i ≤ n − 1.
The trick employed in [68] consists in computing the transitive closure of
the deduction system Dg . That is instead of denoted possible deductions with a
public symbol we employ terms, and the equation associated to a step i in which
?
a deduction using the term t is performed is V(i) = tθ, where θ is a substitution
mapping the variables of t to {V(1), . . . , V(i − 1)}. The computation of the
transitive closure in practice implies that Dg contains an infinite number of
public terms, which in turn implies that the second point of oracle deduction
systems definition is not trivially met.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-142-320.jpg)
![8.2. COMBINATION OF DECISION PROCEDURES 143
Conclusion. The two changes, on the subterm relation and on the deduction
sytem, that were performed to obtain decidability results are generic, and can
be defined for every deduction system. In the next section we review how they
can be applied to obtain combination algorithms for the modular resolution of
D-satisfiability problems.
8.2 Combination of decision procedures
8.2.1 Presentation of the problem
As noted in the preceding section, the main ingredients of the extension of the
Dolev-Yao deduction system are:
1. the definition of a subterm relation based on the notion of factors;
2. the computation of a transitive closure of the deduction system;
Besides these ingredients we needed the decidability of the ground satisfiability
problems and a way (the last point of the definition of oracle rules) to reduce
satisfiability problems to ground satisfiability ones.
A natural question then arises:
assuming the Dolev-Yao deduction system DY is extended with
a deduction system Dg and that Dg satisfiability problems are decid-
able, are (Dg ∪ DY)-satisfiability problems decidable ?
Actually one could generalize, and wonder whether the Dolev-Yao deduction
system plays a special rˆle. This leads to the following problem:
o
Symmetric combination problem: Assume that D1 and D2
are two deduction systems such that D1 -satisfiability problems and
D2 -satisfiability problems are decidable. Are (D1 ∪ D2 ) satisfiability
problems decidable ?
A second way to generalize is to investigate the conditions under which one can
extend an arbitrary (instead of only the Dolev-Yao one) with another deduction
system:
Asymmetric combination problem: Assume that D1 and
D2 are two deduction systems such that D1 -satisfiability problems
are decidable. Are (D1 ∪ D2 ) satisfiability problems decidable ?
I have considered these two problems in collaboration with M. Rusinowitch.
We have given a solution to the symmetric combination problem in [70, 76],
and a solution to the asymmetric combination problem in [71, 72]. We briefly
present these results in the rest of this section.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-143-320.jpg)
![144 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
8.2.2 Symmetric Combination problem
Background on the combination of equational theories
Background. There has been substantial works on the area of the combi-
nation of decision procedures for problems related to equational theories. But
before describing the ones relevant to our work, let us first introduce some no-
tations and definitions. We say that two equational theories are disjoint if they
do not share any function symbol. A theory E is consistent if it has a model
with more than one symbol or, equivalently, we do not have a =E b for two
free constants a and b. Let E1 and E2 be two disjoint equational theories. We
say that a term t is a pure E1 -term (resp. E2 -term) if it is built from function
symbols in the signature of E1 and variables. A term t is alien to E1 if its root
symbol is a function symbol in E2 or a free constant. By definition of syntac-
tic unification it is clear that terms alien to E1 are free (see the definition in
Section 4.7.3, p. 71).
A result by Tid`n [204] states that the combination of two disjoint consistent
e
equational theories E1 and E2 is a conservative extension of both E1 and E2 , i.e.
for terms s, t built using the functional symbols of the signature of E1 we have
s =E1 t if, and only if, s =E1 ∪E2 t. This theorem justifies the purification
procedure during which a (E1 ∪ E2 )-unification system S is transformed into the
union of two unification systems S1 and S2 in which Si is a Ei -unification system,
for i ∈ {1, 2}. This procedure replaces in t each factor s of a term t by a variable
?
xs and adds to S an equation xs =E1 ∪E2 s. It is clear that every unifier of S can
be extended into a unifier of S1 ∪ S2 . Conversely, the equations added impose
that all the variables replacing a given term s have to be equal to the instance
s, which permits one to reconstruct a unifier of S from every unifier of S1 ∪ S2 .
Given that E1 ∪ E2 is a conservative extension of each of the Ei one could
expect that once S is split into S1 ∪ S2 it would suffice to compute unifiers
modulo Ei of Si , for i ∈ {1, 2}, in order to compute unifiers of S. This logical
step is however not sound for two reasons:
symbol clash: it may happen that the same variable x ∈ Var(S1 ) ∩ Var(S2 ) is
instantiated differently by the unifiers σi of Si modulo Ei , for i ∈ {1, 2};
occur-check: it may happen that it is not possible to reconstruct a global
solution from σ1 and σ2 because of a cycle. As a degenerate case consider
? ?
the two unification systems {f (x) = y} and {g(y) = x} in the empty
?
theory. Each has a solution but the union unification system {f (x) =
?
y, g(y) = x} does not have one.
Deciding to compute a E1 (resp. E2 ) unifier σ1 (resp. σ2 ) of S1 ∪ S2 would be
sound but incomplete, as each unifier would be computed assuming that the
alien equations have to be true in the empty equational theory. For example
when combining the equational theory of the bitwise exclusive-or ⊕ with another
?
theory, every equation x ⊕ x = 0 would appear as unsatisfiable (because of a
root symbol clash) in the other equational theory.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-144-320.jpg)
![8.2. COMBINATION OF DECISION PROCEDURES 145
Combining unification or unifiability decision procedures for the disjoint
union of equational theories means finding a way to compute a unifier of S1 ∪ S2
modulo E1 ∪ E2 from Ei -unifiers of Si , for i ∈ {1, 2}.
Difficulty of the combination of decision procedures. First, and in order
to avoid symbol clashes, [191] introduces two non-deterministic steps:
• first one non-deterministically identify the variables that denote terms
equal modulo E1 ∪ E2 once the (putative) unifier is applied;
• then each variable x is assigned to one of the theory, say E1 . When re-
solving S2 modulo E2 this variable will be considered as a free constant.
These steps are justified as follows. Assuming the existence of a unifier σ in
normal form of S1 ∪ S2 the algorithm choose theory Ei for x if, and only if, the
root symbol of xσ belongs to the functional signature of E1 . Whenever x occurs
in S1 ∪ S2 as a variable of a E2 -pure term t, we note that xσ is a subterm of tσ
free in E2 and in normal form. Also all the factors of t are in normal form.
Thus when considering only the unification system S2 we can build from
σ a pure unifier in E2 by applying Lemma 4.22, p. 72 to replace xσ in the
terms of S2 σ with a free constant cxσ . The second step consists in applying this
replacement before computing the unifier corresponding to σ in S2 .
Finally one has to ensure that it is possible to reconstruct a unifier σ of
S1 ∪ S2 from unifiers σ1 and σ2 of respectively S1 and S2 that have a disjoint
domain (thanks to the assignment of each variable to a theory). Let us explain
? ?
the solution on the example S1 = {f (x) = y} and S2 = {g(y) = x}. The
first non-deterministic steps assign y to E1 and x to E2 , and finds two unifiers
σ1 = {y → f (x)} and σ2 = {x → g(y)}. Thus, in this example:
the constant x occurs in the instance of the variable y
while the constant y occurs in the instance of the variable
x.
The differences in the combination methods proposed are differences in the
treatment of this occur-check problem.
A solution for finitary equational theories. The first method was pre-
sented in the seminal work of Schmidt-Schauß [191] and relies on the existence of
a constant elimination procedure. Such a procedure inputs a sequence of terms
(ti )1≤i≤n and a sequence of free constants (cj )1≤j≤m and computes, whenever
it exists, a most general set Σ of substitutions such that for all σ ∈ Σ, for all
1 ≤ i ≤ n, and for all 1 ≤ j ≤ m the term ti σ is equal to a term ti in which the
constant cj does not occur. The occur-check problem is avoided by choosing
which variable occurs as a subterm of which other variable in a solution.
Assuming that each equational theory is finitary, one first computes a com-
plete set of most general unifiers Σi for Si , for i ∈ {1, 2}. In order to respect
the guessed ordering, a constant x cannot appear in the instance of a variable](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-145-320.jpg)
![146 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
y. The constant elimination procedure is employed to eliminate all occurrences
of constants that do not satisfy this requirement from the unifiers in Σi . The
application of this procedure yields two sets of unifiers Σ1 and Σ2 . For each
couple (σ1 , σ2 ) ∈ Σ1 × Σ2 one can reconstruct a unifier of S1 ∪ S2 by induction
on the guessed ordering (see [191] for the complete proof). Thus we have the
following theorem.
Theorem 8.1. (Schmidt-Schauß, [191]) Let E1 and E2 be two disjoint finitary
equational theories that each has a constant elimination procedure. Then E1 ∪ E2
is a finitary equational theory that has a constant elimination procedure.
Extension to arbitrary equational theories. In order to employ the con-
stant elimination procedure one needs first to compute a finite set of most
general unifiers, which is not possible when the equational theory is infinitary
or nullary. In the same chapter [191], Schmidt-Shauß has provided us with a
way to handle such equational theories. The principle is simple, and consists in
encoding the guessed subterm relation with extra equations in the empty theory.
Instead of replacing a variable x assigned to the signature E1 by a constant in
?
S2 one adds to S2 an equation x = fx (y1 , . . . , yk ), where the yi are the variables
assigned to E2 that shall be smaller than x in the guessed ordering, and fx is a
newly introduced free function symbol. Lemma 4.22, p. 72 is again applicable,
and the addition of these equations ensure that the unifiers of the extended
unification systems can be combined.
Theorem 8.2. (Schmidt-Schauß, [191]) Let E1 and E2 be two disjoint equational
theories that both have a decidable general unifiability problem. Then E1 ∪ E2
has a decidable general unifiability problem.
The presentation of Schmidt-Schauß’ results is heavily influenced by Baader
and Schulz’s article [16] who have greatly simplified the presentation of [191].
They have also proposed another way to encode the guessed subterm relation,
which consists in guessing a total (instead of partial) ordering on the variables
of the problem. The linear constant restriction consists in restricting the ad-
missible unifiers of a unification system to those in which a variable x is not
instantiated by a constant y if x lcr y.
Theorem 8.3. (Baader, Schulz, [16]) Let E1 and E2 be two disjoint equational
theories that both have a decidable unifiability with linear constant restriction
problem. Then E1 ∪E2 has a decidable unifiability with linear constant restriction
problem.
Combining disjoint deduction systems
Given that the satisfiability of a connection is defined w.r.t. the satisfiability of
a unification system it seems at first glance that the results on the combination
of decision procedures for unifiability is sufficient to obtain a procedure combin-
ing decision procedures for the satisfiability of symbolic derivations. There are](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-146-320.jpg)
![8.2. COMBINATION OF DECISION PROCEDURES 147
however differences that need to be taken into account. First, if one abstracts
the deductions of the attacker with contexts—terms in which all function sym-
bols are public symbols— a procedure solving the satisfiability problem has to
check whether there exists contexts such that a unification system is satisfi-
able. Since the HSD does not check whether the attacker performs the same
actions at different times, this problem is a special case of second-order linear
unification (see [109], p. 1043), which is decidable when the equational theory
is empty ([109] refers to [108], but another available source is [143]).
In spite of the fact that the satisfiability of a symbolic derivation is akin to a
linear second-order unification problem (as was presented by M. Baudet in his
thesis [28]), an algorithm that combines decision procedures for second-order
linear unification is not sufficient: applying one such algorithm to a (D1 ∪ D2 )-
satisfiability would not reduce to D1 - and D2 -satisfiability problems but to D1 -
and D2 -second-order linear unification problems. Such a transformation is not
optimal since e.g. in the case of deduction systems for which the equational is
convergent and subterm, the satisfiability and equivalence problems are decid-
able [27], but another special case of second-order linear unification is undecid-
able [12].
However we have successfully employed the recipes that are at the heart of
the definition of oracle rules to derive a combination procedure for satisfiability
p p
problems. Let D1 = (F1 , F1 , E1 ) and D2 = (F2 , F2 , E2 ) be two disjoint deduc-
tion systems, i.e. such that F1 ∩ F2 = ∅. We also let be a simplification
ordering on T (F1 ∪ F2 , X ), and assume that there exist a minimum term for
which is a constant cmin ∈ Cnew .
First we redefine the subterm relation so that the maximal strict subterms
of a term t whose root is a function symbol in Fi are its maximal subterms free
in Ei , for i ∈ {1, 2}. Then we construct the transitive closures D1 and D2 of
the deduction systems D1 and D2 . Without surprise the constructed deduction
systems are local w.r.t. the redefined subterm relation. Assuming that the
trace on the HSD is the substitution σ in normal form, Lemma 4.22 can be
employed to replace σ-free subterms in Sub(Ch ) with the constant cmin ∈ Cnew .
By minimality of cmin every sequence of replacements of a free term by cmin
terminates, and results in a substitution σ such that there exists a (D1 ∪ D2 )-
ASD C and a connection function ϕ such that (C, ϕ) ∈ Ch and σ = TrCh ◦ϕ C (Ch ).
Since every subterm of σ is bound by σ in Sub(Ch ) we then partially guess
a (D1 ∪ D2 )-ASD with less than Sub(Ch ) deduction steps as follows:
• For each term t ∈ Sub(Ch ) we guess to which signature the root symbol
of (tσ )↓ belongs;
• For each deduction step we guess which term t ∈ Sub(Ch ) binds the result
of the deduction;
• Also for each deduction step we guess which deduction system among D1
and D2 is employed to deduce t;
• Finally we guess a connection ϕ between this ASD C and the HSD Ch , and
let C = Ch ◦ϕ C.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-147-320.jpg)
![148 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
We check the soundness of the choices by turning the guessed deduction states
(i.e. those that model the deductions of the attacker) of C into both input and
output states, and by computing two HSDs C1 and C2 which are respectively
D1 - and D2 -ASDs by deleting in Ci the deduction steps in C that originate from
Ch but are not in Di .
The difficult part, detailed in [76] consists in proving that the equations
induced by the choice of the binding term t in the second step are such that
C1 and C2 are still HSDs (modulo the removal of some constants in Cnew ). The
separation of C into C1 and C2 requires a purification of the unification system
of C , which in term requires either the addition of new function symbols if one
wants to employ Theorem 8.2 or the guessing of a linear constant restriction
constraint if one wants to employ 8.3. We have chosen the latter as it does not
require one to change the signature. Using the notations of symbolic derivation,
we have thus proven in [76] the following theorem
Theorem 8.4. (Chevalier, Rusinowitch, [76])?? If the ordered satisfiability
p
problem is decidable for two deduction systems D1 = (F1 , F1 , E1 ) and D2 =
p
(F2 , F2 , E2 ) then the ordered satisfiability problem is decidable for the deduction
system D1 ∪ D2 .
A version for extended deduction systems has also been proved in collabo-
ration with D. Lugiez in [65].
Theorem 8.5. (Chevalier, Lugiez, Rusinowitch, [65]) If the ordered satisfiabil-
p
ity problem is decidable for two extended deduction systems D1 = (F1 , F1 , E1 )
p
and D2 = (F2 , F2 , E2 ) then the ordered satisfiability problem is decidable for the
extended deduction system D1 ∪ D2 .
Note on the ground case. Let us assume Ch is a ground symbolic derivation.
Then, reusing the notations of the above algorithm, for every term t ∈ Sub(Ch )
we have tσ = t, and thus the first two steps of guessing can be performed
deterministically. Since every term of C is bound to a ground term so is every
term in both C1 and C2 . Thus we also have that ground reachability problems
are also modular, a result not written but directly deducible from [70]. A more
precise analysis performed in [11] actually shows that it is not necessary to guess
the symbolic derivation C : assuming the decidability of ground reachability in
each of the deduction systems, the locality of the union of their transitive closure
permits one to perform a least-fixpoint computation of the accessible subterms
of Ch . This argument leads to the definition of a polynomial time combination
procedure for the ground reachability problems.
Application: composition of cryptographic protocols. A secrecy goal
of a cryptographic protocol can be encoded by adding an extra reception to
the HSD representing this protocol in which it is tested whether the message
received is the secret. Accordingly, a cryptographic protocol with secrecy goals
can be represented by a finite set of HSDs, one of the secrecy goal being violated
if, and only if, one of these HSDs is satisfiable.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-148-320.jpg)
![8.2. COMBINATION OF DECISION PROCEDURES 149
Assume that two finite sets of honest symbolic derivations each representing
one cryptographic protocol with secrecy goals are defined over disjoint deduction
p p
systems D1 = (F1 , F1 , E1 ) and D2 = (F2 , F2 , E2 ). A composition with secrecy
goal of these two protocols is defined by a set connection between these symbolic
derivations in which only one of the secrecy goals is selected. By Theorem ??,
one of the composition is satisfiable if, and only if, an HSD in the initial two
sets of HSDs is satisfiable. In plain terms, there is a secrecy attack on the
composition of the two cryptographic protocols if, and only if, there is a secrecy
attack on one of these cryptographic protocols. This result was originally proved
by Ciobaca and Cortier in [82] in the special case of HSDs in which the states
are totally ordered. We note that the extension to extended deduction systems
by using Theorem 8.5 is straightforward.
Note on the linear constant restrictions. Whether for any equational the-
ory E the decidability of E-unifiability implies the decidability of E-unifiability
with linear constant restriction is still an open problem. However we note that
in our combination theorem we require more than the mere decidability of E-
unifiability, and in some cases this extra assumption permits one to encode the
linear constant restrictions into a satisfiability problem.
Let D = (F, F p , E) be a deduction system. We say that D is complete if
p
F = F. Let S be a E-unification system and x1 . . . xn be a linear constant
restriction on the variables and constants of S. We note that S is decidable with
the linear constant restriction if, and only if, the D-HSD CS, constructed as
follows is satisfiable:
• First CS, consists in a sequence of length n of input and output states.
The ith state in this sequence is either
?
– both a knowledge state with associated equation V(i) = xi and an
output state if xi is a constant,
?
– or an input state with the equation V(i) = xi if xi is a variable;
• Then CS, constructs all the terms occurring in S;
• Finally we add, in addition to equations stemming from the knowledge
?
and deduction steps, equations V(i) = V(j) to model the equations in S.
Since the deduction system is complete the attacker can instantiate a variable xi
by any ground term in which only the constants among {x1 , . . . , xi−1 } occur. It
is then trivial that CS, is satisfiable if, and only if, S is satisfied by a substitution
satisfying the linear constant restriction .
Theorem 8.6. Let D be a complete deduction system with equational theory
E. Then if D-satisfiability is decidable then E-unifiability with linear constant
restrictions is decidable.
As a corollary we obtain the fact that for complete deduction systems one
does not need to bother with linear constant restriction constraints.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-149-320.jpg)
![150 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
Corollary 8.1. Let D be a complete deduction system. If D-satisfiability prob-
lems are decidable then D-satisfiability with linear constant restriction problems
are decidable.
In the future I plan to extend Theorem 8.6 to incomplete deduction systems.
I believe that such a result would emphasize the relation existing between sym-
bolic derivations and subterm ordering constraints.
8.2.3 Asymmetric Combination problem
Introduction
Let us recall the question we had concerning the extension of a deduction system
that has a decidable satisfiability problem:
Asymmetric combination problem: Assume that D1 and
D2 are two deduction systems such that D1 -satisfiability problems
are decidable. Are (D1 ∪ D2 )-satisfiability problems decidable ?
Of a course a consequence of the preceding section is that, when D2 and
D1 are disjoint deduction systems, if the satisfiability problems with linear con-
stant restrictions of both systems are decidable then the (D1 ∪ D2 )-satisfiability
problems are decidable. This means we shall examine the case in which the
signatures of D1 and D2 are not disjoint, and thus without loss of generality the
case in which:
p
D1 = (F1 , F1 , E1 )
p
D1 = (F2 , F2 , E2 )
F1 ⊆ F2
p Ep ⊆ E2
1
F1 ∩ F2 = ∅
Hierarchical theories
This section summarizes the joint work with M. Rusinowitch presented in [71,
72]. The starting point is the observation—briefly mentionned in Section 8.1.2—
that in the Dolev-Yao deduction system, composed terms never needed to be
decomposed. In particular we had a distinction between “being decomposed” and
“being employed in a regular decomposition step”. This distinction is justified by
the fact that in the Dolev-Yao equational theory, the replacement of encs (b, c)
by any term t in the term t = decs (encs (a, encs (b, c)), encs (b, c)) commutes with
the normalization of t. However we also note that encs (b, c) is not a free term in
the Dolev-Yao equational theory, and thus Lemma 4.22 cannot be employed as
is to obtain a pumping lemma authorizing the replacement of a free term with
a smaller term.
The difficulty in that work consists in finding a criterion such that:
• the possibility of replacing a subterm is dependent on its position in a
larger term t;](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-150-320.jpg)

![152 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
Preservation by o-completion: in order to preserve the type discipline on
the ordered completion of the theory:
• we extend the mode to variables, which can be of mode 0 or mode 1;
• we require that the arguments of function symbols also have a mode.
In the following we assume that there exists a mode function m(·, ·) such
that m(f, i) is defined for every symbol f ∈ F2 of arity n and every integer i
such that 1 ≤ i ≤ n. For all f, i we have m(f, i) ∈ {1, 2} and for all f ∈ F1 and
for all i, m(f, i) = 1. We partition the set X into two denumerable sets X1 ∪ X2 .
For all f ∈ F2 ∪ X we define a function that gives the signature Sig(f ) to which
a symbol belongs:
sig : F ∪ X ∪ C → {0, 1, 2}
i if f ∈ Fi ∪ Xi for i ∈ {1, 2}
Sig(f ) =
0 otherwise, i.e. when f is a free constant
The function sig is extended to terms by taking T (t) = T (top(t)) where top(t)
is the function symbol at the root of t.
A position p · i in a term t is well-moded if T (t|p·i ) = m(top(t|p ), i). In other
words the position in a term is well-moded if the subterm at that position is of
the expected type w.r.t. the function symbol immediately above it. If a non
root position of t is not well-moded we say it is ill-moded in t. Note also that by
definition every free constant is in a ill-moded position. A term is well-moded if
all its non root positions are well-moded. An equational theory (F, E) is well-
moded if for all equations u = v in E the terms u and v are well-moded and
T (u) =T (v).
One can prove that if an equational theory is well-moded then its completion
is also well-moded [72]. We have tailored the notion of mode so that, in a well-
mode equational theory E, every ill-moded term in normal form can be replaced
by an arbitrary term (Lemma 8 in [72]), thereby regaining a notion of free term
in the equational theory.
The notion of local extension of the deduction system is more difficult to
obtain. On the one hand Hypothesis 1, p. 366 in [72] permits one to obtain the
locality of the deduction system on ground terms. In contrast with the result
on the combination of disjoint deduction systems this result is not sufficient,
given that one has to guess the attacker deductions in D2 before resolving the
D1 -satisfiability problems. Also we have to be able to solve that E2 -specific
equations before solving the pure E1 -unification system. These considerations
lead us to the addition of several hypotheses (quoted here from [72]):
Hypothesis 1: If E →S2 E, r →S2 E, r, t and r ∈ Sub(E, t)∪Cspe
/
then there is a set of terms F such that E →∗ 1 F →S2 F, t.
S](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-152-320.jpg)
![8.2. COMBINATION OF DECISION PROCEDURES 153
Hypothesis 2: For all terms s ∈ S1 , for all substitutions τ such
that (X2 ∩ Var(s))τ is a set of ground terms, and for all ground
terms t there is at most one ground substitution σ such that
sτ σ =H t, and this substitution can be computed.
Hypothesis 3: The equational theory (F, E) is reducible to
(F1 , E1 )
These hypotheses may not be optimal, but:
• first we assume that D2 contains only a finite number of symbols, and thus
that a deduction of D2 can be guessed;
• second we assume that pattern-matching—(hypothesis 2 in [72]), em-
ployed when considering ground satisfiability problems—or unification—
(hypothesis 3 in [72]), employed when considering generic satisfiability
problems— can be reduced to pattern-matching or unification in E1 .
We then obtain the following theorems. Since we allow the computation of
a transitive closure, F p (and decorations thereof) denotes in these theorems a
set of terms.
Theorem 8.7. (Extension of ground satisfiability problems) If:
p
• F2 is finite;
• D1 -ground satisfiability problems is decidable;
• E2 -word problem is decidable;
• Hypotheses 1 and 2 are satisfied.
Then the D2 -ground satisfiability problem is decidable.
Theorem 8.8. (Extension of satisfiability problems) If:
p
• F2 is finite;
• D1 -ordered satisfiability problem is decidable;
• Hypotheses 1 and 3 are satisfied.
Then the D2 -ordered satisfiability problem is decidable.
Extension of the mode to extended deduction systems. Retaining the
main ingredients of the reduction from the decidability of D2 -satisfiability prob-
lems to the decidability of D1 -satisfiability problem we conjecture that the same
reduction can be provided for extended deduction systems if:
• An extended deduction of (tσ)↓ from (t1 σ)↓, . . . , (tn σ)↓ for every ground
substitution σ in normal form must also satisfy that all the terms t, t1 , . . . , tn
are pure F1 - or F2 -terms, and:](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-153-320.jpg)
![154 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
p
– either all the terms are pure F1 -terms, and the rule is in F1 ;
p
– or t is a pure F2 -term, and the rule is in F2 .
• the equational theory satisfies hypothesis 3;
• the deduction system satisfies hypothesis 1;
p
• there is only a finite number of rules in F2 .
Then D2 -satisfiability problems can be reduced to D1 -satisfiability problems.
We note that this conjecture is actually needed to obtain the decidability
result obtained in [57]. Though I believe the proof does not contain any difficulty
it can still be counted as a future research direction.
8.3 Saturation-based decision procedures
8.3.1 A special case of asymmetric combination
Let us consider the case in which F1 = ∅ and thus D1 is empty. Theorem 8.8 in
this case gives a decidability criterion for satisfiability problems. We thus have
the following theorem.
Theorem 8.9. (Decidable class of satisfiability problems) Let D = (F, F p , E)
be a deduction system such that:
• F p is finite;
• D is local;
• E-unification is finitary.
Then the D-satisfiability problem is decidable.
However Theorem 8.9 is in most cases of little use given that it actually re-
quires the locality w.r.t. a subterm relation such that Lemma 4.22, p. 72 can be
applied on every free subterm of a given term. Thus, in the research direction
that has eventually lead to our interest in saturated sets of clauses in first-order
logic, I have worked with Mounira Kourjieh on the practical definition of satu-
rated deduction systems as well as on subclasses having a decidable satisfiability
problem.
I present in Section 8.3.2 the original motivation of our analysis of satu-
rated deduction systems. Then in Section 8.3.3 I present the decidability and
undecidability results obtained for saturated deduction systems.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-154-320.jpg)
![8.3. SATURATION-BASED DECISION PROCEDURES 155
8.3.2 Motivation
When Mounira Kourjieh began her thesis work under my supervision, there
was a lot of research focusing on the relation between concrete and symbolic
models of cryptographic protocols. This research focused more precisely on the
conditions to impose on the concrete cryptographic primitives that ensure the
existence of a symbolic model so that a protocol valid in the symbolic model is
valid in the concrete model. The techniques developed in this area are however
of little help when one wants to prove that, under some additional constraints,
a cryptographic protocol is flawed.
Furthermore, some well-known flaws in existing cryptographic primitives
were uncovered:
• There was a sequence of articles describing meaningful attacks on cryp-
tographic protocols based on collision attacks on MD5 described in [211,
142]: computation of forged X.509 certificates [199], of meaningful postscript
documents having the same image with MD5 [93],. . .
• Also some theoretical works [212, 210] showed some collision computation
on the then thought robust SHA-0 and SHA-1 hash functions.
A practical problem was thus, given an existing cryptographic protocol that
employs one of these hash functions, to determine whether these attacks directly
lead to secrecy, authentication, or any other high-level flaws.
Another similar vulnerability but on digital signature algorithms was known
since [37]. In a multi-user setting, even assuming the strongest (existential
unforgeability) security on the signature algorithm, it is possible to create a key
that appears to have been employed to create a known message/digital signature
pair. This Duplicate Signature Key Selection attack was employed in [20] to
construct an unknown key share attack on a cryptographic protocol. This attack
only relies on the fact that every agent creates his own signature keys, instead
of having a trusted library generating and storing them, and therefore affects
most of the standard signature schemes, including RSA, Rabin, ElGamal, DSA
and ECDSA (see [37], Section 4, with a possible, though costly, mitigation for
ECDSA presented in [127]).
We have stated earlier that relating a concrete cryptographic model to a
symbolic one is difficult given that in the former the impossibility of a com-
putation is assumed while the latter assumes the finite description of all possi-
ble computations. This difficulty turns into an advantage when one considers
flaws in cryptographic primitives, as they are expressed by the existence, in the
concrete setting, of a tractable function. Even when this function only has a
non-negligeable probability of computing the desired result, it can be modeled
in a deduction system by an over-approximation that always yields the desired
outcome. Thus, taking into account the flaws of existing cryptographic primi-
tives during the refutation of cryptographic protocols is easy enough: it suffices
to add new public symbols describing the concrete algorithms employed, and to
relate the application of these functions to other messages by adding equations](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-155-320.jpg)

![8.3. SATURATION-BASED DECISION PROCEDURES 157
the one hand, and of the concatenation on the other hand. The decidability of
the former is trivial. The decidability of the latter is a consequence of the fact
that it suffices to guess which free constants occur in the instance of a variable,
and thus of the fact that unifiability with linear constant restrictions is decidable
for the associative equational theory [193].
Duplicate Signature Key Selection. The subsequent work on the mod-
elling of the Duplicate Signature Key Selection (DSKS) property was along the
same line. The computation of a digital signature key pair is modeled by two
public function symbols v and s (standing respectively for the computation of
the validation and the signature keys) and with the addition of an equation:
valid(x, sign(x)s(y), v (x, sign(x)y)) = true
to the equations modeling that v, s and v , s model validation/signature key
pairs:
valid(x, sign(x)s(y), v(y)) = true
valid(x, sign(x)s (y1 , y2 ), v (y1 , y2 )) = true
All the function symbols but s, v are public. The decidability of satisfiability
problems for this deduction system was presented in [58] and relies on the com-
putation of a saturated deduction system, i.e. a deduction system in which
deductions are modeled by terms instead of symbols, and such that the result of
a composition (i.e. a deduction whose result is not a subterm of the messages
in the input) is never decomposed (we refer to [58] for the exact definitions and
proofs). This work has in our view emphasized the importance of the notion of
saturation, given that finite saturated deduction systems automatically satisfy
the first two points of Theorem 8.9 but w.r.t. the standard subterm relation,
and the last point is normally a pre-requisite for the saturation.
Saturated Deduction Systems. As is the case of ground entailment in first-
order logic, saturated deduction systems always have a decidable ground satisfi-
ability problem [134]. The natural question is then of whether this result can be
lifted to satisfiability problems, i.e. to determine whether satisfiability problems
are decidable for saturated deduction systems and, whien this is not the case,
give minimal restrictions entailing the decidability of satisfiability problems.
It turned out that the answer to the first question is negative: we have
provided the encoding of the runs of a deterministic Turing machine such that
the attacker can compute a message m (encoding the halt in an accepting state
of the Turing machine) if, and only if, he can compute an accepting run of
the Turing machine. Applying this result on the encoding of a universal Turing
machine thus yields the undecidability of the satisfiability problem for saturated
deduction systems.
We have nonetheless provided a criterion that ensure decidability which is
based on the structure of the terms in the saturated deduction system. It is in
nature similar to the definition of S + (Definition 3.17 in [18]):](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-157-320.jpg)
![158 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
Definition 47. (Class S + , [18], p. 1807) A clause set S belongs to S + if for all
clauses C in C and all litterals L in C:
1. if t is a functional term occurring in L then Var(t) = Var(C);
2. | Var(L)| ≤ 1 or Var(L) = Var(C).
While our criterion lacks the simplicity of the class S + it is tailored to en-
sure that every sequence of unification between literals of the clauses in a local
derivation eventually terminates. This guarantee is provided by imposing, in-
tuitively, that guessing the application of a saturated deduction rule will either
strictly decrease the number of variables in the unification system of a sym-
bolic derivation representing partially the deductions of the intruder, or will
not instantiate the terms in this unification systems prior to the guess of the
deduction. Accordingly we call the saturated deduction systems meeting these
restrictions contracting. We refer the reader to [134] for the exact definition and
proofs.
8.4 Research Directions
My work on the refutation of cryptographic protocols lead me to two different
research directions:
• first, the importance of saturation leads to the analysis of saturated deduc-
tion systems in the more general setting of sets of clauses, instead of just
sets of Horn clauses, which would be the natural generalization of deduc-
tions. We have already presented some preliminary results in Section 5.2,
p. 81;
• second, there is a more complex asymmetry issue related to deduction
systems. While the saturation of deduction systems enables us to derive
decidability results, they are unsatisfactory since these results are conse-
quences of the decidability of more complex problems, and thus saturation
does not permit one to obtain fine decidability results for the satisfiability
problems.
In order to make the second point clear, let us consider subterm deduction
systems, i.e. deduction systems such that the equational theory is subterm
convergent. It is known that:
• a variant of saturation [134] always terminate on subterm deduction sys-
tems, but the resulting deduction system are not contracting;
• the decidability of satisfiability for subterm deduction systems relies heav-
ily on the fact that initially, all the terms in the knowledge of the intruder
are ground;
• general constraints, i.e. those for which the initial knowledge is not
ground, are undecidable in general for subterm deduction systems.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-158-320.jpg)
![8.4. RESEARCH DIRECTIONS 159
Thus, while saturation may help one in deriving new decidability results for
the satisfiability problem, we believe that more attention should be paid on the
structure of these problems.
Example 28. In particular I think the combination result of [70] gives us a more
abstract characterization of satisfiability problems as the natural generalization
of reachability problems for infinite state transition systems. To establish this
assume one is given an infinite-state transition system as follows:
• a fixed initial state, modeled by a term t0 ;
• a finite set of transitions of the form τ : s → s , such that there exists a
transition from a state t to a state t if there exists a ground substitution
σ such that sσ = t and s σ = t ;
• the set of goal states is the set of all ground instances sf σ of a term sf .
The combination result of [70] implies that to modularly decide reachability for
such transition systems one needs to solve ordered satisfiability problems for the
deduction system defined with:
• the unary public symbols fτ ;
• the (convergent) equational theory fτ (s) = s for every transition τ .
A similar remark was also described in [48], where instead of reachability prob-
lems the authors consider proofs with holes, i.e. proofs in which parts have been
erased. That remark may be more natural, given that the erasure of some de-
ductions is exactly what happens when one tries to modularly prove a theorem.
Example 29. Consider a set of clauses S = {C1 , . . . , Cn }. By turning the
predicate symbols into function symbols, introducing a multiset operator +
that has the following properties:
x + (y + z) = (x + y) + z
x+y = y+x
x+0 = x
and one unary function symbol neg, one can encode the clauses C1 , . . . , Cn as
terms t1 , . . . , tn , the empty clause being encoded with the term 0. Let us add two
public function symbols f and r of respective arity 1 and 2, with the equations:
f (x + x + y) = f (x + y)
r(x + y, neg(x) + z) = y+z
Finally, consider the equational theory ES constructed as follows, with a new
constant :
n
ES = ti =
i=1](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-159-320.jpg)
![160 CHAPTER 8. CRYPTOGRAPHIC PROTOCOLS REFUTATION
The completeness and correctness of resolution implies that the set S is unsat-
isfiable if, and only, for the following symbolic derivation:
? ?
C = ({1, 2}, {1 → x, 2 → y}, {x = , y = 0}, { , 0}, {2}, {1})
we have C = ∅.
This encoding may seem unnecessary given that we have merely reported
the difficulty of deciding whether a given set of clauses is unsatisfiable into the
equational theory. However having a uniform framework to reason on terms,
atoms, clauses and deductions provides in my view a theoretical basis for “de-
modulation across argument and literal boundaries,” a research problem posed
by [217].
8.5 Conclusion
I have summarized in this chapter a large part of my research since I started
a Ph.D. In particular I have tried to emphasize the connections between the
different problems I have considered, sometimes sacrificing the “unimportant”
details that would have helped the reader not familiar with this work. In this
form, however, this summary outlines the extent with which the results obtained
are closely tied to basic or standard results in first-order logic.
While reachability or proof finding problems can be analyzed in isolation,
it seems more rewarding to obtain composable decidability results. I believe
that to obtain this modularity decidability results have to been obtained on
the (ground) satisfiability problems for deduction systems, and not only on
reachability problems or proof finding problems. As a consequence I believe
that satisfiability problems we have considered hitherto only in the context of
cryptographic protocol refutation should actually be considered as interesting
objects of analysis, in themselves, instead of just by-products of cryptographic
protocol refutation.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-160-320.jpg)

![162CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
C l i ent G o al
signatureRequest(session(sid),certificate(name,ckey),contract(data))
signaturePolicy(session(sid),policy(footer))
signature(session(sid),SIGNATURE)
SIGNATURE = signature(crypt(inv(ckey),apply(sha1,pair(data,footer))))
signatureResponse(session(sid),TIMESTAMP,ASSERTIONS)
TIMESTAMP = timestamp(time,PROOF,#2,crypt(inv(#2),PROOF)))
PROOF = apply(md5,pair(time,apply(md5,SIGNATURE)))
C l i ent G o al
Figure 9.1: Time stamping and archiving a digital signature
Digital Contract Signing (DCS)[14], how it succeeds within seconds in deriving
a composed service that is currently proposed as a product by the OpenTrust
Company.
Furthermore we propose to automatically generate a ready-to-deploy web
archive, corresponding to a prudent implementation of the newly composed
web service.1
Introductory example
Figure 9.1 illustrates a composition problem corresponding to the creation of a
new service (described here by Goal ) for appending a time stamp to a digital
signature performed by a given partner (described here by Client) over some
data (described here by data) and then submitting it together with the signed
data and some other proofs for long time conservation by an archiving third
party. More precisely Goal should expect a first message from Client containing
a session identifier sid, the Client’s certificate containing his identity and his
public key ckey and finally the data he wishes to digitally sign. Goal should
answer with a message containing the same session identifier and a footer value
to be appended to the data before the client’s signature. This value aims to
capture the fact that the Client acknowledges a certain chart (known by Goal )
1 Currently we really generate these implementations in terms of ready-to-deploy web ap-
plications, invoking real services but there is still some work to do before claiming we generate
them in high compliance with Web Services Standards.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-162-320.jpg)

![164CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
A ny Servi ce CA
loop
CVRequest(mode)
alt [mode = OCS P]
certificate(name,key)
assertion(OCSPR,cakey,crypt(inv(cakey),OCSPR))
OCSPR = ocspr(name,key,time)
alt [mode = CRL]
currentCRL(crl)
A ny Servi ce CA
Figure 9.2: Available services: Certification Authority
instance Figure 9.2 describes a certification authority CA capable of providing
two sorts of answers when asked about the validity of a certificate: one is OCSP -
based (i.e. based on the Online Certificate Status Protocol) and returns a proof
containing a real-time time-bound for the validity of a given certificate; while the
second only provides the classical Certificate Revocation List CRL. Intuitively
by inspecting the composition problem one can think that to satisfy the Client
request the second mode should always be employed with CA (provided it is
also trusted by the Client). One can also deduce that some adaptation should
be employed over the Client’s messages to obtain the right message patterns
(possibly containing assertions) from the community (for example the use of
the flag OCSP with CA).
The solution we propose computes whenever it is possible the sequence of
calls to the service community possibly interleaved with adaptations over the
already received messages and permitting to satisfy the Client’s requests as
specified in the composition problem.
The remainder of this chapter is organised as follows: in Section 9.1.2, we
present our model for web services and we formally state the composition prob-
lem and its solution. In Section 9.1.3, we present our ongoing work on the](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-164-320.jpg)
![9.1. TRACE-BASED SYNTHESIS OF AN ORCHESTRATION 165
synthesis of a ready-to-deploy prudent implementation of the newly obtained
composed service. In Section 9.1.4, we present our work on translating the for-
mal description of the mediator of the obtained composed service to ASLan in
order to permit its validation against regular security properties. We conclude
in Section 9.1.5.
9.1.2 Mediator synthesis
A web service is in standard way described in terms of the interface it presents
to the outside world (the possible clients) using the WSDL [187] language. This
description is structured into ports, each proposing a set of available operations.
An operation is then defined by the given of its in-bound and out-bound message
patterns; these patterns are usually described using the XSD [203] language and
reflects the XML message structure. Security constraints can then be defined
on top of the service interface description using WS-Security [172] annotations.
Such annotations can occur at any level in the WSDL binding the levels they
occur into the security constraints they carry. They range from the service to
the message level and typical examples are an SSL transport requirement for
the whole service or the need to cipher or digitally sign a certain part inside
a message pattern (in-bound or out-bound to some operation). We note that
the use of XSD for the description of message patterns permits the use of the
XPATH [215] language to write the queries identifying parts inside these mes-
sage patterns which simplifies the writing of message-level security constraints.
We put the focus on SOAP-based (in contrast with RESTful-based) web ser-
vices. These services rely on the SOAP [87] protocol that encapsulates the
messages described in the WSDL specification of the service. We claim that
after (automated) analysis we can collect from the different specification files
the descriptions of the different message patterns in-bound and out-bound to
all the operations of the service and corresponding to the messages really ex-
changed by the service (SOAP encapsulation included). These descriptions are
discussed below.
Representation of messages and security constraints
We aim to represent a significant fragment of XML messages as described by the
XSD language using first-order terms defined over a signature given below. The
fragment we address corresponds to XML elements, described by sequential
complex types, i.e. elements having an ordered and a fixed-cardinality set of
children. We also abstract away the attributes in XML messages. To represent
XML messages we define the following signature:
F = {noden , childn | i ≤ a ∈ N, n ∈ C} ∪
a i
a
{scrypt, sdcrypt, crypt, dcrypt, sign, verif, inv, invtest, }
where the symbol noden represents an XML node named n (ranging over a set of
a
constants C) and having a children. For each symbol noden we define the set of
a](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-165-320.jpg)
![166CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
symbols childn , . . . , childn permitting to extract its children. In order to model
1 a
a a
security constraints holding over exchanged XML messages, we also represent
the usual cryptographic primitives through the use of symbols: scrypt/sdcrypt
for symmetric encryption and decryption, crypt/dcrypt for asymmetric encryp-
tion and decryption, sign/verif for digital signature and its verification, inv
to denote key inverses and invtest permitting to test whether a pair of terms
{t, t } verifies t = inv(t). The constant is the result of a successful test. We
denote by Fp , the set of public symbols and assume in the remainder of this
chapter that Fp = F {inv}.
Some of the symbols represent the possible operations on the messages. Their
semantics is defined with the following equational theory:
sdcrypt(scrypt(x, y), y) = x (Ds )
dcrypt(crypt(x, y), inv(y))
= x (Das )
EXM L verif (x, sign(x, inv(y)), y) = (Sv )
childn (noden (x , . . . , x )) = xi (P a )
i
i a 1 a
a
invtest(x, inv(x)) = (Iv )
Representation of services
We note that the WSDL specification of a web service does not precise any order
of invocation for its operations but only gives their exhaustive list. Moreover
this specification does not mention how the input parameters are related to
the output parameters for a given operation. The BPEL [171] language allows
reasoning about such properties by permitting first to specify a certain work-
flow logic for the service, and second to specify all the manipulations needed
to construct the sent messages given the received ones. In this sense BPEL de-
scribes business processes which are structured workflows of activities ranging
over invocation of web service operations, providing of web services operations
or manipulation of messages.
We assume that all the services we consider are also described in terms
of their respective BPEL specification and focus only on services described by
linear processes, i.e. sequences of activities. Therefore a service S will be consid-
ered as a sequence of in- and out-bound messages denoted respectively RCV (m)
and SN D(m) as described by the following grammar:
P, Q := services
0 null service
RCV (m) · P input message
SN D(m) · P output message
P Q AC parallel composition
Parallel composition of services S1 and S2 is denoted by S1 S2 . It is
associative and commutative, and has a unit element 0, the null process. We
consider a community to be a parallel composition of all its available services.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-166-320.jpg)

![168CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
In other word we have to check for the existence of a derivation (applying
the transition rules) from an initial state (S = (Π1 | · · · |Π2 , ∅), to a state where
all requests from the client have been satisfied (C has ended) and the services
from the community that have been initiated have properly terminated.
Solving the composition problem
Theorem 9.1. The Service Composition Problem is NP-complete.
Sketch of proof: We reduce the Service Composition Problem to showing the
existence of an attack on a protocol built from the services and the client (given
the EXM L theory). To ensure proper termination of services that are involved
in an interaction with the client, we guess at the beginning whether a service Si
will be employed or not. Let {S1 , . . . , Sm } be the subset of services to be really
employed. After this guessing step the composition problem is reduced to the
reachability of a configuration (0, E) from a configuration (C S1 . . . Sm , ∅)
with {S1 , . . . , Sm } ⊆ {S1 , . . . , Sn }
For each service S in {C, S1 , . . . , Sm } we introduce a new constant cS and
transform the service S into a service S = S · SN D(cS ). It is clear that a
service S reduces to the null process if, and only if, S sends cS . Finally we add
a monitor service M to the community that checks that all constants are sent.
We let
M = RCV (cC ) · RCV (cS1 ) . . . RCV (cSm ) · SN D(secret)
It is also clear that M sends secret if and only if all the services C, S1 , . . . , Sm
reduce to the null process. Thus we have transformed the problem of the reach-
ability of a configuration (0, E) from a configuration (C S1 . . . Sm , ∅) into
the problem of the reachability of a configuration (P, E ) with secret ∈ E from
the initial configuration (M C S1 . . . Sm , ∅). This latter problem is a
classic problem for cryptographic protocols and is called the Protocol insecurity
problem. Since the existence of an attack on a protocol is a problem known to
be in NP [190] we can conclude.
The protocol insecurity problem corresponding to our composition problem
can then be submitted to any state-of-the-art protocol verification tool capable
of checking reachability properties. If the composition problem admits a solution
we obtain an attack trace describing how the intruder (or the mediator from
a composition point of view) succeeded into satisfying the clients requests by
applying its adaptation skills on messages exchanged with some services in the
community.
For instance Figure 9.3 illustrates the solution for the composition problem
stated in the introductory example. The mediator obtains a time stamp from a
time stamper (denoted by TS ) trusted by the Client then obtain an assertion
from the certification authority CA stating the validity of the time stamper’s
certificate. He also calls CA to obtain similar assertions about an archiving third
party service’s (denoted by ARC ) and the Client’s certificates. Finally he calls](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-168-320.jpg)
![9.1. TRACE-BASED SYNTHESIS OF AN ORCHESTRATION 169
the archiving tier service to obtain the last needed assertion before successfully
answering the last request of the Client.
At this level we already decided the feasibility of the composition given
the Client’s requests and the community of available services. We propose to
further the study to first, obtain an operational implementation of the new fea-
ture provided by the composed service (or mediator) and second to validate
this implementation against regular security properties (and in prescript of all
other partner services). We already reached the second objective and enabled
it in the Avantssar validation platform: the description of the mediator is auto-
matically extracted from the attack trace and then translated to ASLan using
the Trace2ASLan module. The mediator’s ASLan specification together with
the specifications of the Client and the involved services from the community
can then be submitted to the Avantssar platform for validation. Details about
Trace2ASLan are described in Section 9.1.4 while we present in Section 9.1.3
our ongoing work on the first objective.
9.1.3 Mediator prudent implementation
We present in this section our approach for generating a prudent implementa-
tion of the mediator obtained after solving a web service composition problem as
explained in Section 9.1.2. The remainder of this section is organised as follows:
first we define a target for web service implementation and one of its important
desired properties: prudence. Informally speaking this notion requires that the
implementation checks its input messages as thoroughly as possible (for example
by checking all the correlation possibly existing between received messages or
by proceeding to all the possible verifications of digital signatures). Finally we
present our linear-time procedure to generate a prudent implementation for a
given web service described using the web services model we introduced in Sec-
tion 9.1.2 which we apply to generate prudent implementation for composition
mediators.
Implementation for web services
We first present some extensions to our web services model before introducing
the notion of implementation. Terms are manipulated by applying operations
on them. These operations are defined by a subset Fp of the signature F
called the set of public symbols. A context C[x1 , . . . , xn ] is a term in which all
symbols are public and such that its nullary symbols are the variables x1 , . . . , xn .
C[x1 , . . . , xn ] is also denoted C when there is no ambiguity and n is called its
length.
Definition 48. A strand s is a finite sequence of messages each with ! or ?
label. Messages with label ! (respectively, ?) are said to be “sent” (respectively,
“received”). A strand is positive if and only if all its labels are ?. The length of
! !
a strand s = ? m1 , . . . , ? mn is n, and its input is denoted by input(s) and is the
strand (?r1 , . . . , ?rn ) where r1 , . . . , rn is the ordered sub-sequence of messages
labelled by ? in s.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-169-320.jpg)
![170CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
! !
We denote by si (respectively, by si ) the prefix ( ? m1 , . . . , ? mi ) (respectively,
?
the labelled message ! mi ). We also define σs as the ground substitution {xi →
input
mi }1≤i≤n and σs as the restriction of σs to the set {xi | si =?mi }. To
model the initial knowledge IK(s) of the web service, represented by the strand
s, we prefix s with a reception ?t for every term t in IK(s). We assume in the
following that ∈ IK(s) for all strands s.
Definition 49. Given a strand s, a context C and a ground term t, we say that
input input
C evaluates to t on s if and only if Var(C) ⊆ Supp(σs ) and Cσs =EXM L t.
Next we give an operational semantics to the send and receive activities
defined by a strand.
Definition 50. An unification system S is a finite set of equations denoted by
?
(ui = vi )i∈{1,...,n} with terms ui , vi ∈ T (F, X ). It is satisfied by a substitution
σ, and we note σ |= S, if for all i ∈ {1, . . . , n} ui σ =EXM L vi σ.
Active frames. Strands are given an operational semantics with active frames—
a simple process model in which the computation of messages to send and the
verification on the received messages are specified. The notation ?ri (respec-
tively, !ei ) refers to a message stored in variable ri (respectively, ei ) which is
received (respectively, sent). Let us recall the definition of active frames.
Definition 31, p. 100. An active frame is a sequence (Ti )1≤i≤k where
?
!ei with ei = Ci [r1 , . . . , ri−1 ] (send)
Ti = or
?ri with Si (r1 , . . . , ri ) (receive)
where Ci [r1 , . . . , ri−1 ] denotes a context and Si a unification system over vari-
ables rj 1≤ji . A variable ri (respectively, ei ) is called an input variable (re-
spectively, an output variable) of the active frame.
Definition 32, p. 101. Let ϕ = (Ti )1≤i≤k be an active frame as in Defini-
tion 31 and where the input variables are r1 , . . . , rn . Let s be a positive strand
!M1 , . . . , !Mn , σϕ,s be the substitution {ri → Mi } and S be the union of the
unification systems in ϕ. The evaluation of ϕ on s is denoted ϕ · s and is the
strand (mi )1≤i≤k where:
!Ci [m1 , . . . , mi−1 ] If Ti is !ei
mi =
?ri σϕ,s If Ti is ?ri
We say that ϕ accepts s if Sσϕ,s is satisfiable.
Definition 33, p. 101. An active frame ϕ is an implementation of a strand s if
ϕ accepts input(s) and ϕ·input(s) =E s. If a strand s admits an implementation
we say this strand is executable.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-170-320.jpg)



![174CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
We let for all t in RST (s), Cmin (s, t) = context(γmin (s, t)) and define for all i in
{1, . . . , n} the following unification system over variables {x1 , . . . , xi } ∪ {yt | t ∈
RSTi (s)}
?
Ui (s) = {Cmin (s, t) = C | C ∈ Ci (s, t) {Cmin (s, t)}}
t∈RSTi (s)
In the remainder Un (s), when n is the length of s, is also denoted by U(s).
Theorem 9.3. Let s be a strand of length n. For all step 1 ≤ i ≤ n let
t1 , . . . , tk(i) be the enumeration of elements in RSTinew (s) such that:
Cmin (s, t1 ) R(s) . . . R(s) Cmin (s, tk(i) )
We define:
• τs,i = {yt1 → Cmin (s, t1 )} ◦ . . . ◦ {ytk(i) → Cmin (s, tk(i) )}
• τ s,i = τs,1 ◦ . . . ◦ τs,i
For all step i in {1, . . . , n} we have:
1. the context Cmin (s, t)τ s,i evaluates to t on si for all t in RSTi (s);
2. Ui (s)τ s,i is a finite basis of si .
The main argument in proof of Theorem 9.3 is the GivanM92 [118] of the
EXM L theory. This permits to solve the general reachability problem by consid-
ering only its restriction to the subterms of a given strand. In the remainder we
present algorithms that compute the unification systems {Ui (s)}1≤i≤n and the
mappings {τ s,i }1≤i≤n given a strand s of length n, which permits to compute
the finite bases for {si }1≤i≤n as stated in Theorem 9.3. Moreover our algorithms
provide for all t in RSTi (s) the contexts Cmin (s, t). Together with {τ s,i }1≤i≤n
these contexts permits to provide extraction contexts from s for all t in RST (s).
Therefore if all si+1 labelled with ! in s are reachable from si , we can provide a
prudent implementation of s as stated in Theorem 9.2.
Concrete algorithms
Let us first introduce the data structures for terms (including the special case
of contexts and thereby unification systems), sequents and strands. Then we
will present the principle of Algorithms 9.1 and 9.2.
Arrays and queues. We use FIFO queues and arrays to hold terms and
sequents objects. We employ an object-oriented notation. Given an array
object A, A.add(t) adds the element t to the array and returns its index,
A.nbelements() returns the number of elements in the array A and A[i] re-
turns the element stored at index i in A if i ≤ A.nbelements(). Given a FIFO
queue Q, Q.pop() consumes and returns the first element in Q, while Q.push(o)](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-174-320.jpg)
![9.1. TRACE-BASED SYNTHESIS OF AN ORCHESTRATION 175
appends o to its end and A.nbelements() returns the number of elements in the
queue Q. We note that all operations described above can be implemented in
constant time. Given a queue or an array O, we let O.size() be the sum of the
sizes of all the objects hold by O.
Representation of terms. A set of terms S is stored in an array A of term
objects. Each term t ∈ S is represented by a term object with fields:
id: integer identifying t. We require that A[i].id = i for all 1 ≤ i ≤ A.nbelements()
symbol: element of F representing the head symbol of t
dst: array of id ’s of its ordered maximal strict subterms
context: integer identifying the context Cmin (s, t)
sequents: queue holding identifiers of sequents where t appears in the left-hand
side
inv: identifier of inv(t) in A if inv(t) is a subterm of s.
In Algorithm 9.1 a test of the form t = f (t1 , . . . , tn ) is equivalent to test whether
t.symbol = f , and if the test is positive all ti are assigned to t.dst[i]. We define
the size of a term t to be the size of the term object holding t, i.e. the sum of
all the sizes of its fields enumerated above.
Representation of contexts and unification systems. Similarly a set
of contexts is stored in an array C of context objects where each context is
represented by a context object, which is the sub-record of the term object
?
having only the symbol and dst fields. An equation C = C is then represented
by a pair of integers (idC , idC ) where idC , idC are the indexes of the context
objects representing the contexts C, C in C, and a unification system U is
represented by a queue holding all the representations of the equations in U .
Representation of strands. A strand s = ( ? mi )1≤i≤n is represented by
!
the couple (A, IO) where A is the representation of ST (s) and IO is an array
holding the couples (mi .id, ? )1≤i≤n in order. The size of s denoted by |s| is
!
defined as A.size() + IO.size().
Representation of sequents. A sequent γ is represented by a record having
the following fields:
id: integer identifying γ
rhs: integer identifying the right-hand side of the sequent
symbol: element of Fp and representing the head symbol of the context of γ
lhs: array of term identifiers (id ) in the left-hand side of γ](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-175-320.jpg)
![176CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
ready: integer representing the number of occurrences of terms in the left-hand
side of γ that are not yet reachable and initially set to the arity of the
head symbol in context
In the following, we also use the notation t1 .id, . . . , tn .id f t.id as a shortcut
to the structure holding the sequent t1 , . . . , tn f t.
Computation of S(s) Given a representation (A, IO) of strand s, our goal
is to compute an array S holding a representation of each sequent in S(s) and
to update the sequents queue for all elements in A. The update is performed
on the global arrays A and S by the register method:
method register(id1 , . . . , idn f id)
cr ← S.add(id1 , . . . , idn f id)
for all k ∈ {1, . . . , n} do A[idk ].sequents.push(cr) end for
return cr
end method
Algorithm 9.1: Computation of S(s)
1: S ←∅
2: for all t ∈ A do
3: switch t do
4: case t = scrypt(m, k)
5: S.register(m.id, k.id scrypt t.id)
6: S.register(t.id, k.id sdcrypt m.id)
7: case t = crypt(m, k)
8: S.register(m.id, k.id crypt t.id)
9: S.register(t.id, k.inv dcrypt m.id)
10: case t = sign(m, inv(k))
11: S.register(m.id, inv(k).id sign t.id)
12: S.register(m.id, t.id, k.id verif .id)
13: case t = inv(t)
14: S.register(t.id, t .id invtest .id)
15: case t = noden (t1 , . . . , ta )
a
16: S.register(t1 .id, . . . , ta .id noden t.id)
a
17: for all i ∈ {1, . . . , a} do
18: S.register(t.id childn ti .id)
i
a
19: end for
20: end switch
21: end for
22: return S
Principle of Algorithm 9.1. Given a strand s in normal form, and for each
term t ∈ ST (s) we perform a case analysis on its structure to compute the](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-176-320.jpg)
![9.1. TRACE-BASED SYNTHESIS OF AN ORCHESTRATION 177
sequents; we then insert these sequents into S using the register method above.
Note that each subterm t of s contributes to S(s) by a number of sequents only
depending of its head symbol, and therefore the value S.nbelements() can be
computed beforehand and is linear in the size of input (A, IO). In fact S does
not yet contain sequents in S(s) with empty left-hand side. These sequents are
finally added to S by Algorithm 9.2.
Complexity of Algorithm 9.1. The outermost loop runs through the sub-
terms of s stored in A. Algorithm 9.1 processes each subterm t of s in a number
of constant-time instructions linear w.r.t. the size of t which permits us to state
its time-linearity w.r.t. to the size of s.
Computation of the Ui (s). Given the representations (A, IO) of a strand
s of length n and S of S(s) we compute an array C representing the contexts
in C(s) and arrays I, U representing the prudent implementation of s and such
that for all 1 ≤ i ≤ n:
1. if si =!mi then I[i] is the index of the context object Cmin (s, mi )τ s,i in
C4;
2. if si =?mi then U[i] is a queue representing the unification system Ui (s)τ s,i .
Algorithm 9.2 relies on the register2 procedure that updates the global array C.
method register2(f [id1 , . . . , idn ])
cr ← C.add(f [A[id1 ].context, . . . ,S[idn ].context])
return cr
end method
Principle of Algorithm 9.2. From the array of sequents S output by Algo-
rithm 9.1, Algorithm 9.2 computes iteratively the terms that are reachable in
strand s, for each reception step. If a labelled message si =!mi is such that mi
is reachable in s then an extraction context of mi in s is stored in I. Hence
the computation of I permits us to simulate the call to an oracle Ar by taking
Ar (si−1 , mi ) = I[i] for si =!mi . Similarly array U stores the extraction contexts
of the reachable subterms in s (at each step) and can be employed to build a
finite basis for s and its prefixes by taking Ab (si ) = U[i].
Correction of Algorithm 9.2. The correction of Algorithm 9.2 is based on
the fact that the order in which it inserts contexts satisfies the properties P1–P3
imposed on R(s) .
4 The minimum here is taken with respect to the order
Q introduced in Correction of
Algorithm 9.2.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-177-320.jpg)
![178CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
Algorithm 9.2: Computation of the Ui (s)τ s,i
1: S ← Output of Algorithm 9.1
2: C,Q,step ← ∅, ∅, 0
3: for all mi ∈ IO do
4: step++
5: if mi = (idi ,?) then
6: Q.push(S.add( xi idi ))
7: while Q = ∅ do
8: seq ← Q.pop()
9: t ← S[seq.rhs.id]
10: ind = register2(seq.symbol[seq.lhs])
11: if t.context = null then
12: t.context ← ind
13: while t.sequents = ∅ do
14: seq’ ← S[t.sequents.pop()]
15: seq’.ready−−
16: if seq’.ready = 0 then
17: Q.push(seq’)
18: end if
19: end while
20: else
21: U[step].push((t.context,ind))
22: end if
23: end while
24: else if mi = (idi ,!) then
25: I[step] ← A[idi ].context
26: end if
27: end for
28: return I, U, C
Complexity of Algorithm 9.2. Given a strand s each sequent γ in S(s) is
at most popped once into the queue Q (only when γ.ready = 0). Moreover,
each time such a sequent is processed, the algorithm also runs through all the
elements in rhs(e).sequents and elements in lhs(e). As previously explained in
complexity of Algorithm 9.1 the first processing is linear-time w.r.t. the size of
the strand s whereas the second processing is linear w.r.t. the size of the strand
s. Therefore Algorithm 9.2 runs in linear-time complexity w.r.t. to the DAG
size of its input.
Experiments
The compilation procedure presented above has been tested on several web ser-
vice composition problems. As a preliminary work we succeeded into generating
from a composition problem the prudent implementation for its corresponding](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-178-320.jpg)
![9.1. TRACE-BASED SYNTHESIS OF AN ORCHESTRATION 179
mediator and for all the involved services from the community. These imple-
mentations have been realised in Java and deployed as Java Servlets performing
the communications corresponding to each service and thus enabling the Client
to successfully interact with the mediator. This permitted us to verify in a real
setting our compilation procedure and to obtain a first realisation of the new
feature brought by the composed service. We note that the need for generating
also the services involved in the composition (they are supposed to be already
implemented and running) is due to the Servlet architecture choice: we some-
how bound the messages format and the communication between services to a
setting different from web services standards. We currently further this work in
order to generate web services compliant realisations for the mediators: in this
setting the generated mediator communicates directly with the already existing
web services in a standard way.
9.1.4 Mediator validation
In this section we show how we obtain an executable specification of the mediator
in terms of the Avantssar Specification Language (ASLan) [13]. ASLan is a
formal language for specifying security-sensitive service-oriented architectures,
the associated security policies, as well as their trust and security properties.
ASLan specifications can be validated (in the Dolev-Yao intruder model) using
back-ends from Avantssar Platform [15]. Hence our translation allows us to
verify several security properties of the mediator such as confidentiality and
authentication.
Modelling Web Services in ASLan
We translate strands into ASLan roles. An ASLan role is defined by a transition
system and an initial state. States are sets of facts, where facts can be thought
of as first order terms over a given signature. The transition rules are of the
form l ⇒ r where l and r are states. There is a transition from a state s to
a state s whenever there exists a transition rule l ⇒ r and a substitution σ
such that lσ ⊆ s and s = (s lσ) ∪ rσ. The facts in a state s can encode the
reception or the emission of a message (e.g. iknows(scrypt(m, k))). The state
of the web service is encoded with a fact state wrap(x1 , . . . , xn ) where each xi
is associated with a reachable subterm of the strand we translate. The language
allows also to guard the transitions by conditions like equality or disequality
between first order terms.
Generating an ASLan specification for the mediator
The approach proposed in this section has been implemented in Java. The
designed component called Trace2ASLan takes as input a strand representation
of web service and outputs in linear time the specification of the corresponding
ASLan role.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-179-320.jpg)
![180CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
Handling Knowledge. A strand of even length s = [?s1 !s2 . . .?sn−1 !sn ] is
translated into a set of rules. We assume the existence of an injective function
name mapping each term in RST (s) to a unique string.
We assume that each reception is followed by a response, and compile each
sub-sequence ?s2j−1 !s2j of s into a transition rule. We reuse the notations Si
and Ci of Definition 31. The internal state of the agent executing the mediator
is modelled by a term state wrap of arity k, where k is the number of terms in
RST (s). At each step i a variable val(i, t) that represents the current value of
t ∈ RST (s) in the state is computed as follows:
X name(t) if t ∈ RSTk (s)
val(k, t) =
Y name(t) otherwise
We translate each couple ?si−1 !si in the strand with the generic pattern:
state wrap(val(i − 2, t1 ),...,val(i − 2, tm ), i − 1).
iknows(val(i − 1, si−1 )) ? equal(t, t )
t=t ∈Si−1
⇒
state wrap(val(i, t1 ),...,val(i, tm ), i + 1).
iknows(Ci )
Initial knowledge and nonces. We have a special translation for the initial
sequence of values received in the strand that correspond to the parameters
for the execution and the nonces. We create an initial state that contains a
state wrap term for each instance of a strand. The value of t ∈ RST (s) in this
term is either ⊥ if t is not a nonce or a parameter, or the ground term actually
used as a parameter.
Example 32. The ASLan specification corresponding to the web service de-
scribed by the strand ?scrypt(m, k)?k!m is:
section signature:
state_wrap: nat * msg * symmetric_key * msg - fact
section types:
t,Y_T,X_T,m,Y_M,X_M: message
k,Y_K,X_K: symmetric_key
section inits:
initial_state init :=
state_wrap(t,k,m,1)
section rules:
step s1_(Y_T,Y_K,Y_M,X_T) :=
state_wrap(Y_T,Y_K,Y_M,1).
iknows(X_T)](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-180-320.jpg)

![182CHAPTER 9. WEB SERVICES ORCHESTRATION CHOREOGRAPHY
extract operations that was used and each agent can deploy a corresponding
service (with fixed operations).
Similar cooperation problems have often been addressed in previous work
[32, 33, 45, 164, 178] and solved by methods ranging from automata synthesis
to AI planning or logic programming. Our objective here is to contribute to
the state of the art by solving some cases, not considered before, where the
structure of messages matters and where the security policy of each agent is an
additional constraint. It is a non trivial task to find a cooperation scheme. Since
some agents may not trust each other, they may have their own requirements
to communicate, and some intermediates may be required to intervene (e.g. to
provide certificates).
We represent the communicating agents abstractly by specifying them solely
by their initial knowledge (what an agent knows in the beginning of the inter-
action) and their goals (what he wants to obtain). The agent may create a
new knowledge from what he knows at some point: at each point of the execu-
tion, the agent’s knowledge is closed under pairing, encryption, decryption (if
he knows the key), signing, etc. The agent ability to cooperate takes the form
of sending and receiving of messages. But some restrictions are to be imposed:
• agents may not accept any message, but only those with some pre-defined
pattern (this expresses his policy);
• agents can only send the messages they can create from their knowledge;
• an agent cannot communicate directly with another agent if the two do
not share a communication channel.
Note that we can parametrise the initial knowledge of the agents, e.g. we can
say that and agent knows something encrypted with a given key but without
specifying what exactly is encrypted. In this case the problem would be to find
values that instantiate an initial knowledge of every agent together with the
communication that satisfies all the goals
9.2.2 Book publishing
We give an instance of the problem (see Figure 9.4): a writer (Agent A1 ) wants
to publish his new book (t). There is an enterprise that, besides others services,
has a Publishing (Printing) Service (Agent A4 ). This service accepts to print
only books approved by a Writing Style Authority (Agent A3 ). Anyone outside
this enterprise is forbidden to access directly the Printing Service. To get access
one has to contact the “Reception” (Agent A2 ) of this enterprise. The Reception
can communicate with the Printing Service: they share a key and the Printing
Service accepts only messages encrypted with that key.
In this case, the network topology is as follows: A1 , A2 , A3 are pairwise con-
nected (as they represent public entities); A2 and A4 also have a communication
channel (as they belong to the same enterprise).](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-182-320.jpg)






![9.3. CONCLUSION 189
Composition rules Decomposition rules
t1 , t2 → (encs (t1 , t2 ))↓ encs (t1 , t2 ), (t2 )↓ → (t1 )↓
t1 , t2 → (encp (t1 , t2 ))↓ encp (t1 , t2 ), (priv(t2 ))↓ → (t1 )↓
t1 , t2 → ( t1 , t2 )↓ t1 , t2 → (t1 )↓
t1 , priv(t2 ) → (sign(t1 )priv(t2 ))↓ t1 , t2 → (t2 )↓
t1 , . . . , tm → (· (t1 , . . . , tm ))↓ · (t1 , . . . , tm ) → (ti )↓ for all i
Table 9.2: DY+ACI deduction system rules
Decidability
Theorem 9.4. Satisfiability of a constraint system within DY+ACI is decidable
and is in NPTIME.
Proof sketch. First we can show that it suffices to consider normalised con-
straint systems and normalised models. Then we prove the existence of a con-
servative solution of satisfiable constraint system: it can be built using only
quasi-subterms (some subset of subterms) of the constraint system. This gives
us a bound on the size of such a solution, and, therefore, decidability. Due to
the polynomial complexity of normalisation algorithm and also the polynomial
complexity of a check t ∈ Der(E), where t and E are ground and normalised,
we obtain NP as a class of complexity for the initial problem.
Theorem 9.5. Satisfiability of a constraint system within DY is decidable and
is in NPTIME.
Proof. The main idea is to build a solution within DY+ACI deduction system
(as DY signature is strictly included into DY+ACI signature, as well as DY
deduction system is strictly included into DY+ACI one), and then replace ACI
lists in the solution with nested pairs: · ({t1 , . . . , tn }) is replaced by t1 , . . . , tn .
The resulting substitution will still be a model of the initial constraint system.
Thus we have the same complexity as for DY+ACI case.
Full proofs of these theorems are given in [12].
9.3 Conclusion
The work described in this chapter is still under progress. We currently focus on
the automated deployment of synthesized services as Web Services. A prelimi-
nary version written by Mohammed Anis Mekki deploys the existing services as
well the newly generated one on a Tomcat server. These services then communi-
cate by relying on the Tomcat server for the service to service communications,
and implement an instance manager that forwards the messages to the correct
instance of the service. Our choice on communication implies that we are in-
dependent from the SOAP security layer, which we believe is a drawback to
inter-operability. Future work will concentrate on the deeper integration into
the standard SOAP Web Service Architecture.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-189-320.jpg)

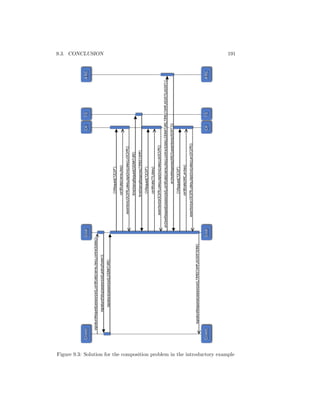

![Chapter 10
Equivalence of
Cryptographic Protocols
My first published article on the equivalence of cryptographic
protocols was written in collaboration with M. Rusinowitch [75]
and consisted in a reformulation of Mathieu Baudet’s proof of
decidability of trace equivalence for subterm deduction systems.
In this chapter I present a criterion that encompasses saturation
deduction systems ?? as well as subterm deduction systems.
That work was also presented at the Secret 2010 workshop. The
notion introduced is the one of finitary deduction systems. It
intuitively corresponds to deduction systems such that there
exists a lazy solving algorithm in the spirit of [8]. We prove that
the equivalence of symbolic derivations is decidable for finitary
deduction systems.
10.1 Introduction
Context. Security protocols are designed to provide communication means
between several parties in a way that ensures that some information is protected.
Well-known stories about flaw discoveries [147] have revealed that protocols may
be subject to unexpected and undesirable behaviours under malevolent attackers
actions. Formal analysis of protocols is therefore mandatory for gaining the level
of confidence required in critical applications. Formal methods and related tools
have proved to be successful to some extent for this task. But they are limited
in expressiveness since in most cases authors were focused on the resolution
of reachability problems, and as a consequence very few effective procedures
consider the more general case of equivalence properties.
Motivations. Observational equivalence is a crucial notion for specifying se-
curity properties such as anonymity or secrecy of a ballot in vote protocols [96].
193](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-193-320.jpg)
![194 CHAPTER 10. EQUIVALENCE OF CRYPTOGRAPHIC PROTOCOLS
For instance observational equivalence can justify that there is no action for
an attacker that makes distinguishable two protocol executions with different
identities or vote values.
To be of effective use the notion of observational equivalence should be con-
sidered on processes modeling cryptographic protocols. We consider in this
chapter a setting in which the actions of the are represented by one HSD and
those of a unique intruder by one ASD (see Chapter 6 for more details). Sym-
bolic derivations can be seen as standing between symbolic traces [27] and the
simple cryptographic processes of [89].
The only decidability result on the equivalence of symbolic traces (called
S-equivalence) we are aware of is for the class of subterm deduction systems
and was given by M. Baudet [27, 28]. We have recently given another proof of
this result [73] on which this chapter elaborates. A more efficient procedure is
presented in [54] when one considers only the Dolev-Yao deduction system. In
spite of the relevance of this problem for the analysis of e.g. voting protocols, we
are not aware of any extension of Baudet’s decidability results to other classes
of deduction systems.
Applications. The equivalence notion we consider in this chapter has two
straightforward applications, one related to the symbolic validation of crypto-
graphic properties and one related to the search for on-line guessing attacks.
An on-line attack is one in which the attacker interacts with honest agents to
achieve his goals which usually are the acquisition of a previously unknown piece
of data, or the impersonation of a honest agent. In these cases the achievability
of a goal can be reduced to a reachability problem. However one may consider
goals for which this reduction does not hold. For example, the dictionnary
attacks introduced by Schneier [192] consist in guessing a piece of data (usually
a password) and interacting with the honest agents with this piece of data.
Depending on the resulting communication the attacker knows whether the
guess was correct. It is often the case that such attacks can be detected by
the honest agents involved. For example, sending a wrong password will be
detected by an authentication system that, after a small number of failure, may
invalidate the account and ask for a new password. To take into account this
possible response by honest agents, Ding and Horster [105] have introduced the
concept of undetectable on-line guessing attacks. They consider that a protocol
is vulnerable to this kind of attacks whenever (i) the honest agents cannot
distinguish between a session with the right piece of data with one involving a
wrong guess whereas (ii) the intruder can distinguish the two executions. We
model the first point by stating that the tests performed by the honest agents
succeed in both cases, and the second point by saying that the two executions
are not equivalent.
Recent works initiated by Abadi and Rogaway in 2000 [7] have shown that
computational proofs of indistinguishability ensuring the security of a protocol
can be derived, under some natural hypothesis on cryptographic primitives, from
symbolic proofs. This has opened the path to the automation of computational](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-194-320.jpg)
![10.2. FINITARY DEDUCTION SYSTEMS 195
proofs. It was shown by [86] that in presence of an active attacker observational
equivalence of the symbolic processes can be transfered to the computational
level.
Related works. Many works have been dedicated to proving correctness
properties of cryptographic protocols using equivalences on process calculi. In
particular framed bisimilarity has been introduced by Abadi and Gordon [6]
for this purpose, for the spi-calculus. Another approach that circumvents the
context quantification problem is presented in [42] where labelled transition
systems are constrained by the knowledge the environment has of names and
keys. This approach allows for more direct proofs of equivalence.
To the best of our knowledge, the first tool capable of verifying equivalence-
based secrecy is the resolution-based algorithm of ProVerif [39] that has been
extended for handling equivalences of processes that differ only in the choice of
some terms in the context of the applied π-calculus [40]. This allows to add some
equational theories for modelling properties of the underlying cryptographic
primitives. The more recent YAPA tool [29] also permits one to evaluate the
indistinguishability of two constraint systems that are essentially equivalent to
symbolic derivations, but it still lacks an associated decision procedure.
Few decidability results are available. In the article [125] H¨ttel proves
u
decidability for a fragment of the spi-calculus without recursion for framed
bisimilarity. In [89] the authors show how to apply the result by Baudet on
S-equivalence to derive a decision procedure for observational equivalence for
subterm convergent theories for simple processes. Since [89] relies on the proof
of Baudet’s result, that is long and difficult [28], we believe that a direct self-
contained approach as the one presented below might be valuable too.
Organization of this chapter. We reuse in this chapter the notions and no-
tations for terms, equational theories, deduction systems, and symbolic deriva-
tions introduced in earlier chapters. We assume that the equational theory
considered is consistent, i.e. has a model with more than one element1 . The
main result of the chapter is proved in Section 10.3, namely that equivalence of
symbolic derivations is decidable for finitary deduction systems.
10.2 Finitary Deduction Systems
An equational theory E is finitary whenever every E-unification system has
a finite set of more general unifiers. We define in this subsection an analog
for deduction systems w.r.t. symbolic derivations rather than just equational
theories w.r.t. unification systems. In order to guide the reader we introduce the
concepts we define by relating them to the analoguous concept for equational
theories.
1 Note that in an inconsistent equational theory all terms are equal, all unification systems
are satisfied by any substitution, and two symbolic derivations are equivalent if, and only if,
they have the same structure on their input and output states.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-195-320.jpg)



![10.3. DECIDABILITY OF SYMBOLIC EQUIVALENCE FOR FINITARY DEDUCTION SYSTEMS199
Proof. Assume min (S) ⊆ Ch and let CI be in S. By definition of the ordering
there exists a derivation CI ∈ min (S) and a stutter-free derivation Cc such that
Cc ◦ CI = CI . By hypothesis we have CI ∈ Ch . By Lemma 10.1 this implies
that CI is also in Ch .
Complete sets of solutions. The ordering plays the same role w.r.t. the
solutions of a HSD as the instantiation ordering on substitutions w.r.t. the
solutions of an unification system. In particular the traditional notion of most
general unifier is translated into a notion of minimal solution.
Definition 64. (Complete set of solutions) A set Σ of ASDs is a complete set
of solutions of an HSD Ch whenever:
• Σ ⊆ Ch ;
sf
• for every ASD CI ∈ Ch there exists an ASD Cm ∈ Σ and a stutter free
ASD Cc such that Cm ≤ CI ◦ Cc .
We have departed from our line of translating terms from the unification
framework to the symbolic derivation framework by introducing a symbolic
derivation Cc . It permits us to consider cases in which the computation of a
complete set of unifiers introduces unnecessary deduction steps in individual
ASDs. A common example of such addition is the normalisation of messages
t, t , i.e. the automatic deduction of the two messages t and t even when they
are not useful to the attacker.
10.2.3 Finitary deduction systems
We have already noted that a NP decision procedure for the satisfiability of
HSDs for the Dolev-Yao deduction system is known since [190]. While this
procedure is based on the guessing of an attack of minimal size, other proce-
dures have been proposed [8, 161] that instead cover all possible stutter-free
derivations [66], i.e. compute a complete set of solutions. We define deduction
systems for which such a procedure exists to be finitary.
Definition 65. (Finitary Deduction Systems) Let I be a deduction system. If
there exists a procedure that computes for every I-HSD Ch a finite complete set
of solutions we say that I is a finitary deduction system.
10.3 Decidability of Symbolic Equivalence for
Finitary Deduction Systems
This section is devoted to the proof of the main theorem of this paper.
Theorem 10.1. Symbolic equivalence is decidable for finitary deduction sys-
tems.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-199-320.jpg)







![Chapter 11
Research project
• to work on the potential applications to safety analysis;
• to explore further the relation between reachability anal-
ysis and first-order automated reasoning techniques;
• to obtain a comprehensive framework for service compo-
sition that also takes into account trust negotiation, and
as a consequence to relate more formally the models for
protocols and Web Services presented in this document;
• to extend the modularity results obtained to address the
modular verification of aspect-based programs.
The third point is a straightforward continuation of the research
I have presented in this document. I accordingly focus this
chapter on the remaining points.
11.1 From security to safety
It has been advocated in [145] that security should not be an additional layer
around the protected system, but instead every system should be built with its
security in mind. A striking example is the case of malwares: it is futile to try
to detect the malware the users install, whether knowingly or not, on a system.
Sooner or later, a user will try to install one malware, and sooner or later, one
of the installed malware will not be detected in time. Accordingly, the problem
is not to detect or define what a malware is, but to ensure that no user-installed
software can alter in any way the proper functioning of the operating system.
This paper has launched a serie of works, both academic and industrial.
First, an operating system with security in mind was devised [?]. Then, and
in order to access a larger public, mandatory access control was implemented
within the linux kernel to provide anyone interested with a Security Enhanced
Linux, i.e. a free operating system that could be really secured.
207](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-207-320.jpg)
![208 CHAPTER 11. RESEARCH PROJECT
In parallel, the concepts or spatial and temporal segregation, initially formal-
ized by John Rushby in [?] where reintroduced in modern computing environ-
ments through virtualization. One can run each piece of software in a virtualized
operating system, i.e. an operating system standard in every aspect but on the
fact that it runs not on the machine’s hardware, but on an abstraction of it. A
host operating system orchestrate the different application, and ensures when
possible the time segregation between the guest OS. The advantage of this ar-
chitecture is that a flaw in one application is contained in the virtual OS in
which it is run.
The security provided by such systems is not optimal given that the host
operating system can be almost any off-the-shelf one, and thus is itself prone
to suffer from a large number of security issues. A decisive step towards secure
operating systems was the proposal of the Multiple Independent Levels of Se-
curity (MILS) architecture. There, the virtualization part is kept, but the host
operating system is merely a scheduler whose primary role is to ensure that no
information passes from one application to another. The first OS to be certified
at common criteria EAL-71 abides by this architecture. An important point is
that it was the security evaluation was aimed to prove safety objectives. Though
one can argue that the modularity achieved by this system is proper to aircraft
systems regulation2 , I have chosen to view this as an indicator of a long term
trend in safety analysis, in which the safety objectives to be validated will be
the same as the standard security objectives.
These development raise questions on the research in security:
If industrials know enough to produce high-quality and certified
operating systems, what is left to researchers ?
Though one could argue that researchers can focus on securizing the casual users
operating systems instead of highly critical ones. However good ideas tend to
spread3 , e.g. Google’s Chrome browser also implements some spatial segregation
under the name of sandboxing, and it seems more promising to assume that the
kernel is secure, and to focus on the problems left by this assumption:
• First the communications of the machine with its environment also have
to be secured, and thus the protocols securing these communications also
have to be validated;
• Second, the above description was over-simplified and has omitted the
communications between the applications running in the guest operat-
ing systems. These cannot be disregarded as even though they violate
the spatial separation principle, they are often mandatory for the proper
functioning of the system. Accordingly, in addition to being a scheduler,
1 The target was the implementation of the ARINC 653 1-2 scheduler and the segregation
recommended in the RTCA DO-178B at level A
2 in particular the reusability of off-the-shelf components introduced by the RTCA DO-297
3 Who would have bet, 10 years ago, that 74% of the computers (a.k.a. smartphones) sold
in september 2010 were either running linux or FreeBSD (actually a variant of. . . ) ?](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-208-320.jpg)

![210 CHAPTER 11. RESEARCH PROJECT
A natural question for aspect-oriented programs is whether they can be
validated modularly. In addition to the combination results I have obtained,
there has been a lot of work on the combination of rewriting system since the
seminal termination counter-example presented by Toyama [205]. Given that
in e.g. the Avantssar project we have given a rewriting-based semantics to
some aspect-based programms, namely Web Services, I believe it will be very
interesting to relate the modularity techniques developped for rewriting logics
to the usual ways an aspect is woven into an existing program. The benefit of
this approach is clear, as it would suffice to validate programms incrementally
as aspects are added to enrich it.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-210-320.jpg)
![Bibliography
[1] 14th IEEE Computer Security Foundations Workshop (CSFW-14 2001),
11-13 June 2001, Cape Breton, Nova Scotia, Canada. IEEE Computer
Society, 2001.
[2] Proceedings of the 22nd IEEE Computer Security Foundations Sympo-
sium, CSF 2009, Port Jefferson, New York, USA, July 8-10, 2009. IEEE
Computer Society, 2009.
[3] Robinson J. A. A machine-oriented logic based on the resolution principle.
J. Assoc. Comput. Mach., 12:23–41, 1965.
[4] Mart´ Abadi and V´ronique Cortier. Deciding knowledge in security pro-
ın e
tocols under equational theories. In Josep D´ Juhani Karhum¨ki, Arto
ıaz, a
Lepist¨, and Donald Sannella, editors, ICALP, volume 3142 of Lecture
o
Notes in Computer Science, pages 46–58. Springer, 2004.
[5] Mart´ Abadi and C´dric Fournet. Mobile values, new names, and secure
ın e
communication. In Proceedings of the Principle of Programming Lan-
guages Conference, pages 104–115, 2001.
[6] Mart´ Abadi and Andrew D. Gordon. A calculus for cryptographic pro-
ın
tocols: The spi calculus. In ACM Conference on Computer and Commu-
nications Security, pages 36–47, 1997.
[7] Martin Abadi and Phillip Rogaway. Reconciling two views of cryptog-
raphy (the computational soundness of formal encryption). J. Cryptol.,
20(3):395–395, 2007.
[8] Roberto M. Amadio and Denis Lugiez. On the reachability problem in
cryptographic protocols. In Catuscia Palamidessi, editor, CONCUR, vol-
ume 1877 of Lecture Notes in Computer Science, pages 380–394. Springer,
2000.
[9] Anne Anderson. Web services profile of xacml (ws-xacml) version 1.0.
Available at http://www.oasis-open.org/committees/download.php/
24951/xacml-3.0-profile-webservices-spec-v1-wd-10-en.pdf,
2007.
211](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-211-320.jpg)
![212 BIBLIOGRAPHY
[10] S. Andova, C.J.F. Cremers, K. Gjøsteen, S. Mauw, S.F. Mjølsnes, and
S. Radomirovi´. A framework for compositional verification of security
c
protocols. Information and Computation, 206:425–459, February 2008.
[11] Mathilde Arnaud, V´ronique Cortier, and St´phanie Delaune. Combining
e e
algorithms for deciding knowledge in security protocols. In Boris Konev
and Frank Wolter, editors, FroCos, volume 4720 of Lecture Notes in Com-
puter Science, pages 103–117. Springer, 2007.
[12] Tigran Avanesov, Yannick Chevalier, Michael Rusinowitch, and Mathieu
Turuani. Satisfiability of General Intruder Constraints with and without
a Set Constructor. Research Report RR-7276, INRIA, 05 2010. http:
//hal.inria.fr/inria-00480632/en/.
[13] AVANTSSAR. Deliverable 2.1: Requirements for modelling and ASLan
v.1. Available at http://www.avantssar.eu, 2008.
[14] AVANTSSAR. Deliverable 5.1: Problem cases and their trust and security
requirements. Available at http://www.avantssar.eu, 2008.
[15] AVANTSSAR. Deliverable 4.1: AVANTSSAR Validation Platform v.1.
Available at http://www.avantssar.eu, 2009.
[16] Franz Baader and Klaus U. Schulz. Unification in the union of disjoint
equational theories: Combining decision procedures. J. Symb. Comput.,
21(2):211–243, 1996.
[17] Leo Bachmair and Harald Ganzinger. Non-clausal resolution and superpo-
sition with selection and redundancy criteria. In Andrei Voronkov, editor,
LPAR, volume 624 of Lecture Notes in Computer Science, pages 273–284.
Springer, 1992.
[18] Leo Bachmair and Harald Ganzinger. Resolution theorem proving. In
Robinson and Voronkov [188], pages 19–99.
[19] Michael Backes, Markus D¨rmuth, Dennis Hofheinz, and Ralf K¨sters.
u u
Conditional reactive simulatability. Int. J. Inf. Sec., 7(2):155–169, 2008.
[20] J. Baek, K. Kim, and T. Matsumoto. On the significance of unknown
key-share attacks: How to cope with them? In Proc. of Symposium on
Cryptography and Information Security (SCIS 2000), 2000.
[21] Philippe Balbiani, Yannick Chevalier, and Marwa El Houri. A logical ap-
proach to dynamic role-based access control. In Danail Dochev, Marco
Pistore, and Paolo Traverso, editors, Artificial Intelligence: Methodology,
Systems, and Applications, 13th International Conference, AIMSA 2008,
Varna, Bulgaria, September 4-6, 2008. Proceedings, volume 5253 of Lec-
ture Notes in Computer Science, pages 194–208. Springer, 2008.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-212-320.jpg)
![BIBLIOGRAPHY 213
[22] Philippe Balbiani, Yannick Chevalier, and Marwa El Houri. A logi-
cal framework for reasoning about policies with trust negotiations and
workflows in a distributed environment. In Anas Abou El Kalam, Yves
Deswarte, and Mahmoud Mostafa, editors, CRiSIS 2009, Post-Proceedings
of the Fourth International Conference on Risks and Security of Internet
and Systems, Toulouse, France, October 19-22, 2009, pages 3–11. IEEE,
2009.
[23] Gergei Bana, Koji Hasebe, and Mitsuhiro Okada. Computational seman-
tics for basic protocol logic - a stochastic approach. In Iliano Cervesato,
editor, ASIAN, volume 4846 of Lecture Notes in Computer Science, pages
86–94. Springer, 2007.
[24] Gilles Barthe, Marion Daubignard, Bruce Kapron, Yassine Lakhnech, and
Vincent Laporte. On the equality of probabilistic terms. In Proceedings
of the 17th LPAR conference, page (to appear). Voronkov editions, 2009.
[25] David Basin and Harald Ganzinger. Automated complexity analysis based
on ordered resolution. J. ACM, 48(1):70–109, 2001.
[26] David A. Basin and Harald Ganzinger. Complexity analysis based on
ordered resolution. In LICS, pages 456–465, 1996.
[27] Mathieu Baudet. Deciding security of protocols against off-line guess-
ing attacks. In Vijay Atluri, Catherine Meadows, and Ari Juels, editors,
ACM Conference on Computer and Communications Security, pages 16–
25. ACM, 2005.
[28] Mathieu Baudet. S´curit´ des protocoles cryptographiques : aspects logi-
e e
ques et calculatoires. Th`se de doctorat, Laboratoire Sp´cification et V´-
e e e
rification, ENS Cachan, France, January 2007.
[29] Mathieu Baudet, V´ronique Cortier, and St´phanie Delaune. Yapa: A
e e
generic tool for computing intruder knowledge. In Ralf Treinen, editor,
Rewriting Techniques and Applications, 20th International Conference,
RTA 2009, Bras´ ılia, Brazil, June 29 - July 1, 2009, Proceedings, volume
5595 of Lecture Notes in Computer Science, pages 148–163. Springer, 2009.
[30] Moritz Y. Becker, C´dric Fournet, and Andrew D. Gordon. SecPAL:
e
Design and semantics of a decentralized authorization language. Technical
Report MSR-TR-2006-120, Microsoft Research, September 2006.
[31] Mihir Bellare and Phillip Rogaway. Optimal asymmetric encryption. In
EUROCRYPT, pages 92–111, 1994.
[32] D. Berardi, D. Calvanese, G. De Giacomo, R. Hull, and M. Mecella. Auto-
matic Composition of Transition-based semantic Web Services with Mes-
saging. In Proc. 31st Int. Conf. Very Large Data Bases, VLDB 2005,
pages 613–624, 2005.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-213-320.jpg)
![214 BIBLIOGRAPHY
[33] D. Berardi, D. Calvanese, G. De Giacomo, M. Lenzerini, and M. Mecella.
Automatic Composition of e-Services that export their Behavior. In Proc.
1st Int. Conf. on Service Oriented Computing, ICSOC 2003, volume 2910,
2003.
[34] Vincent Bernat and Hubert Comon-Lundh. Normal proofs in intruder
theories. In Okada and Satoh [174], pages 151–166.
[35] Elisa Bertino, Jason Crampton, and Federica Paci. Access control and
authorization constraints for ws-bpel. In ICWS, pages 275–284. IEEE
Computer Society, 2006.
[36] Pierre Bieber. A logic of communication in hostile environments. In
Proceedings of the Computer Security Foundations Workshop, pages 14–
22, 1990.
[37] Simon Blake-Wilson and Alfred Menezes. Unknown key-share attacks on
the station-to-station (sts) protocol. In Hideki Imai and Yuliang Zheng,
editors, Public Key Cryptography, volume 1560 of Lecture Notes in Com-
puter Science, pages 154–170. Springer, 1999.
[38] Bruno Blanchet. An efficient cryptographic protocol verifier based on
prolog rules. In CSFW [1], pages 82–96.
[39] Bruno Blanchet. Automatic proof of strong secrecy for security protocols.
In IEEE Symposium on Security and Privacy, pages 86–. IEEE Computer
Society, 2004.
[40] Bruno Blanchet, Mart´ Abadi, and C´dric Fournet. Automated veri-
ın e
fication of selected equivalences for security protocols. In LICS, pages
331–340. IEEE Computer Society, 2005.
[41] Bruno Blanchet and Andreas Podelski. Verification of cryptographic pro-
tocols: Tagging enforces termination. In Andrew D. Gordon, editor, FoS-
SaCS, volume 2620 of Lecture Notes in Computer Science, pages 136–152.
Springer, 2003.
[42] Michele Boreale, Rocco De Nicola, and Rosario Pugliese. Proof techniques
for cryptographic processes. In LICS, pages 157–166, 1999.
[43] Francois Bronsard and Uday S. Reddy. Conditional rewriting in focus. In
M. Okada, editor, Proceedings of the Second International Workshop on
Conditional and Typed Rewriting Systems, volume 516 of Lecture Notes
in Computer Science. Springer-Verlag, 1991.
[44] T. Brown. A Structured Design Method for Specialized Proof Procedures.
Phd, California Institute of Technology, 1974.
[45] Tevfik Bultan, Xiang Fu, Richard Hull, and Jianwen Su. Conversation
specification: a new approach to design and analysis of e-service compo-
sition. In WWW, pages 403–410, 2003.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-214-320.jpg)
![BIBLIOGRAPHY 215
[46] Alan Bundy, editor. Automated Deduction - CADE-12, 12th Interna-
tional Conference on Automated Deduction, Nancy, France, June 26 -
July 1, 1994, Proceedings, volume 814 of Lecture Notes in Computer Sci-
ence. Springer, 1994.
[47] Sergiu Bursuc and Hubert Comon-Lundh. Protocol security and alge-
braic properties: decision results for a bounded number of sessions. In
Ralf Treinen, editor, Proceedings of the 20th International Conference on
Rewriting Techniques and Applications (RTA’09), volume 5595 of Lec-
ture Notes in Computer Science, pages 133–147, Bras´ ılia, Brazil, 2009.
Springer.
[48] Sergiu Bursuc, Hubert Comon-Lundh, and St´phanie Delaune. Deducibil-
e
ity constraints. presentation at the 2010 Secret Workshop, 2010.
[49] Carlos Caleiro, Luca Vigan`, and David A. Basin. On the semantics of
o
alicebob specifications of security protocols. Theor. Comput. Sci., 367(1-
2):88–122, 2006.
[50] Ran Canetti. Universally composable security: A new paradigm for cryp-
tographic protocols. In Proceedings of the 42nd Foundations Of Computer
Science conference, pages 136–145, 2001.
[51] Ulf Carlsen. Generating formal cryptographic protocol specifications. Se-
curity and Privacy, IEEE Symposium on, 0:137, 1994.
[52] Iliano Cervesato. The logical meeting point of multiset rewrit-
ing and process algebra. Technical report, University of Stan-
ford, 2004. Unpublished manuscript. Available electronically from
http://theory.stanford.edu/?iliano/forthcoming.html.
[53] Chin-Liang Chang and Richard Char-Tung Lee. Symbolic Logic and Me-
chanical Theorem Proving. Academic Press, 1973.
[54] Vincent Cheval, Hubert Comon-Lundh, and St´phanie Delaune. A deci-
e
sion procedure for proving observational equivalence. In Michele Boreale
and Steve Kremer, editors, Preliminary Proceedings of the 7th Interna-
tional Workshop on Security Issues in Coordination Models, Languages
and Systems (SecCo’09), Bologna, Italy, October 2009. accepted to IJ-
CAR 2010.
[55] Yannick Chevalier. R´solution de Probl`mes d’Accessibilit´ pour la Com-
e e e
pilation et la V´rification de Protocoles Cryptographiques. PhD thesis,
e
Universit´ Henri Poincar´ Nancy I, LORIA, december 2003.
e e
[56] Yannick Chevalier. A simple constraint solving procedure for protocols
with exclusive or. In Workshop on Unification (in conjunction with IJCAR
2004), 2004.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-215-320.jpg)
![216 BIBLIOGRAPHY
[57] Yannick Chevalier and Mounira Kourjieh. A symbolic intruder model for
hash-collision attacks. In Okada and Satoh [174], pages 13–27.
[58] Yannick Chevalier and Mounira Kourjieh. Key substitution in the sym-
bolic analysis of cryptographic protocols. In Vikraman Arvind and Sanjiva
Prasad, editors, FSTTCS 2007: Foundations of Software Technology and
Theoretical Computer Science, 27th International Conference, New Delhi,
India, December 12-14, 2007, Proceedings, volume 4855 of Lecture Notes
in Computer Science, pages 121–132. Springer, 2007.
[59] Yannick Chevalier and Mounira Kourjieh. On the decidability of (ground)
reachability problems for cryptographic protocols (extended version).
CoRR, abs/0906.1199, 2009.
[60] Yannick Chevalier, Ralf K¨sters, Micha¨l Rusinowitch, and Mathieu Tu-
u e
ruani. Deciding the security of protocols with commuting public key en-
cryption. Electr. Notes Theor. Comput. Sci., 125(1):55–66, 2005.
[61] Yannick Chevalier, Ralf K¨sters, Micha¨l Rusinowitch, and Mathieu Tu-
u e
ruani. An np decision procedure for protocol insecurity with xor. Theor.
Comput. Sci., 338(1-3):247–274, 2005.
[62] Yannick Chevalier, Ralf K¨sters, Micha¨l Rusinowitch, and Mathieu Tu-
u e
ruani. Complexity results for security protocols with diffie-hellman expo-
nentiation and commuting public key encryption. ACM Trans. Comput.
Log., 9(4), 2008.
[63] Yannick Chevalier, Ralf K¨sters, Micha¨l Rusinowitch, Mathieu Turu-
u e
ani, and Laurent Vigneron. Extending the dolev-yao intruder for analyz-
ing an unbounded number of sessions. In Matthias Baaz and Johann A.
Makowsky, editors, CSL, volume 2803 of Lecture Notes in Computer Sci-
ence, pages 128–141. Springer, 2003.
[64] Yannick Chevalier, Luca Compagna, Jorge Cuellar, Paul Hankes Drielsma,
Jacopo Mantovani, Sebastian M¨dersheim, and Laurent Vigneron. A
o
High-Level Protocol Specification Language for Industrial Security-
Sensitive Protocols. September 2004. Presented at the SAPS’04 Work-
shop, co-located with ASE 2004.
[65] Yannick Chevalier, Denis Lugiez, and Micha¨l Rusinowitch. Towards an
e
automatic analysis of web service security. In Boris Konev and Frank
Wolter, editors, Frontiers of Combining Systems, 6th International Sym-
posium, FroCoS 2007, Liverpool, UK, September 10-12, 2007, Proceed-
ings, volume 4720 of Lecture Notes in Computer Science, pages 133–147.
Springer, 2007.
[66] Yannick Chevalier, Denis Lugiez, and Micha¨l Rusinowitch. Verifying
e
cryptographic protocols with subterms constraints. In Nachum Dershowitz
and Andrei Voronkov, editors, LPAR, volume 4790 of Lecture Notes in
Computer Science, pages 181–195. Springer, 2007.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-216-320.jpg)
![BIBLIOGRAPHY 217
[67] Yannick Chevalier and Micha¨l Rusinowitch. Combining Intruder The-
e
ories. In Lu´ Caires, Giuseppe F. Italiano, Lu´ Monteiro, Catuscia
ıs ıs
Palamidessi, and Moti Yung, editors, Automata, Languages and Program-
ming, 32nd International Colloquium, ICALP 2005, Lisbon, Portugal,
July 11-15, 2005, Proceedings, volume 3580 of Lecture Notes in Computer
Science, pages 639–651. Springer, 2005.
[68] Yannick Chevalier, Ralf K¨sters, Micha¨l Rusinowitch, and Mathieu Tu-
u e
ruani. An NP Decision Procedure for Protocol Insecurity with XOR. In
18th IEEE Symposium on Logic in Computer Science (LICS 2003), 22-25
June 2003, Ottawa, Canada, Proceedings, pages 261–270. IEEE Computer
Society, 2003.
[69] Yannick Chevalier, Ralf K¨sters, Micha¨l Rusinowitch, and Mathieu Tu-
u e
ruani. Deciding the Security of Protocols with Diffie-Hellman Exponenti-
ation and Products in Exponents. In Paritosh K. Pandya and Jaikumar
Radhakrishnan, editors, FST TCS 2003: Foundations of Software Tech-
nology and Theoretical Computer Science, 23rd Conference, Mumbai, In-
dia, December 15-17, 2003, Proceedings, volume 2914 of Lecture Notes in
Computer Science, pages 124–135. Springer, 2003.
[70] Yannick Chevalier and Micha¨l Rusinowitch. Combining intruder theories.
e
In Lu´ Caires, Giuseppe F. Italiano, Lu´ Monteiro, Catuscia Palamidessi,
ıs ıs
and Moti Yung, editors, ICALP, volume 3580 of Lecture Notes in Com-
puter Science, pages 639–651. Springer, 2005.
[71] Yannick Chevalier and Micha¨l Rusinowitch. Hierarchical combination of
e
intruder theories. In Pfenning [176], pages 108–122.
[72] Yannick Chevalier and Micha¨l Rusinowitch. Hierarchical combination of
e
intruder theories. Information and Computation, 206:352–377, 2008.
[73] Yannick Chevalier and Micha¨l Rusinowitch. Decidability of equivalence of
e
symbolic derivations. Submitted to the Journal of Automated Reasoning,
2009.
[74] Yannick Chevalier and Micha¨l Rusinowitch. Compiling and securing
e
cryptographic protocols. Inf. Process. Lett., 110(3):116–122, 2010.
[75] Yannick Chevalier and Micha¨l Rusinowitch. Decidability of the equiva-
e
lence of symbolic derivations. Journal of Automated Reasoning., page (to
appear), August 2010.
[76] Yannick Chevalier and Micha¨l Rusinowitch. Symbolic protocol analysis
e
in the union of disjoint intruder theories: Combining decision procedures.
Theor. Comput. Sci., 411(10):1261–1282, 2010.
[77] Yannick Chevalier and Laurent Vigneron. A tool for lazy verification of
security protocols. In ASE, pages 373–376. IEEE Computer Society, 2001.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-217-320.jpg)
![218 BIBLIOGRAPHY
[78] Yannick Chevalier and Laurent Vigneron. Towards efficient automated
verification of security protocols. In In Proceedings of the Verification
Workshop (VERIFY’01) (in connection with IJCAR’01), Universit¡E0¿
degli studi di Siena, TR DII 08/01, pages 19–33, 2001.
[79] Yannick Chevalier and Laurent Vigneron. Automated unbounded verifi-
cation of security protocols. In Ed Brinksma and Kim Guldstrand Larsen,
editors, CAV, volume 2404 of Lecture Notes in Computer Science, pages
324–337. Springer, 2002.
[80] Najah Chridi, Mathieu Turuani, and Micha¨l Rusinowitch. Decidable
e
analysis for a class of cryptographic group protocols with unbounded lists.
In CSF [2], pages 277–289.
[81] Erik Christensen, Francisco Curbera, Greg Meredith, and Sanjiva Weer-
awarana. Web services description language (wsdl) 1.1. Available at
http://www.w3.org/TR/wsdl11/, 2001.
[82] Stefan Ciobˆca and V´ronique Cortier. Protocol composition for arbitrary
a e
primitives. In Proceedings of the 23rd IEEE Computer Security Founda-
tions Symposium, CSF 2010, Edinburgh, United Kingdom, July 17-19,
2010, pages 322–336. IEEE Computer Society, 2010.
[83] Michael R. Clarkson and Fred B. Schneider. Hyperproperties. In Datta
[92], pages 51–65.
[84] Hubert Comon-Lundh and V´ronique Cortier. New decidability results for
e
fragments of first-order logic and application to cryptographic protocols.
In Robert Nieuwenhuis, editor, RTA, volume 2706 of Lecture Notes in
Computer Science, pages 148–164. Springer, 2003.
[85] Hubert Comon-Lundh and V´ronique Cortier. Security properties: Two
e
agents are sufficient. In Pierpaolo Degano, editor, ESOP, volume 2618 of
Lecture Notes in Computer Science, pages 99–113. Springer, 2003.
[86] Hubert Comon-Lundh and V´ronique Cortier. Computational soundness
e
of observational equivalence. In ACM Conference on Computer and Com-
munications Security, pages 109–118, 2008.
[87] The World Wide Web Consortium. Simple Object Access Protocol 1.2.
http://www.w3.org/TR/soap12-part1, Apr 2007.
[88] V´ronique Cortier, J´r´mie Delaitre, and St´phanie Delaune. Safely com-
e ee e
posing security protocols. In Vikraman Arvind and Sanjiva Prasad, edi-
tors, FSTTCS, volume 4855 of Lecture Notes in Computer Science, pages
352–363. Springer, 2007.
[89] V´ronique Cortier and St´phanie Delaune. A method for proving obser-
e e
vational equivalence. In Proceedings of the 22nd IEEE Computer Security
Foundations Symposium (CSF’09), pages 266–276. IEEE Computer Soci-
ety Press, 2009.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-218-320.jpg)
![BIBLIOGRAPHY 219
[90] V´ronique Cortier, Micha¨l Rusinowitch, and Eugen Zalinescu. A resolu-
e e
tion strategy for verifying cryptographic protocols with cbc encryption and
blind signatures. In Pedro Barahona and Amy P. Felty, editors, PPDP,
pages 12–22. ACM, 2005.
[91] C.J.F. Cremers. Feasibility of multi-protocol attacks. In Proc. of The First
International Conference on Availability, Reliability and Security (ARES),
pages 287–294, Vienna, Austria, April 2006. IEEE Computer Society.
[92] Anupam Datta, editor. Proceedings of the 21st IEEE Computer Secu-
rity Foundations Symposium, CSF 2008, Pittsburgh, Pennsylvania, 23-25
June 2008. IEEE Computer Society, 2008.
[93] Magnus Daum and Stefan Lucks. Hash collisions (the poisoned
message attack). http://th.informatik.uni-mannheim.de/people/
lucks/HashCollisions/, 2005.
[94] Hans de Nivelle. Chapter 3: Logic Preliminaries. University of Delft,
1996.
[95] Hans de Nivelle. Chapter 4: How to Obtain Resolution Calculi, Section
5, Refinements. University of Delft, 1996.
[96] St´phanie Delaune, Steve Kremer, and Mark Ryan. Verifying privacy-type
e
properties of electronic voting protocols. Journal of Computer Security,
17(4):435–487, 2009.
[97] St´phanie Delaune, Steve Kremer, and Graham Steel. Formal analysis of
e
PKCS#11. In Proceedings of the 21st IEEE Computer Security Founda-
tions Symposium (CSF’08), pages 331–344, Pittsburgh, PA, USA, June
2008. IEEE Computer Society Press.
[98] Grit Denker and Jon Millen. Capsl and cil language design - a common
authentication protocol specification language and its intermediate lan-
guage, 1999.
[99] Grit Denker and Jonathan K. Millen. Modeling group communication
protocols using multiset term rewriting. Electr. Notes Theor. Comput.
Sci., Proceedings of the 2002 Workshop on Rewriting Logic and its Ap-
plications, 71, 2002.
[100] Nachum Dershowitz and Jean-Pierre Jouannaud. Rewrite systems. In
Handbook of Theoretical Computer Science, Volume B: Formal Models
and Sematics (B), pages 243–320. Elsevier and MIT Press, 1990.
[101] Nachum Dershowitz and Ralf Treinen. Rta list of open problems, problem
37. http://rtaloop.mancoosi.univ-paris-diderot.fr/problems/
summary.html, 1998.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-219-320.jpg)
![220 BIBLIOGRAPHY
[102] T. Dierks and C. Allen. The tls protocol version 1.0. Technical Report
RFC 2246, Internet Engineering Task Force (IETF), January 1999.
[103] T. Dierks and E. Rescorla. The transport layer security (tls) protocol
version 1.1. Technical Report RFC 4346, Internet Engineering Task Force
(IETF), April 2006.
[104] Whitfield Diffie and Martin E. Hellman. Multiuser cryptographic tech-
niques. In AFIPS National Computer Conference, volume 45 of AFIPS
Conference Proceedings, pages 109–112. AFIPS Press, 1976.
[105] Yun Ding and Patrick Horster. Undetectable on-line password guessing
attacks. Operating Systems Review, 29(4):77–86, 1995.
[106] D. Dolev and A. Yao. On the Security of Public-Key Protocols. IEEE
Transactions on Information Theory, 2(29), 1983.
[107] Daniel J. Dougherty, Kathi Fisler, and Shriram Krishnamurthi. Specifying
and reasoning about dynamic access-control policies. In of Lecture Notes
in Computer Science, pages 632–646. Springer, 2006.
[108] Gilles Dowek. A unification algorithm for second order linear terms. un-
published manuscript, 1993.
[109] Gilles Dowek. Higher-order unification and matching. In Robinson and
Voronkov [188], pages 1009–1062.
[110] Marwa El Houri. A formal model to express dynamic policies for access
control and trust negotiation in a distributed environment. Th`se de doc-
e
torat, Universit´ Paul Sabatier, Toulouse, France, mai 2010.
e
[111] F. Javier Thayer F´brega, Jonathan C. Herzog, and Joshua D. Guttman.
a
Strand spaces: Proving security protocols correct. Journal of Computer
Security, 7:191–230, 1999.
[112] Christian G. Ferm¨ller, Alexander Leitsch, Ullrich Hustadt, and Tanel
u
Tammet. Resolution decision procedures. In Robinson and Voronkov
[188], pages 1791–1849.
[113] David Ferraiolo and Richard Kuhn. Role-based access control. In In
15th NIST-NCSC National Computer Security Conference, pages 554–
563, 1992.
[114] R. Fielding, J. Gettys, J. Mogul, H. Frystyk, L. Masinter, and T. Berners-
Lee. Hypertext transfer protocol – http/1.1. Technical Report RFC 2616,
Internet Engineering Task Force (IETF), June 1999.
[115] Zvi Galil, Stuart Haber, and Moti Yung. Symmetric public-key encryp-
tion. In Hugh C. Williams, editor, CRYPTO, volume 218 of Lecture Notes
in Computer Science, pages 128–137. Springer, 1985.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-220-320.jpg)
![BIBLIOGRAPHY 221
[116] Taher El Gamal. A public key cryptosystem and a signature scheme based
on discrete logarithms. In CRYPTO, pages 10–18, 1984.
[117] Dimitrios Georgakopoulos, Mark F. Hornick, and Amit P. Sheth. An
overview of workflow management: From process modeling to workflow
automation infrastructure. Distributed and Parallel Databases, 3(2):119–
153, 1995.
[118] Robert Givan and David A. McAllester. New results on local inference
relations. In KR, pages 403–412, 1992.
[119] Shafi Goldwasser and Silvio Micali. Probabilistic encryption and how to
play mental poker keeping secret all partial information. In STOC, pages
365–377. ACM, 1982.
[120] W3C XML Protocol Working Group. Soap version 1.2, part1: Messaging
framework, April 2007.
[121] Yuri Gurevich and Itay Neeman. Dkal: Distributed-knowledge authoriza-
tion language. In CSF ’08: Proceedings of the 2008 21st IEEE Computer
Security Foundations Symposium, pages 149–162, Washington, DC, USA,
2008. IEEE Computer Society.
[122] Sebastian Hinz, Karsten Schmidt 0004, and Christian Stahl. Transforming
bpel to petri nets. In Wil M. P. van der Aalst, Boualem Benatallah, Fabio
Casati, and Francisco Curbera, editors, Business Process Management,
volume 3649, pages 220–235, 2005.
[123] Jieh Hsiang and Micha¨l Rusinowitch. On word problems in equational
e
theories. In Thomas Ottmann, editor, ICALP, volume 267 of Lecture
Notes in Computer Science, pages 54–71. Springer, 1987.
[124] G´rard Huet. Constrained Resolution: A Complete Method for Higher
e
Order Logic. PhD thesis, Case Western Reserve University, 1972.
[125] Hans H¨ttel. Deciding framed bisimilarity. Presented at the INFINITY’02
u
workshop, June 2002.
[126] Florent Jacquemard, Micha¨l Rusinowitch, and Laurent Vigneron. Com-
e
piling and verifying security protocols. In Michel Parigot and Andrei
Voronkov, editors, LPAR, volume 1955 of Lecture Notes in Computer Sci-
ence, pages 131–160. Springer, 2000.
[127] Don Johnson, Alfred Menezes, and Scott Vanstone. The elliptic curve
digital signature algorithm (ecdsa). International Journal of Information
Security, 1:36–63, 2001. 10.1007/s102070100002.
[128] Diane Jordan and John Evdemon et al. Web services business process
execution language version 2.0. Available at http://docs.oasis-open.
org/wsbpel/2.0/OS/wsbpel-v2.0-OS.html, 2007.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-221-320.jpg)
![222 BIBLIOGRAPHY
[129] Anas Abou El Kalam, Salem Benferhat, Alexandre Mi`ge, Rania El Baida,
e
Fr´d´ric Cuppens, Claire Saurel, Philippe Balbiani, Yves Deswarte, and
e e
Gilles Trouessin. Organization based access contro. In POLICY, pages
120–. IEEE Computer Society, 2003.
[130] Deepak Kapur, Paliath Narendran, and Linda Wang. An e-unification
algorithm for analyzing protocols that use modular exponentiation. In
Robert Nieuwenhuis, editor, Rewriting Techniques and Applications, 14th
International Conference, RTA 2003, Valencia, Spain, June 9-11, 2003,
Proceedings, volume 2706 of Lecture Notes in Computer Science, pages
165–179. Springer, 2003.
[131] Nickolas Kavantzas, David Burdett, Gregory Ritzinger, Tony Fletcher,
Yves Lafon, and Charlton Barreto. Web Services Choreography De-
scription Language Version 1.0. Available at http://www.w3.org/TR/
ws-cdl-10/, 2005.
[132] John Kelsey, Bruce Schneier, and David Wagner. Protocol interactions
and the chosen protocol attack. In Proceedings of the 5th Interna-
tional Workshop on Security Protocols, pages 91–104, London, UK, 1998.
Springer-Verlag.
[133] Hristo Koshutanski and Fabio Massacci. An access control framework
for business processes for web services. In Sushil Jajodia and Michiharu
Kudo, editors, XML Security, pages 15–24. ACM, 2003.
[134] Mounira Kourjieh. Logical Analysis and Verification of Cryptographic Pro-
tocols. Th`se de doctorat, Universit´ Paul Sabatier, Toulouse, France,
e e
d´cembre 2009.
e
[135] Robert Kowalski and Patrick J. Hayes. Semantic trees in automated the-
orem proving. Machine Intelligence, 4, 1969.
[136] Steve Kremer, Antoine Mercier, and Ralf Treinen. Reducing equational
theories for the decision of static equivalence. In Anupam Datta, editor,
Proceedings of the 13th Asian Computing Science Conference (ASIAN’09),
volume 5913 of Lecture Notes in Computer Science, pages 94–108, Seoul,
Korea, December 2009. Springer.
[137] Ralf K¨sters and Tomasz Truderung. Using proverif to analyze protocols
u
with diffie-hellman exponentiation. In CSF [2], pages 157–171.
[138] Ralf K¨sters and Max Tuengerthal. Joint state theorems for public-key
u
encryption and digital signature functionalities with local computation.
In Datta [92], pages 270–284.
[139] Ralf K¨sters and Max Tuengerthal. Computational soundness for key
u
exchange protocols with symmetric encryption. In Ehab Al-Shaer, Somesh
Jha, and Angelos D. Keromytis, editors, ACM Conference on Computer
and Communications Security, pages 91–100. ACM, 2009.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-222-320.jpg)
![BIBLIOGRAPHY 223
[140] Ralf K¨sters and Thomas Wilke. Transducer-based analysis of crypto-
u
graphic protocols. Inf. Comput., 205(12):1741–1776, 2007.
[141] D.S. Lankford. Canonical inference. Technical Report Report ATP-32,
University of Texas at Austin, 1975.
[142] Arjen K. Lenstra and Benne de Weger. On the possibility of construct-
ing meaningful hash collisions for public keys. In Colin Boyd and Juan
Manuel Gonz´lez Nieto, editors, ACISP, volume 3574 of Lecture Notes in
a
Computer Science, pages 267–279. Springer, 2005.
[143] Jordi Levy. Linear second-order unification. In Harald Ganzinger, editor,
RTA, volume 1103 of Lecture Notes in Computer Science, pages 332–346.
Springer, 1996.
[144] Zhiyao Liang and Rakesh M. Verma. Correcting and improving the np
proof for cryptographic protocol insecurity. In Atul Prakash and Indranil
Gupta, editors, ICISS, volume 5905 of Lecture Notes in Computer Science,
pages 101–116. Springer, 2009.
[145] Peter A. Loscocco, Stephen D. Smalley, Patrick A. Muckelbauer, Ruth C.
Taylor, S. Jeff Turner, and John F. Farrell. The inevitability of failure:
The flawed assumption of security in modern computing environments. In
In Proceedings of the 21st National Information Systems Security Confer-
ence, pages 303–314, 1998.
[146] Donald W. Loveland. Automated theorem proving : a logical basis. Num-
ber 6 in Fundamental studies in computer science. North-Holland Pub.
Co., Elsevier, 1978.
[147] Gavin Lowe. Breaking and fixing the needham-schroeder public-key pro-
tocol using fdr. In Tiziana Margaria and Bernhard Steffen, editors,
TACAS, volume 1055 of Lecture Notes in Computer Science, pages 147–
166. Springer, 1996.
[148] Gavin Lowe. Casper: A compiler for the analysis of security protocols.
Journal of Computer Security, 6(1-2):53–84, 1998.
[149] Roberto Lucchi and Manuel Mazzara. A pi-calculus based semantics for
ws-bpel. J. Log. Algebr. Program., 70(1):96–118, 2007.
[150] Christopher Lynch. Personnal communication. Toulouse, december 2009,
2009.
[151] Pierre Marchand. Cours de logique de dea. unpublished manuscript, 1986.
[152] Alberto Martelli and Ugo Montanari. Theorem proving with structure
sharing and efficient unification. In IJCAI, page 543, 1977.
[153] S.J. Maslov. An inverse method for establishing deducibility in the clas-
sical predicate calculus. Dokl. Akad. Nau. SSSR, 159:1420–1424, 1964.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-223-320.jpg)
![224 BIBLIOGRAPHY
[154] S.J. Maslov. An inverse method for establishing deducibility for logical
calculi. Trudy Mat. Inst. Steklov, 98:26–87, 1968.
[155] Jay A. McCarthy and Shriram Krishnamurthi. Cryptographic protocol
explication and end-point projection. In Sushil Jajodia and Javier L´pez,
o
editors, Computer Security - ESORICS 2008, 13th European Symposium
on Research in Computer Security, M´laga, Spain, October 6-8, 2008.
a
Proceedings, volume 5283 of Lecture Notes in Computer Science, pages
533–547. Springer, 2008.
[156] Jay A. McCarthy, Shriram Krishnamurthi, Joshua D. Guttman, and
John D. Ramsdell. Compiling cryptographic protocols for deployment
on the web. In Carey L. Williamson, Mary Ellen Zurko, Peter F. Patel-
Schneider, and Prashant J. Shenoy, editors, Proceedings of the 16th Inter-
national Conference on World Wide Web, WWW 2007, Banff, Alberta,
Canada, pages 687–696. ACM, 2007.
[157] Antoine Mercier. Contributions ` l’analyse automatique des protocoles
a
cryptographiques en pr´sence de propri´t´s alg´briques : protocoles de
e ee e
groupe, ´quivalence statique. Th`se de doctorat, Laboratoire Sp´cification
e e e
et V´rification, ENS Cachan, France, December 2009.
e
[158] Ralph C. Merkle. Secure communications over insecure channels. Com-
mun. ACM, 21(4):294–299, 1978.
[159] Middleware and Related Services PTF. Common object request broker
architecture (corba/iiop) v 3.1. Technical report, Object Modeling Group,
January 2008. Available at http://www.omg.org/spec/CORBA/3.1/.
[160] Jonathan K. Millen. A necessarily parallel attack. In In Workshop on
Formal Methods and Security Protocols, 1999.
[161] Jonathan K. Millen and Vitaly Shmatikov. Constraint solving for
bounded-process cryptographic protocol analysis. In ACM Conference
on Computer and Communications Security, pages 166–175, 2001.
[162] Sebastian M¨dersheim. Algebraic properties in alice and bob notation.
o
In Proceedings of the The Forth International Conference on Availability,
Reliability and Security, ARES 2009, March 16-19, 2009, Fukuoka, Japan,
pages 433–440. IEEE Computer Society, 2009.
[163] Sebastian M¨dersheim and Luca Vigan`. Secure pseudonymous channels.
o o
In Michael Backes and Peng Ning, editors, ESORICS, volume 5789 of
Lecture Notes in Computer Science, pages 337–354. Springer, 2009.
[164] S. Narayanan and S. McIlraith. Simulation, verification and automated
composition of web services. In Proceedings of the Eleventh International
World Wide Web Conference (WWW-11), pages 77–88, Honolulu, Hawaii,
USA, May 7-11 2002.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-224-320.jpg)
![BIBLIOGRAPHY 225
[165] NBS. Federal information processing standard (fips) for the data encryp-
tion standard. Technical Report FIPS-46, National Bureau of Standards
(NBS), May 1975.
[166] Roger M. Needham and Michael D. Schroeder. Using encryption for au-
thentication in large networks of computers. Commun. ACM, 21(12):993–
999, 1978.
[167] Robert Nieuwenhuis and Fernando Orejas. Clausal rewriting. In St´phane
e
Kaplan and Mitsuhiro Okada, editors, CTRS, volume 516 of Lecture Notes
in Computer Science, pages 246–258. Springer, 1990.
[168] Robert Nieuwenhuis and Albert Rubio. Ac-superposition with constraints:
No ac-unifiers needed. In Bundy [46], pages 545–559.
[169] NIST. Federal information processing standard (fips) for the data encryp-
tion standard. Technical Report FIPS-46.3, National Institute of Stan-
dards and Technology (NIST), October 1999.
[170] NIST. Federal information processing standard (fips) for the advanced
encryption standard. Technical Report FIPS-197, National Institute of
Standards and Technology (NIST), November 2001.
[171] Oasis Consortium. Web Services Business Process Execution Language
Version 2.0. http://www.oasis-open.org/committees/documents.
php?wg_abbrev=wsbpel, 23 January, 2006.
[172] Oasis Technical Comittee on Secure Exchange. Ws-securitypolicy
1.2. http://doc.oasis-open.org/ws-sx/ws-securitypolicy/200702/
ws-securitypolicy-1.2-spec-cd-02.pdf, 2007.
[173] OASIS XACML TC. Xacml 2.0 core: extensible access con-
trol markup. Available at http://docs.oasis-open.org/xacml/2.0/
access_control-xacml-2.0-core-spec-os.pdf, 2005.
[174] Mitsu Okada and Ichiro Satoh, editors. Advances in Computer Science -
ASIAN 2006. Secure Software and Related Issues, 11th Asian Computing
Science Conference, Tokyo, Japan, December 6-8, 2006, Revised Selected
Papers, volume 4435 of Lecture Notes in Computer Science. Springer,
2008.
[175] Federica Paci, Elisa Bertino, and Jason Crampton. An access-control
framework for ws-bpel. Int. J. Web Service Res., 5(3):20–43, 2008.
[176] Frank Pfenning, editor. Term Rewriting and Applications, 17th Inter-
national Conference, RTA 2006, Seattle, WA, USA, August 12-14, 2006,
Proceedings, volume 4098 of Lecture Notes in Computer Science. Springer,
2006.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-225-320.jpg)
![226 BIBLIOGRAPHY
[177] Birgit Pfitzmann, Matthias Schunter, and Michael Waidner. Crypto-
graphic security of reactive systems. Electr. Notes Theor. Comput. Sci.,
32, 2000.
[178] M. Pistore, A. Marconi, P. Bertoli, and P. Traverso. Automated compo-
sition of Web Services by Planning at the knowledge Level. In Proc. Int.
Joint Conf. on Artificiel Intelligence, IJCAI 2005, pages 1252–1259, 2005.
[179] PKCS Editor. Pkcs #1 v1.5: Rsa cryptography standard. Technical
Report PKCS #1, RSA Laboratories, 1993.
[180] PKCS Editor. Pkcs #1 v2.1: Rsa cryptography standard. Technical Re-
port PKCS #1, RSA Laboratories, 2002. OAEP description in Section 7.1.
[181] Gordon D. Plotkin. Building-in equational theories. Machine Intelligence,
7:73–90, 1972. also available at http://homepages.inf.ed.ac.uk/gdp/
publications/building_in_equational_theories.pdf.
[182] J. M. Pollard. A monte carlo method for factorization. Nordisk Tidskrift
for Informationsbehandlung (BIT), 15:331–334, 1975.
[183] W. V. Quine. A proof procedure for quantification theory. Journal of
Symbolic Logic, 20:141–149, June 1955.
[184] Charles Rackoff and Daniel R. Simon. Non-interactive zero-knowledge
proof of knowledge and chosen ciphertext attack. In Joan Feigenbaum,
editor, CRYPTO, volume 576 of Lecture Notes in Computer Science, pages
433–444. Springer, 1991.
[185] Ramaswamy Ramanujam and S. P. Suresh. Tagging makes secrecy decid-
able with unbounded nonces as well. In Paritosh K. Pandya and Jaikumar
Radhakrishnan, editors, FSTTCS, volume 2914 of Lecture Notes in Com-
puter Science, pages 363–374. Springer, 2003.
[186] Ronald L. Rivest, Adi Shamir, and Leonard M. Adleman. A method
for obtaining digital signatures and public-key cryptosystems. Commun.
ACM, 21(2):120–126, 1978.
[187] Roberto Chinnici and Jean-Jacques Moreau and Arthur Ryman and San-
jiva Weerawarana. Web Services Description Language (WSDL) 2.0.
http://www.w3.org/TR/wsdl20/, June 2007.
[188] John Alan Robinson and Andrei Voronkov, editors. Handbook of Auto-
mated Reasoning (in 2 volumes). Elsevier and MIT Press, 2001.
[189] Michael Rusinowitch. D´monstration automatique:
e techniques de
r´´criture. InterEditions, 1989.
ee
[190] Micha¨l Rusinowitch and Mathieu Turuani. Protocol insecurity with finite
e
number of sessions is NP-complete. In CSFW [1], pages 174–.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-226-320.jpg)
![BIBLIOGRAPHY 227
[191] Manfred Schmidt-Schauß. Unification in a combination of arbitrary dis-
joint equational theories. In Claude Kirchner, editor, Unification, pages
217–265. Academic Press, 1986.
[192] Bruce Schneier. Applied cryptography. Addison-Wesley, 1996.
[193] Klaus U. Schulz. Makanin’s algorithm for word equations - two improve-
ments and a generalization. In Klaus U. Schulz, editor, IWWERT, volume
572 of Lecture Notes in Computer Science, pages 85–150. Springer, 1990.
[194] Helmut Seidl and Kumar Neeraj Verma. Flat and one-variable clauses:
Complexity of verifying cryptographic protocols with single blind copying.
In Franz Baader and Andrei Voronkov, editors, LPAR, volume 3452 of
Lecture Notes in Computer Science, pages 79–94. Springer, 2004.
[195] Helmut Seidl and Kumar Neeraj Verma. Flat and one-variable clauses:
Complexity of verifying cryptographic protocols with single blind copying.
ACM Trans. Comput. Log., 9(4), 2008.
[196] Helmut Seidl and Kumar Neeraj Verma. Flat and one-variable clauses
for single blind copying protocols: The xor case. In Ralf Treinen, editor,
RTA, volume 5595 of Lecture Notes in Computer Science, pages 118–132.
Springer, 2009.
[197] Victor Shoup, editor. Advances in Cryptology - CRYPTO 2005: 25th
Annual International Cryptology Conference, Santa Barbara, California,
USA, August 14-18, 2005, Proceedings, volume 3621 of Lecture Notes in
Computer Science. Springer, 2005.
[198] Thoralf Skolem. Logisch-kombinatorische untersuchungen uber die
¨
erf¨llbarkeit oder beweisbarkeit mathematischer s¨tze nebst einem the-
u a
oreme uber dichte mengen. Skrifter utgit av Videnskapsselskapet i Kris-
¨
tiani, I. Matematisk-naturvidenskabelig klasse, 4:1–36, 1920.
[199] Marc Stevens, Arjen K. Lenstra, and Benne de Weger. Chosen-prefix
collisions for md5 and colliding x.509 certificates for different identities.
In Moni Naor, editor, EUROCRYPT, volume 4515 of Lecture Notes in
Computer Science, pages 1–22. Springer, 2007.
[200] Scott D. Stoller. A reduction for automated verification of authentica-
tion protocols. Technical Report 520, Computer Science Dept., Indiana
University, December 1998.
[201] Scott D. Stoller. A reduction for automated analysis of authentication pro-
tocols. In Workshop on Formal Methods and Security Protocols, July 1999.
Also appeared as Indiana University, Computer Science Dept., Technical
Report 520, Dec. 1998.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-227-320.jpg)
![228 BIBLIOGRAPHY
[202] The Avantssar Project. Problem cases and their trust and security re-
quirements. Deliverable D5.1, Automated VAlidatioN of Trust and Se-
curity of Service-oriented ARchitectures (AVANTSSAR), http://www.
avantssar.eu/, 2008.
[203] The World Wide Web Consortium. XML Schema Definition (XSD). http:
//www.w3.org/XML/Schema, March 2005.
[204] Erik Tid´n. Unification in combinations of collapse-free theories with
e
disjoint sets of function symbols. In J¨rg H. Siekmann, editor, 8th Inter-
o
national Conference on Automated Deduction, Oxford, England, July 27
- August 1, 1986, Proceedings, volume 230 of Lecture Notes in Computer
Science, pages 431–449. Springer, 1986.
[205] Yoshihito Toyama. Counterexamples to termination for the direct sum of
term rewriting systems. Inf. Process. Lett., 25(3):141–143, 1987.
[206] Tomasz Truderung. Regular protocols and attacks with regular knowledge.
In Robert Nieuwenhuis, editor, CADE, volume 3632 of Lecture Notes in
Computer Science, pages 377–391. Springer, 2005.
[207] Max Tuengerthal, Ralf K¨sters, and Mathieu Turuani. Implement-
u
ing a unification algorithm for protocol analysis with xor. CoRR,
abs/cs/0610014, 2006.
[208] Mathieu Turuani. The cl-atse protocol analyser. In Pfenning [176], pages
277–286.
[209] Laurent Vigneron. Associative-commutative deduction with constraints.
In Bundy [46], pages 530–544.
[210] Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu. Finding collisions in the
full sha-1. In Shoup [197], pages 17–36.
[211] Xiaoyun Wang and Hongbo Yu. How to break md5 and other hash func-
tions. In Ronald Cramer, editor, EUROCRYPT, volume 3494 of Lecture
Notes in Computer Science, pages 19–35. Springer, 2005.
[212] Xiaoyun Wang, Hongbo Yu, and Yiqun Lisa Yin. Efficient collision search
attacks on sha-0. In Shoup [197], pages 1–16.
[213] Stephen A. White and Derek Miers. BPMN Modeling and Reference
Guide. Future Strategies Inc, 2008.
[214] Wikipedia. The enigma machine. Available at http://en.wikipedia.
org/wiki/Enigma_machine, 2010.
[215] World Wide Web Consortium. XML Path Language (XPath) 2.0. http:
//www.w3.org/TR/xpath20/, 23 January, 2007.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-228-320.jpg)
![BIBLIOGRAPHY 229
[216] L. Wos and G. Robinson. Paramodulation and set of support. In Sympo-
sium of the INRIA Symposium on Automatic Demonstration, volume 125
of Lecture Notes in Computer Science, pages 276–310. Springer, 1970.
[217] Larry Wos. Automated reasoning: 33 BASIC research problems. Prentice-
Hall, Inc., Upper Saddle River, NJ, USA, 1988.](https://image.slidesharecdn.com/habilitation-110222100401-phpapp02/85/Habilitation-draft-229-320.jpg)