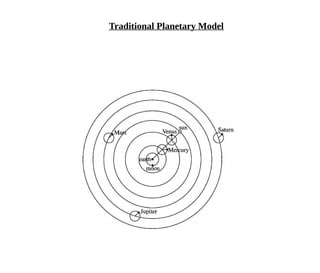
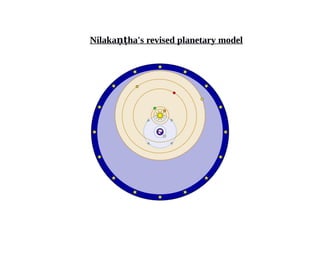
Indian astronomy has a long history dating back to the Vedanga-jyotisha text from 1400 BCE. Key developments include Aryabhata's theory of Earth's rotation in 499 CE and Bhaskara II's non-circular planetary orbits in the 12th century. Indian astronomers made many advances in mathematics needed for accurate astronomical computations, including early work on trigonometric functions and the value of pi. Their models incorporated epicycles and were later revised by Nilakantha Somayaji in the 15th century to resemble a rudimentary heliocentric system.

1. An Overview of Mathematics and Astronomy in India
Venketeswara Pai R.

2.  The word “astronomy” owes its etymology to the Middle English and the Old French term “astronomie” , which, in turn,
was derived from the Latin form “astronomia” through the Greek word “astronomos” meaning 'star-law.'
 In Indian context, astronomy is known popularly by the term जययततशशस/Jyotiśāstra which means Science of
illuminating objects.
 The earliest text on Astronomy is Vedā ga-jyoti aṅ ṣ (1400 BCE). It is a collection of two smaller texts having 35 and 43
verses respectively.
 Simple calculations pertaining to Calendars.
 Therefore, it is also known as Kālavidhānaśāstra.
 Astronomical computations enunciated in Vedā gajyoti aṅ ṣ continued to be in use for a long time
 From the time of Āryabha a (499 AD), there was emerging a new class of astronomical literature called theṭ Siddhāntas.
 A huge corpus of literature available from the time of Āryabha a toṭ Sāmanta Chandraśekhara (18th
Century CE).

3. Prof. David E Pingree (1933 - 2005), Brown University observers:
(REF: David E Pingree, A History of Indian Literature: Jyotiśāstra: Astral and Mathematical Literature, p. 118.)

4. Indian Tradition West Asia Europe
DARK PERIOD
Vararuci (c.350)
Āryabha a (499 CE))ṭ
Varāhamihira (550)
Brahmagupta (628)
Bhāskara I (630)
Current Sūryasiddhānta
Lalla
Va eṭ śvara (906)
Muñjāla (930)
Śrīpati (1050)
Bhāskara II (1150)
Al Fazari (770)
Al Khwarizmi (830)
Thabit ibn Qurra (875)
Al Battani (900)
Al Haytham (1000)
Al Biruni (1030)
Ptolemy (150 CE)
Pappus (320), Theon (370)
Simplicius (530)
Gerard of Cremona (1175)
Mādhava (1380)
Parameśvara (1430)
Nīlaka ha (1500)ṇṭ
Jye hadeva (1530)ṣṭ
Acyuta (1575)
Al Urdi , Al Tusi (1250)
Al Shirazi (1300)
Al Shatir (1375)
Al Kashi (1420) Copernicus (1543)
Tycho Brahe (1587)
Kepler (1609)

6.  The procedure for calculating the geo-centric longitudes of the five
planets, Mercury, Venus, Mars, Jupiter and Saturn involves essentially
the following steps. First, the mean longitude (called the madhyama-
graha) is calculated for the desired day.
 Then two corrections namely the manda-sa skṃ āra and śīghra-
sa skṃ āra are to be applied to the mean planet. The madhyama-graha
corresponds to the mean-heliocentric planet. The manda-correction
corresponds to the equation of centre giving the true heliocentric planet.
The śīghra-sa skṃ āra corresponds to the process of conversion of the
heliocentric longitude to the geocentric longitude.
 In the case of Mercury and Venus, the mean Sun is taken as the mean
planet and the equation of centre is applied to it - a feature common to
all the ancient planetary theories (Indian, Greco-European & Islamic).

7. The manda-correction is given by a variable epicycle model.
Rsin (P‐M) = (r/K) Rsin (M‐U) = (r0/R) Rsin (M‐U)

8. makhi bhakhi phakhi
dhakhi ṇakhi ñakhi
'nakhi hasjha skaki
ki.sga ghakhi kighva |
ghlaki kigra hakya
dhaki kica sga 'sjha
.nva kla pta pha cha
kala-ardha- jy–ah. ||

9. Indian Trignometric function = Jyā = Rsine,
Accuracy of the planetary
longitudes depends on the
accuracies of Rsine which
depends on the accurate
value of Radius, R and
hence pi.
Hence, later astronomers started focussing on developing the Mathematical
techniques for finding accurate trignometric functions and value pi.

14. Bhāskara explains that the epicycle radius in the Manda-process is not
constant. The radius (r) and the hypotenuse (K) both vary in such a way
that their ratio is constant and equal to the ratio of the mean epicycle
radius (r0) and the radius of the concentric circle (R).
This entails that the actual orbit of the planet may be seen to be an oval −
the first non-circular orbit in the history of astronomy.
Bhāskara gives a process of iteration (asak t-karmaṛ ) to calculate r and K.
could easily derive the following formula for the viparīta-kar aṇ

16. Other Contributions
Rotation of the Earth
Till the time of Aryabhata, it was believed that Earth was stationary and all the
planets including celestial sphere was revolving around the Earth.
Aryabhata’s theory of Earth’s rotation.

17. Objections to Aryabhata's theory of Earth's Rotation: Lalla (720 - 790 AD)
If the Earth rotates how could birds in flight return to their nests. (By the time they return, trees on
which the nests were would have sped away)

18. Lalla's Objection continues ......
Arrows thrown vertically upwards would fall towards the west and the clouds would
always be moving to the west.

19. Lalla's Objection continues ......
If it is argued that the earth is moving at a slow speed, how could it then go around
the universe in a day.

20. ● The Earth is supported by a tortoise, a serpent, a boar, elephants or by
mountain ranges, etc.
● All these views are based upon the premise – heavy objects cannot stand in
space without a support

21. Lalla on Situation of Earth
View of Bhaskara II (1114 CE)

22. Traditional Planetary Model

23. Nilaka ha's revised planetary modelṇṭ

24. Source Works
1. Almagest of Claudius Ptolemy, Tr. by G. J. Toomer, Duckworth, London
1984.
2. Āryabhañīya of Āryabhaña (c.499): Ed. with Tr. by K.S.Shukla and
K.V.Sarma, INSA, New Delhi 1976.
3. Āryabhañīyabhāùya of Bhāskarācārya-I (c.630): Ed. By K. S. Shukla,
INSA, New Delhi 1976. Eng Tr. of Gaõitapāda by Agathe Keller, 2
Vols., Basel 2006.
4. Āryabhañīyabhāùya (c.1502) of Nīlakaõñha Somayājī on Āryabhañīya
of Āryabhaña: Ed. by K. Sambasiva Sastri, 3 Vols., Trivandrum 1931,
1932, 1957.
5. Brāhmasphuñasiddhānta and Dhyānagrahopadeśādhyāya of
Brahmagupta, Ed. by Sudhākara Dvivedin, Medical Hall Press, Benares
1902. Brāhmasphuñasiddhānta (c.628) of Brahmagupta: Ed. with
Vāsanā (c.860) of Pçthūdakasvāmin by Ram Swarup Sharma, 4 Vols,
New Delhi 1966. Chapter XXI Ed. with Eng. Tr. by S. Ikeyama, Ind.
Jour History of Sc., 2003
6. Gaõita-yuktibhāùā of Jyeùñhadeva, Ed. and Tr. with Notes by

25. K. V. Sarma, K. Ramasubramanian, M. D. Srinivas and M. S. Sriram,
2 Volumes, Hindustan Book Agency, Delhi 2008 (Rep. Springer, New
York 2009).
7. Laghumānasa of Muñjāla (c.930): Ed. with Tr. and Notes by
K. S. Shukla, INSA New Delhi, 1990.
8. Mahābhāskarīya of Bhāskarācārya-I (c.630): Ed. with commentary of
Govindasvāmin (c.800) and Siddhāntadīpikā of Parameśvara (c.1430)
by T. S. Kuppanna Sastri, Madras 1957. Ed. and Tr with Notes by
K. S. Shukla, Lucknow, 1960.
9. Siddhāntaśiromaõi of Bhāskarācārya II (c. 1150): Ed., with Bhāskara’s
Vāsanā and Nçsiüha Daivajña’s Vāsanāvārttika, by Muralidhara
Chaturveda, Varanasi 1981. Grahagaõitādhyāya Tr. by D. Arka
Somayaji, Kendriya Sanskrit Vidyapeetha, Tirupati 1980.
10. Tantrasaïgraha of Nīlakaõñha Somayājī, Ed. and Tr. with Notes by
K. Ramasubramanian and M. S. Sriram, Springer, New York 2011.
Secondary Works

26. 1. S. B. Dikshit, Bharatiya Jyotish Sastra, (Marathi Edn) Pune 1896. Eng
Tr. by R. V. Vaidya, Delhi 1969.
2. J. Evans, The History and Practice of Ancient Astronomy, Oxford 1998.
3. O. Neugebauer, A History of Ancient Mathematical Astronomy, 3 Vols.,
Springer, New York 1975.
4. D. Pingree, History of Mathematical Astronomy in India, in C. C.
Gillispie Ed., Dictionary of Scientific Biography, Vol XV, New York
1978, p. 533-633.
5. K. Ramasubramanian, M. D. Srinivas and M. S. Sriram, Modification of
the Earlier Indian Planetary Theory by the Kerala Astronomers (c. 1500)
and the implied Heliocentric Picture of Planetary Motion, Current
Science 66, 784-790, 1994.
6. S. Balachandra Rao, Indian Astronomy: An Introduction, Hyderabad
2000.
7. G. Saliba, A History of Arabic Astronomy: Planetary Theory during the
Golden Age of Islam, New York 1994.
8. S N Sen and K. S.Shukla (eds.), A History of Indian Astronomy, INSA
New Delhi 1985, Rev. Edn. 2000.

27. 9. M. D. Srinivas, On the Nature of Mathematics and Scientific
Knowledge in Indian Tradition, in J. M. Kanjirakkat Ed., Science and
Narratives of Nature, Routledge, New York 2015, pp.220-238.
10. M. S. Sriram, K. Ramasubramanian &
M. D. Srinivas, Eds.
500 Years of Tantrasaïgraha: A Landmark in the History of
Astronomy, IIAS, Shimla 2002.
11. M. S. Sriram, Planetary and Lunar Models in Tantrasaïgraha
(c.1500) and Ganitayuktibhasa (c.1530), in C. S. Seshadri (ed.), Studies
in the History of Indian Mathematics, Hindustan Book Agency, Delhi
2010, 353-389.
12. B. V. Subbarayappa, The Tradition of Astronomy in India:
Jyotiþśāstra, PHISPC Vol IV, Part 4, Centre for Studies in Civilizations,
New Delhi 2008
13. N. M. Sverdlow & O. Neugebauer, Mathematical Astronomy in
Copernicus’de Revolutionibus, Springer, New York 1984.