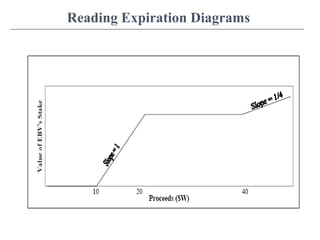
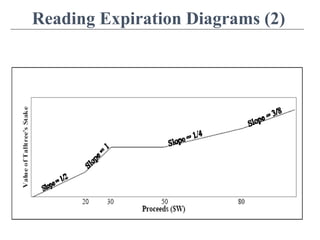
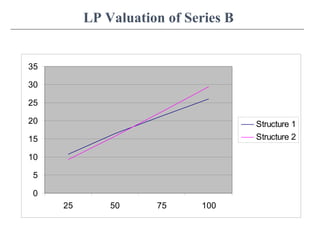
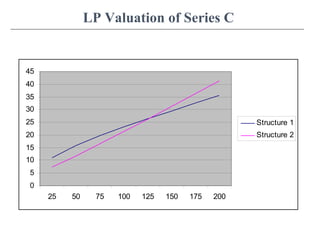
This document discusses partial valuations related to option pricing, preferred stock, and later series investments. It begins by defining options and differentiating between call and put options. It then covers the Black-Scholes option pricing model and its assumptions. Next, it compares the valuation of redeemable and convertible preferred stock, discussing liquidation preferences and breakeven valuations. Finally, it examines later round investments such as Series B, C, and beyond, providing examples of how preferred stock is structured and valued across multiple investment rounds.

1. PARTIAL VALUATION I:PARTIAL VALUATION I:
OPTION PRICING,OPTION PRICING,
PREFERRED STOCK &PREFERRED STOCK &
LATER SERIESLATER SERIES
Prof.Stephen OngProf.Stephen Ong
BSc(Hons)Econs (LSE), MBA (Bradford)BSc(Hons)Econs (LSE), MBA (Bradford)
Visiting Professor, Shenzhen UniversityVisiting Professor, Shenzhen University
Academic Fellow, Entrepreneurship & Innovation,Academic Fellow, Entrepreneurship & Innovation,
The Lord Ashcroft International Business School,The Lord Ashcroft International Business School,
Anglia Ruskin University Cambridge UKAnglia Ruskin University Cambridge UK
MSC TECHNOPRENEURSHIP :MSC TECHNOPRENEURSHIP :
VENTURE CAPITAL FINANCINGVENTURE CAPITAL FINANCING

2. Today’s OverviewToday’s Overview

3. LEARNING OBJECTIVESLEARNING OBJECTIVES
To understand the different methodsTo understand the different methods
of pricing options;of pricing options;
To compare the valuation ofTo compare the valuation of
Redeemable and ConvertibleRedeemable and Convertible
Preferred stock;Preferred stock;
To discuss later round investmentsTo discuss later round investments
such as Series B, C and beyond.such as Series B, C and beyond.

4. 1.Option Pricing

5. Option Definitions
 A European call option gives the holder the right to
buy an asset at a preset exercise price on an
expiration date.
 For a put option, just substitute “sell” for “buy”.
 “Strike price” is a synonym for exercise price.
 For an American option, exercise can occur anytime
on or before the expiration date.

6. Option “Moneyness”
If the exercise price is higher, the same, or lower
than the current stock price, then we say that a call
option is “out-of-the-money”, “at-the-money”, or
“in-the-money”, respectively.
For put options, reverse this ordering (e.g., put
options are out-of-the-money when the exercise
price is lower than the current stock price.)

7. Call Option
X=100
CT(X;T) = Max(VT – X, 0) = C1(100;1) = Max(V1-100,0)

8. Put Option
PT(X;T) = Max(X –VT, 0) = C1(100;1) = Max(100 –V1,0)

9. ExampleExample
Suppose that Bigco is currently trading for $100Suppose that Bigco is currently trading for $100
per share. We are offered a European call optionper share. We are offered a European call option
to purchase one share with an expiration date into purchase one share with an expiration date in
one year. We know that on the expiration dateone year. We know that on the expiration date
Bigco stock will sell for either $120 per share (aBigco stock will sell for either $120 per share (a
“good day”:“good day”: probability = 80%probability = 80%) or for $80 per) or for $80 per
share (a “bad day”:share (a “bad day”: probability = 20%probability = 20%). No other). No other
prices are possible. The stock will not pay anyprices are possible. The stock will not pay any
dividends during the year. The riskless interestdividends during the year. The riskless interest
rate is zero, so a bond can be purchased (or sold)rate is zero, so a bond can be purchased (or sold)
for a face value of $100 and have a certain payofffor a face value of $100 and have a certain payoff
of $100 in one year. Stocks, bonds, and optionsof $100 in one year. Stocks, bonds, and options
can all be bought or sold, long and short, withoutcan all be bought or sold, long and short, without
any transactions costs.any transactions costs.

10. Black-Scholes Assumptions
 “Perfect Markets” that are
Open all the time
Allow assets to be traded in any quantity
No taxes or transactions costs
No remaining arbitrage opportunities
 Technical assumptions about the statistical properties
of stock and bond returns. (Most famously, log
normal stock returns).

11. Black-Scholes FormulaBlack-Scholes Formula
1 2( ) ( )rT
c SN d Xe N d−
= −
2
1
2
2 1
ln( / ) ( / 2)
ln( / ) ( / 2)
S X r T
d
T
S X r T
d d T
T
σ
σ
σ
σ
σ
+ +
=
+ −
= = −
where
S = current stock (or “underlying asset” price
X = Exercise (or “strike”) price
T = Time to expiration (in years)
R = annualized riskfree rate (continuously compounded = log)
σ = volatility (annualized standard deviation of log returns)
N(d) = cumulative normal distribution evaluated at d

12. EXHIBIT 13.7 – FIVE-YEAR COMPOUND
RETURNS FOR A LOGNORMAL DISTRIBUTION

13. Random-Expiration (RE) Options
 Continuous-time probability (q) of forced expiration.
 Expected holding period = H = 1/q
Figure 9.8
T
Probabilityoptionisstillalive
1 2 3 4
.25
.5
.75
1

14. RE Call Formula
1 2
0
[ ( ) ( )]rT qT
SN d Xe N d qe dT
∞
− −
−∫
You do not need to memorize this!You do not need to memorize this!

15. 2.The Valuation of
Preferred Stock

16. Reading Expiration Diagrams

17. Reading Expiration Diagrams (2)

18. Base-Case Option Pricing Assumptions
Riskless interest rate = r = 5%
Expected holding period = H =
5 years for Series A
4 Years for Series B
3 Years for Series C and beyond
Volatility = 90% (from Cochrane, 2005)

19. Some old and new terms
Aggregate Purchase Price (APP): not always the
same as $investment – because of multiple
securities.
Redemption Value (RV): not always the same as
APP – because of liquidation preferences and
dividends.
LP valuation equation
Breakeven valuation

20. Example 1Example 1
EBV considering $6M Series A investment in
Newco
RP ($5M APP) + 5M shares of Common
Pre-money shares = 10M
Question: What is the breakeven valuation?

21. Example 2Example 2
EBV considering $6M Series A investment in
Newco
RP ($5M APP) + 5M shares of Common
2X Liquidation preference
Pre-money shares = 10M
Question: What is the breakeven valuation?

22. Example 3Example 3
EBV considering $6M Series A investment in
Newco
RP ($5M APP) + 5M shares of Common
1% monthly cumulative (simple) dividend
Pre-money shares = 10M
Question: What is the breakeven valuation?

23. Example 4Example 4
EBV considering $6M Series A investment in
Newco
5M shares of CP ($6M APP)
Pre-money shares = 10M
Question: What is the breakeven valuation?

24. Example 5Example 5
EBV considering $12M Series A investment in
Newco
RP ($4M APP) + 5M shares of CP ($6M APP)
Pre-money shares = 10M
Question: What is the breakeven valuation?

25. Example 6Example 6
 EBV considering $6M Series A investment in Newco
 Assume total valuation = $25M
 Two possible structures
RP ($5M APP) + 5M shares of common, or
Z shares of CP ($6M APP)
 Pre-money shares = 10M
 Question: For what number of shares Z should EBV
be indifferent between the structures?

26. 3.Later Round Investments

27. Example 1Example 1
Talltree considering $12M Series B investment in
Newco
Two possible structures
RP ($10M APP and 2X liquidation preference) + 5M
shares of common, or
10M shares of CP ($12M APP)
Employee shares = 10M
Series A investors, EBV, have 10M shares of CP
($6M APP)

28. LP Valuation of Series B
0
5
10
15
20
25
30
35
25 50 75 100
Structure 1
Structure 2

29. Conversion-Order Shortcut
Compute the redemption value per share (RVPS)
for each CP investor
Rank investors by RVPS, lowest to highest
Done

30. Example 2Example 2
 Same setup as Example 1
 Assume Talltree chose the CP structure (no anti-
dilution protection)
 Now, one year later and Owl is considering a $10M
Series C investment in Newco
 Two possible structures
RP ($8M APP and 3X liquidation preference) + 5M shares
of common, or
10M shares of CP ($10M APP)

31. LP Valuation of Series C
0
5
10
15
20
25
30
35
40
45
25 50 75 100 125 150 175 200
Structure 1
Structure 2

32. Example 3Example 3
 All CP Investors, all have 20% carry and a committed capital /All CP Investors, all have 20% carry and a committed capital /
investment capital ratio of 1.25 except for Owl.investment capital ratio of 1.25 except for Owl.
 Series A: $6M for 10M sharesSeries A: $6M for 10M shares (EBV)(EBV)
 Series B: $12M for 10M sharesSeries B: $12M for 10M shares (Talltree)(Talltree)
 Series C: $10M for 10M sharesSeries C: $10M for 10M shares (Owl)(Owl)
 Series D: $10M for 10M shares (2X liq pref)Series D: $10M for 10M shares (2X liq pref) (Series D investors)(Series D investors)
 Series E: $10M for 10M shares (3X liq pref)Series E: $10M for 10M shares (3X liq pref) (Series E investors)(Series E investors)
 Series F: $25M for 10M sharesSeries F: $25M for 10M shares (Series F investors)(Series F investors)

33. Further ReadingFurther Reading
 Metrick, Andrew and Yasuda, Ayako (2011) Venture
Capital & the Finance of Innovation. 2nd
Edition. John
Wiley & Sons.
 Lerner,Losh, Hardymon, Felda and Leamon, Ann
(2012). Venture Capital and Private Equity : A
Casebook. 5th
Edition. John Wiley & Sons.
 Dorf, R.C. and Byers, T.H. (2008) Technology
Ventures – From Idea to Enterprise 2nd
Edition,
McGraw Hill

34. QUESTIONS?