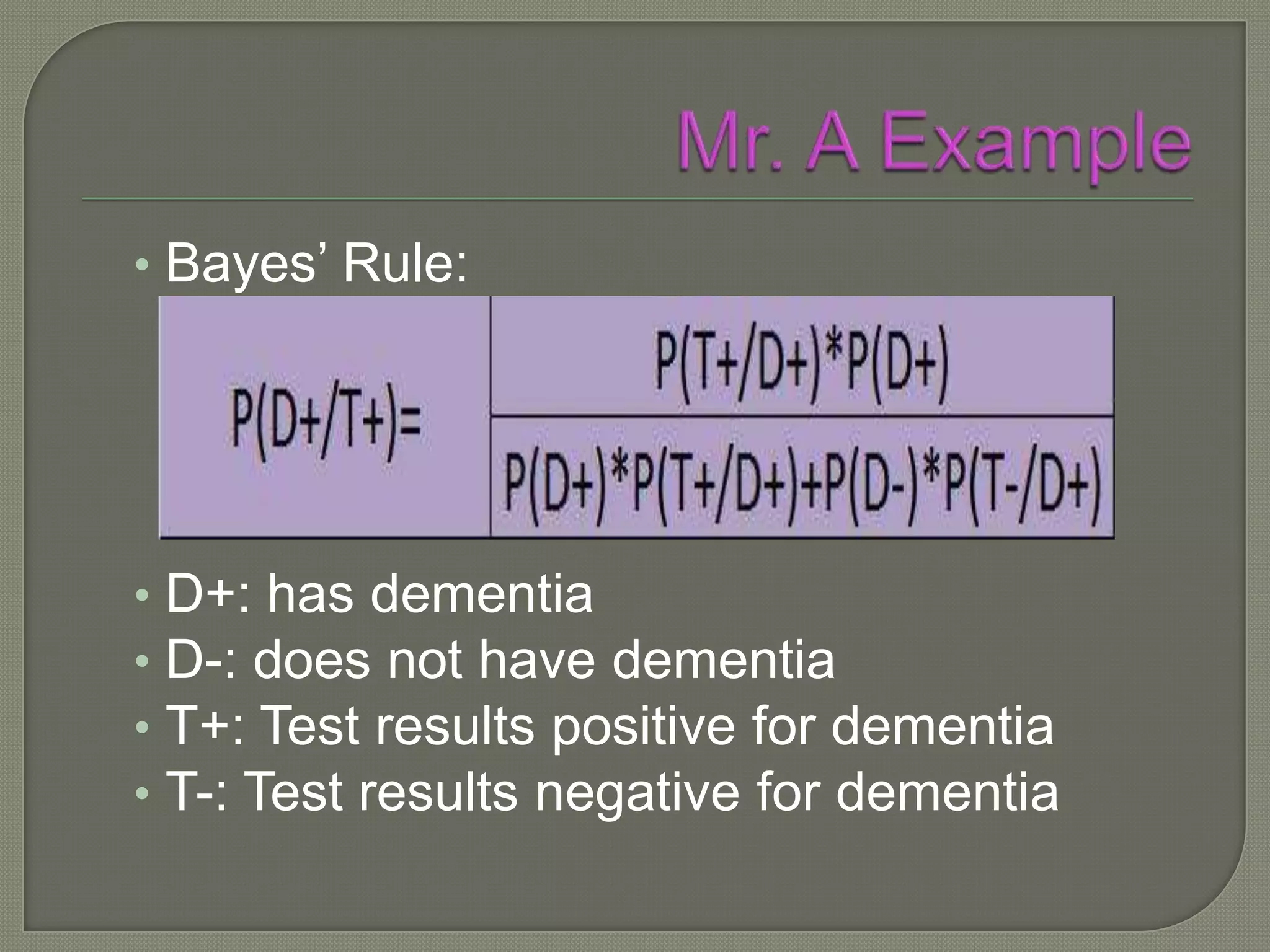
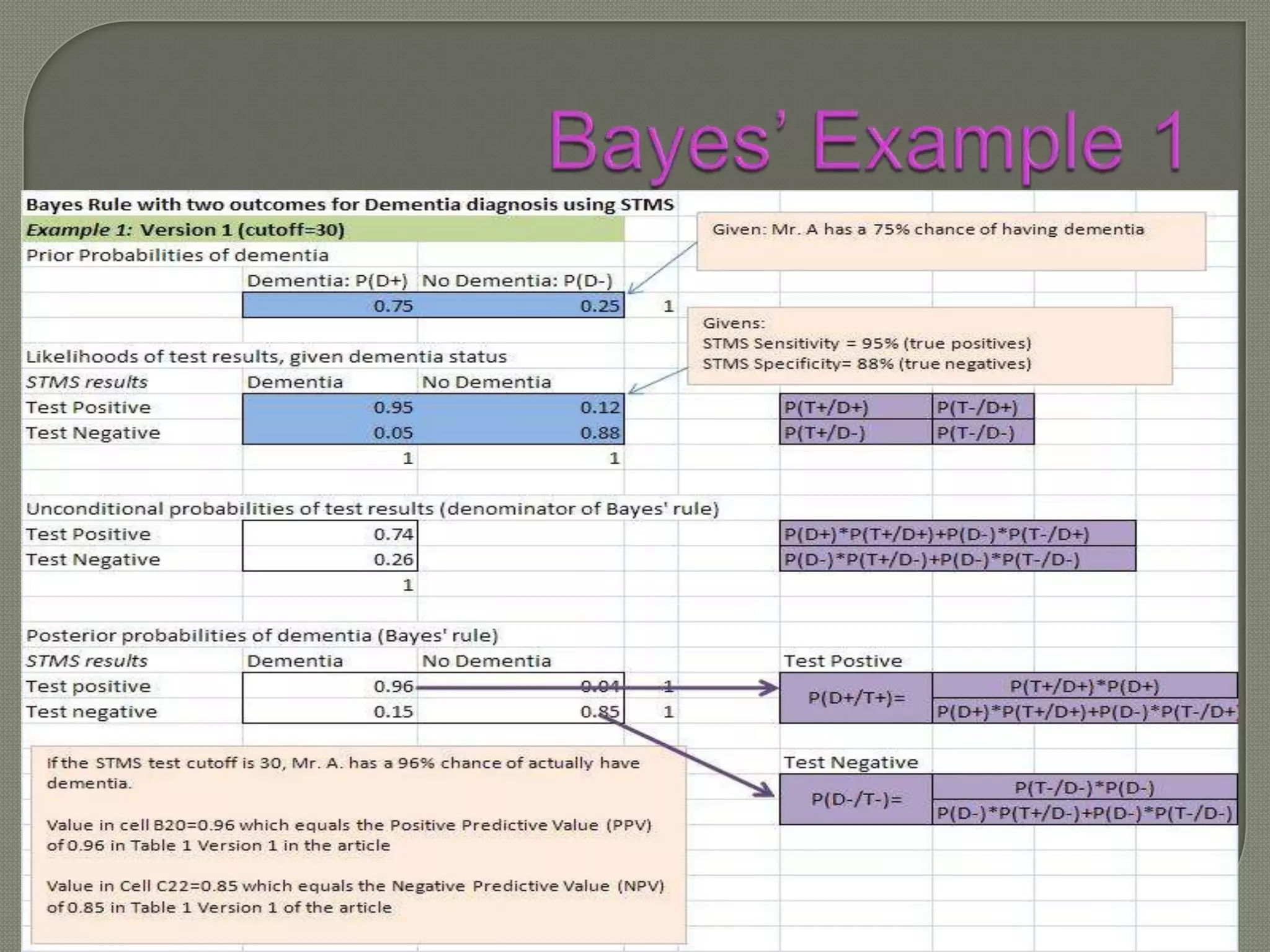
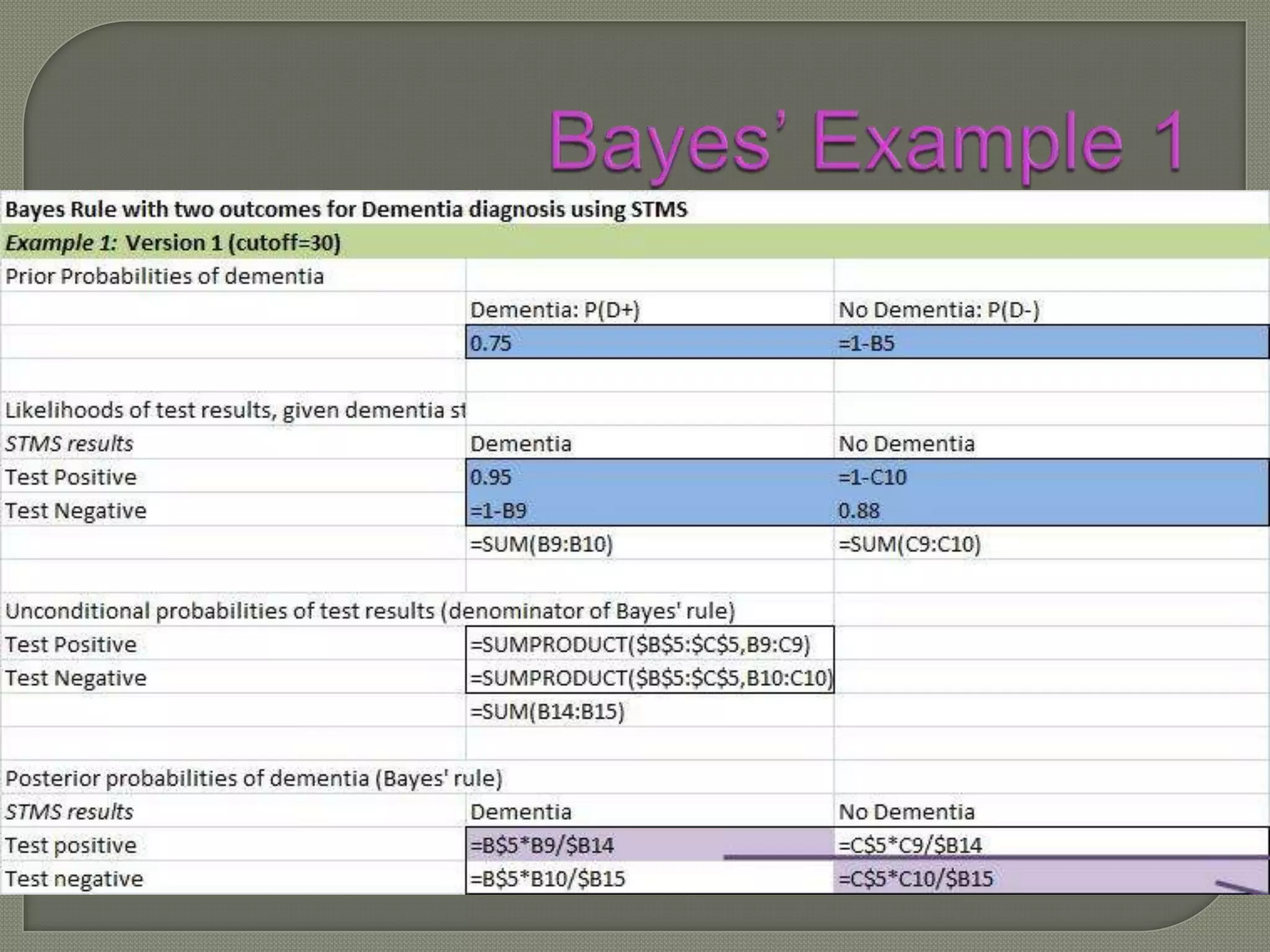
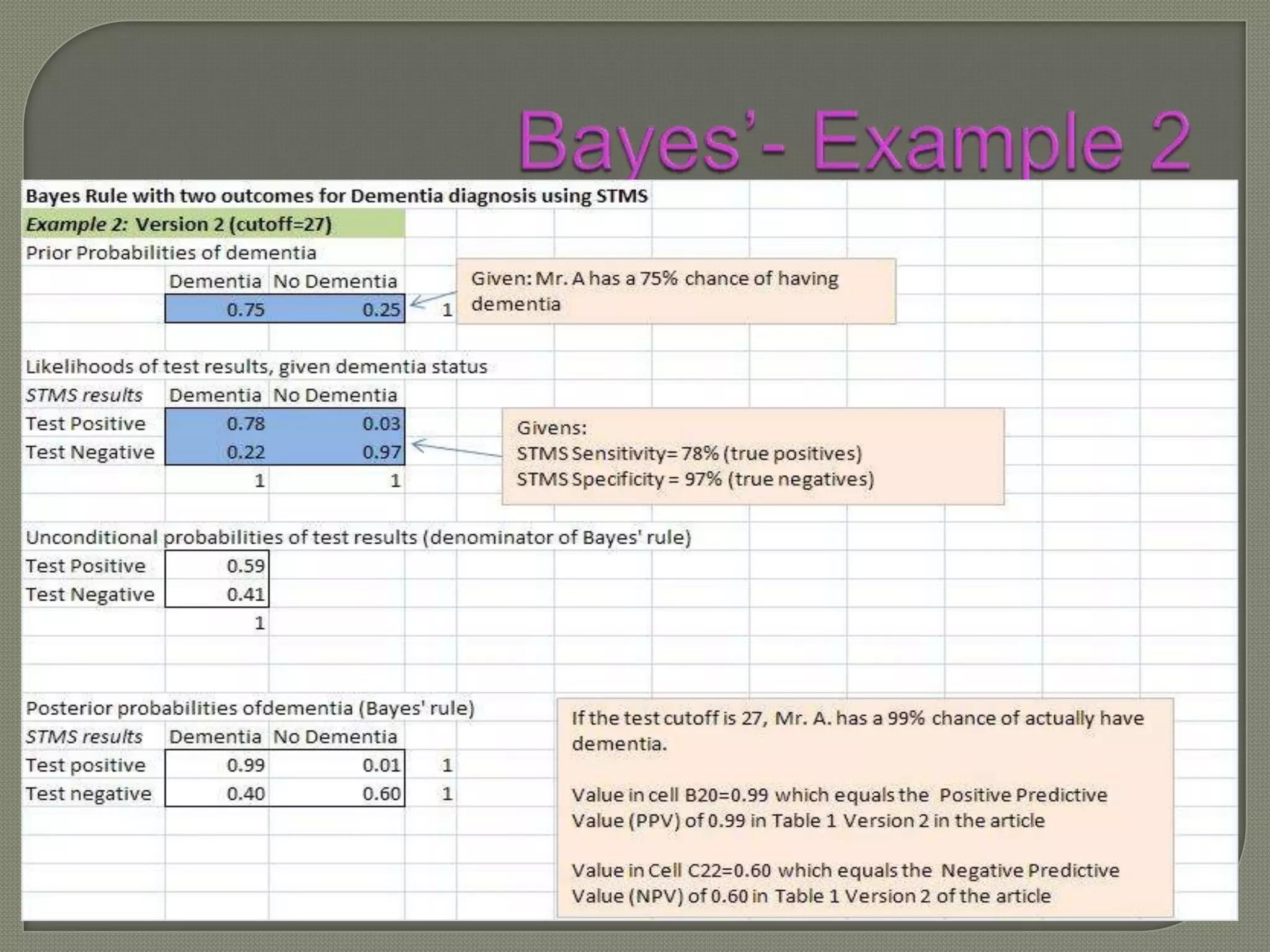
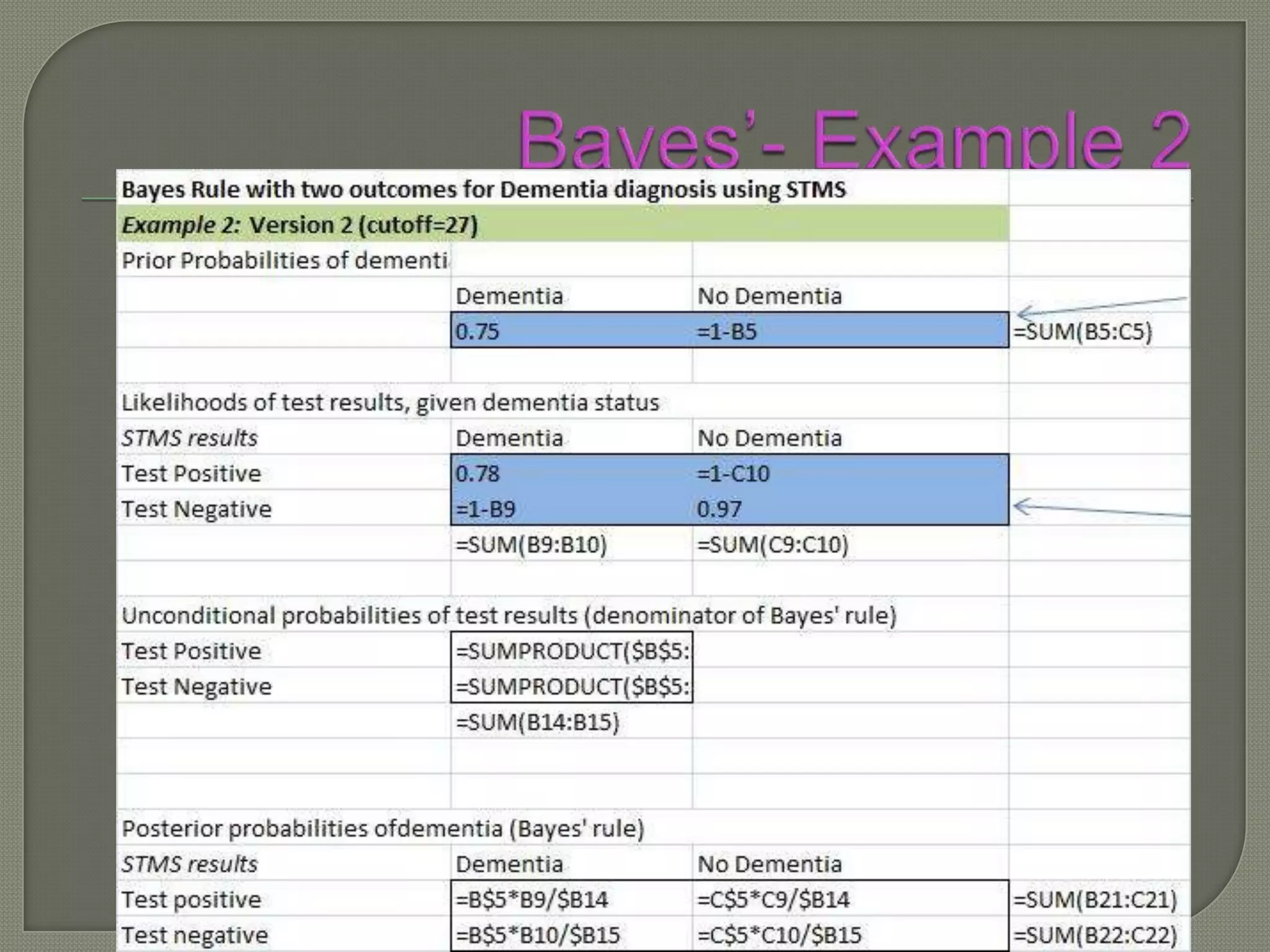
This document discusses Bayes' theorem and how it can be used to determine the post-test probability of a condition based on the pre-test probability, test sensitivity, and test specificity. It provides an example of using Bayes' theorem to calculate the probability that a patient has dementia given that their test result was positive, when the pre-test probability, sensitivity and specificity of the test are known. The key steps of Bayes' theorem are defined.

1. Neuropsychiatric Decision
Making: The Role of
Disorder Prevalence in Diagnostic
Testing
Heather Jacobson, Jessica Landin,
Will Liu, Brian Wiggs

2.  1702-1761
 English Mathematician
 Presbyterian Minister
 Deep interest in probability
 Bayes’ solution to “inverse probability” was
presented after his death, became “Bayes’
Theorem”

3.  Purpose: To revise probabilities as new
information becomes available- i.e., the
probability of our prior probability, given the
result of our conditional probability
• Example: the probability of condition in a patient given
the probability of this condition in the general
population
 The theorem states that the post-test
likelihood of a condition is a function of the
test’s accuracy and the pretest likelihood that
the condition was present.

5.  P(A|B)=(P(B|A) * P(A)) /P(B/A)P(A) + P(B/Not A)P(Not A)
 Where the denominator is an “unconditional probability”
 Prior probability- known before current state
• P(A)
 Likelihood probability- depends on prior node
• P(B/A)
 Posterior Probability-revised probability given new info
• P(A/B)
 Sensitivity- probability that the test will have a positive result
(has a disease) when the person actually has the disease
 Specificity-Probability that the test will be negative when the
person actually lacks the disease

6.  Mr. A Is a 65 year-old male has dementia.
 Dr. X administers the Short Test of Mental
Status (STMS)
 For persons in Mr. A’s age group,
scores<30 are considered diagnostic of
dementia
 STMS has a sensitivity of 95% and
specificity of 88%

7.  Mr. A scores below 30.
 Dr. X should conclude that:
• A.) Mr. A. has a 95% chance of having dementia
• B.) Mr. A has an 88% chance of having dementia
• C.)Mr. A has a 92% chance of having dementia
• D.)She needs more information to specify the
post-test likelihood of dementia

8.  Answer: D
 To specify the post-test likelihood of having
dementia, Dr. X needs to know what the
likelihood of his having dementia before he
was tested
Dr. X needs to use Bayes’ Rule!!

9. Dr. X estimates that before testing
Mr. A has a 75% chance of having
dementia
• Prior probability of dementia:
P(D+)=75%
• Prior probability of no dementia:
P(D-)=25%

10. • Bayes’ Rule:
• D+: has dementia
• D-: does not have dementia
• T+: Test results positive for dementia
• T-: Test results negative for dementia

13.  10,000people in Mr. A’s age group
 75% probability of having dementia =
• 7,500 people with dementia
• 2,500 people without dementia

14.  Administer STMS
• Expect 300 people without dementia to test
positive, given false positive rate of 12%
2,500*12%=300
• Expect 7,125 with dementia to test positive , given
true positive rate is 95%
7,500*95%=7,125
• 7,125+300=7425 positive tests
• P(D+/T+)=7,125/7,425=0.96
Same result as Bayes’ Rule calculation!