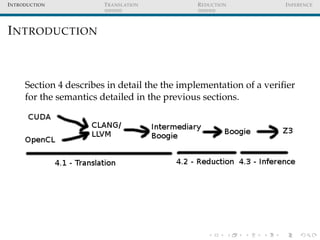
The document provides an in-depth overview of a verifier implementation for GPU semantics, focusing on translation reduction inference and specific challenges related to GPU languages and Boogie. Key topics include handling floating point numbers, pointers, race and barrier divergence checks, and the use of different abstraction strategies for shared-state management. The paper also discusses limitations of the approaches, such as the inability to verify complex shared-state manipulations and the need for invariant inference for race-free code verification.

1. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
GPUVerify
Section 4 - Verification Method
Thomas Wood
November 28, 2012

2. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
I NTRODUCTION
Section 4 describes in detail the the implementation of a verifier
for the semantics detailed in the previous sections.

3. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
T RANSLATION
Compiler from OpenCL/CUDA to intermediary Boogie built
on CLANG/LLVM (a compiler toolset)

4. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
S PECIALISED GPU F EATURES
Although both GPU languages and Boogie are both C-like,
both extend C in different ways.
In particular, GPU languages additionally support:
Vector and Image types
Intrinsic functions supported by the hardware and
compiler eg: advanced maths
Writing translations for these features for Boogie is time
consuming.
(And apparently boring, the paper doesn’t say any more on this)

5. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
B OOGIE AND F LOATS
Boogie doesn’t support floating point numbers directly.
These are often used in GPU Kernels.
Modelled using uninterpreted functions (a function
defined only by signature).
We know something has been assigned, just not its value.
Over-approximation could lead to false-positives, but only
discovered one such case during evaluation.

6. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
P OINTER H ANDLING
Boogie doesn’t support pointers (because they get messy)
GPU Kernels often do less messy things with pointers than
most C code
So, let’s assume that all pointers point within arrays, or are
null, and that anything else is an error
(Variables can be modelled as single-element arrays)
So, pointers can be modelled as a pair: (base, offset)

7. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
P OINTER S EMANTICS
Translation rules of pointer model are straightforward:
Source Generated Boogie
p = A; p = int_ptr(A_base, 0);
p = q; p = q;
foo(p); foo(p);
p = q + 1; p = int_ptr(q.base, q.offset + 1);
if (p.base == A_base)
A[p.offset + e] = d;
p[e] = d; else if (p.base == B_base)
B[p.offset + e] = d;
else assert(false);
if (p.base == A_base)
x = A[p.offset + e];
x = p[e]; else if (p.base == B_base)
x = B[p.offset + e];
else assert(false);

8. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
B UT...
...if the program manipulates pointer in loops, the if...else if
clauses make determining the loop invariants hard.
One solution is to use points-to analysis (Steensgaard’s
algorithm) to determine which arrays a pointer can possibly
point to, and eliminate the impossible branches
if (p.base == A_base)
A[p.offset + e] = d; if (p.base == A_base)
else if (p.base == B_base) → A[p.offset + e] = d;
B[p.offset + e] = d; else assert(false);
else assert(false);

9. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
R EDUCTION OF RACE - AND DIVERGENCE - CHECKING
TO SEQUENTIAL PROGRAM VERIFICATION
Basics have already been discussed in lectures:
Accesses to shared memory are instrumented with logging
procedures
Program transformed to model two arbitrary threads
Checking procedures for race and barrier divergence
introduced

10. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
A N OPEN QUESTION
At the end of the last lecture, we decided that:
P is correct ⇒ All terminating executions of K are free from
data races and barrier divergence.
But:
We might have P incorrect, but all terminating executions of K
free from data races and barrier divergence. Why?

11. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
Recall: Consider:
if (A[0]) {
Stmt translate(Stmt, P) A[tid + 1] = tid;
LOG_READ_A(P$1, e$1); } else {
CHECK_READ_A(P$2, e$2); A[tid + 2] = tid;
x = A[e]; x$1 = P$1 ? * : x$1; }
x$2 = P$2 ? * : x$2;

12. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
Thread 0: Thread 1:
if (false) { if (true) {
... A[2] = 1;
} else { } else {
A[2] = 0; ...
} }
Because we’ve havoced away the shared state!

13. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
A DVERSARIAL A BSTRACTION
The strategy we’ve seen in lectures for shared-state is
Adversarial abstraction - the shared state is thrown away
and havoced.
This over-approximation is fine for cases where the shared
state does not impact upon the control-flow. Otherwise, it
gives false-posititves.

14. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
E QUALITY A BSTRACTION
Both threads keep a shadow copy of the shared-state
At a barrier, the shadow copies are set to be arbitrary, but
equal
On leaving the barrier, all threads have a consistent view
of the shared state
Stmt translatea (Stmt, P) translatee (Stmt, P)
LOG_READ_A(P$1, e$1);
LOG_READ_A(P$1, e$1); CHECK_READ_A(P$2, e$2);
CHECK_READ_A(P$2, e$2); x$1 = P$1 ? A$1[e$1] :
x = A[e]; x$1 = P$1 ? * : x$1; x$1;
x$2 = P$2 ? * : x$2; x$2 = P$2 ? A$2[e$2] :
x$2;
LOG_WRITE_A(P$1, e$1);
CHECK_WRITE_A(P$2, e$2);
LOG_WRITE_A(P$1, e$1); A$1[e$1] = P$1 ? x$1 :
A[e] = x; CHECK_WRITE_A(P$2, e$2); A$1[e$1];
A$2[e$2] = P$2 ? x$2 :
A$2[e$2];

15. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
L IMITATIONS
Unfortunately, Equality Abstraction is far less efficient
than Adversarial Abstraction
GPUVerify only uses Equality Abstraction with the arrays
that require it, this is determined using control
dependence analysis
More complicated uses of the shared-state, such as
A[B[lid]] = ... cannot be verified
This is because B[i] != B[j] cannot be verified, as the
side-effecting actions of other (prior) threads are not
modelled.

16. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
I NVARIANT I NFERENCE
To be able to prove race and barrier-divergence free code, then
the produced Boogie program must be verified.
Verification depends on finding pre and post conditions for the
kernel, and loop invariants within.
GPUVerify uses a heuristically-selected set of invariants and
the Houdini tool to remove invalid invariants from that set
until all can be proven.

17. I NTRODUCTION T RANSLATION R EDUCTION I NFERENCE
M EMORY S TRUCTURE H EURISTICS
The set of invariant heuristics discussed in the paper are for
common data structurings in arrays.
For example, if A[lid + C] = ... occurs in a loop, then a
candidate invariant is
WR EXISTS A ⇒ WR ELEM A − C == lid.