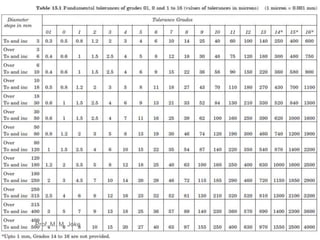
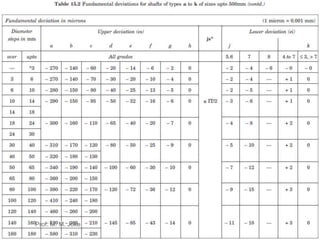
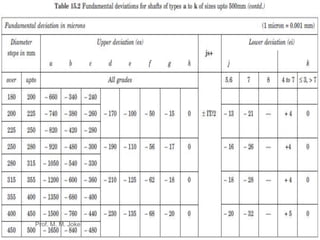
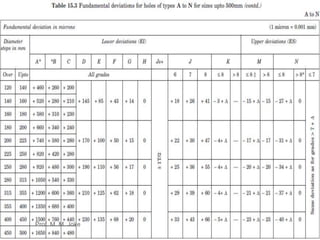
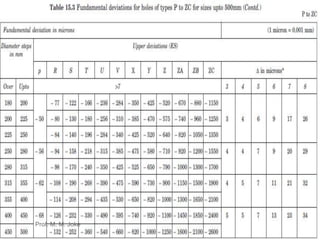
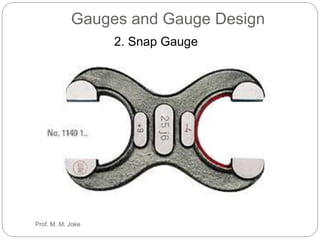
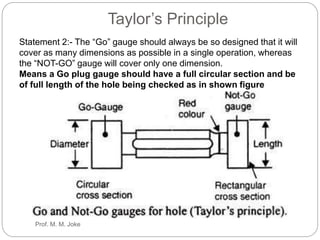
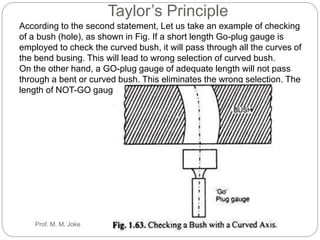
This document discusses limits, fits and tolerances including graphical illustrations of tolerance zones and the fundamental tolerance equation. It provides an example calculation of the tolerance for a grade 7 shaft that is 100mm. Additionally, it covers gauges and gauge design including plug, snap and ring gauges. It discusses multi gauging, inspection and Taylor's principle for gauge design stating that go gauges should cover maximum material condition while not-go gauges cover minimum condition and go gauges check multiple dimensions while not-go gauges check one dimension.

1. Limits, Fits and
Tolerances
Chapter 3
Prof. M. M. Joke

2. Graphical Illustration of Tolerance
Zones
Prof. M. M. Joke

3. IT5 IT6 IT7 IT8 IT9 IT10 IT11 IT12 IT13 IT14 IT15 IT16
7i 10i 16i 25i 40i 64i 100i 160i 250i 400i 640i 1000
i
Relative magnitude of IT tolerances for grades 5 to 16 in terms
of tolerance unit i for sizes upto 500 mm
The fundamental tolerance is a function of the nominal size
and its unit is given by the emperical relation, standard
tolerance unit,
i = 0.45 × 3 √D + 0.001 D
where i is in microns and D is the geometrical mean of the
limiting values of the basic steps mentioned above, in
millimetres. This relation is valid for grades 5 to 16 and
nominal sizes
from 3 to 500 mm.
Prof. M. M. Joke

4. Example 1 Calculate the fundamental tolerance
for a shaft of 100 mm and grade 7.
The shaft size, 100 lies in the basic step, 80 to 120
mm and the geometrical mean is
D = √80 × 120 = 98 mm
The tolerance unit, i = 0.45 * 3 √98 + 0.001 × 98 =
2.172 microns
For grade 7, as per the above table, the value of
tolerance is,
16i = 16 × 2.172 = 35 microns
Prof. M. M. Joke

5. Prof. M. M. Joke

6. Prof. M. M. Joke

7. Prof. M. M. Joke

8. Prof. M. M. Joke

9. Prof. M. M. Joke

10. Prof. M. M. Joke

11. Prof. M. M. Joke

12. Prof. M. M. Joke

13. Prof. M. M. Joke

14. Gauges and Gauge Design
1. Plug Gauge
Prof. M. M. Joke

15. Gauges and Gauge Design
1. Plug Gauge
Prof. M. M. Joke

16. Gauges and Gauge Design
2. Snap Gauge
Prof. M. M. Joke

17. Gauges and Gauge Design
2. Snap Gauge
Prof. M. M. Joke

18. Gauges and Gauge Design
2. Snap Gauge
Prof. M. M. Joke

19. Gauges and Gauge Design
3. Ring Gauge
Prof. M. M. Joke

20. Multi Gauging and Inspection
Eg: 1. Connecting rod Multi
gauging
2. Cam shaft Multi gauging
Prof. M. M. Joke

21. Taylor’s Principle
Statement 1:- The “Go” gauge should always be so
designed that it will cover the maximum metal condition
(MMC), whereas a “NOT-GO” gauge will cover the minimum
(least) metal condition (LMC) of a feature, whether external
or internal.
Prof. M. M. Joke

22. Taylor’s Principle
Statement 2:- The “Go” gauge should always be so designed that it will
cover as many dimensions as possible in a single operation, whereas
the “NOT-GO” gauge will cover only one dimension.
Means a Go plug gauge should have a full circular section and be
of full length of the hole being checked as in shown figure
Prof. M. M. Joke

23. Taylor’s Principle
According to the second statement, Let us take an example of checking
of a bush (hole), as shown in Fig. If a short length Go-plug gauge is
employed to check the curved bush, it will pass through all the curves of
the bend busing. This will lead to wrong selection of curved bush.
On the other hand, a GO-plug gauge of adequate length will not pass
through a bent or curved bush. This eliminates the wrong selection. The
length of NOT-GO gauge is kept smaller than GO-gauge.
Prof. M. M. Joke