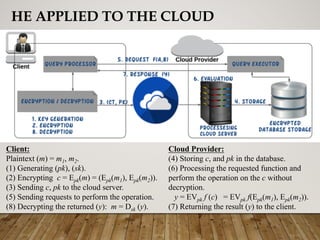
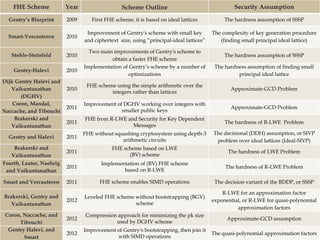
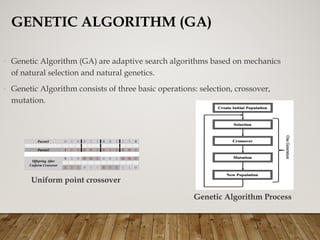
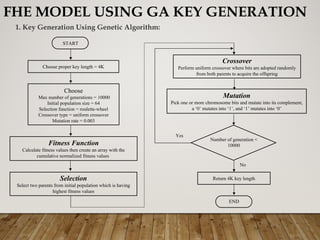
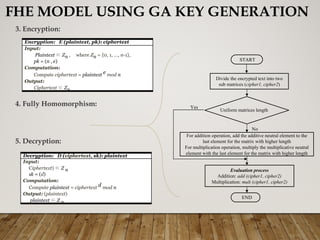
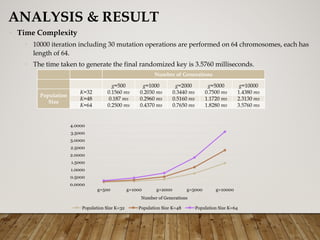
The document presents a genetic algorithm-based key generation approach for fully homomorphic encryption (FHE) aimed at enhancing data security in cloud computing. It outlines the motivation, problem statement, objectives, and proposed methodology for secure outsourcing of computations while preserving client confidentiality. The results demonstrate the effectiveness and efficiency of the proposed scheme, alongside future work suggestions for further improvements.

1. Majedah Alkharji, M.Sc.
Mayyada Al Hammoshi, Ph.D.
Chunqiang Hu, Ph.D.
Hang Liu, Ph.D.
GENETIC ALGORITHM BASED KEY
GENERATION FOR FULLY HOMOMORPHIC
ENCRYPTION
THE CATHOLIC UNIVERSITY OF AMERICA
School of Engineering / Department of
Electrical Engineering and Computer Science

2. • Motivation.
• Statement of Problem.
• Objectives.
• Literature Review.
• Proposed Approach.
• Analysis & Results.
• Conclusion & Future work.
• References.
OUTLINES

3. MOTIVATION - APPLYING ASYMMETRIC
ENCRYPTION TO THE CLOUD

4. • Key Questions:
• How to guarantee that the user’s private data will always be kept safe and
secure?
• Can the cloud service provider be reliable to store and process client’s private
data confidentially?
• Is it possible to ensure that even if the cloud provider have been attacked, client’s
confidential data will not be stolen or reused?
• Problem :
• Performing outsource computation in the cloud while keep the data secure and
confidential.
STATEMENT OF PROBLEM

5. • Design a secure and efficient fully homomorphic encryption cryptographic
scheme to guarantee security services and protect clients’ confidential data for
cloud applications.
• Enable users to perform outsource computations in the cloud without exposing
the original data using FHE.
• Make FHE scheme more secure by getting the maximum randomness from
genetic algorithm.
OBJECTIVES

6. HE APPLIED TO THE CLOUD
Client:
Plaintext (m) = m1, m2.
(1) Generating (pk), (sk).
(2) Encrypting c = Epk(m) = (Epk(m1), Epk(m2)).
(3) Sending c, pk to the cloud server.
(5) Sending requests to perform the operation.
(8) Decrypting the returned (y): m = Dsk (y).
Cloud Provider:
(4) Storing c, and pk in the database.
(6) Processing the requested function and
perform the operation on the c without
decryption.
y = EVpk f (c) = EVpk f(Epk(m1), Epk(m2)).
(7) Returning the result (y) to the client.

7. HISTORY OF HOMOMORPHIC
ENCRYPTION
1978 1982 1994 1998 1999 2000 2005 2009
privacy
Homomorphism
by Rivest,
Adlema, and
Dertouzos
Goldwasser
and Micali
(GM)
(PHE)
Benaloh
(PHE)
Naccache –
Stern (NS)
Okamoto –
Uchiyama
(OU)
(PHE)
Paillier
(PHE)
Damgård
– Jurik
(DJ)
(PHE)
Boneh,
Goh,
and
Nissim
(BGN)
(SWHE)
Craig Gentry
(FHE)

8. EVOLUTION OF FHE
FHE Scheme Year Scheme Outline Security Assumption
Gentry’s Blurprint 2009 First FHE scheme, it is based on ideal lattices The hardness assumption of SSSP
Smart-Vercauteren 2010
Improvement of Gentry's scheme with small key
and ciphertext size, using “principal-ideal lattices”
The complexity of key generation procedure
(finding small principal ideal lattice)
Stehle-Steinfeld 2010
Two main improvements of Gentry's scheme to
obtain a faster FHE scheme
The hardness assumption of SSSP
Gentry-Halevi 2010
Implementation of Gentry’s scheme by a number of
optimizations
The hardness assumption of finding small
principal ideal lattice
Dijk Gentry Halevi and
Vaikuntanathan
(DGHV)
2010
FHE scheme using the simple arithmetic over the
integers rather than lattices
Approximate-GCD Problem
Coron, Mandal,
Naccache, and Tibouchi
2011
Improvement of DGHV working over integers with
smaller public keys
Approximate-GCD Problem
Brakerski and
Vaikuntanathan
2011
FHE from R-LWE and Security for Key Dependent
Messages
The hardness of R-LWE Problem
Gentry and Halevi 2011
FHE without squashing cryptosystem using depth-3
arithmetic circuits
The decisional (DDH) assumption, or SIVP
problem over ideal lattices (Ideal-SIVP)
Brakerski and
Vaikuntanathan
2011
FHE scheme based on LWE
(BV) scheme
The hardness of LWE Problem
Fourth, Lauter, Naehrig
and Vaikuntanathan
2011
Implementation of (BV) FHE scheme
based on R-LWE
The hardness of R-LWE Problem
Smart and Vercauteren 2011 FHE scheme enables SIMD operations The decision variant of the BDDP, or SSSP
Brakerski, Gentry and
Vaikuntanathan
2012
Leveled FHE scheme without bootstrapping (BGV)
scheme
R-LWE for an approximation factor
exponential, or R-LWE for quasi-polynomial
approximation factors
Coron, Naccache, and
Tibouchi
2012
Compression approach for minimizing the pk size
used by DGHV scheme
Approximate-GCD assumption
Gentry Halevi, and
Smart
2012
Improvement of Gentry's bootstrapping, then join it
with SIMD operations
The quasi-polynomial approximation factors

9. • Based on the hardness of ideal lattices.
• Given m = m1, …, mt , c = E [f (m1, …, mt)],
for any function f (+, ✕, ⊕).
• Given a key pair (sk, pk), FHE scheme must have Evaluate function.
• Calculations: performed on E (m1) and E (m2)
Add: E (m1+ m2). Multiply: E (m1 ✕ m2).
• Circular security - The process of sk encryption under pk.
• Re-crypt algorithm - that takes a ciphertext E(m1) or E(m2) with noise N'< N
and provide a “new” ciphertext.
Gentry's Steps: Constructing a SWHE scheme, Squashing the decryption scheme,
then Bootstrapping.
GENTRY -

10. • Genetic Algorithm (GA) are adaptive search algorithms based on mechanics
of natural selection and natural genetics.
• Genetic Algorithm consists of three basic operations: selection, crossover,
mutation.
GENETIC ALGORITHM (GA)
Uniform point crossover
Parent1 0 1 0 0 1 1 0 0 1 1 1 0
Parent2 1 1 1 0 0 1 0 1 1 0 0 1
Offspring After
Uniform Crossover
0 1 0 0 0 1 0 0 1 0 0 1
1 1 1 0 1 1 0 1 1 1 1 0
Genetic Algorithm Process

11. 1) Public Key Cryptography Using Genetic Algorithm (Mishra & Siddharth )
• Provides effective and enhanced performance outcomes with feasible and practical
implementation.
2) Key Generation Using Genetic Algorithm for Image Encryption (Soni &
Agrawal)
• Random number generator (RNG) is used to generate key and genetic algorithm
(GA) is further used to make the key more complex.
3) Selection of Fittest Key Using Genetic Algorithm and Autocorrelation in
Cryptography (Jawaid et al.,)
• The keys obtained are tested for randomness by using the autocorrelation test to
check whether the random numbers generated is independent in sequence or not.
GA LITERATURE REVIEW

12. 1. Key Generation Using Genetic Algorithm:
FHE MODEL USING GA KEY GENERATION
Choose proper key length = 4K
Choose
Max number of generations = 10000
Initial population size = 64
Selection function = roulette-wheel
Crossover type = uniform crossover
Mutation rate = 0.003
Fitness Function
Calculate fitness values then create an array with the
cumulative normalized fitness values
Selection
Select two parents from initial population which is having
highest fitness values
Crossover
Perform uniform crossover where bits are adopted randomly
from both parents to acquire the offspring
Mutation
Pick one or more chromosome bits and mutate into its complement,
a ‘0’ mutates into ‘1’, and ‘1’ mutates into ‘0’
Number of generation <
10000
Yes
Return 4K key length
No
END
START

13. 2. Modulo Keys Creation from GA Inputs:
FHE MODEL USING GA KEY GENERATION
Yes
Pick two prime numbers from the generated
key that matches the RSA conditions
Compute n = p. q
Compute φ(n) = (p – 1). (q - 1)
Yes
Not found
gcd (prime array (i), p)
If gcd (prime array(i), p) = 1
No
No
Not found e
if (i < φ(n)) & (gcd (prime array(i),
φ(n)) = 1
No
No
Yes
e = i
End of matrix of prime
numbers
START
Yes
Return d = i
Yes
q = prime array (i)
mod (e * i , φ(n)) =1
No
Yes
END

14. 3. Encryption:
4. Fully Homomorphism:
5. Decryption:
FHE MODEL USING GA KEY GENERATION
Decryption: D (ciphertext, sk): plaintext
Input:
Ciphertext) ∈ Z n
sk = (d)
Computation:
Compute plaintext = ciphertext d mod n
Output: (plaintext)
plaintext ∈ Z n
Encryption: E (plaintext, pk): ciphertext
Input:
Plaintext ∈ Zn , where Zn = {0, 1, …, n-1},
pk = (n , e)
Computation:
Compute ciphertext = plaintext e mod n
Output:
Ciphertext ∈ Zn
Divide the encrypted text into two
sub matrices (cipher1, cipher2)
For addition operation, add the additive neutral element to the
last element for the matrix with higher length
For multiplication operation, multiply the multiplicative neutral
element with the last element for the matrix with higher length
Uniform matrices length
Yes
Evaluation process
Addition: add (cipher1, cipher2)
Multiplication: mult (cipher1, cipher2)
No
START
END

15. 0.0000
0.5000
1.0000
1.5000
2.0000
2.5000
3.0000
3.5000
4.0000
g=500 g=1000 g=2000 g=5000 g=10000
Number of Generations
Population Size K=32 Population Size K=48 Population Size K=64
• Time Complexity
• 10000 iteration including 30 mutation operations are performed on 64 chromosomes, each has
length of 64.
• The time taken to generate the final randomized key is 3.5760 milliseconds.
ANALYSIS & RESULT
Number of Generations
g=500 g=1000 g=2000 g=5000 g=10000
Population
Size
K=32 0.1560 ms 0.2030 ms 0.3440 ms 0.7500 ms 1.4380 ms
K=48 0.187 ms 0.2960 ms 0.5160 ms 1.1720 ms 2.3130 ms
K=64 0.2500 ms 0.4370 ms 0.7650 ms 1.8280 ms 3.5760 ms

16. • The Nature of Randomness
• Degree of movement test is calculated to observe the level of randomness in the GA final key.
• The test shows that the final population has ‘0’ correlation with the initial one.
ANALYSIS & RESULT
Length
Population
Size
341 479 388 442 502 424 295 261 261 454
357 358 363 275 441 288 377 443 382 293
301 458 478 435 345 425 309 394 297 407
342 487 506 270 325 422 310 375 397 294
454 275 372 350 464 462 509 270 484 498
280 341 336 344 363 301 330 312 391 385
412 358 326 294 314 349 435 297 419 268
380 395 286 406 270 488 351 318 381 407
260 328 347 445 404 350 399 345 494 489
490 257 433 334 299 454 293 282 318 306

17. • Applying Genetic Algorithm to generate strong, non-repeating, high-quality
random keys will enhance the security of FEH schemes.
• Results depict the effectiveness of the proposed scheme under two different
scenarios.
• The proposed scheme proves the key randomness with a very low running time
compared to the existing schemes.
• Future Work will be FHE based on machine learning with Error (LWE).
CONCLUSION & FUTURE WORK

18. [1] C. Gentry, “Fully homomorphic encryption using ideal lattices,” STOC'09 Proceedings of the forty-first
annual ACM symposium on Theory of computing, 2009, pp. 169–178.
[2] S. Mishra, and S. Bali, “Public Key Cryptography Using Genetic Algorithm,” International Journal of
Recent Technology and Engineering (IJRTE), 2013, vol. 2, pp. 150-54.
[3] A. Soni, and S. Agrawal, “Key Generation Using Genetic Algorithm for Image Encryption,”
International Journal of Computer Science and Mobile Computing (IJCSMC), 2013, Vol. 2, pp. 376 – 383.
[4] S. Jawaid, A. Saiyeda, and N. Suroor, “Selection of Fittest Key Using Genetic Algorithm and
Autocorrelation in Cryptography,” Journal of Computer Sciences and Applications (JCSA), 2015, vol. 3, pp.
46-51.
[5] Z. Brakerski, and V. Vaikuntanathan, “Efficient Fully Homomorphic Encryption from (Standard)
LWE,” FOCS’11 Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer
Science, 2011, pg. 97-106.
[6] M. van Dijk, C. Gentry, S. Halevi, and V. Vaikuntanathan, “Fully Homomorphic Encryption over the
Integers,” Advances in Cryptology – EUROCRYPT, 2010, vol. 6110, pp. 24-43.
BIBLIOGRAPHY

19. ?
QUESTIONS