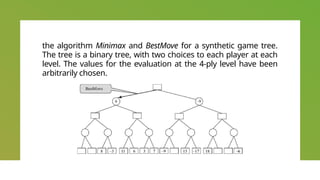
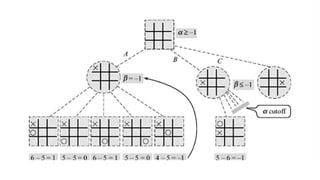
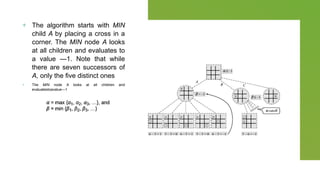
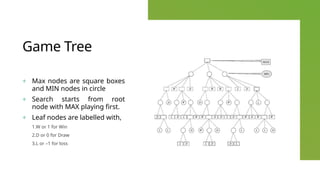
The document discusses unit 4 covering topics in game playing, planning, and constraint satisfaction, focusing on algorithms like minimax and alpha-beta for decision-making in board games. It explains concepts such as game trees, max and min nodes, evaluation functions, and the strategies players must adopt to optimize their chances of winning. Moreover, it highlights the importance of strategies and the evaluation of game states in determining optimal moves in various games like chess and tic-tac-toe.

1. UNIT 4 GAME
PLAYING,
PLANNING AND
CONSTRAINT
SATISFACTION

2. TOPICS COVERED
+ BOARD GAMES
+ GAME PLAYING ALGORITHM
+ ALGORITHM MINIMAX
+ ALGORITHM ALPHA BETA
+ B* SERACH
+ LIMITATION OF SEARCH
+ STRIPS DOMAIN
+ FORWARD STATE SPACE PLANNING
+ BACKWARD STATE
SPACE PLANNING
+ GOAL STACK PLANNING
+ PLAN SPACE PLANNING
+ CONSTRAINT SATISFACTION
PROBLEM
+ N- QUEENS

3. Games?
+ Games provide a well-defined environment in which states are
discrete
+ It is not need to worry about input and output in a complex
environment but focus entirely on decision making
+ Multi agent activity (Interaction between agents)

4. Board games : Two player only
+ Two person: Two players are involved in the game
+ Zero sum: One player will win the game and other losses
+ Complete information: Both information is accessible to both
player
+ Alternate note: The players take turns to make moves
+ Deterministic game: No element of chance in the moves that
player can make eg: Dice

5. Game tree
To represent complete information of
the game
By assumption the game is zero sum.
The two player are namely MIN and
MAX indicating the goals are opposite
to each other.
A game tree is layered tree in which at
each alternating level one or the
other player makes the choice. This
layers are called MIN and MAX layers

6. Game Tree
+ Max nodes are square boxes
and MIN nodes in circle
+ Search starts from root
node with MAX playing first.
+ Leaf nodes are labelled with,
1.W or 1 for Win
2.D or 0 for Draw
3.L or –1 for loss

7. Game Tree
+ The leaves of the game tree is
labelled with the outcome of the
game and the game ends there.
+ The task of each player is to
choose the move when
its turn comes.
+ MAX player: who prefers the
maximum valued outcome
+ MIN player: who prefer the
minimum valued outcome

8. Game tree
+ It is possible to analyze the game and determine the
outcome when both the player play perfectly
+ Backing up values from the leaf node up of the root.
MinMax rule
+ If a node is a MAX node, backup the maximum of the value
of its children
Value (node)=max {value(c) | c is a child of node}
+ If a node is a MAX node, backup the minimum of the value of
its children
Value (node)=min {value(c) | c is a child of node}

9. Game tree
+ Given a set of choices with known
outcome. MAX will choose a node
that yield the value =1, if available
else 0 is available then –1 (if-f all the
children are labelled with –1).
+ MIN tries to win the game, to win the
game, to win the node must be
labelled with -1.

10. Game tree
+ Arrows show the value backed up.
+ It identifies the best move for each
player
+ When more than one more is best,
all are marked.
+ MAX wins the game backed up
value is w.

11. Game Tree
+ A game playing program is required to produce the moves
for a player traditionally MAX
+ MinMax value determines the best that MAX can do against
a perfect opponent, this involves computing minimax values
+ The choice of the player is represented by strategy
+ A strategy is a subtree of a game tree that freezes the
choices for the player

12. Game Tree
+ Strategy represents the choices of one
player
+ The outcome of the game depends on the
opponent.
+ If opponent plays good, the value of the
strategy for MAX will be the minimum
value of a leaf node because MIN
will drive the game.
+ The optimal strategy for MAX is the
strategy with the highest value.
+ If this happened to be 1 then MAX has a
winning strategy.

13. Game Tree
+ If both the players is to find
their optimal strategies. Then the
game is played with the path that
is intersection of two strategies
+ Selection of strategy requires solving
the game tree
+ Finding the strategy is like solving
the game tree as an And or Problem
+ Game tree for Tic-Tac-Toe is small
whereas for chess is large

14. Evaluation function
+ If minimax value is computed then we can select the move that is
known to be best.
+ Like heuristic function, it is evaluation function
+ It tells us how good a given position is from the prespective of MAX
+ The outcome of the game is a value from the set { 1,0,-1}
+ The evaluation function is applied on the intermediate node of the
tree, because we cannot evaluate the full tree since the game is not
complete

15. Evaluation function
+ The range of the evaluation function is in the interval [-1,1]
+ It determines who is in the winning state
+ If Evalution function is 0.5 then MAX appears to win
+ If Evalution function is –0.9 then MIN appears to win
+ If Evalution function is 0 then it is not indicating draw because in practice
it is 1000 to –1000 and computed as a sum of values of good features.
+ Eg: In chess, evaluation function is computed by using material value and
positional value

16. Game playing
algorithm
+ Game playing algorithm will explore
the tree up to finite ply depth.
+ Compute the evaluation function of
the node on the frontier.
+ Use minimax rule to backup rule, to
determine the value of partial game
tree and the best move
+ Make the best move and wait for
the opponents move and again
search for best move.

17. + If we could have searched the entire tree, the search would have to be done only
once.
+ But constrained to search only a part of a tree, we do a series of searches, one
every time the program has to make a move.
+ Every subsequent search starts two plies deeper than the previous one, and
explores two more plies in the game tree.

18. + A game playing program does a k-ply
look-ahead search for each move. It
makes the best move, waits for the
opponent to move, and does another
k-ply search to decide upon the next
move
+ the series of fixed ply searches explore
only a small part of the entire game
tree. Assuming that each search looks
at P nodes, the game playing program
will look at a total of PNI2 nodes during
the entire time, where N is the number
of moves made by both sides.
+
the basic algorithm for doing the fixed
ply search. The algorithm uses an
evaluation function e(J) when
considering the nodes at the frontier.

19. Algorithm MINI MAX
+ The algorithm Minimax searches the game tree till depth k in a depth-first manner from
left to right.
+ It applies the minimax rule to determine the value of the root node.
+ The algorithm uses a test Terminal(node) to determine whether it is looking at a frontier
node, and therefore should apply the evaluation function e(J) instead of making a
recursive call.
+ A node is a terminal of a leaf node of the game, and will evaluate to one of{—Large, 0,
+Large } or it is a node on the horizon, and in that case the evaluation function e(J) will be
applied.
+ It will need incorporation of a depth parameter k, perhaps passed along with the node,
decremented at each recursive call.
+ It will become zero when the node is on the horizon.

20. Algorithm MINI MAX
+ The MINIMAX algorithm recursively
calls itself till it reaches a terminal
node. A terminal node is either a leaf
of the game tree or a node at depth
k. The algorithm does a k-ply search
from left to right. Note that the
recursive calls are of decreasing ply
depth. One will need to keep track of
depth of a node.

21. Algorithm MINI MAX
+ The minimax value is returned but
not the best move that leads to that
value. Since the objective is to play
the game, the following version
returns the best move.
+ It calls the above Minimax algorithm
for each successor of the root, and
keeps track of the best move as well
as the best board value.

22. Algorithm MINI MAX
+ The algorithm BestMove accepts
a board position and returns the
best move for MAX. It calls
algorithm Minimax with each of
its successors and keeps track of
which successor yields the best
value.

23. the algorithm Minimax and BestMove for a synthetic game tree.
The tree is a binary tree, with two choices to each player at each
level. The values for the evaluation at the 4-ply level have been
arbitrarily chosen.

24. + The Minimax algorithm above is the one that is doing the search. The
BestMove algorithm is simply a modification to keep track of the best
move found by Minimax.
+ The algorithm BestMove calls algorithm Minimax for each of
the successors of root, which computes the minimax value of each
of them. It then chooses the best successor and returns that as the best
move.
+ The algorithm Minimax finds the best move after searching the entire
tree k-ply deep. There are, however, situations when it is not necessary
to continue searching. This happens when it is known that searching
further does have any scope of improvement.

25. Algorithm AlphaBeta
+ the game tree is viewed as a supply-chain process. At the top level, MAX has a set of MIN suppliers, from
which it will select the one with the maximum value. Likewise, each MIN has MAX suppliers, from which the
one with the lowest valued one will be selected.
+ As the search in algorithm Minimax continues from the left to right, each node on the search frontier
has been partially evaluated
+ The partially (or fully) known values of MAX nodes as a values.
+ These values are lower bounds on the value of the MAX node. This is because that the MAX node will
only accept higher values from the unevaluated successors.
+ MAX nodes are also known as Alpha nodes. Likewise, MIN nodes are also called Beta nodes and store b
values, which are upper bounds on values of the concerned MIN nodes
+ Remember that the a and b values are values that are already available to the respective nodes. They
are not going to be interested in any successors that offer something inferior. Not only that, they are
not going to be interested in any descendant that does not offer a better value.

26. Algorithm
AlphaBeta
+ The search frontier
contains a partial path
in the game tree in
which nodes have been
partially evaluated. As
this frontier sweeps to
the right, these node
will get fully evaluated.

27. + The example is from the Noughts and Crosses game.
We assume a 2-ply search, in which the following
evaluation function is used,
+ e(J) = (numbers of rows, columns and diagonals
available to MAXj — (number of rows, columns and
diagonals available to MIN)

29. + The algorithm starts with MIN
child A by placing a cross in a
corner. The MIN node A looks
at all children and evaluates to
a value —1. Note that while
there are seven successors of
A, only the five distinct ones
+ The MIN node A looks at all children and
evaluatestoavalue—1