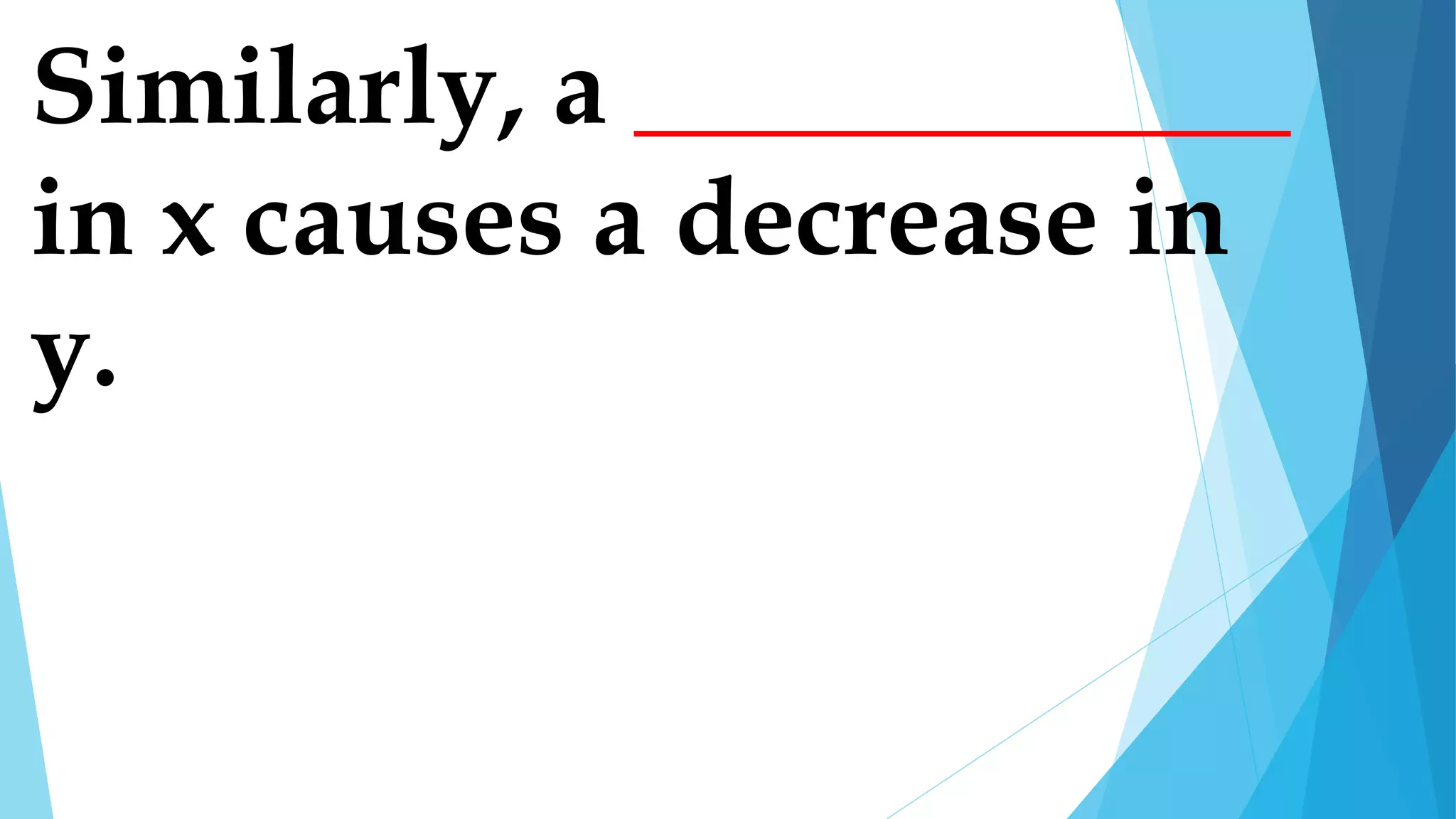This document discusses direct variation and provides examples of how it applies in various situations. It begins by establishing the objectives of identifying practical situations involving direct variation and illustrating how to translate it into mathematical equations. Examples are then provided to demonstrate direct variation, including how the cost of rice increases as the number of kilograms increases. Students are asked to complete statements and equations to practice applying direct variation. Real-world examples like cooling rates are also used to reinforce understanding.