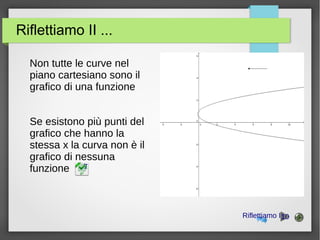
Il documento presenta un'introduzione alle funzioni matematiche, definendo una funzione come una relazione che associa ogni elemento di un insieme a un solo elemento di un altro insieme. Viene discusso il concetto di immagine e controimmagine, nonché il grafico di una funzione nel piano cartesiano, evidenziando che non tutte le curve rappresentano una funzione. Infine, il documento include risorse per le icone utilizzate.

1. INTRODUZIONE ALLE FUNZIONI
Serena Fuschini

2. Piano della presentazione
Considerazioni preliminari
Per cominciare...
Definizione
Riflettiamo I ...
Immagine, Controimmagine
Grafico
Riflettiamo II ...
Lettura dell'immagine
Lettura della controimmagine
4
5
6
8
9
3
10
11
12
7
2

3. Considerazioni peliminari
Le funzioni costituiscono un nucleo essenziale su cui
costruire le competenze matematiche
(documenti UMI-CIIM - Matematica 2003 )
Le funzioni sono uno strumento per studiare molti
fenomeni attraverso un modello matematico
(elaborazione immagini elaborazione suono )
.
3
.

4. Per cominciare...
4

5. Definizione
Una funzione f: A B è
una relazione da A a B che
associa ad ogni elemento
dell'insieme A un solo
elemento dell'insieme B.
A dominio di f
B codominio di f
1
5

6. Riflettiamo I...
La definizione sottintende due distinte condizioni:
Ogni elemento
di A è in relazione con
un qualche elemento di B
Un generico elemento di A è
in relazione con un solo
elemento di B
6

7. ...
Una relazione f NON è una funzione se:
● Esiste almeno un elemento di A che non è in relazione con
nessun elemento di B
OPPURE
● Esiste almeno un elemento di A che è in relazione con più di un
elemento di B 3
2
Riflettiamo II 7

8. Immagine, Controimmagine
Data una funzione f : A B,
● l'immagine di un elemento x di A tramite f è l'elemento di B
associato a x
● la controimmagine di un elemento y di B è formata dagli
elementi di x che hanno y come immagine 5
4
Lettura dell'immagine Lettura della controimmagine
8

9. Grafico
Data una funzione f: A B
Il sottoisieme di AxB
Gr(f):={(x,y) | y=f(x)}
si chiama grafico di f 6
9

10. Riflettiamo II ...
Non tutte le curve nel
piano cartesiano sono il
grafico di una funzione
Se esistono più punti del
grafico che hanno la
stessa x la curva non è il
grafico di nessuna
funzione 7
Riflettiamo I10

11. Lettura dell'immagine
Scegliere un valore del
dominio sull'asse x
Individuare il punto
corrispondente sul grafico
(avente la x uguale al
valore scelto)
Individuare sull'asse y il
corrispondente valore
dell'ordinata
8
Immagine, Controimmagine 11

12. Lettura della controimmagine
Scegliere un valore del
codominio sull'asse y
Individuare i corrispondenti
punti (se esistono) sul
grafico (aventi la y uguale
al valore scelto)
Individuare sull'asse x i
corrispondenti valori delle
ascisse (se esistono)
9
Immagine, Controimmagine 12

13. Risorse utilizzate
Le seguenti icone sono tratte dal sito IconArchive
Artista: TraYse101
Iconset: Basic Filetypes 2 Icons
Licenza: Free per uso non commerciale.
Uso commerciale: non consentito
Gif Url Pdf Wav
.
13

14. L'icona è tratta dall'immagine di Pixabay
L'icona è tratta dall'immagine di Pixabay
Le immagini 1 e 2 utilizzate sono tratte da Pixabay
Il suono utilizzato è tratto da Freesound