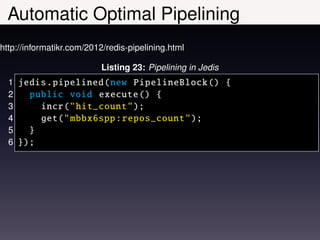
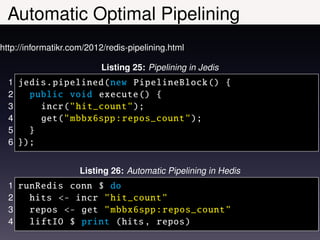
The document discusses the concept of monoids in functional algebra, focusing on their definitions, structure, and laws. It explores their application in programming, particularly in Haskell and Scala, and emphasizes their properties, type safety, and generic functions. The text also covers examples, type classes, and the relationship between monoids, semigroups, and groups.

1. Functional Algebra
Monoids Applied
Susan Potter
Nov 10, 2012

2. OMG, Algebra? FML.. . .

3. OMG, Algebra? FML.. . .
Figure: Chill! Algebra is just a domain specific language

4. % whoami
Figure: From OO patterns to FP abstractions

5. Monoids: What are they?
An abstraction (laws)
not a design pattern (forces, context, . . . )
Algebraic structure . . .
over a set with a binary operator and an identity element
Accumulator . . .
Its sole purpose
Special case category . . .
with only one object

6. Monoids: What are they?
An abstraction (laws)
not a design pattern (forces, context, . . . )
Algebraic structure . . .
over a set with a binary operator and an identity element
Accumulator . . .
Its sole purpose
Special case category . . .
with only one object

7. Monoids: What are they?
An abstraction (laws)
not a design pattern (forces, context, . . . )
Algebraic structure . . .
over a set with a binary operator and an identity element
Accumulator . . .
Its sole purpose
Special case category . . .
with only one object

8. Monoids: What are they?
An abstraction (laws)
not a design pattern (forces, context, . . . )
Algebraic structure . . .
over a set with a binary operator and an identity element
Accumulator . . .
Its sole purpose
Special case category . . .
with only one object

9. Monoids: Typeclasses
Listing 1: Haskell Monoid Typeclass Definition
1 -- | In Haskell Prelude Data. Monoid
2 class Monoid a where
3 mempty :: a -- identity
4 mappend :: a -> a -> a -- binary op
5 mconcat :: [a] -> a -- helper
Listing 2: Scalaz Monoid Trait Definition
1 // Scalaz 7’s Monoid typeclass definition , kinda
2 trait Monoid [A] extends Semigroup [A] { self =>
3 def zero: A /* identity */
4 def append(x: A, y: => A): A /* binary op */
5 }
6 // from SemigroupOps [A] ...
7 final def |+|(other: => A): A = A.append(self, other)

10. Monoids: Typeclasses
Listing 3: Haskell Monoid Typeclass Definition
1 -- | In Haskell Prelude Data. Monoid
2 class Monoid a where
3 mempty :: a -- identity
4 mappend :: a -> a -> a -- binary op
5 mconcat :: [a] -> a -- helper
Listing 4: Scalaz Monoid Trait Definition
1 // Scalaz 7’s Monoid typeclass definition , kinda
2 trait Monoid [A] extends Semigroup [A] { self =>
3 def zero: A /* identity */
4 def append(x: A, y: => A): A /* binary op */
5 }
6 // from SemigroupOps [A] ...
7 final def |+|(other: => A): A = A.append(self, other)

11. Monoids: Typeclasses
Listing 5: Haskell Monoid Typeclass Definition
1 -- | In Haskell Prelude Data. Monoid
2 class Monoid a where
3 mempty :: a -- identity
4 mappend :: a -> a -> a -- binary op
5 mconcat :: [a] -> a -- helper
Listing 6: Scalaz Monoid Trait Definition
1 // Scalaz 7’s Monoid typeclass definition , kinda
2 trait Monoid [A] extends Semigroup [A] { self =>
3 def zero: A /* identity */
4 def append(x: A, y: => A): A /* binary op */
5 }
6 // from SemigroupOps [A] ...
7 final def |+|(other: => A): A = A.append(self, other)

12. Monoids: Typeclasses
Listing 7: Haskell Monoid Typeclass Definition
1 -- | In Haskell Prelude Data. Monoid
2 class Monoid a where
3 mempty :: a -- identity
4 mappend :: a -> a -> a -- binary op
5 mconcat :: [a] -> a -- helper
Listing 8: Scalaz Monoid Trait Definition
1 // Scalaz 7’s Monoid typeclass definition , kinda
2 trait Monoid [A] extends Semigroup [A] { self =>
3 def zero: A /* identity */
4 def append(x: A, y: => A): A /* binary op */
5 }
6 // from SemigroupOps [A] ...
7 final def |+|(other: => A): A = A.append(self, other)

13. Monoids: Laws
Closure: ∀a, b ∈ S : ab ∈ S
for all a and b in set S, the result of a and b given to the binary operator
is also in set S.
Associativity: ∀a, b, c ∈ S : (ab)c = a(bc)
for all a, b, and c in set S, either binary operator can be evaluated first
to produce same result.
Identity: ∃e ∈ S : ∀a ∈ S : ea = a = ae
there exists an e in set S such that for all a in set S ea evaluates to a
and is equal to ae

14. Monoids: Laws
Closure: ∀a, b ∈ S : ab ∈ S
for all a and b in set S, the result of a and b given to the binary operator
is also in set S.
Associativity: ∀a, b, c ∈ S : (ab)c = a(bc)
for all a, b, and c in set S, either binary operator can be evaluated first
to produce same result.
Identity: ∃e ∈ S : ∀a ∈ S : ea = a = ae
there exists an e in set S such that for all a in set S ea evaluates to a
and is equal to ae

15. Monoids: Laws
Closure: ∀a, b ∈ S : ab ∈ S
for all a and b in set S, the result of a and b given to the binary operator
is also in set S.
Associativity: ∀a, b, c ∈ S : (ab)c = a(bc)
for all a, b, and c in set S, either binary operator can be evaluated first
to produce same result.
Identity: ∃e ∈ S : ∀a ∈ S : ea = a = ae
there exists an e in set S such that for all a in set S ea evaluates to a
and is equal to ae

16. Monoids: Properties (Haskell)
1 -- property based tests for monoid "laws"
2 -- does not compile yet; must specify type a
3 module Tests where
4 import Test. QuickCheck ( quickCheck )
5
6 -- closure law verified by type system
7
8 propMonoidAssoc :: Monoid a => a -> a -> a -> Bool
9 propMonoidAssoc x y z =
10 mappend ( mappend x y) z == mappend x ( mappend y z)
11
12 propMonoidIdent :: Monoid a => a -> Bool
13 propMonoidIdent x =
14 mappend mempty x == x && mappend x mempty == x

17. Monoids: Simple "Natural" Examples
Listing 9: Haskell
1 -- OP ID List
2 foldr (+) 0 [1 ,2 ,3 ,4] -- 10
3 foldr (*) 1 [1 ,2 ,3 ,4] -- 24
4 foldr (++) [] [[1] , [1 ,2]] -- [1 ,1 ,2]
5 foldr (&&) True [True , False , True] -- False
6 foldr (||) False [True , False , True] -- True
7

18. Monoids: Simple "Natural" Examples
Listing 11: Haskell
1 -- OP ID List
2 foldr (+) 0 [1 ,2 ,3 ,4] -- 10
3 foldr (*) 1 [1 ,2 ,3 ,4] -- 24
4 foldr (++) [] [[1] , [1 ,2]] -- [1 ,1 ,2]
5 foldr (&&) True [True , False , True] -- False
6 foldr (||) False [True , False , True] -- True
7

19. Monoids: Simple "Natural" Examples
Listing 13: Haskell
1 -- OP ID List
2 foldr (+) 0 [1 ,2 ,3 ,4] -- 10
3 foldr (*) 1 [1 ,2 ,3 ,4] -- 24
4 foldr (++) [] [[1] , [1 ,2]] -- [1 ,1 ,2]
5 foldr (&&) True [True , False , True] -- False
6 foldr (||) False [True , False , True] -- True
7

20. Monoids: Simple "Natural" Examples
Listing 15: Haskell
1 -- OP ID List
2 foldr (+) 0 [1 ,2 ,3 ,4] -- 10
3 foldr (*) 1 [1 ,2 ,3 ,4] -- 24
4 foldr (++) [] [[1] , [1 ,2]] -- [1 ,1 ,2]
5 foldr (&&) True [True , False , True] -- False
6 foldr (||) False [True , False , True] -- True
7 mconcat = foldr mappend mempty

21. Monoids: Simple "Natural" Examples
Listing 17: Haskell
1 -- OP ID List
2 foldr (+) 0 [1 ,2 ,3 ,4] -- 10
3 foldr (*) 1 [1 ,2 ,3 ,4] -- 24
4 foldr (++) [] [[1] , [1 ,2]] -- [1 ,1 ,2]
5 foldr (&&) True [True , False , True] -- False
6 foldr (||) False [True , False , True] -- True
7 mconcat = foldr mappend mempty
Listing 18: Same in Scala: WTF?
1 List (1 ,2 ,3 ,4). foldRight (0)(_+_) // 10
2 List (1 ,2 ,3 ,4). foldRight (1)(_*_) // 24
3 List(List (1), List (1 ,2)). foldRight (List[Int ]())( _++_)
4 List(true ,false ,true ). foldRight (true )(_&&_)
5 List(true ,false ,true ). foldRight ( false )(_||_)

22. Monoids: Define Your Own (Haskell)
Listing 19: Haskell Monoid Definition
1 import Data. Monoid
2
3 data Asset = Cash Int
4 | Receivables Int ...
5 data Liability = NotesPayable Int
6 | AccountsPayable Int ...
7 -- naive , but illustrative
8 data BalSheet = BalSheet [ Asset ] [ Liability ]
9
10 instance Monoid BalSheet where
11 mempty :: m
12 mempty = BalSheet [] []
13 mappend :: m -> m -> m
14 mappend ( BalSheet a1 l1) ( BalSheet a2 l2) =
15 BalSheet ( mappend a1 a2) ( mappend l1 l2)

23. Monoids: Define Your Own (Scala)
Listing 20: Scalaz Monoid Definition
1 import scalaz ._; import Scalaz ._;
2
3 // naive , but illustrative
4 case class Portfolio ( positions : Seq[ Position ])
5 object Portfolio {
6 implicit val portfolioMonoid =
7 new Monoid [ Portfolio ] {
8 def append (p1: Portfolio , p2: Portfolio ) =
9 Portfolio ( append (p1.positions , p2. positions ))
10 def zero = Portfolio (Seq. empty )
11 }
12 }

24. Monoids: So what?
Properties "Interface"
Once you understand one monoid, you understand them all; simpler
layers => simpler tests
Type Safe & Type Expressive
Can mappend A s but not a A and a B where A ! = B and
myCalc :: Monoid a => a -> b
Generic Functions
e.g. consolidate = foldr mappend mempty
Highly Applicable
Look around your domain. Do you see Monoids Everywhere™ yet?

25. Monoids: So what?
Properties "Interface"
Once you understand one monoid, you understand them all; simpler
layers => simpler tests
Type Safe & Type Expressive
Can mappend A s but not a A and a B where A ! = B and
myCalc :: Monoid a => a -> b
Generic Functions
e.g. consolidate = foldr mappend mempty
Highly Applicable
Look around your domain. Do you see Monoids Everywhere™ yet?

26. Monoids: So what?
Properties "Interface"
Once you understand one monoid, you understand them all; simpler
layers => simpler tests
Type Safe & Type Expressive
Can mappend A s but not a A and a B where A ! = B and
myCalc :: Monoid a => a -> b
Generic Functions
e.g. consolidate = foldr mappend mempty
Highly Applicable
Look around your domain. Do you see Monoids Everywhere™ yet?

27. Monoids: So what?
Properties "Interface"
Once you understand one monoid, you understand them all; simpler
layers => simpler tests
Type Safe & Type Expressive
Can mappend A s but not a A and a B where A ! = B and
myCalc :: Monoid a => a -> b
Generic Functions
e.g. consolidate = foldr mappend mempty
Highly Applicable
Look around your domain. Do you see Monoids Everywhere™ yet?

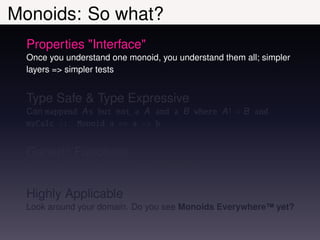
28. Monoids: But . . .
Types With Multiple Monoids
More boilerplate though usually manageable. e.g.
Listing 21: Haskell Monoid Typeclass Definition
1 import Data. Monoid
2 toSums = map Sum
3 mconcat $ toSums [1 ,2 ,3 ,4] -- 10
4
5 toAlls = map All
6 getAll $ mconcat $ toAlls [True , False , True]
Think!
Does it make sense to declare Vector as a Monoid in Haskell?

29. Monoids: But . . .
Types With Multiple Monoids
More boilerplate though usually manageable. e.g.
Listing 22: Haskell Monoid Typeclass Definition
1 import Data. Monoid
2 toSums = map Sum
3 mconcat $ toSums [1 ,2 ,3 ,4] -- 10
4
5 toAlls = map All
6 getAll $ mconcat $ toAlls [True , False , True]
Think!
Does it make sense to declare Vector as a Monoid in Haskell?

30. Automatic Optimal Pipelining
http://informatikr.com/2012/redis-pipelining.html
Listing 23: Pipelining in Jedis
1 jedis . pipelined (new PipelineBlock () {
2 public void execute () {
3 incr(" hit_count ");
4 get(" mbbx6spp : repos_count ");
5 }
6 });

31. Automatic Optimal Pipelining
http://informatikr.com/2012/redis-pipelining.html
Listing 25: Pipelining in Jedis
1 jedis . pipelined (new PipelineBlock () {
2 public void execute () {
3 incr(" hit_count ");
4 get(" mbbx6spp : repos_count ");
5 }
6 });
Listing 26: Automatic Pipelining in Hedis
1 runRedis conn $ do
2 hits <- incr " hit_count "
3 repos <- get " mbbx6spp : repos_count "
4 liftIO $ print (hits , repos )

32. Monoids: Other Fun Examples
Log Priorities / Filters in bittorrent
http://jlouisramblings.blogspot.com/2010/02/how-logging-is-performed-in-haskell.html
Associative Alpha Blending
http://lukepalmer.wordpress.com/2010/02/05/associative-alpha-blending/
Writer Monad Accumulator
factorial :: Integer -> Writer (Sum Integer) Integer
Tree in Data.Git module of hit package

33. Monoids: Other Fun Examples
Log Priorities / Filters in bittorrent
http://jlouisramblings.blogspot.com/2010/02/how-logging-is-performed-in-haskell.html
Associative Alpha Blending
http://lukepalmer.wordpress.com/2010/02/05/associative-alpha-blending/
Writer Monad Accumulator
factorial :: Integer -> Writer (Sum Integer) Integer
Tree in Data.Git module of hit package

34. Monoids: Other Fun Examples
Log Priorities / Filters in bittorrent
http://jlouisramblings.blogspot.com/2010/02/how-logging-is-performed-in-haskell.html
Associative Alpha Blending
http://lukepalmer.wordpress.com/2010/02/05/associative-alpha-blending/
Writer Monad Accumulator
factorial :: Integer -> Writer (Sum Integer) Integer
Tree in Data.Git module of hit package

35. Monoids: Other Fun Examples
Log Priorities / Filters in bittorrent
http://jlouisramblings.blogspot.com/2010/02/how-logging-is-performed-in-haskell.html
Associative Alpha Blending
http://lukepalmer.wordpress.com/2010/02/05/associative-alpha-blending/
Writer Monad Accumulator
factorial :: Integer -> Writer (Sum Integer) Integer
Tree in Data.Git module of hit package

36. Monoids: Relationships
Monoid v => Map k v also monoid
All monoids are semigroups
Semigroup is monoid minus identity requirement
All groups are monoids
Monoid is group minus inverse unary operator requirement
Free Structures
Get (money for nothing? and) monoids for free

37. Monoids: Relationships
Monoid v => Map k v also monoid
All monoids are semigroups
Semigroup is monoid minus identity requirement
All groups are monoids
Monoid is group minus inverse unary operator requirement
Free Structures
Get (money for nothing? and) monoids for free

38. Monoids: Relationships
Monoid v => Map k v also monoid
All monoids are semigroups
Semigroup is monoid minus identity requirement
All groups are monoids
Monoid is group minus inverse unary operator requirement
Free Structures
Get (money for nothing? and) monoids for free

39. Monoids: Relationships
Monoid v => Map k v also monoid
All monoids are semigroups
Semigroup is monoid minus identity requirement
All groups are monoids
Monoid is group minus inverse unary operator requirement
Free Structures
Get (money for nothing? and) monoids for free

40. Monoids: Relationships
Monads & Monoids
.

41. Monoids: Relationships
Monads & Monoids
A monad over X is the
.

42. Monoids: Relationships
Monads & Monoids
A monad over X is the
monoid in category of endofunctors of X
.

43. Monoids: Relationships
Monads & Monoids
A monad over X is the
monoid in category of endofunctors of X
with binary operator as composition
(of endofunctors)
.

44. Monoids: Relationships
Monads & Monoids
A monad over X is the
monoid in category of endofunctors of X
with binary operator as composition
(of endofunctors)
and identity being the identity endofunctor.

45. Homework
What is an Endofunctor?

46. Questions?
Figure: http://www.flickr.com/photos/42682395@N04/
@FunAlgebra
@SusanPotter

47. Bonus: References / Resources
Channel 9 Lectures (Erik Meijer)
http://channel9.msdn.com/Shows/Going+Deep/
Lecture-Series-Erik-Meijer-Functional-Programming-Fundamentals-Chapter-1
The Catsters
http://www.youtube.com/thecatsters
Haskell Reddit
http://www.reddit.com/r/haskell/
Haskell Cafe
http://www.haskell.org/mailman/listinfo/haskell-cafe
Scalaz Mailing List
https://groups.google.com/forum/?fromgroups#!forum/scalaz