The document explores the concepts of functors, monoids, and monads, primarily in the context of Haskell and Kotlin programming languages. It outlines the laws governing these structures, provides code examples, and delves into the operational aspects of monads including unit returns and bind operations. Resources for further learning and source code examples are also included.

1. Monads are
no Nomads
By João Esperancinha
2024/10/08
Unlocking the basics

2. Talking Points
● Functors
● Monoids
● Monads

3. Functors
● Mapping function: fmap in Haskell, map in Kotlin
● Functor Laws:
● Identity Law: F<X>.map(::identity) == F<X>
● Composition Law:
F<X>.map(f.compose(g)) == F<X>.map(g).map(f) == F(X).map {g(f(it)}
Sources: https://wiki.haskell.org/Functor

4. Functors
mapping
(functor
mapping)

5. Haskel Example for a Functor (List)
print (fmap addOne (Just 5))
print (fmap addOne Nothing)
print (fmap addOne [1, 2, 3, 4, 5])
print (fmap square [1, 2, 3, 4, 5])
print ([1,2,3,4,5])
print (fmap identityFunction [1,2,3,4,5])
print (fmap (addOne . square) [1,2,3,4,5] == (fmap addOne . fmap square)
[1,2,3,4,5])
addOne :: Int -> Int
addOne x = x + 1
square :: Int -> Int
square x = x * x
identityFunction :: Int -> Int
identityFunction x = x
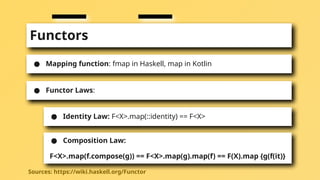
Identity law
Compositio
n
Mapping
function

6. Kotlin Example for a Functor (List)
treeCollection.map { it } shouldBe treeCollection
}
val treeCollection = (1..10)
.map { Tree((1..10).map { Leaf() }) } Identity Law

7. Kotlin Example for a Functor (List)
val f: (Tree) -> Tree = { Tree(leaves = (1..5).map { Leaf(color = Color.BLUE) }) }
val g: (Tree) -> Tree = { Tree(leaves = (1..6).map { Leaf(color = Color.BLACK) }) }
treeCollection.map(g.compose(f)) shouldBe treeCollection.map(f).map(g)
treeCollection.map(f).map(g).shouldForAll {
it.leaves.shouldForAll { it.color shouldBe Color.BLACK }
}
val treeCollection = (1..10)
.map { Tree((1..10).map { Leaf() }) }
Compositio
n
Mapping
function
Mapping
function
Function
s

8. Monoids (M, *), a set M with binary
operation *
● Closure: For every a and b in domain M, the result of a * b is also in
domain M.
● Associativity: For every a and b and z in M, (a * b) * z = a * (b * z)
● Identity: There is one element i in M, such that for all a in M, i * a = a * i
= a.
Sources: https://userpages.cs.umbc.edu/artola/studyaids/AbstractAlgebraPrimer.pdf

9. Monoids

10. Haskel Example for a Monoid (List)
let list1 = [1, 2, 3]
list2 = [4, 5, 6]
combinedList = list1 <> list2
list1Empty = list1 <> mempty
list2Empty = mempty <> list2
putStrLn $ "List 1: " ++ show list1
putStrLn $ "List 2: " ++ show list2
putStrLn $ "List 1 with empty: " ++ show list1Empty
putStrLn $ "List 2 with empty: " ++ show list2Empty
putStrLn $ "Combined List: " ++ show combinedList
putStrLn $ "Identity: " ++ show (mempty :: [Int])
putStrLn $ "Associativity 1: " ++ show ((list1 <> list2) <> list1)
putStrLn $ "Associativity 2: " ++ show (list1 <> (list2 <> list1))
Associativit
y
Identity
Closure
Binary
Operator

11. Kotlin Example for a Monoid (List)
(treeCollection + emptyList) shouldBe (emptyList + treeCollection)
(emptyList + treeCollection) shouldBe treeCollection
(treeCollection1.shouldBeTypeOf<ArrayList<Tree>>() +
treeCollection.shouldBeTypeOf<ArrayList<Tree>>())
.shouldBeTypeOf<ArrayList<Tree>>() shouldHaveSize 12
((treeCollectionA + treeCollectionB) + treeCollectionC) shouldBe
(treeCollectionA + (treeCollectionB + treeCollectionC))
Associativit
y
Identity
Closure
Binary
Operator

12. Monads
● Type constructor (i.e. List<T> in Kotlin where T is a constructor)
● Unit or monadic return: return :: a -> M a, also listOf in Kotlin
● Bind operator: (>>=) :: M a -> (a -> M b) -> M b, also flatMap in Kotlin
Sources: https://www.dcc.fc.up.pt/~pbv/aulas/tapf/handouts/monads.html
● Left Identity Law: return a >>= f = f a, or in Kotlin listOf(tree1).flatMap(f) shouldBe
f(tree1)
● Right Identity Law: M a >>= return = M a, or in Kotlin trees.flatMap { listOf(it) }
shouldBe trees
● Associativity: (M a >>= f) >>= g = M a >>= (x -> f x >>= g), or inKotin
trees.flatMap(f).flatMap(g) shouldBe trees.flatMap { x -> f(x).flatMap(g) }

13. Monads
flatMap
(bind)

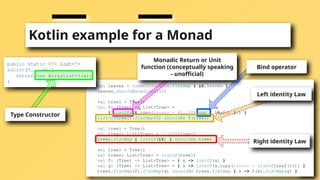
14. Haskell example for a Monad
createTwoElementFunction :: Int -> [Int]
createTwoElementFunction x = [x, x + 1]
createDoubleElementFunction :: Int -> [Int]
createDoubleElementFunction x = [x * 2]
leftIdentityTest :: Int -> Bool
leftIdentityTest a = (return a >>= createTwoElementFunction) == createTwoElementFunction a
rightIdentityTest :: [Int] -> Bool
rightIdentityTest m = (m >>= return) == m
associativityTest :: [Int] -> Bool
associativityTest m = ((m >>= createTwoElementFunction) >>= createDoubleElementFunction) ==
(m >>= (x -> createTwoElementFunction x >>= createDoubleElementFunction))
main :: IO ()
main = do
let testValue :: Int
testValue = 5
let testList :: [Int]
testList = [1,2,3]
let listOfLists :: [[Int]]
listOfLists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
putStrLn $ "Used the unit operation (" ++ show (return testValue :: [Int]) ++ "): "
putStrLn $ "Just a flatMap operation (" ++ show testList ++ "): " ++ show (testList >>= (x -> [x * 2]))
putStrLn $ "Another flatMap operation (" ++ show listOfLists ++ "): " ++ show (listOfLists >>= (x -> x))
putStrLn $ "Left Identity (" ++ show testValue ++ "): " ++ show (leftIdentityTest testValue)
putStrLn $ "Right Identity (" ++ show testList ++ "): " ++ show (rightIdentityTest testList)
putStrLn $ "Associativity (" ++ show testList ++ "): " ++ show (associativityTest testList)
Type Constructor
Monadic Return
Bind operator
Left identity Law
Right identity Law
Associativity Law

15. Kotlin example for a Monad
val leaves = treeCollection.flatMap { it.leaves }
leaves.shouldHaveSize(100)
val tree1 = Tree()
val f: (Tree) -> List<Tree> =
{ listOf(it.copy(leaves = (1..10).map { Leaf() })) }
listOf(tree1).flatMap(f) shouldBe f(tree1)
val tree1 = Tree()
val trees: List<Tree> = listOf(tree1)
trees.flatMap { listOf(it) } shouldBe trees
val tree1 = Tree()
val trees: List<Tree> = listOf(tree1)
val f: (Tree) -> List<Tree> = { x -> listOf(x) }
val g: (Tree) -> List<Tree> = { x -> listOf(x.copy(leaves = listOf(Leaf()))) }
trees.flatMap(f).flatMap(g) shouldBe trees.flatMap { x -> f(x).flatMap(g) }
public static <T> List<T>
asList(T... a) {
return new ArrayList<>(a);
}
Type Constructor
Monadic Return or Unit
function (conceptually speaking
- unofficial)
Bind operator
Left identity Law
Right identity Law

16. Questions?
I am an inquisitive
cat

17. Resources
Online
● https://wiki.haskell.org/Functor
● https://www.dcc.fc.up.pt/~pbv/aulas/tapf/handouts/monads.html
● https://www.oreilly.com/library/view/learning-functional-programming/9781787281394/84ae03df-fe
b2-4fd6-925b-728a95ed04de.xhtml
● https://userpages.cs.umbc.edu/artola/studyaids/AbstractAlgebraPrimer.pdf
Slides available:

18. Source code and documentation
● https://github.com/jesperancinha/jeorg-kotlin-test-drives (Source code with Kotlin examples)
● https://github.com/jesperancinha/haskell-test-drives (Source code with Haskell examples)

19. About me
● Homepage - https://joaofilipesabinoesperancinha.nl
● LinkedIn - https://www.linkedin.com/in/joaoesperancinha/
● YouTube - JESPROTECH
■ https://www.youtube.com/channel/UCzS_JK7QsZ7ZH-zTc5kBX_g
■ https://www.youtube.com/@jesprotech
● Bluesky - https://bsky.app/profile/jesperancinha.bsky.social
● Mastodon - https://masto.ai/@jesperancinha
● GitHub - https://github.com/jesperancinha
● Hackernoon - https://hackernoon.com/u/jesperancinha
● DevTO - https://dev.to/jofisaes
● Medium - https://medium.com/@jofisaes

20. Thank you!
By João Esperancinha
2024/10/08
Monads
are no
Nomads