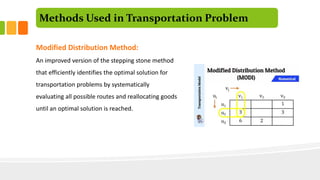
The document discusses the transportation problem, which involves optimizing the distribution of goods from multiple sources to multiple destinations to minimize total transportation costs while meeting supply and demand constraints. It outlines various types of transportation problems, such as balanced and unbalanced issues, and methods used for solving these problems, including the north-west corner method and Vogel's approximation method. The transportation problem has widespread applications in logistics and supply chain management, emphasizing its importance in efficient resource allocation.