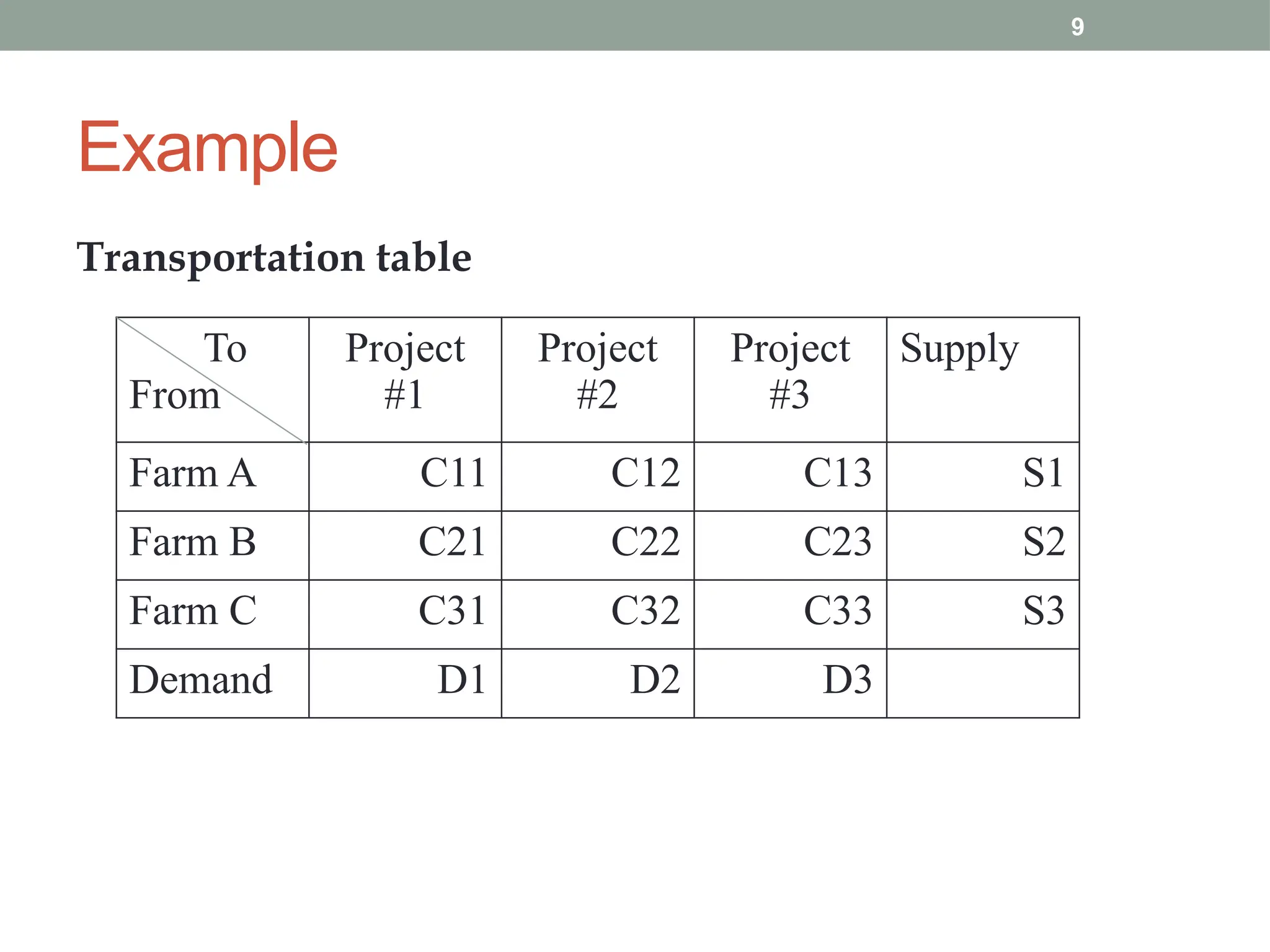
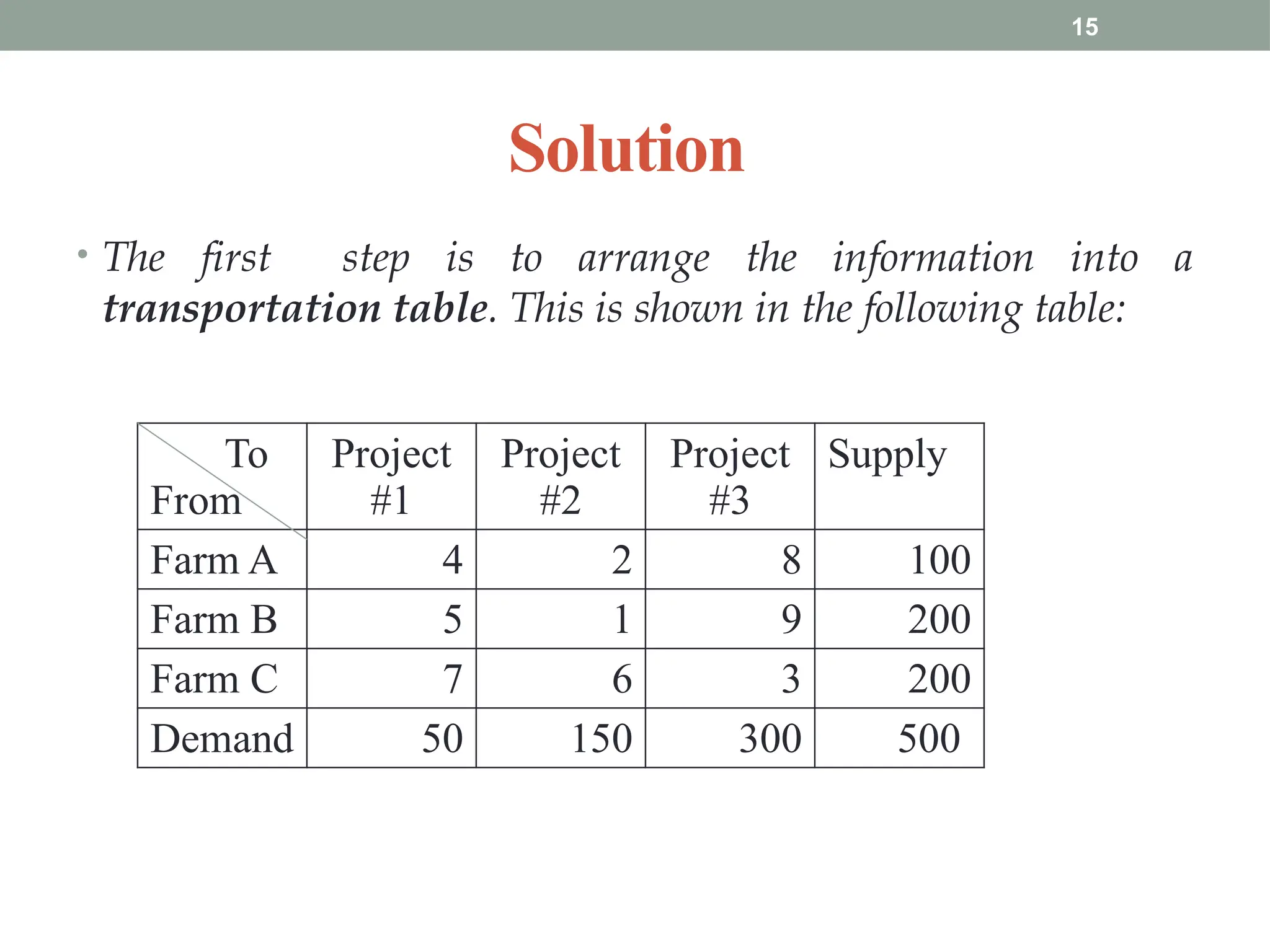
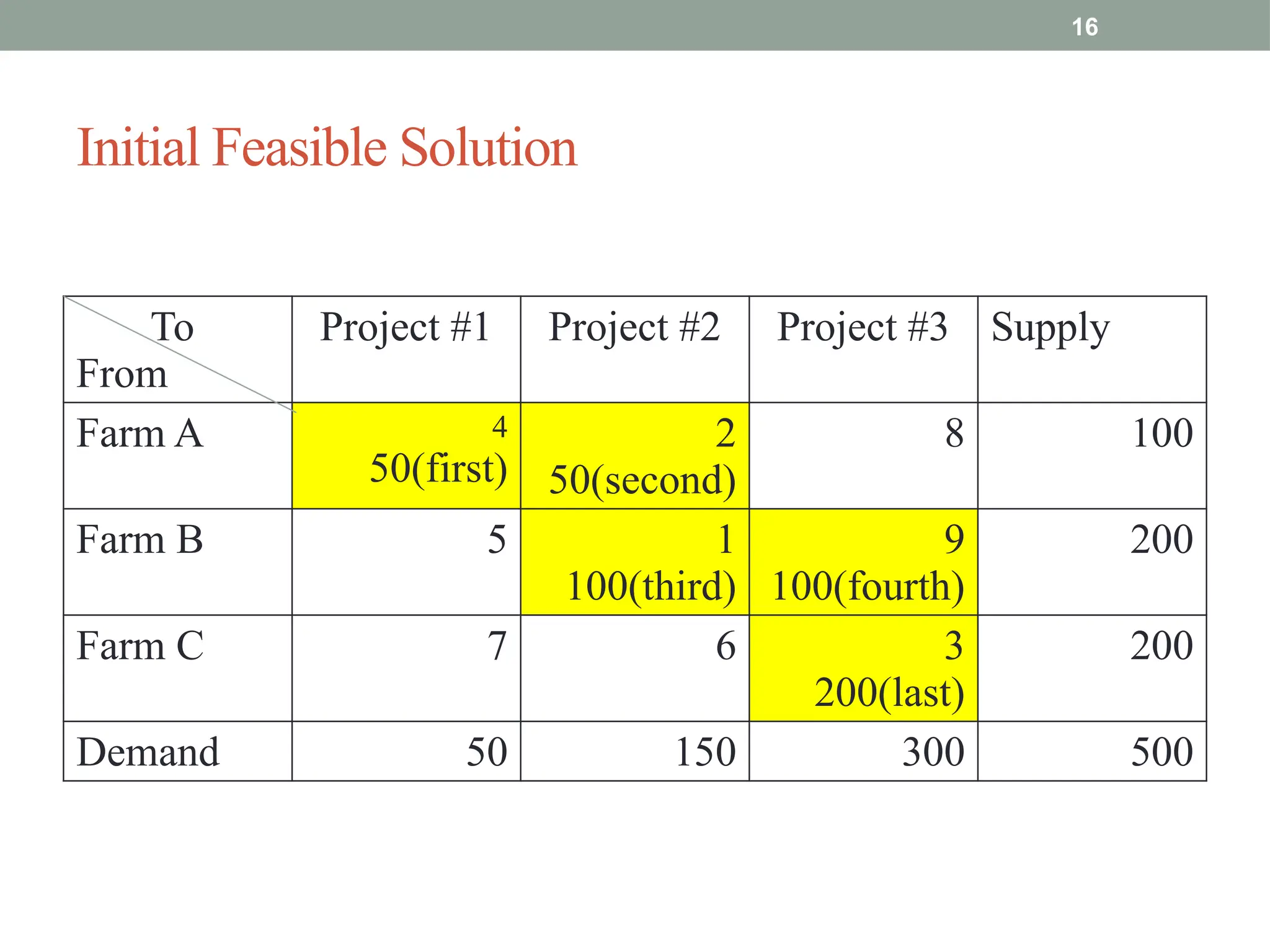
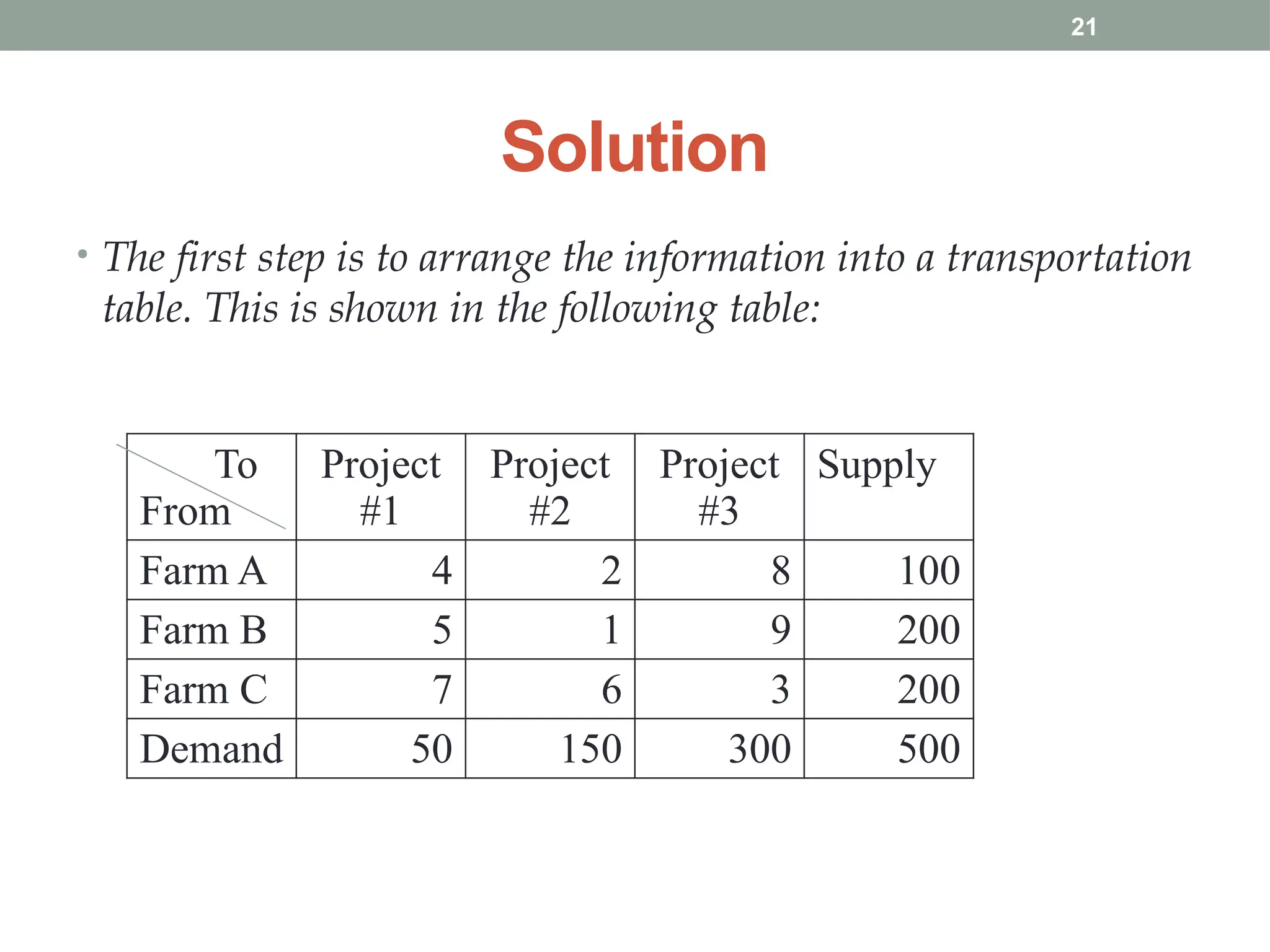
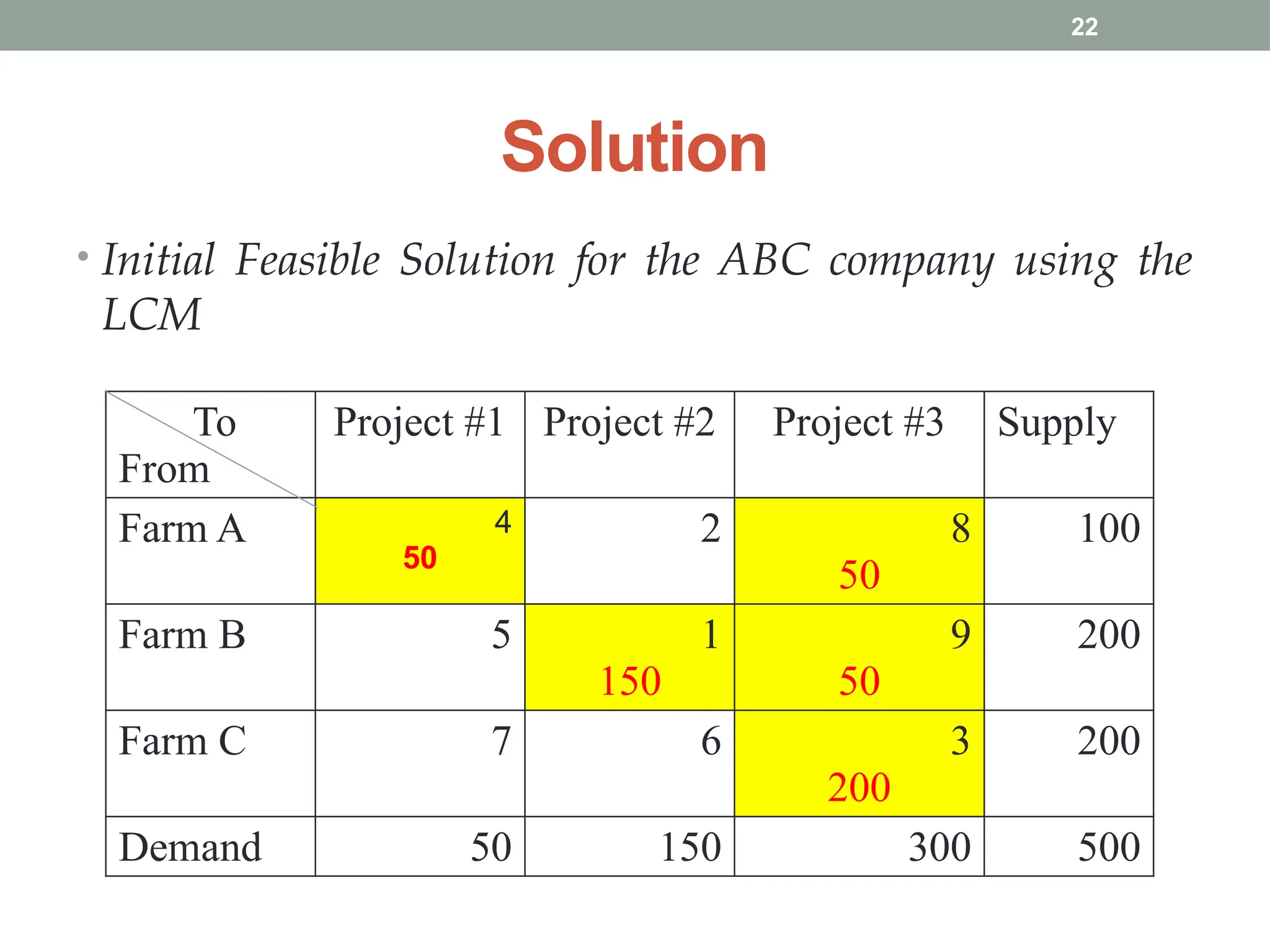
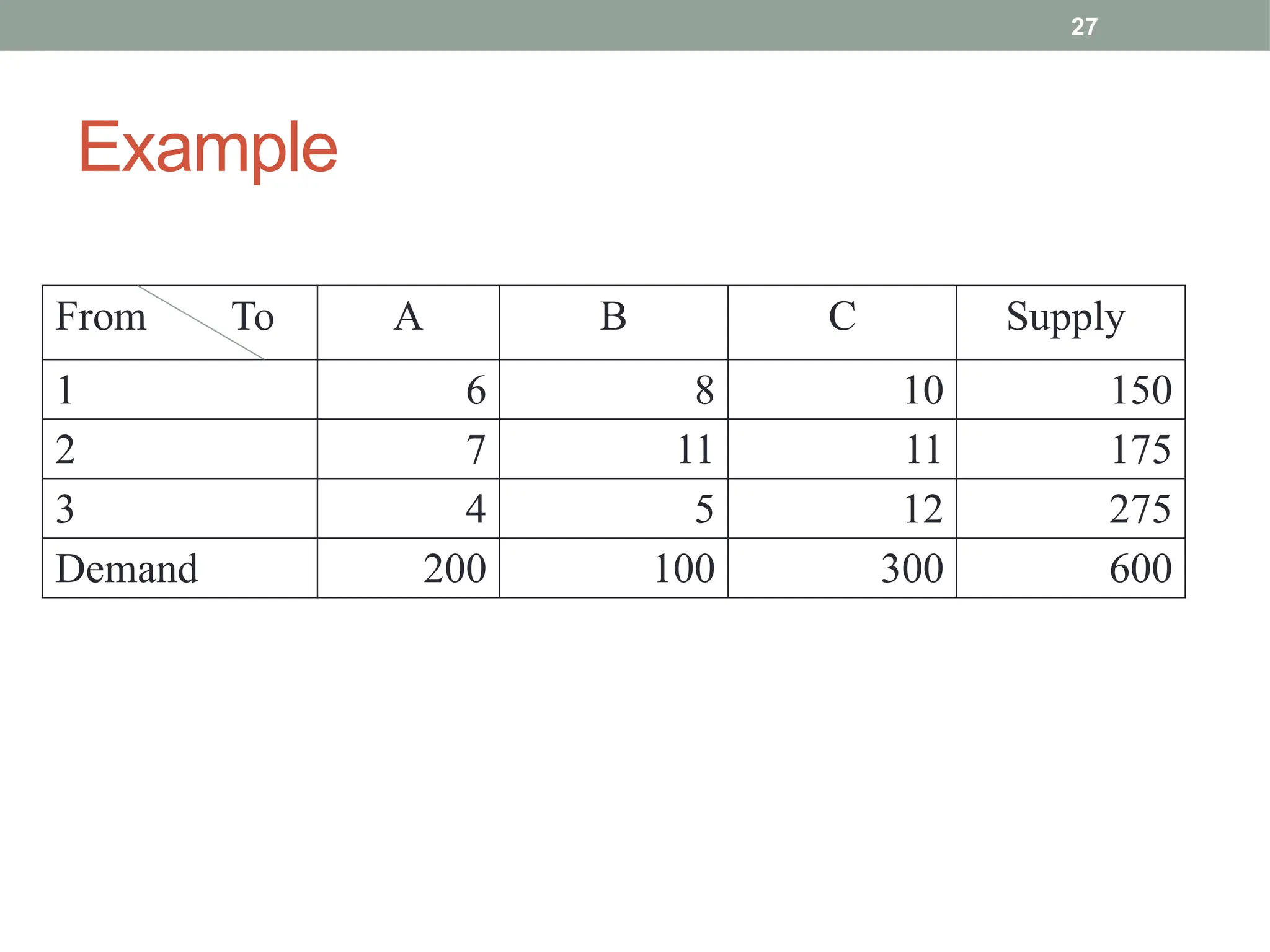
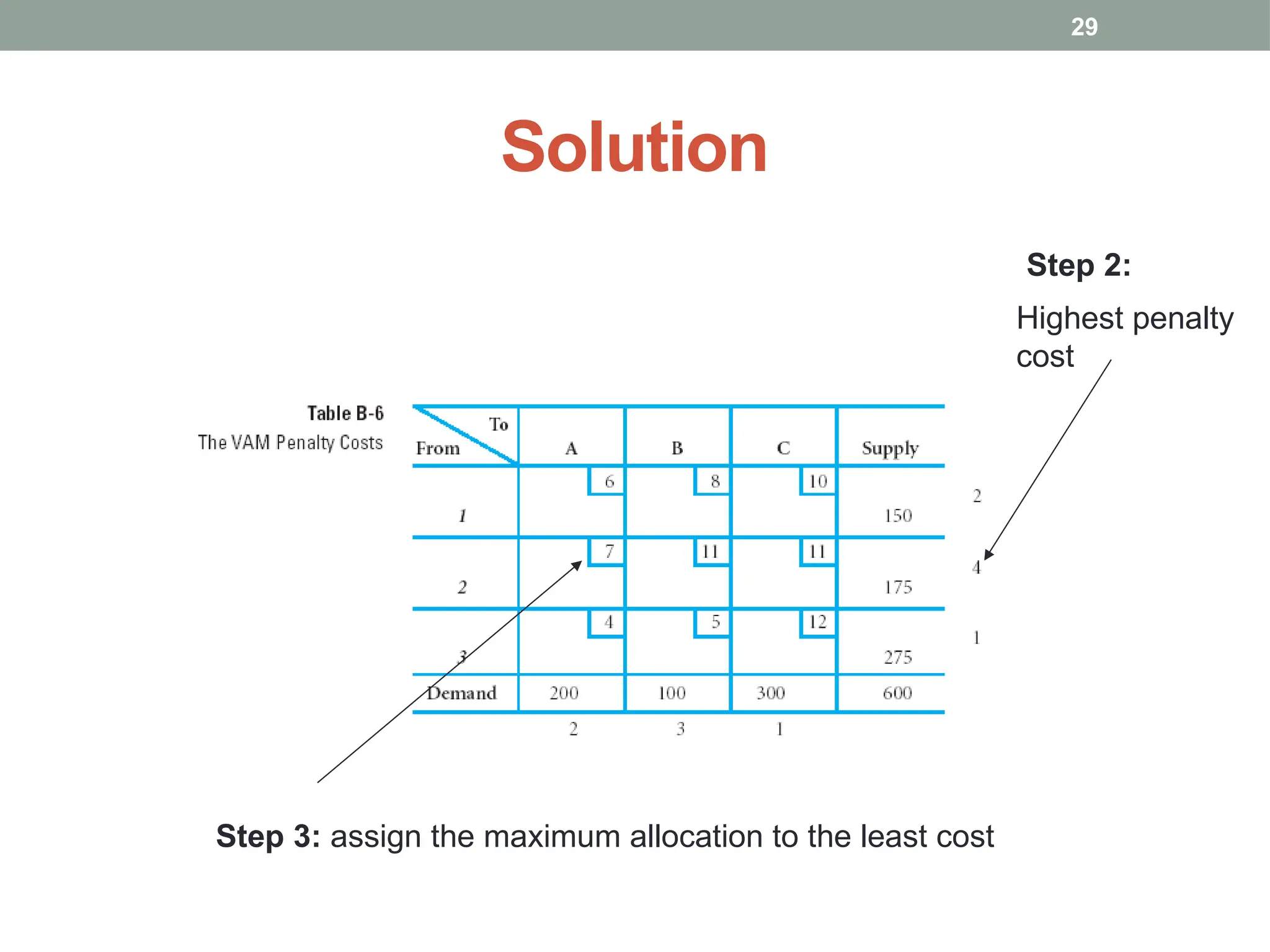
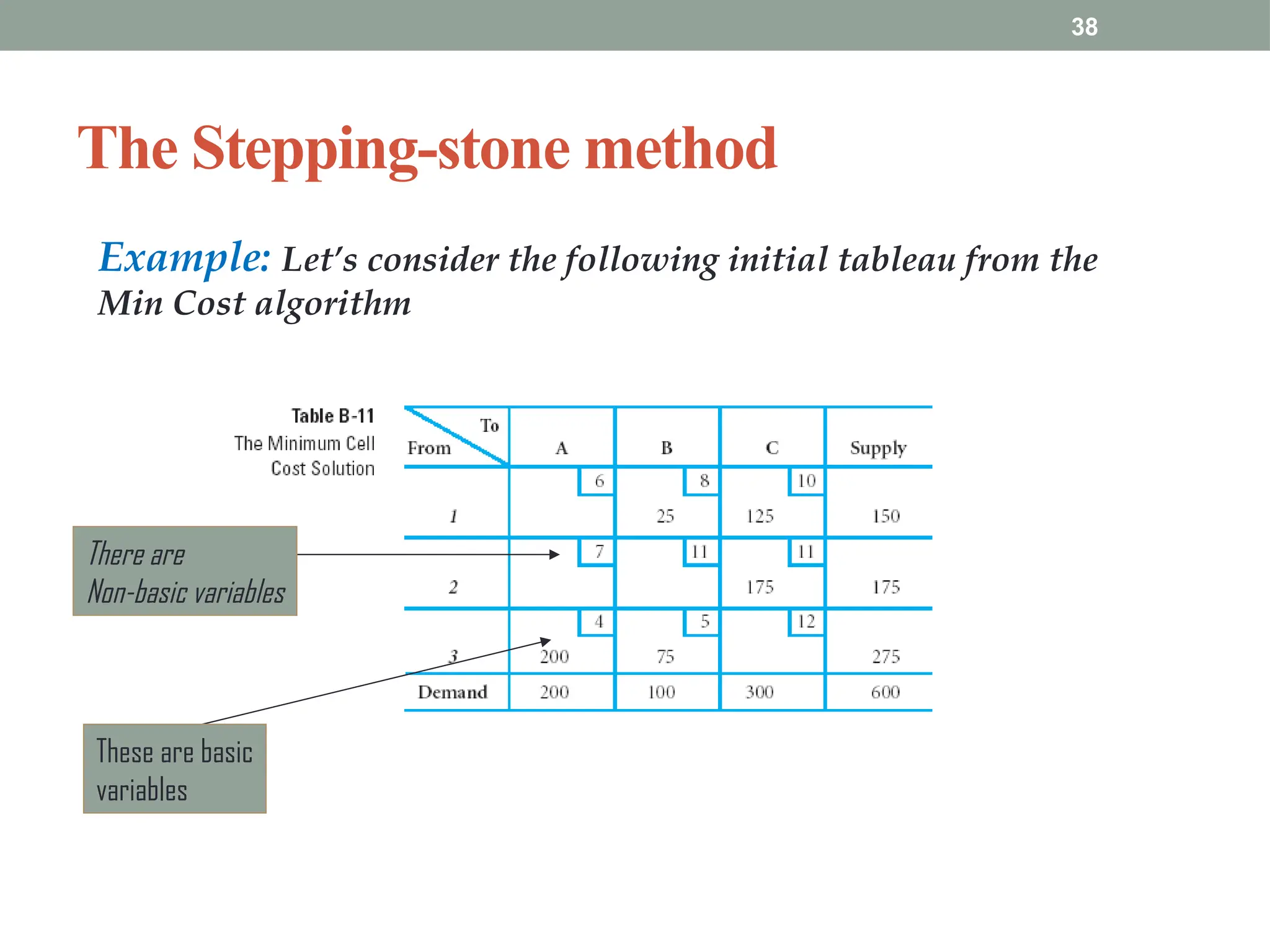
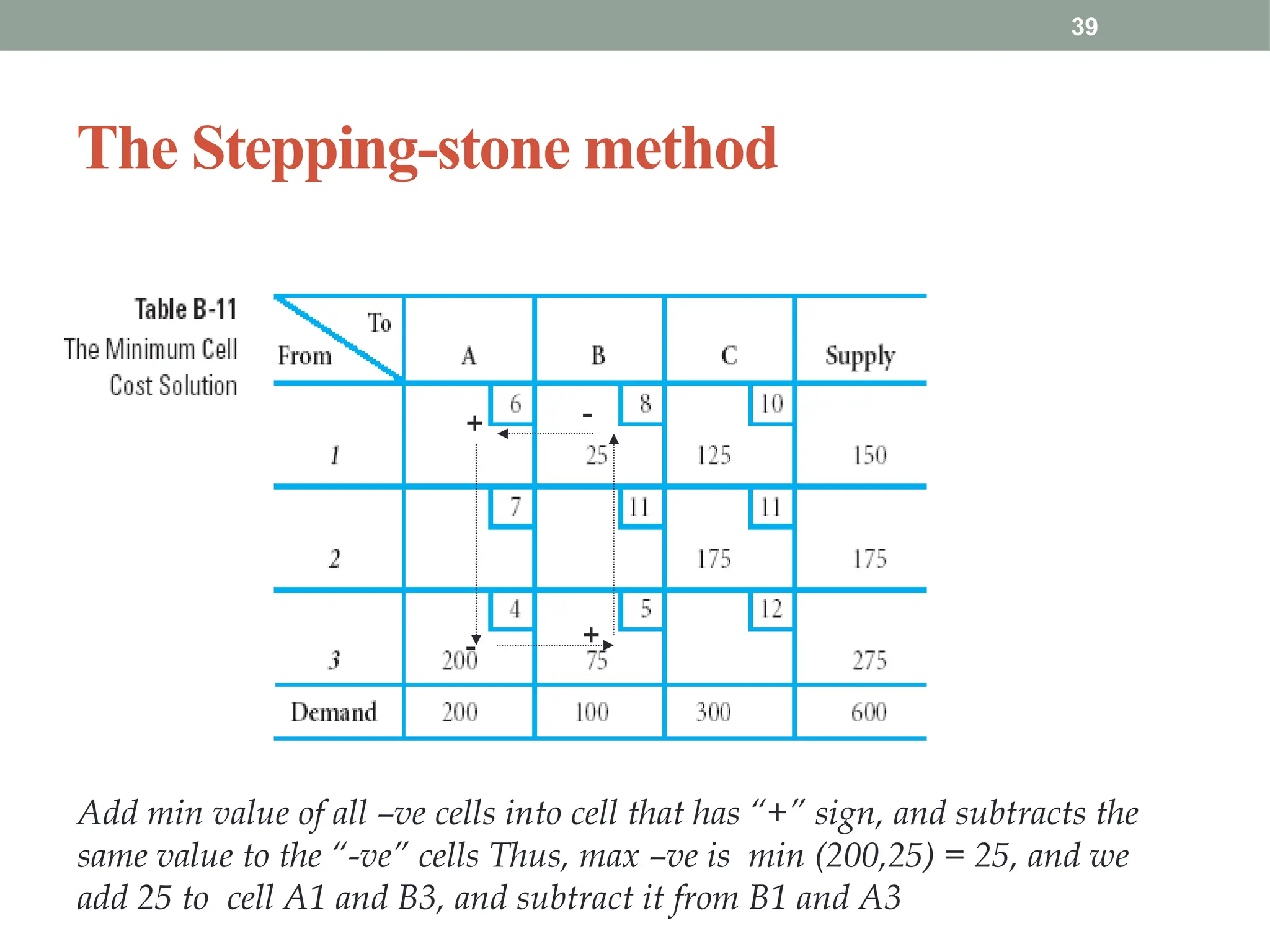
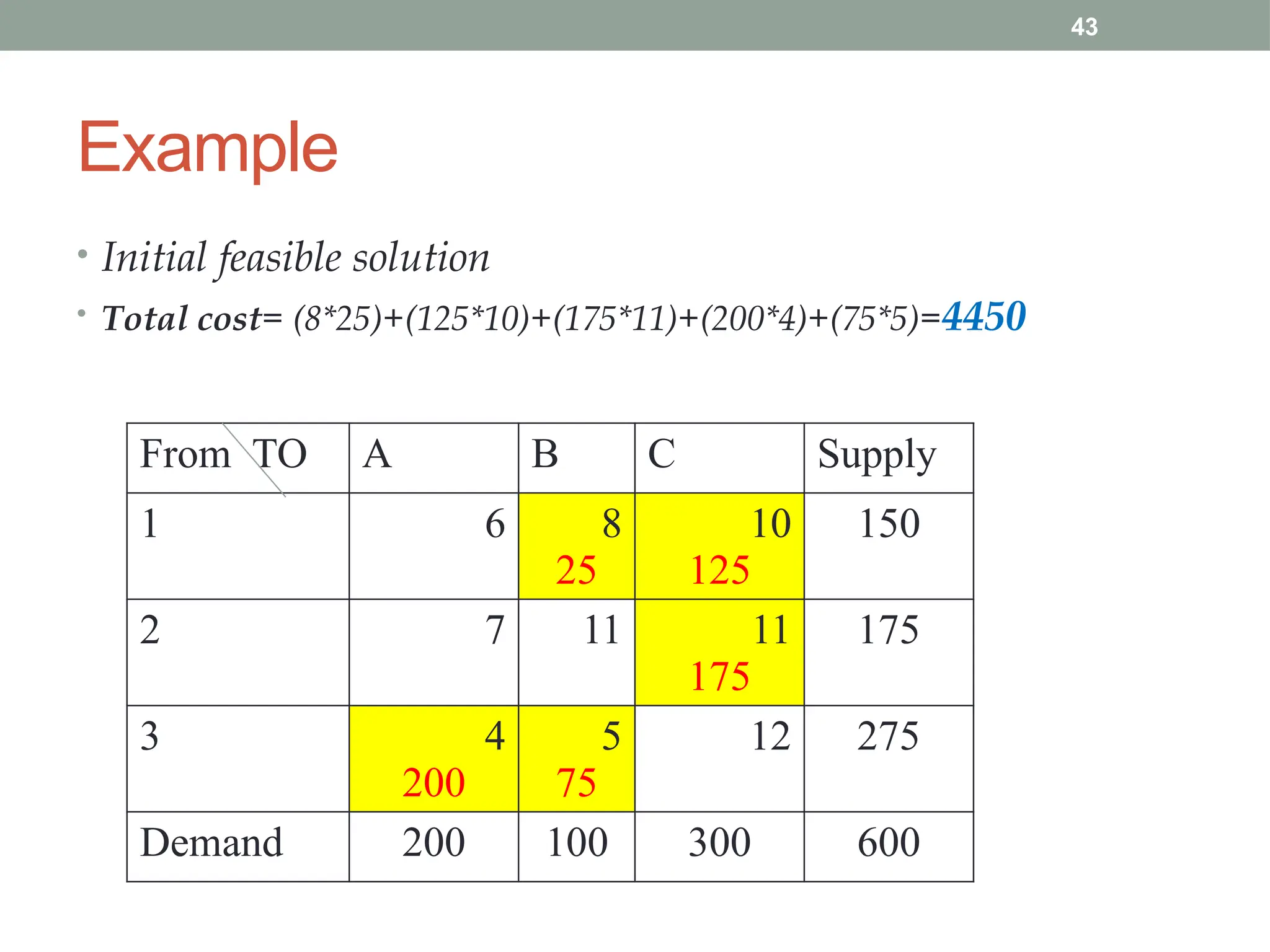
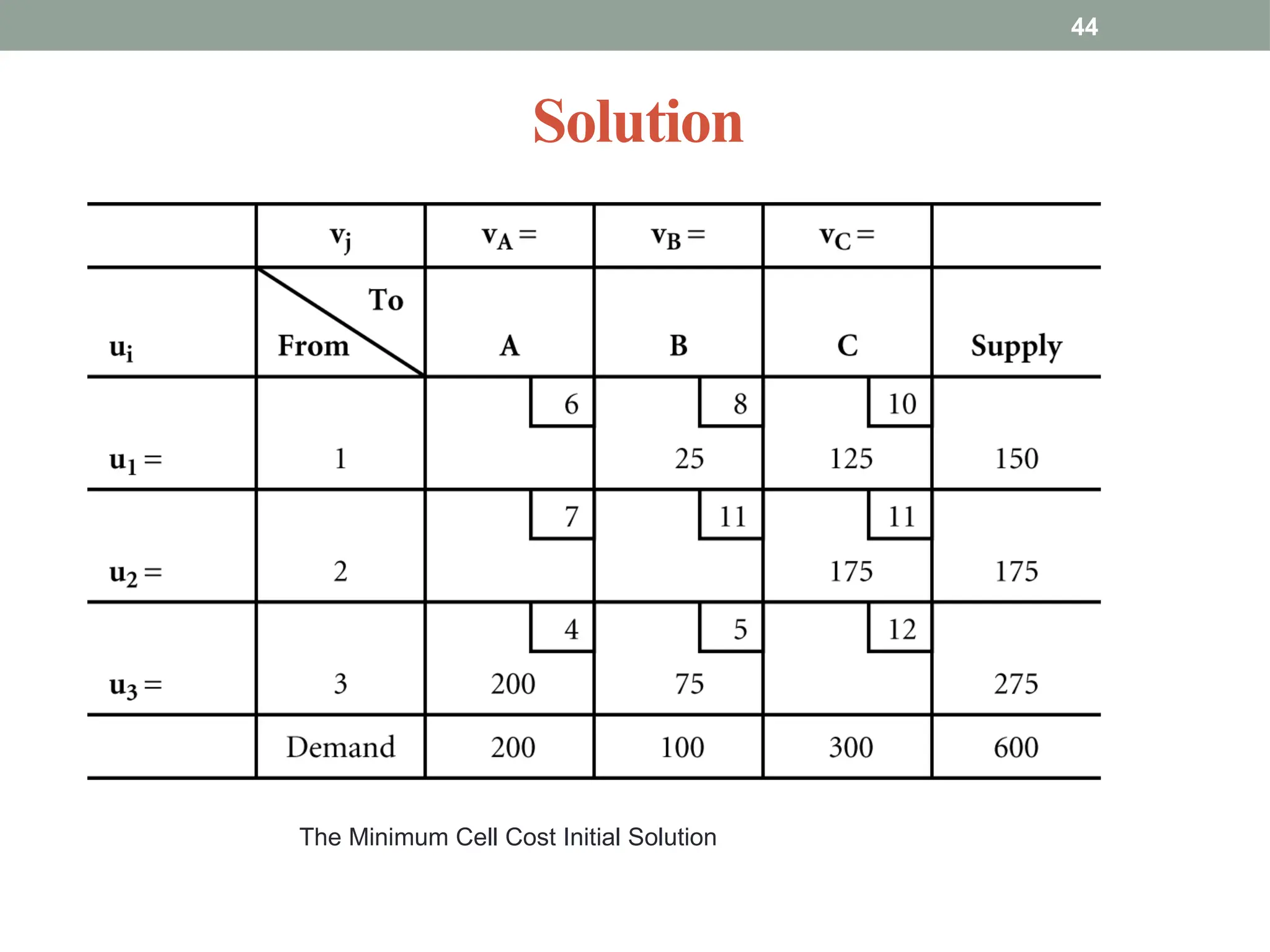
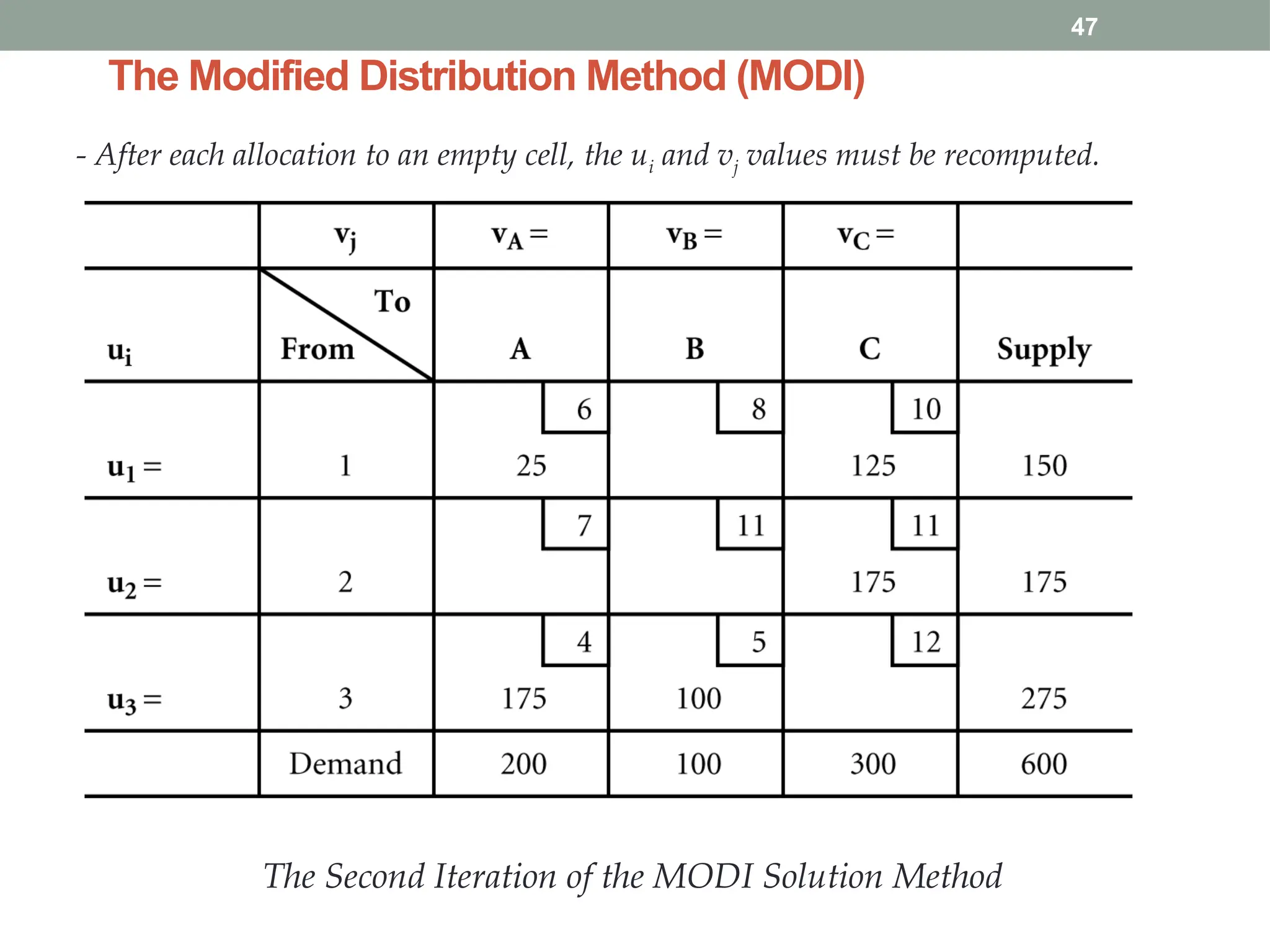
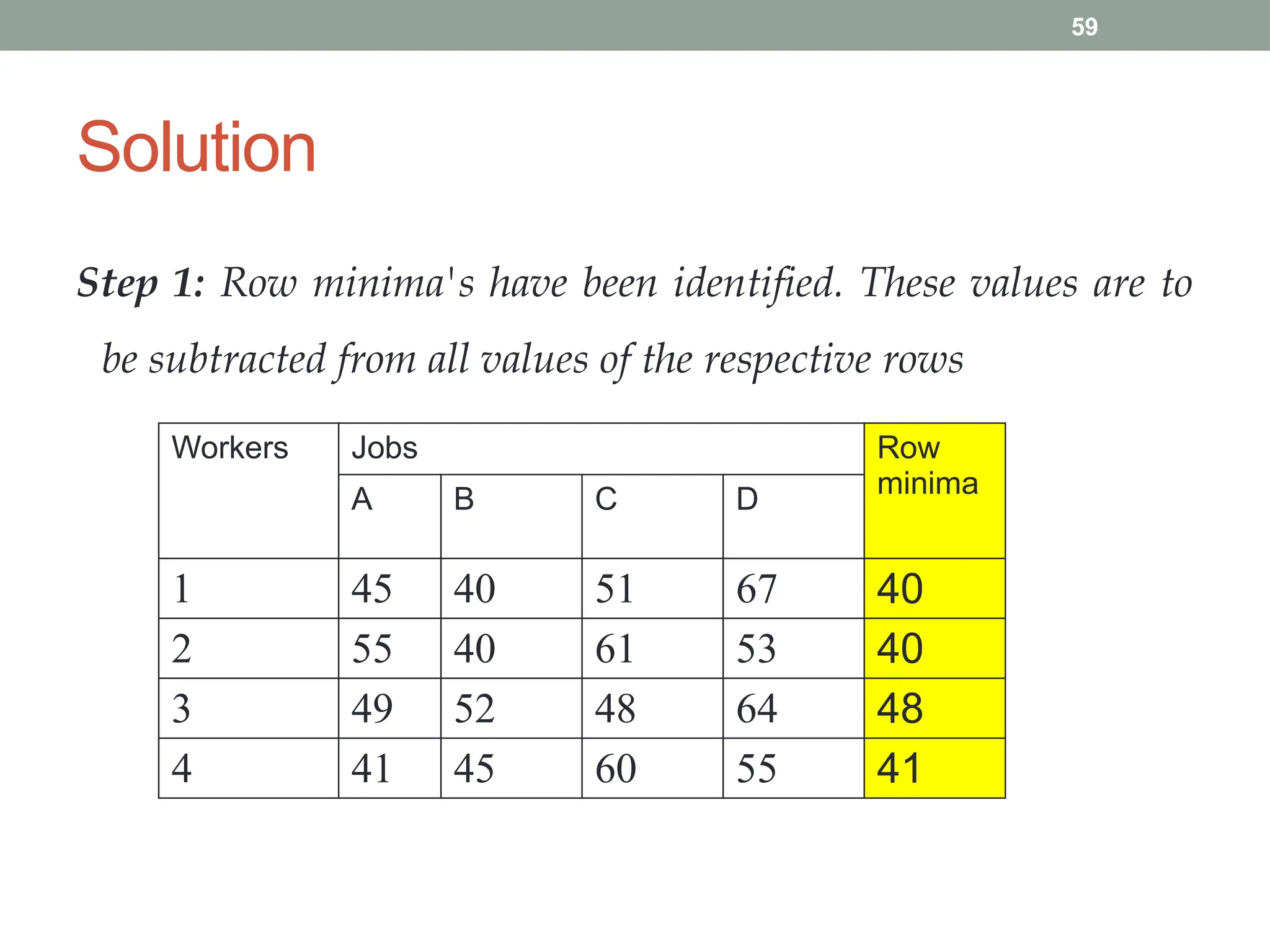
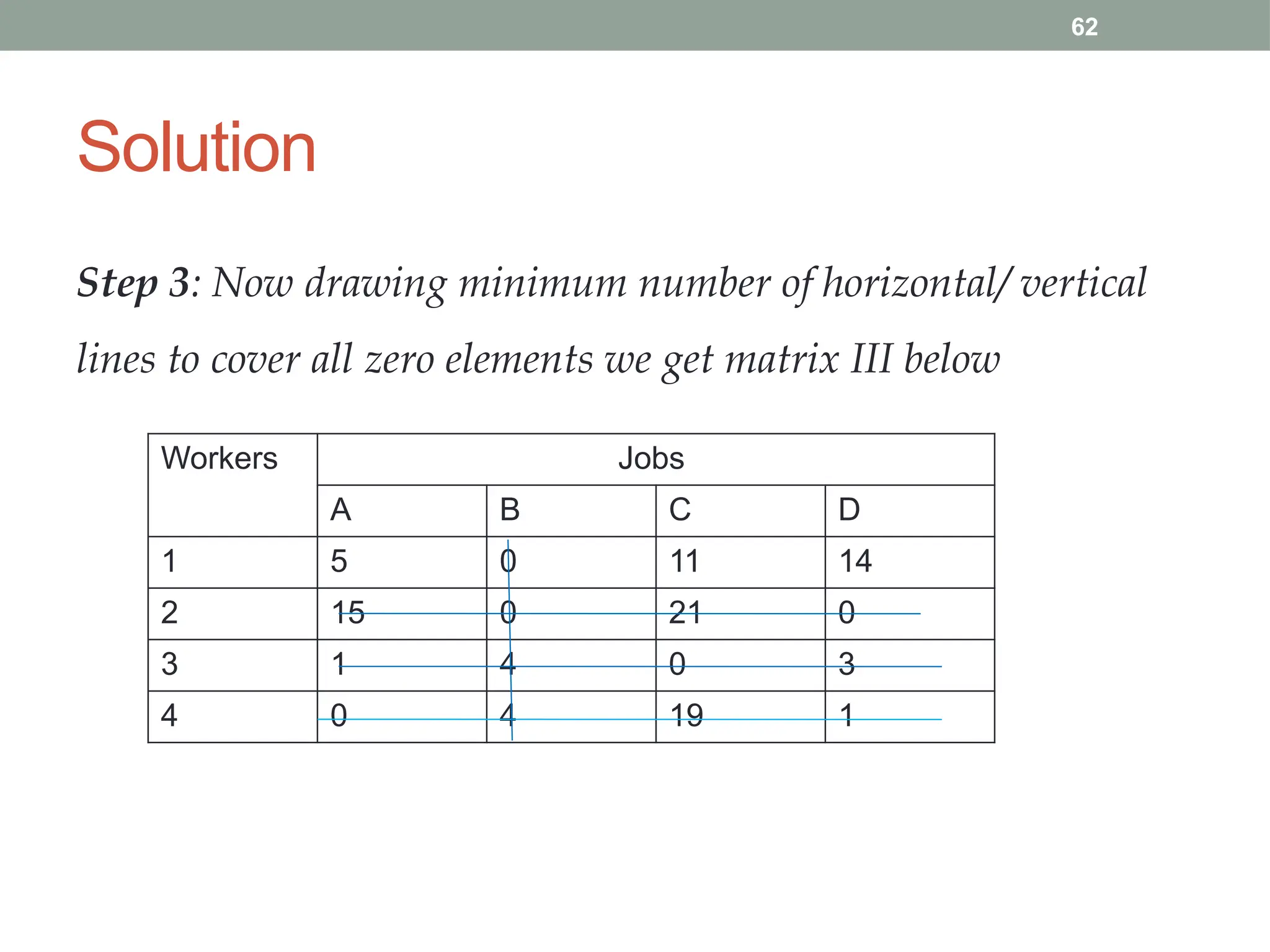
Transportation and Assignment Problems are special types of linear programming problems used in operations research. The transportation problem focuses on finding the most cost-effective way to distribute goods from multiple sources (like factories) to multiple destinations (like warehouses) while satisfying supply and demand constraints. Common solution methods include the North-West Corner Rule, Least Cost Method, and Vogel’s Approximation Method, followed by optimization using the MODI method. The assignment problem involves assigning tasks or resources (e.g., workers to jobs) in a way that minimizes cost or time or maximizes efficiency. It is typically solved using the Hungarian Method, ensuring that each task is assigned to only one agent. These problems are widely used in logistics, scheduling, and resource allocation.