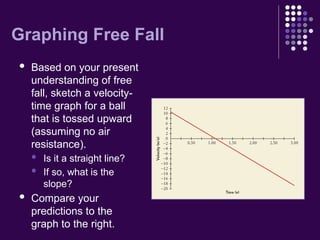
The document discusses the concept of free fall in one dimension, assuming no air resistance, with a constant acceleration of -9.8 m/s² due to gravity. It includes examples and practice problems involving calculating velocity, displacement, and height related to free fall scenarios. The document also contains guidelines for sketching motion graphs and making predictions based on initial conditions.