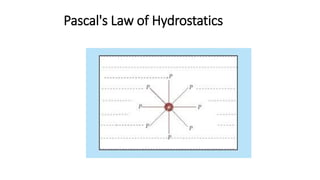
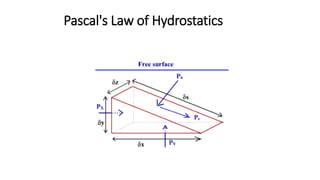
The document focuses on fluid statics, specifically hydrostatics, which studies fluids at rest and has various applications, including buoyancy measurements and density calculations. It introduces concepts of fluid elements, body forces, and surface forces, highlighting Pascal's law which states that normal stresses in a fluid at rest are equal in all directions. The document also outlines the basic equations of fluid statics and conditions under which they are valid, emphasizing static fluids and gravitational force.