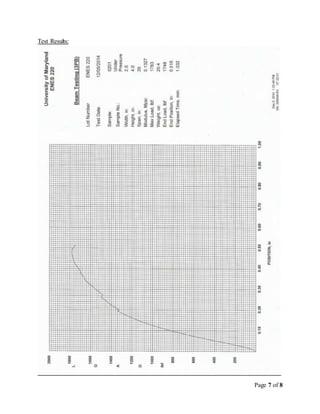
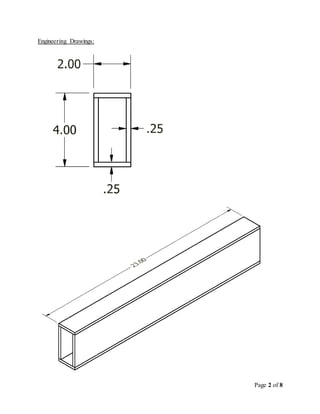
The team designed and tested a wooden beam to hold between 1000-2000 pounds. They calculated stresses and deflections, predicting the beam would fail by glue shear above 3500 pounds. During testing, the beam failed at 1783 pounds due to an unexpected flange crack in the top plate. While the failure load was in the target range, it was lower than predicted. To improve the design, the team recommends a cross-section shape less prone to flange cracks, like an I-beam with double webs.

1. Beam Design Final Report
Team Under Pressure
ENES220 Section 0201
Dr. Bowden
David Hairumian, Mitchell McNamara, Daniel Pedraza, Nick Seiler
12/12/2014

2. Page 1 of 8
Table of Contents:
Introduction
Material Properties
Engineering Drawings
Shear-Moment Diagrams
Centroid and Moment of Inertia Calculations
Beam Stress Calculations
Glue Stress Calculations
Deflection Calculations
Predictions
Test Results
Discussion of Results
Conclusions and Recommendations
1
1
2
3
4
4
5
5
6
7
8
8
Introduction:
Our objective for this project was to build a beam that would hold between 1000 and
2000 pounds while demonstrating the highest strength-to-weight ratio. First, we came up with a
series of potential cross sections and calculated the material stresses in each cross section. Using
data gathered from material testing, we decided on a box beam made from poplar and held
together with Elmer’s wood glue. After constructing the beam, we tested it in a three-point
bending setup and collected data as the applied force was increased until failure.
Material Properties:
Poplar Tensile Strength (psi) Shear Strength (psi)
Average: 15,478 2,265
Maximum: 18,000 2,850
Minimum: 13,800 2,090
Elmer’s
on Poplar
Shear Strength (psi)
Average: 1,122
Maximum: 1,374
Minimum: 1,054

3. Page 2 of 8
Engineering Drawings:

4. Page 3 of 8
Shear-Moment Diagrams:
-1000
-800
-600
-400
-200
0
200
400
600
800
0 5 10 15 20 25
V(lb)
x (in)
Shear Diagram
600
-900
0
1000
2000
3000
4000
5000
6000
7000
8000
0 5 10 15 20 25
M(lb-in)
x (in)
Moment Diagram
7200

5. Page 4 of 8
Centroid and Moment of Inertia:
Centroid Location: 𝑥̅ = 1𝑖𝑛, 𝑦̅ = 2 𝑖𝑛 (by symmetry)
Moment of Inertia: 𝐼 =
1
12
[ 𝑏ℎ3] =
1
12
[(2𝑖𝑛)(4𝑖𝑛)3] = 5.3073 𝑖𝑛4
Beam Stresses:
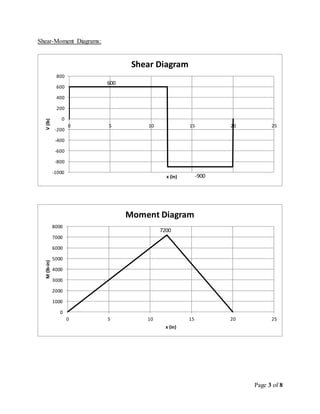
From V-M Diagrams: 𝑉𝑚𝑎𝑥 = 900𝑙𝑏, 𝑀 𝑚𝑎𝑥 = 7200𝑙𝑏 ∙ 𝑖𝑛
Normal Stress: 𝜎 𝑚𝑎𝑥 =
𝑀 𝑚𝑎𝑥 𝑐
𝐼
=
(7200𝑙𝑏∙𝑖𝑛)(2𝑖𝑛)
5.3073𝑖 𝑛4 = 2713.2 𝑝𝑠𝑖
Shear Stress: 𝜏 𝑚𝑎𝑥 =
𝑉 𝑚𝑎𝑥 𝑄
𝐼𝑡
𝑄 = 𝐴∗
𝑦̅∗
𝐴∗
= (2𝑖𝑛)(2𝑖𝑛) − (1.5𝑖𝑛)(1.75𝑖𝑛) = 1.375 𝑖𝑛2
𝑦̅∗
=
(4𝑖 𝑛2)(2𝑖𝑛)−(2.625𝑖 𝑛2 )(.875𝑖𝑛 )
4𝑖 𝑛2 −2.625𝑖 𝑛2 = 1.2386 𝑖𝑛
𝜏 𝑚𝑎𝑥 =
(900𝑙𝑏)(1.375𝑖 𝑛2 )(1.2386𝑖𝑛)
(5.3073𝑖 𝑛4)(0.5𝑖𝑛 )
= 577.61 𝑝𝑠𝑖
Safety Factors:
Normal: 𝜎𝑎𝑙𝑙𝑜𝑤 = 13,800 𝑝𝑠𝑖
𝑆. 𝐹. =
𝜎 𝑎𝑙𝑙𝑜𝑤
𝜎 𝑚𝑎𝑥
=
13,800𝑝𝑠𝑖
2,713.2𝑝𝑠𝑖
= 5.086
Shear: 𝜏 𝑎𝑙𝑙𝑜𝑤 = 2,090 𝑝𝑠𝑖
𝑆. 𝐹. =
𝜏 𝑎𝑙𝑙𝑜𝑤
𝜏 𝑚𝑎𝑥
=
2,090𝑝𝑠𝑖
577.61𝑝𝑠𝑖
= 3.618

6. Page 5 of 8
Glue Stress:
Shear Stress: 𝜏𝑔𝑙𝑢𝑒 =
𝑞
𝑁𝑤
, 𝑞 =
𝑉 𝑚𝑎 𝑥 𝑄
𝐼
𝑄 = 𝐴∗
𝑦̅∗
𝐴∗
= (2𝑖𝑛)(0.25𝑖𝑛) = 0.5 𝑖𝑛2
𝑦̅∗
= 2𝑖𝑛 − (
0.25𝑖𝑛
2
) = 1.875 𝑖𝑛2
𝑞 =
(900𝑙𝑏)(0.5𝑖 𝑛2)(1.875𝑖𝑛)
5.3073𝑖 𝑛4 = 158.99 𝑙𝑏/𝑖𝑛
𝜏𝑔𝑙𝑢𝑒 =
158.99𝑙𝑏/𝑖𝑛
2(.25𝑖𝑛 )
= 317.96 𝑝𝑠𝑖
Safety Factor:
Shear: 𝜏 𝑎𝑙𝑙𝑜𝑤 = 760 𝑝𝑠𝑖
𝑆. 𝐹. =
𝜏 𝑎𝑙𝑙𝑜𝑤
𝜏 𝑚𝑎𝑥
=
760𝑝𝑠𝑖
317.96𝑝𝑠𝑖
= 2.390
Deflection:
𝑀( 𝑥) = 𝐹𝐴 < 𝑥 − 0 >1
− 𝑃 < 𝑥 − 12 >1
+ 𝐹𝐵 < 𝑥 − 20 >1
𝐸𝐼𝑦′( 𝑥) =
𝐹 𝐴
2
𝑥2
−
𝑃
2
< 𝑥 − 12 >2
+ 𝐶1
𝐸𝐼𝑦( 𝑥) =
𝐹 𝐴
6
𝑥3
−
𝑃
6
< 𝑥 − 12 >3
+ 𝐶1 𝑥 + 𝐶2
𝐸 = 1.580 ∗ 106
𝑝𝑠𝑖
Boundary Conditions: 𝑦(0) = 0, 𝑦(20) = 0
Solve for Constants 𝐶1 and 𝐶2
𝑦(0) = 0
0 =
600
6
(0)3
−
1500
6
(0)3
+ 𝐶1(0)+ 𝐶2
𝐶2 = 0
𝑦(20) = 0
0 =
600
6
(20)3
−
1500
6
(20 − 12)3
+ 𝐶1(20)
𝐶1 = −33600 𝑙𝑏 ∙ 𝑖𝑛2
Solve for location where slope equals zero:
0 ≤ 𝑥 ≤ 12
0 =
600
2
𝑥2
−
1500
2
(0)2
− 33600
𝑥 = 10.58 𝑖𝑛
12 < 𝑥 ≤ 20
0 =
600
2
𝑥2
−
1500
2
( 𝑥 − 12)2
− 33600
𝑥 = 10.76 𝑖𝑛, 29.24 𝑖𝑛 (𝑛𝑜𝑡 𝑖𝑛 𝑑𝑜𝑚𝑎𝑖𝑛)
Solve for max deflection:
𝑦 𝑚𝑎𝑥 =
1
𝐸𝐼
[
𝐹 𝐴
6
𝑥3
−
𝑃
6
< 𝑥 − 12 >3
− 33600]
𝑦 𝑚𝑎𝑥 = 𝑦(10.58𝑖𝑛) =
1
8.386 ∗106 𝑙𝑏∙𝑖𝑛2 [
600𝑙𝑏
6
(10.58𝑖𝑛)3
− 33600𝑙𝑏 ∙ 𝑖𝑛2
(10.58𝑖𝑛)]
𝑦 𝑚𝑎𝑥 = −.02827 𝑖𝑛

7. Page 6 of 8
Predictions:
Maximum Load:
𝑃𝑚𝑎𝑥 = (𝑆. 𝐹. ) 𝑚𝑖𝑛 ∗ 𝑃 = 2.390(1500𝑙𝑏) = 3585 𝑙𝑏
Strength-to-Weight Ratio:
𝑆. 𝑊.=
𝑃 𝑚𝑎𝑥
𝑊
𝜌 = 0.0220 𝑙𝑏/𝑖𝑛3
(𝑓𝑟𝑜𝑚 𝑀𝑎𝑡𝑤𝑒𝑏)
𝑉 = (4𝑖𝑛)(2𝑖𝑛)(23𝑖𝑛) − (3.5𝑖𝑛)(1.5𝑖𝑛)(23𝑖𝑛) = 63.25 𝑖𝑛3
𝑊 = 𝜌𝑉 = (0.0220𝑙𝑏/𝑖𝑛3)(63.25𝑖𝑛3) = 1.392 𝑙𝑏
𝑆. 𝑊.=
3585𝑙𝑏
1.392𝑙𝑏
= 2582.6
Failure Type and Location:
The glue will shear in the region to the right of the applied force, where the
internal shear force is greatest.

8. Page 7 of 8
Test Results:

9. Page 8 of 8
Discussion of Results:
Our beam failed at 1783 pounds, much lower than our predicted maximum. However, it
failed in a way that we did not anticipate and one that is very difficult to predict. The top plate of
the beam developed a flange crack, which forms as a result of bending in that plate. Again, a
flange crack is very difficult to predict and was not one of the failure types we took into account
while designing the beam.
Conclusions and Recommendations:
Although our beam did not make it to our predicted maximum, it did fail within the 1000-
2000 pound range that was the target. The only failure type we experienced was the flange
crack; without it, the beam could have held more weight and gotten closer to our predictions.
To improve our design in the future, our cross section could be changed to a more stable
configuration to reduce the chances of a flange crack occurring. One possible design would be a
combination of a box beam and an I-beam, such as an I-beam with two webs, separated by a gap.
The rest of the beam held up quite well, so eliminating that failure would significantly increase
the maximum strength of the beam, to be more in line with our predictions.
Crack visible on both sides of the
roller for the applied force