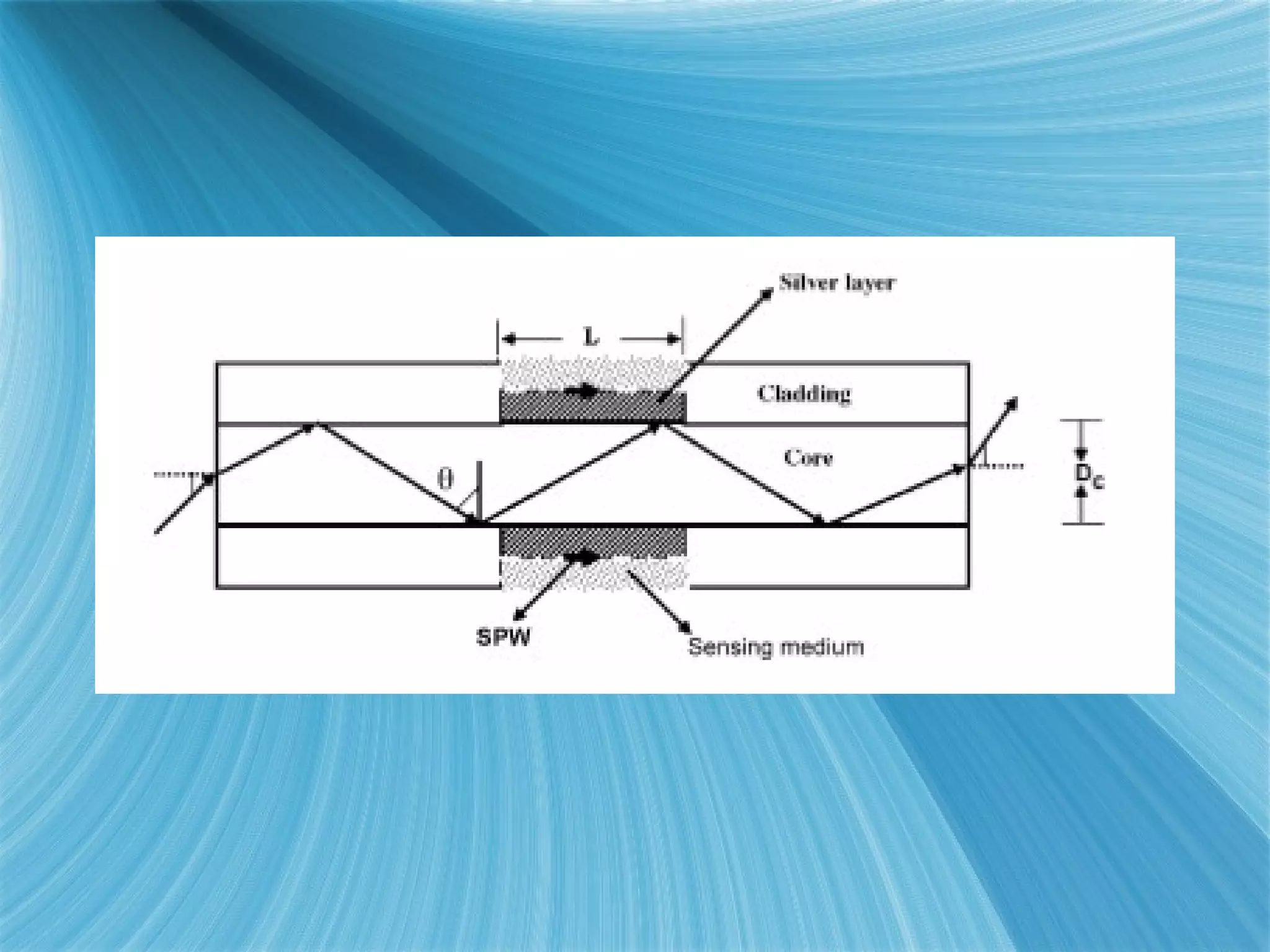
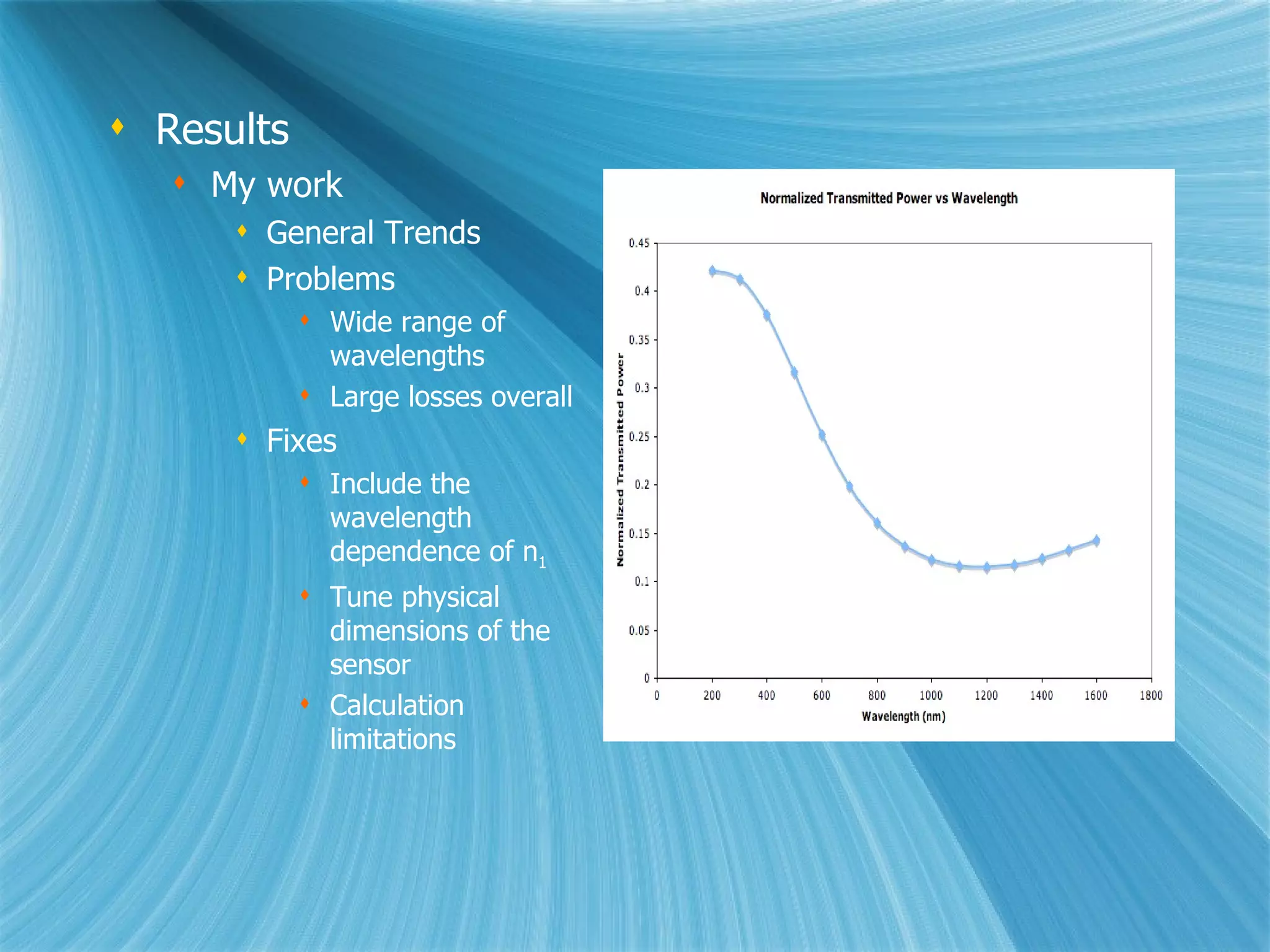
The document proposes using surface plasmon excitation at the boundary between an optical fiber and an unknown medium for chemical sensing applications. Power transmitted through the fiber is reduced by plasmon excitation, with the wavelength-dependent loss revealing the permittivity of the unknown medium. By matching boundary conditions, a thin metal film coated on the fiber core supports plasmon excitation for transverse magnetic (TM) modes when submerged in the sensing medium, but not for transverse electric (TE) modes. This fiber sensor could enable portable, lightweight detection of various chemicals in applications like water quality monitoring and precision agriculture.

1. Plasmonic Excitation At The Boundary Between An Optical Fiber & An Unknown Medium For Sensing Applications Joshua Bradford Physics 504-Fall 2009

2. Chemical Sensors Needs Determination of unknowns Determination of concentrations of knowns Traditional Methods and Limitations Spectrometry to look at florescence or Raman shift Mass Spectrometry to look at constituent elements Bulky and Expensive

5. Fiber Method The cladding of a fiber is chemically stripped. Then the exposed core is coated with a then metal film. Finally, the prepared fiber is submerged in the sensing medium. Power of TM modes sent through the fiber get reduced by excitation of plasmons. Matching of boundary conditions across the metal film for the excitation depend on all 3 constituent media. The wavelength dependent loss tells you the permittivity of the unknown.

6. Plasmonics From the Drude model of electron gases, a metal’s entire free electron sea can be displaced w.r.t. the ion core background by electromagnetic radiation. The quantization of this displacement is known as a plasmon. Surface Plasmon Polaritons (SPP's) are transverse electron density waves that occur along the interface between a metal and a dielectric. SPP’s have momentum along the interface and decay exponentially into both materials away from the boundary.

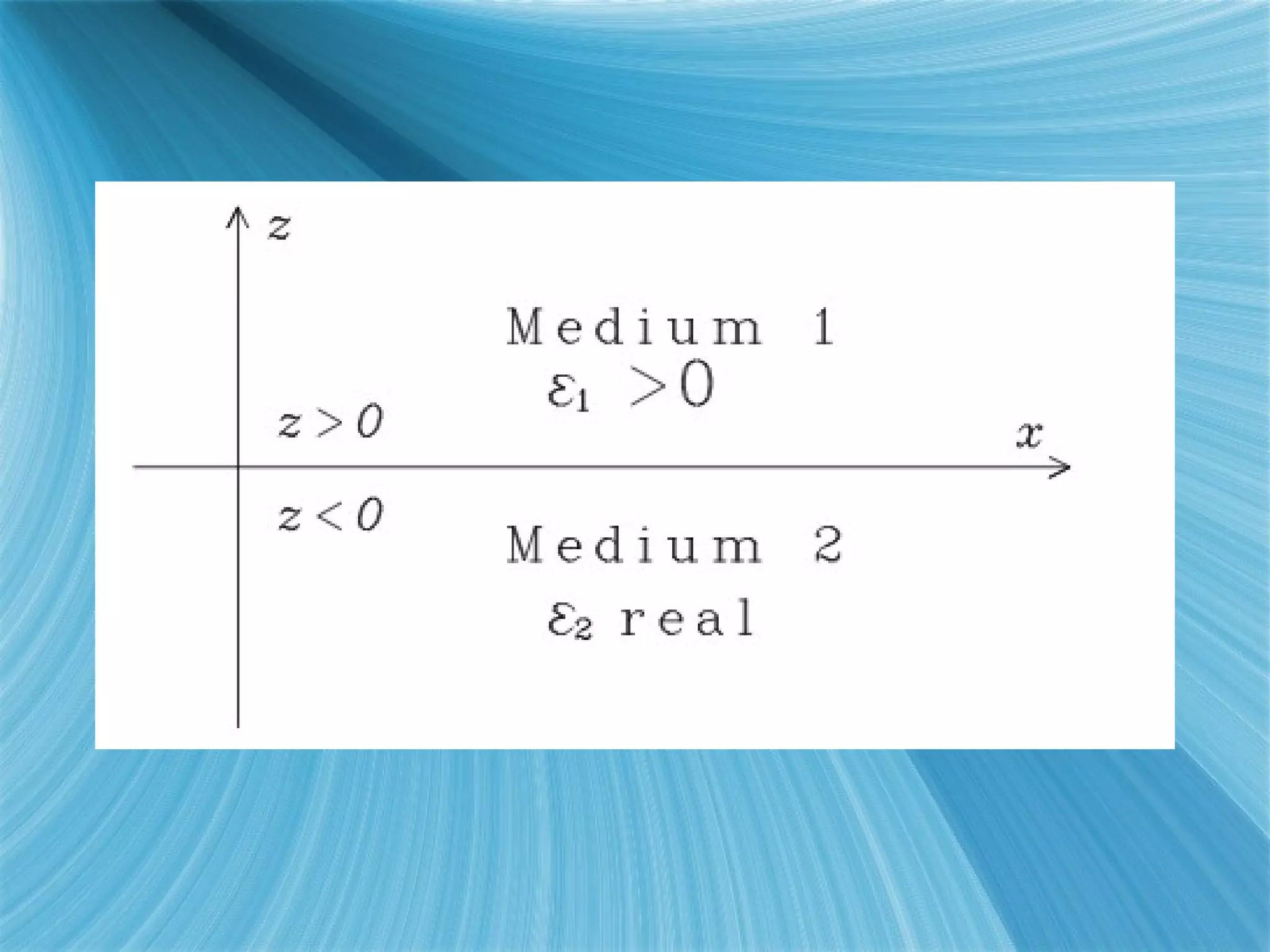
8. For TM mode excitation Matching boundary conditions [3]  1 *(k 2 -  2 *(  2 /c 2 )) 1/2 = -  2 *(k 2 -  1 *(  2 /c 2 )) 1/2  2 < 0 & -  2 >  1 Dispersion Relation  2 =(c*k) 2 *(1/  1 +1/  2 ) For TE mode excitation Matching boundary conditions requires a negative permeability. Not possible so the plasmon mode is not supported.

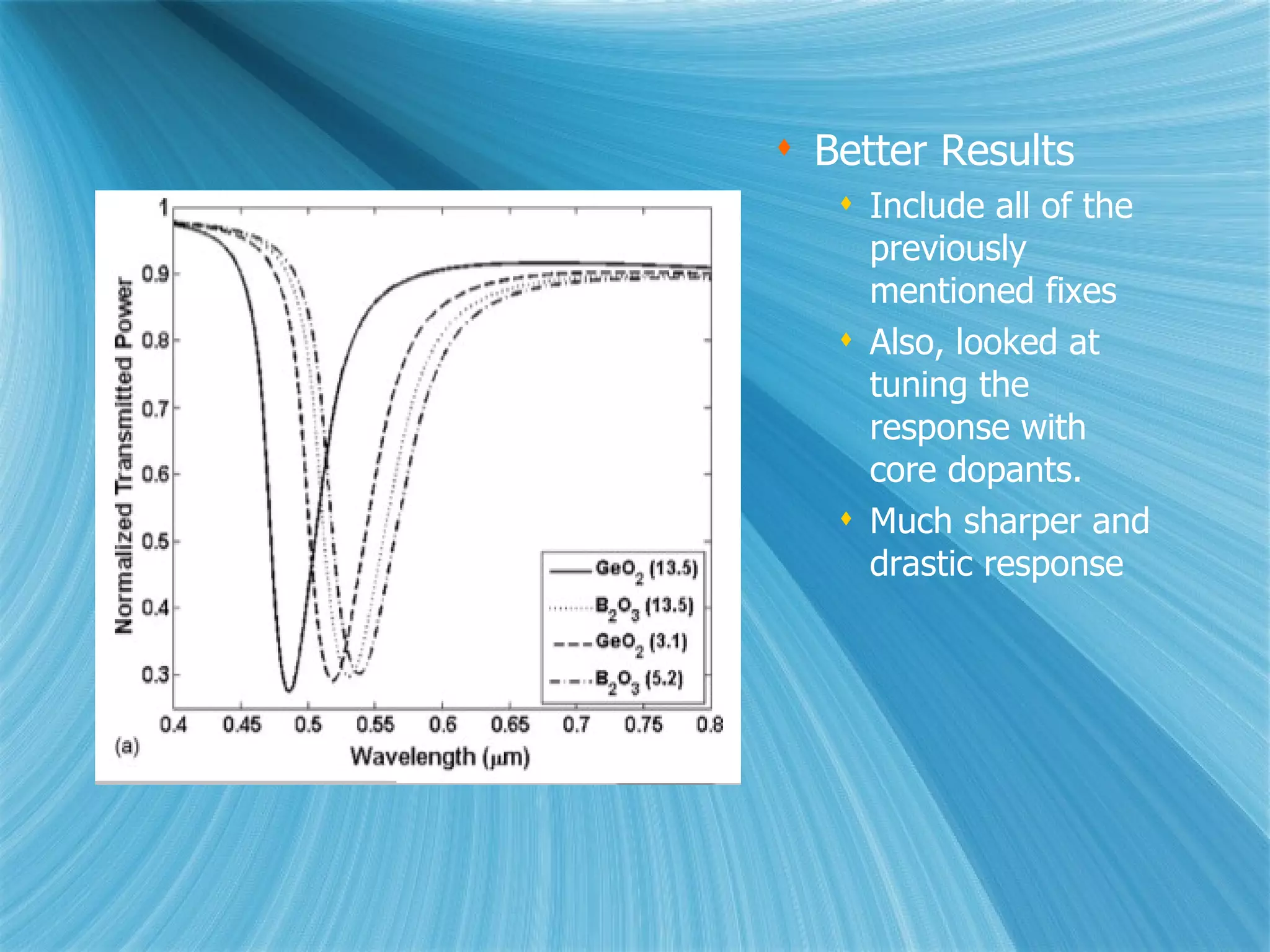
9. Math Matrix method for stacked layers [4] The radiation through the k th component is multiplied by the the transfer matrix {{cos  k (- i *sin  k )/q k }{cos  k - i *sin  k *q k }}  k = ((2*  *d k )/  )* Sqrt[  k -n 1 2 *sin 2  ] q k = Sqrt[  k -n 1 2 *sin 2  ]/  k Multiply the transfer matrices for all components to obtain M t [1] Then the Fresnel reflection amplitude is r p =((M 11 +M 12 *q N )*q 1 -(M 21 +M 22 *q N ))/ ((M 11 +M 12 *q N )*q 1 +(M 21 +M 22 *q N )) Reflection coefficient is R p = abs(r p ) 2

10. Total Reflection coefficient is R p Num(  ) Num(  ) = L/(D core *tan  ) Power Transmitted through the sensor dP/d  = A*(n 1 2 *sin  *cos  )/(1- n 1 2 *cos 2  ) dP’ =R p Num(  ) *dP Then the normalized power transmitted through the sensor is (∫dP’ ) /(∫dP ) such that the limits of integration are from  critical to  /2. At certain wavelengths different sensing materials will support plasmonic excitation and the normalized through power will drop significantly.

11. Results My work General Trends Problems Wide range of wavelengths Large losses overall Fixes Include the wavelength dependence of n 1 Tune physical dimensions of the sensor Calculation limitations

12. Better Results Include all of the previously mentioned fixes Also, looked at tuning the response with core dopants. Much sharper and drastic response

13. Uses [2] Portable sensor for monitoring water quality–nutrients, pesticides, pathogens, heavy metals, sediment,… Portable sensor for inspecting biofuel composition(e.g. blend ratio between biofuel and petroleum fuel), impurities,… Fixed sensor for detecting biofuel-petroleum fuel blend ratio as a feedback signal to automatically adjust fuel injection or ignition timing to maximize fuel efficiency while reducing emissions,… Portable sensor for monitoring air quality- particulate matter (PM), diesel exhaust, and volatile organic compounds (VOCs), … Quick measurement of soil nutrient levels for precision agriculture,…

14. Pros Lightweight & Small Robust Analysis light never travels through the sensing media Cons Cost? Very involved math for extrapolation of desired information about the sample

15. Questions…?

16. References [1] Fundamentals of Photonics. Saleh, Teich. 2nd ed. 2007. John Wiley and Sons, Inc. [2] A Real-time Permittivity Sensor for Simultaneous Measurement of Multiple Water-Quality Parameters. Zhang, Tang, Shultz, Barnes. 2009. Biological and Agricultural Engineering, Kansas State University. [3] Surface Plasmon Resonance in a Thin Metal Film. Stoltenberg, Pengra. 2008. Washington University. [4] Effect of fiber core dopant concentration on the performance of surface plasmon resonance-based fiber optic sensor. Badenes, Jra. Sensors and Actuators A 150 (2009) 212–217. Elsevier.